| Titel: | Beschreibung und Berechnung einer einfachen, guten Pferdmühle; zulezt von dem Vorzuge derselben vor einer Ochsenmühle. Vom Prof. Dr. Herrmann in München. |
| Autor: | Prof. Dr. Johann Baptist Herrmann [GND] |
| Fundstelle: | Band 4, Jahrgang 1821, Nr. XVIII., S. 161 |
| Download: | XML |
XVIII.
Beschreibung und Berechnung einer einfachen, guten Pferdmühle; zulezt von dem Vorzuge derselben vor einer Ochsenmühle. Vom
Prof. Dr. Herrmann in München.
Mit Abbildungen auf Tab. II.
Herrmann's Beschreibung u. Berechnung einer einfachen, guten Pferdemühle etc.
Ein Pferd von mittlerer Staͤrke kann auf ebenem Boden
zwei Stunden lang eine Last als 175 bis 185 Pfund nach Nuͤrnberger, oder 160
bis 169 Pfund nach Wiener und baierischem Gewichte ziehen. Bei dieser Anstrengung
macht es in 2 Stunden einen Weg von 2400 Pariser, oder 25640 Nuͤrnberger
Schuhen, naͤmlich eine gute deutsche Meile. Diese Angabe wird durch die
Erfahrung bestaͤtiget. (Den siebenten Theil jener Last oder 25 Pfund bringt
ein Mann von mittlerer Starke auf einem guten Wege ebenfalls in 2 Stunden eine Meile
weiter.)
Ob das Pferd diesen Weg in einer geraden Linie, oder in einer solchen
Kruͤmmung, die ihm keinen Schwindel verursacht, zu laufen habe, ist hier
gleichviel. Werden dem Pferde die Augen geblendet, oder gebraucht man ein blindes
Pferd, so wird auch die Bewegung im Kreise auf keine Art nachtheilig.
Was nun bei den Wassermuͤhlen die Geschwindigkeit des Wassers, und die Kraft
seines Stoffes auf das Wasserrad thut, das leistet bei der Pferdemuͤhle die
angegebene Geschwindigkeit und Kraft des Pferdes.
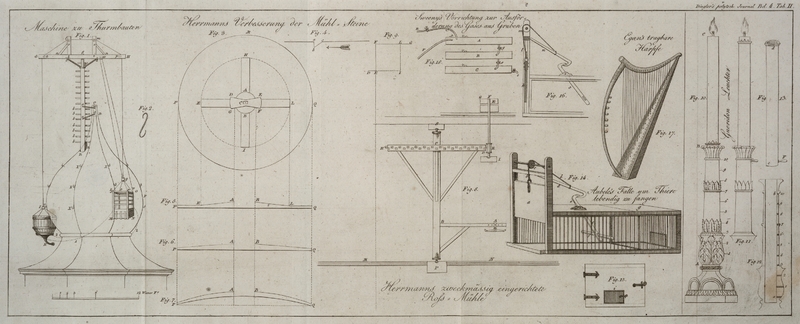
Die wesentliche Einrichtung einer solchen Muͤhle stellt die 8. Figur auf Tab. II. dar. In der Mitte der ebenen, wagerechten
Laufbahn fuͤr das Pferd MN ist ein starker
Stock oder Stein mit
einer eisernen Pfanne, in welcher die untere Achse des Wellbaums PS aufsizt, befestiget. An diesem ist in
gehoͤriger Hoͤhe die Deichsel BA
angebracht. Dieser Hebelarm, an dem das Pferd wirkt, darf von der Mitte des
Wellbaums an nicht weniger, aber auch nicht viel mehr, als 12 Schuhe lang seyn.
– An dem naͤmlichen Wellbaume befindet sich auch in einer Hoͤhe
von etwa 9 Schuhen das Stirnrad DH, welches in das
Getriebe, oder den Trilling E eingreift, der sammt dem
Laufer FG das unten bei I in Mitte des Steeges in einer Pfanne aufsizenden Muͤhleisen IK traͤgt.
Es kommt nun darauf an, welches Verhaͤltniß Rad und Getriebe zu einander haben
sollen, damit der Laufer in einer bestimmten Zeit, z.B. in einer Minute oft genug
umlaufe, und was sein Durchmesser und sein Gewicht seyn muͤsse, wenn das
Pferd mit seiner Kraft und Geschwindigkeit den Widerstand des Getreides bei seinem
Umlaufe uͤberwinden soll. Da beide hier nicht so groß sind, wie bei einer
Wassermuͤhle, so sieht man leicht ein, daß auch weder der Durchmesser, noch
das Gewicht und die Geschwindigkeit des Laufers so groß seyn muͤsse.
Wenn der Laufer beinahe einmal in einer Sekunde, oder 60 mal in einer Minute
herumgeht, so hat er schon eine große und ganz passende Geschwindigkeit. Wir wollen
dieser gemaͤß das Sternrad und den Trilling eintheilen, und sodann durch
Rechnung den Durchmesser und das Gewicht des Laufers suchen, um zu erfahren, ob das
angesezte Verhaͤltniß beizubehalten, oder abzuaͤndern sey.
Da die Anspann des Pferdes 12 Schuhe lang ist, so macht dieses in einem Umgange einen
Weg von 754 Schuhen, naͤmlich den Umkreiß eines Zirkels von 24 Schuhen im
Durchmesser. Dividirt man damit den Weg von 25640 Schuhen, welchen das Pferd in 2
Stunden zuruͤcklegt, so ist der Quotient 340, der uns anzeigt, wie oft das Pferd, und
folglich auch das mit der Welle des Anspanns verbundene Sternrad in 2 Stunden
herumgehe. Es kommen aber auf 1 Stunde oder 60 Minuten 170, und auf 6 Minuten oder
360 Sekunden 17 Umgaͤnge.
Wenn also der Laufer in einer Sekunde beinahe einmal umlaufen soll, so muß dieses bei
17 Umgangen des Sternrades 360 mal, folglich in Einem Umgange desselben fast 21 mal
geschehen. Es muß demnach die Zahl der Triebstaͤbe bei dem Getriebe oder
Trillinge, die man gewoͤhnlich zu 6 annimmt, der 21te Theil von der Zahl der
Zaͤhne des Sternrades seyn; folglich ist diese 6 mal 21, das ist 126.
Es ist aber diese Zahl zur Abtheilung des Rades nicht brauchbar, weil auf den 4ten
Theil desselben 31 1/2 Zaͤhne treffen wuͤrden; wir wollen daher 32
annehmen, und dem Rade 128 Zaͤhne geben. Diese Zahl ist auch wirklich die
beste, und leichteste zur Abtheilung, weil sie sich durch bestaͤndiges
Halbiren bis auf den lezten Zahn vollenden laͤßt. Die Sechserzahl des
Getriebs ist indeß kein Theiler von 128, und es kommt der naͤmliche Triebstab
nicht immer auf den naͤmlichen Zahn des Rades: dieses Wechseln ist aber
vortheilhaft, weil sich nach und nach alle Zaͤhne gegen die
Triebstaͤbe abrichten.
Um einzusehen, wie durch die Veraͤnderung der Anspanne des Pferdes die
Geschwindigkeit des Laufers genau bestimmt, und nach Gutbefinden veraͤndert
werden koͤnne, wollen wir die umgekehrte Rechnung anstellen.
Wenn der Laufer in einer Sekunde einmal umgehen soll, so macht er in 2 Stunden 7200
Umgaͤnge; da nun das Sternrad 128 Zaͤhne, und der Trilling 6
Staͤbe hat, so macht ein Umgang von jenem, folglich auch vom Pferde 128/6
oder 64/3 Umgaͤnge des Laufers. Dividirt man damit 7200, so zeigt der
Quotient 337 1/2 an, daß das Pferd in 2 Stunden eben so oft herumgehen muͤsse. Wird mir
eben diesem Quotient der ganze Weg von 25640 dividirt, so gibt der neue Quotient den
Umkreis von 75,97 Schuhen, welchen das Pferd macht: wird dieser mit 7 multiplizirt,
und mit 22 dividirt, so erhalten wir den Durchmesser dieses Umkreises von 24 Schuhen
und 2 Zoll, folglich die Anspanne von 12 Schuhen 1 Zoll, die von der anfangs
angenommenen nur um 1 Zoll groͤßer ist, und so wollen wir sie auch in der
Folge annehmen.
Von dieser Rechnungsart laͤßt sich auch noch ein anderer vortheilhafter
Gebrauch machen. Man bemerkt, zum Beispiel, daß der Widerstand, welchen das Getreide
dem Laufer entgegensezt, etwas groͤßer sey, als in der Rechnung angenommen
wurde, entweder wegen des groͤßern Gewichts des Laufers, oder wegen der
geringern Kraft des Pferdes; man wird also die Geschwindigkeit des Laufers
vermindern muͤssen. Er soll nun in einer Minute nicht mehr 60 mal, sondern
nur 54 mal, mit Beibehaltung des naͤmlichen Rades und Getriebes umlaufen;
demnach wird er in 2 Stunden 6480 Umgaͤnge vollenden; diese mit 64/3
dividirt, geben 303 3/4 Umgaͤnge des Pferdes; theilt man durch diese die Zahl
25640, so lernt man den Umkreis von 26 Schuhen 10 Zoll, und folglich die Anspann von
13 Schuhen 5 Zoll kennen, wo das Pferd mit Erleichterung seines Ganges eine
groͤßere Last wird uͤberwinden koͤnnen.
Man ersieht hieraus, daß es gut ist, wenn man den Hebelarm, woran das Pferd gespannt
wird, verlaͤngern kann.
Nun wollen wir die Groͤße des Rades und Getriebes berechnen, wenn dieses 6
Staͤbe, und jenes 128 Zaͤhne haben soll. Ein Triebstab ist mehr als
hinlaͤnglich stark, wenn er 2 Zoll oder 24 Linien im Durchmesser hat.
Verhaͤlt sich dieser zum Zwischenraum wie 8 zu 7, so hat lezterer 21 Linien, und beide
zusammen 45 Linien; diese 6 mal genommen geben den Umkreis von 270 Linien durch den
Mittelpunkt der Staͤbe; folglich ist der Durchmesser 85 10/11 oder sehr nahe
an 86 Linien, also der Halbmesser 43.
Der Umkreis des Trillings verhaͤlt sich zum Umkreise des Rades, wie 6 zu 128;
es ist also der Umkreis von lezterem 5760 Linien oder 40 Schuhen, folglich der
Durchmesser 12', 8'', 9 1/2''', oder bis zum Rande der Zaͤhne 12', 9 1/4'',
und der Halbmesser 6', 4'', 6'''.
Ohne Spielraum waͤre die Zahndike = 21''', dem Raume zwischen den
Triebstaͤben; man darf aber wegen des Spielraums fuͤr 7 Linien jedes
mal eine halbe abrechnen, mithin waͤre die Zahndike 19 1/2 Linien, gewiß sehr
stark. Man kann sie auch beliebig nach der eben angestellten Rechnung verkleinern;
das Verhaͤltniß bleibt immer das naͤmliche, und es veraͤndert
die noch uͤbrige Rechnung nicht; doch wenn dabei der Halbmesser des
Sternrades kleiner ist, so waͤchst das Verhaͤltniß der Anspann zu
demselben etwas mehr, als es zwischen dem Halbmesser des Trillings und Laufers
abnimmt, und befoͤrdert auf solche Art etwas die wirkende Kraft des
Pferdes.
Ehe wir die Rechnung anstellen, muß der Erfahrungssaz vorausgesezt werden:
daß der Widerstand, welchen das Getreide der Bewegung des Laufers
entgegensezt, beinahe der 35 Theil von dem Gewicht das der Steeg traͤgt,
ist.
Man muß sich aber diesen Widerstand vorstellen, als sey er von der Mitte des Laufers
gesammelt in 2/3 Theilen seines Halbmessers, wo naͤmlich der Mittelpunkt der
Schwere von jedem Ausschnitt des Zirkels sich befindet. Wie dieser Widerstand gegen
das Sternrad wirke, laͤßt sich also erklaͤren: Es sey Fig. 9. DE der halbe Durchmesser des Trillings, und FG der halbe Durchmesser des auf dem
Muͤhleisen FE sizenden Laufers. Bei L in 2/3 von FG sey
dieser Widerstand als eine gegen das Sternrad bei D
wirkende Kraft gesammelt. Man verlaͤngere DE bis in I, wohin die von FG bei L
herabgelassene Senkrechte faͤllt; so ist es eben so viel, als wenn bei dem
Hebel DE dessen Ruhepunkt in E, der Widerstand in I, und
die Kraft des Sternrades in D sich befaͤnde. Es
verhaͤlt sich also diese Kraft zum Widerstand, nach der bekannten Lehre vom
Hebel, wie EI oder FL naͤmlich 2/3 FG zu DE, das ist, wie 2/3 vom Halbmesser des Laufers
zum Halbmesser des Trillings oder Getriebes. Der Widerstand, oder 1/35 des Gewichts
vom Laufer und Muͤhleisen sey = P, und die Kraft
des Sternrades bei D = Q. So
ist Q : P = 2/3 FG = DE, und Q = P × 2FG/3DE. Es muß also der
Werth fuͤr Q bestimmt werden.
Die bereits als richtig angenommene Kraft des Pferdes sey = V, so ebenfalls nach der Theorie des Hebels, dessen ein Arm die Anspann
AB, der Andere der Halbmesser des Sternrades
CD. CD : AB = V : Q. Also ist Q = V × AB/CD, und da man diesen Werth in der vorigen Gleichung
statt Q sezt; V × AB/CD = P × 2FG/3DE. Die Formel ist allgemein, und gehoͤrt auch
fuͤr Wassermuͤhlen, wenn man fuͤr V
die Wirkung des Wassers auf das Rad, und fuͤr die Anspanne den Halbmesser des
Wasserrads sezt.
Diese Rechnung ist jedoch noch unvollkommen, weil dabei nicht die Reibung der Theile
in der Maschine selbst beruͤcksichtiget ist. Das Muͤhleisen in der
Pfanne, der Wellbaum in seinem doppelten Lager, Zahn und Trieb gegen einander machen
der wirkenden Kraft V einen Widerstand, den sie ebenfalls
uͤberwinden muß. Dieser laͤßt sich zwar, wenn das Gewicht vom
Wellbaum, Rade, Muͤhleisen, und Laufer gegeben ist, fuͤr jedes
insbesondere hinlaͤnglich berechnen; es kann dieß aber auf eine leichtere
doppelte Art geschehen. – Die erste ist diese:
Man stelle sich vor, es sei P, der Widerstand bei dem
Laufer, um so viel groͤßer, als die Reibung der gesammten Theile gegen die
Kraft V ausmacht. Diesen zu P kommenden Theil wollen wir
P/n nennen, wo n anzeigt, der wievielste Theil des ganzen Widerstandes
fuͤr die Reibung anzusezen sei, kommt dieses in der vorigen Formel dazu, und
sezt man P + P/n oder
Textformel Bd. 4, S. 167
so wird sie
Textabbildung Bd. 4, S. 167
Es kommt nur darauf an, was man statt n fuͤr eine Zahl
sezen soll. Belidor fand die Zahl 6; daß naͤmlich der Widerstand durch die
Reibung der 6te Theil von P sei: er bemerkt zugleich,
daß es zuviel sei, wenn man ohne Ausnahme, und ohne Ruͤcksicht auf die Lage
und Zahl der Theile, durchaus 1/3 annimmt. Es ist auch 1/6 fuͤr eine wohl
gebaute Pferdemuͤhle schon zu viel, indem hier das geringere Gewicht des
Laufers, welchen doch Belidor mit einem Durchmesser von 5 Schuhen auf 2200 Pfund
nach Pariser Gewicht berechnet, und der aufrecht stehende Wellbaum keine so große
Reibung verursachen. Belidor fand diese bei der Berechnung einer ganz
aͤhnlichen Pferdemuͤhle fast nur 1/9 von der Kraft des Pferds zu 180
Pfund. Daher haben wir folgende zweite Rechnungsart:
Die Kraft, welche das Pferd durch die Meldung verliert, sei = V/n, somit ist die Kraft, die es zur
Ueberwindung des Widerstandes P anwendet
Textabbildung Bd. 4, S. 167
Sezen wir dieses statt V in der
ersten Formel, so erhalten wir
Textabbildung Bd. 4, S. 167
Wir wollen nun beide Formeln auf die hier beschriebene Pferdemuͤhle anwenden,
um zu sehen, wie groß und schwer der Laufer werden soll.
Vorhin haben wir angesezt AB = 12', 1'' = 1740'''.
CD = 6', 4'', 6''' = 918'''. FG ist noch unbestimmt. Indeß koͤnnen wir
annehmen FG = 2' = 288'''. Es wird sich schon
zeigen, ob diese Sezung richtig sei. DE ist = 43.
Zum Ueberfluß soll seyn n = 6. V wird = 175. P wird gesucht. Bei diesen
Zahlen wird aus der ersten Formel
Textabbildung Bd. 4, S. 168
und also
Textabbildung Bd. 4, S. 168
Aus der zweiten Formel:
Textabbildung Bd. 4, S. 168
und
Textabbildung Bd. 4, S. 168
Wir haben also den Widerstand, welchen das Getreide dem Laufer macht, nach beiden
Formeln; wird er mit 35 multiplizirt, so gibt das Produkt das Gewicht des Laufers
sammt dem Muͤhleisen.
Nach der ersten Formel ist 63,674 × 35 = 2228,59 Pfd.
Nach der zweiten wird 61,905 × 35 = 2166,675. Die hier eben nicht bedeutende
Differenz kommt daher, weil es nicht ganz einerlei ist, ob man P groͤßer, oder V
kleiner mache zur Abrechnung der Friktion; dem; im erstem Falle wirkt sie vom
laͤngern Hebelarm des Laufers gegen das Pferd, im zweiten erstreckt sie sich
nicht mehr dahin.
Der Theorie mehr angemessen ist die zweite Formel. Wir behalten also P = 2167 gerade
aus; auf einige Pfunde kommt es hier ohnehin nicht an.
Das Gewicht des Muͤhleisens darf hier nicht uͤber 150 Pfund angesezt
werden. Diese von 2167 abgezogen, lassen fuͤr das Gewicht des Laufers 2017
Pfund uͤbrig.
Nun ist zu untersuchen, wie groß der Laufer seyn soll, und ob man nicht den
angenommenen Durchmesser von 4 Schuhen groͤßer oder kleiner machen
muͤsse. Die Sache haͤngt von der Gattung des Muͤhlsteins, und
seiner eigenthuͤmlichen Schwere ab. Ich nehme hier den Wendelsteiner Muͤhlstein an, wovon der Kubikschuh 142 Pfund wiegt.
Dividirt man damit das Gewicht von 2017 Pfd., so zeigt der Quotient den
koͤrperlichen Inhalt des Steins von 14,2 Kubikschuhen an.
Hat der Laufer 4 Schuhe im Durchmesser, so hat die Zirkelflaͤche desselben
12,566 Quadratschuhe; hievon muß die mittlere Oeffnung von 6 Zoll abgezogen werden,
wovon die Flaͤche = 0,196: es bleiben nun fuͤr die wahre
Flaͤche des Laufers 12,37 Quadratschuhe. Dividirt man damit den
koͤrperlichen Inhalt, so gibt der Quotient die Hoͤhe von 1,148 Schuhe
= 1', 1'', 9'''. Diese ist nicht zu groß, und man kann dem Laufer ganz richtig einen
Durchmesser von 4 Schuhen geben. – Wir wollen ihn aber auch nach der ersten
Formel berechnen, nach welcher mit Abzug von 150 Pfund fuͤr das
Muͤhleisen sein Gewicht 2078 Pfund ist. Dividirt man diese mit 142, so
erhaͤlt man fuͤr dieses Gewicht 14,56, welche durch die weitere
Theilung mit 12,37 fuͤr die Hoͤhe des Laufers 1,177 Schuhe = 1', 2'',
1 1/2''' geben, die von der vorigen nur um 3 1/2 Linien unterschieden ist. Man sieht
also, daß es keinen Unterschied macht, ob man die Untersuchung aus der ersten oder
zweiten Formel anstellet. Belidor fand bei seiner Rechnung fuͤr eine
Pferdemuͤhle das Gewicht des Laufers 2200 Pariser, oder 2112
Nuͤrnberger Pfund, und da er dem Laufer einen Durchmesser von 5 Schuhen gibt,
erhaͤlt er doch eine Hoͤhe von 1 1/2 Pariser Schuhen. Die Ursache des
groͤßern Durchmessers bei diesem liegt in dem geringem Gewichte des Steins,
von welchem nach seiner Angabe der Pariser Kubikschuh nur 110 Pfund wiegt. Man sieht
hieraus, wie nothwendig es sei, bei Berechnung des Laufers auf die
eigenthuͤmliche Schwere des Steins, aus welchem derselbe gemacht ist,
Ruͤcksicht zu nehmen.
Nach dieser Beschreibung und Berechnung einer Pferdemuͤhle wollen wir noch die
Wirkung derselben im Verhaͤltnisse zu einer Wassermuͤhle, wie viel
Getreide z.B. in zwei Stunden gemahlen werden koͤnne, besonders als
Rechnungsmuster anfuͤhren.
Fuͤr die Wirkung des Laufers gilt es gleich viel, ob derselbe von der Kraft
des Wassers, oder eines Pferdes in Bewegung gesezt werde: sie haͤngt allein,
im zusammengesezten Verhaͤltnisse, von dem Gewichte sammt dem
Muͤhleisen, dem halben Durchmesser, oder vielmehr von 2/3 desselben, und von
der Geschwindigkeit des Laufers ab. Hier ist dieses Verhaͤltniß 2167 ×
4/3 × 60 = 173360, weil der Laufer in einer Minute 60 mal umlaͤuft.
Nun muß man das Verhaͤltniß von einer andern guten Muͤhle, sammt dem
Getreide wissen, welches etwa in 2 Stunden, oder einer andern bestimmten Zeit in
derselben gemahlen wird.
Ich waͤhle hier jene, welche Belidor
anfuͤhrt und berechnet. Der Laufer hatte 6 Pariser Fuß im Durchmesser, wog
sammt dem Muͤhleisen beinahe 4348 Pfund nach Pariser Gewicht, lief in einer
Minute 53 mal um, und mahlte in 24 Stunden 120 Septiers Getreide. Das Septier gibt
er im Gewichte zu 75 Pfund an. Nach dem Nuͤrnberger Maß und Gewicht sind die
Zahlen FolgendeWarum ich hier das
Nuͤrnberger Maß und Gewicht vor dem bairischen oder einem andern
anseze, davon habe ich den Grund schon bei einer andern Abhandlung
uͤber Verbesserung und Beurtheilung unserer deutschen
Wassermuͤhlen in diesen Blaͤttern angegeben.:
Durchmesser des Laufers 5 Schuh 6 Zoll. Gewicht 4156 Pfund. – Umlaufszahl in
einer Minute 53. – Gewicht des in 24 Stunden gemahlnen Getreides 8640 Pfund,
kommen auf 2 Stunden 720 Pfund. Das zusammengesezte Verhaͤltniß aus 2/3
× 3,25 × 4156 × 53 ist = 477247. Es ist also dieses
Verhaͤltniß zum vorigen, wie 720 zur Zahl der Pfunde, welche die
Pferdemuͤhle in 2 Stunden mahlet; naͤmlich 477247 : 173360 = 720 :
261,5. Es sollte also die Pferdemuͤhle in 2 Stunden 260, in einer 130 Pfund
Getreide mahlen. Diese Zahl moͤchte Manchem zu groß scheinen; denn ein
mittelmaͤßiger Mahlgang, mit einem kleinen Laufer und 180 Umgaͤngen
desselben in einer Minute, mahlt freilich in einer Stunde nicht uͤber 40 bis
50 Pfund Getreide. Belidor hat indeß von franzoͤsischen Muͤhlen mit
Muͤhlsteinen von viel groͤßerem Durchmesser geschrieben, wo das
Getreide schon auf Einem Zuge gemahlen wird, waͤhrend man bei unsern
deutschen Muͤhlen mit so kleinem Laufer mehrere Zuͤge machen muß. Wir
wollen jedoch noch ein anderes Muster einer bei uns gewoͤhnlichen, ganz
mittelmaͤßigen Muͤhle zur Rechnung annehmen.
Der halbe Durchmesser des Laufers habe 1 1/2 Schuhe, oder 2/3 davon 1 Schuh; sein
Gewicht sammt dem des Muͤhleisens 1200 Pfund; der Laufer gehe in einer Minute
180 mal um, und in einer Stunde werden 40 Pfund Getreide gemahlen: so ist das
zusammengesezte Verhaͤltniß bei dieser Muͤhle = 1 × 1200
× 180 = 216000, und wir haben 216000 : 173360 = 40 : 32 Pfund Getreide,
welche in einer solchen Muͤhle in 4 bis 5 Zuͤgen gemahlen
wuͤrden.
Sollte das Getreide nur mit einem Zuge, wie z.B. das Malz zerrissen werden, so
duͤrfte man leicht das Vierfache hievon, also 128 auf eine, und 256 Pfund auf
2 Stunden ansezen.
Die Zahlen sind wohl nicht zu groß, und beweisen, daß eine gute Pferdemuͤhle
zu einer mittelmaͤßigen, gewoͤhnlichen Wassermuͤhle sich
verhalte, wie 32: 40, oder wie 4 zu 5. Doch mit dem Unterschiede, daß durch ein
Pferd die Muͤhle innerhalb 24 Stunden nicht uͤber 8 Stunden im Gange
seyn kann, weil immer nach 2 Stunden das Pferd wieder einige Zeit ausruhen muß.
Wollte man sie bestaͤndig im Gang erhalten, so waͤren 3 Pferde
erfoderlich. Aber auch eine unterschlaͤgige Wassermuͤhle, und noch
mehr eine Flußmuͤhle, steht manches mal im Jahre wegen zu hohen Wasserstandes
still, und ist bei zu niedrigem Wasserstande von geringer Wirkung, waͤhrend
die Pferdemuͤhle stets in einem gleichfoͤrmigen Gange bleibt. Bringt
man dabei noch den oft sehr kostspieligen Wasserbau, und die haͤufigen
Reparationen, welchen solche Muͤhlen unterworfen sind, in Anschlag, so
moͤchte die Behauptung wohl nicht uͤbertrieben seyn: daß eine
Pferdemuͤhle, wenn gleich zu ihrem bestaͤndigen Gange 3 Pferde
gehoͤren, in Vergleichung der Wirkung und der Kosten einer
gewoͤhnlichen Wasser- oder Flußmuͤhle, die gleichfalls nur
einen Mahlgang hat, nicht nachzusezen sey.
Wir haben Uͤberhaupt, so viel mir bekannt ist, noch wenige ganz
zweckmaͤßig gebaute Pferdemuͤhlen. Wo Fluß- und
Quellmuͤhlen nicht mangeln, haͤlt man sie ohnehin fuͤr ganz
entbehrlich. Wird aber, was gewiß sehr vortheilhaft ist, zuweilen eine
Pferdemuͤhle zum Malzbrechen fuͤr eine Brauerei gebauet, so geschieht
dieß gewoͤhnlich auf eine sehr unvollkommene Weise. Man
uͤberlaͤßt die Ausfuͤhrung des Werks meistens einem Zimmermann,
oder auch einem sogenannten Muͤhlarzt, die, ohne gehoͤrige
Ruͤcksicht auf die Kraft und die Geschwindigkeit des Pferdes, sich allein
nach den gewoͤhnlichen fehlerhaften Wassermuͤhlen richten. Der Laufer
muß die festgesezten 3 Schuhe im Durchmesser haben, und dabei in einer Minute, wo nicht
180 mal, doch sehr oft umlaufen; um eine so große Geschwindigkeit zu bewirken, wird
das Werk mit Zaͤhnen oder doppelten Raͤdern uͤbersezt, zuweilen
auch die Anspanne kuͤrzer gemacht. Die Folge davon ist zu schnelle
Ermuͤdung des besten Pferdes, oder die Nothwendigkeit, zwei Pferde
anzuspannen. Ich koͤnnte einige Beispiele von solchen aus Mangel an Theorie
verpfuschten Pferdemuͤhlen nennen.
Zum Schlusse moͤgen hier noch einige vergleichende Bemerkungen uͤber
die Ochsenmuͤhlen und den Vorzug der Pferdemuͤhlen vor jenen stehen.
Bei den Ochsenmuͤhlen geht der Ochse auf einer großen schiefliegenden
Tretscheibe, und bringt solche durch sein relatives Gewicht in Bewegung. Er hat
keine Last zu ziehen, muß aber immer Berg an gehen; damit er nicht zu schnell
ermuͤde, soll der Neigungswinkel nicht uͤber 15 Grade haben. Das
absolute oder ganze Gewicht des Ochsens verhaͤlt sich zum relativen, mit
welchem er das Rad bewegt, wie der Radius zum Sinus des Neigungswinkels, z.B. bei 14
Grad wie 1000: 242, und bei 15 Graden wie 1000: 259.
Sezt man das Gewicht des Ochsen auf 650 Pfund, so iß unter einem Winkel des Tretrades
von 14 Grad sein relatives Gewicht 157 Pfund, also geringer, als die Zugkraft bei
einem Pferde. Es werden aber zu einer solchen Muͤhle selten weniger als 4
Ochsen erfodert; folglich ist die Gewalt oder Kraft derselben bei obigem Winkel =
629 = V bei der Formel fuͤr die
Pferdemuͤhle.
Der Durchmesser der Tretscheibe zu 4 Ochsen, deren zwei neben einander gehen, kann
von der Mitte zwischen beiden nicht unter 26 bis 28 Schuh seyn. Es sind also hier 13
bis 14 Schuh, was vorhin AB die Anspann des
Pferdes war. Der Umkreis fuͤr einen Umgang macht beinahe 85 Schuh. An 3
Ochsenmuͤhlen unter einer Neigung der Tretscheibe von 14 Graden und
daruͤber hat sich gezeigt, daß der immer Berg angehende Ochse in einer Stunde
nicht uͤber 5136 Schuh mache: theilt man diese Zahl mit 85, so ist der
Quotient in gerader Zahl 60. Es geht also die Tretscheibe in einer Minute einmal
um.
Soll der Laufer nur Einen Umgang in einer Sekunde machen, so geht er 60 mal
schneller, als die Tretscheibe. Dieß laͤßt sich aber mit dem darunter
angebrachten Kammrad unmittelbar nicht bewirken. Es muß also der Trilling, den es
umtreibt, mit einem zweiten aufrechten Kammrade verbunden seyn, dessen Zaͤhne
den Trilling fuͤr den Laufer an dem Muͤhleisen in Bewegung bringen,
diese Maschine ist demnach mehr zusammengesezt, und leidet auch groͤßeren
Widerstand durch die Reibung der Theile: n = 6
wuͤrde hier schon zu geringe seyn, man darf es gleich 5 annehmen.
Wenn auch der Kubikschuh vom Steine des Laufers 142 Pfund wiegt, so darf man doch in
der Rechnung annehmen, daß dieser bei 5 Schuhen im Durchmesser habe; dann
wuͤrde sein Gewicht sammt dem Muͤhleisen beinahe 2950 Pfund betragen,
und es wuͤrde P = 84 in gerader Zahl. –
Aus diesen Angaben kann man die Anordnung und Berechnung einer solchen Muͤhle
leicht herstellen.
Man laͤßt, so viel ich weiß, die Ochsen 2 Stunden unausgesezt auf der
Tretscheibe gehen; diese lange Dauer ermuͤdet sie sehr, und sie schwizen und
daͤmpfen stark am Ende der Arbeit. Soll die Muͤhle bei Tage in
bestaͤndigem Gange seyn, so sind hiezu wenigstens 8 Ochsen noͤthig.
Eine solche Muͤhle ist daher nicht wohl anderswo zu errichten, als bei einem
großen Braͤuhause, wo mehrere Ochsen zur Mastung eingestellt sind. Es hat
aber die Erfahrung gezeigt, daß solche Ochsen, die zur Muͤhle verwendet
werden, 4 bis 6 Wochen, ja oft noch laͤnger in der Mastung stehen
muͤssen.
Einige, welche die Nuzbarkeit, ja oft Nothwendigkeit wohl einsehen, daß ein
Braͤuhaus eine eigene Muͤhle zum Malzschroten habe, verwerfen die
Pferdemuͤhle darum, weil dazu wenigstens 2 Pferde noͤthig seyen, die
man zu diesem Zweck erhalten muͤsse, waͤhrend die Ochsen der Mastung
halber schon vorhanden waͤren. Vielleicht aber wuͤrden diese Leute
ihre Meinung andern, wenn sie die Berechnung anstellten, ob 2 Pferde, oder 3 Ochsen
mehr Kosten des Unterhalts erfodern. – Zu einer Ochsenmuͤhle ist auch
ein groͤßeres Gebaͤude noͤthig, das etliche 70 Schuhe in der
Laͤnge und Breite hat; sie kostet uͤberhaupt wohl zwei bis dreimal
mehr als eine Pferdemuͤhle; deshalb gab ich dieser immer den Vorzug vor
jenerIn einem großen
Braͤuhause kann eine Ochsenmuͤhle, durch die ohnehin zur
Mastung aufgestellten Ochsen, ohne weitere Kosten betrieben werden. Die
dadurch entstehenden Vortheile sind in oͤkonomischer Hinsicht von
Wichtigkeit, und jedem Braͤuhausbesizer ist daran gelegen, Mastochsen
zum Malzschroten gebrauchen zu koͤnnen. Daher sollten Mechaniker auf
eine Verbesserung und zweckmaͤßige Einrichtung der
Ochsenmuͤhlen ernstlich Bedacht nehmen. B.. Die
Einrichtung der mir bekannten Ochsenmuͤhlen fand ich auch durchaus
fehlerhaft, besonders wegen der gewoͤhnlichen großen Geschwindigkeit kleiner
Laufer; das Raͤderwerk war so angeordnet, daß der Laufer nach der schon
vorgeschriebenen Art in einer Minute 180 bis 200 mal umlief. Man haͤtte
dafuͤr, mit großem Vortheile, bei einer kleinern Umlaufszahl groͤßere
und schwerere Laufer anbringen koͤnnen, wie man sie aus den fruͤhern
Angaben gar leicht berechnen kann.
Tafeln