| Titel: | Ueber eine neue Einrichtung der Zahn- oder Zapfen-Räder. Von Herrn Jakob White, Maschinisten. |
| Fundstelle: | Band 7, Jahrgang 1822, Nr. XLII., S. 287 |
| Download: | XML |
XLII.
Ueber eine neue Einrichtung der Zahn- oder Zapfen-Räder. Von Herrn Jakob White, Maschinisten.
Aus den Memoirs of the Literary et Philosophical Society of Manchester. Im Repertory of Arts, Manufactures et Agriculture. N. CCXXXVII. Februar 1822. S. 142.Herr White hat auf diese
Erfindung schon im Jahr 1788 ein Patent genommen. A. d. O. Obschon diese
Abhandlung mehr theoretisch als praktisch zu seyn scheint, so glaubten wir doch
unseren Lesern dieselbe nicht vorenthalten zu duͤrfen, um so weniger, als
bei uns in Deutschland, zumal in dem Katholischen, das Studium der Mathematik
theils zu sehr vernachlaͤssigt, theils zu schlecht betrieben wird. An
vielen Lehranstalten sind die Lehrer der Mathematik noch heute zu Tage Leute,
denen es mehr um Verfinsterung der Koͤpfe der Jugend als um Aufhellung
derselben durch Foͤrderung des mathematischen Geistes zu thun ist. So
bewies der Professor der Mathematik des Uebersezers, an einer uͤbrigens
beruͤhmten Universitaͤt, durch a
× b, daß Sonnen- und Mondesfinsterniß
zugleich statt haben koͤnne. Wenn der Herr Professor gelehrt
haͤtte: man soll dieß glauben; so koͤnnte man ihn entschuldigen;
da er es aber bewiesen hat, so laͤßt sich nichts anderes dagegen
bemerken, als daß dieser Professor einer Secte angehoͤrte die einen Ruhm
darein sezte, alles zu beweisen und alles zu laͤugnen. A. d.
Ueb.
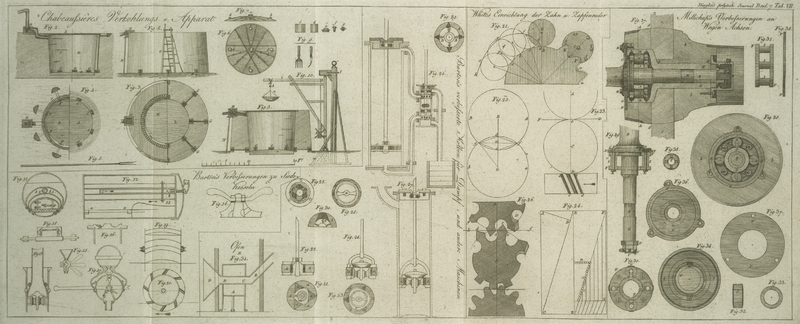
Mit Abbildungen auf Tab. VII.
White über eine neue Einrichtung der Zahn- oder Zapfenräder.
Um sich von der Wichtigkeit des Gegenstandes dieser Abhandlung
zu uͤberzeugen, darf man nur die ungeheuere Anzahl von Zahnraͤdern
bedenken, welche in einer so bevoͤlkere ten und gewerbfleißigen Gegend, wie
jene von Manchester, taͤglich im Umlaufe sind, und den Antheil, welchen diese
Raͤder an der
Menge und an dem Werthe der Erzeugnisse dieser Gegend haben; es wird dann
einleuchtend seyn, daß jede Erfindung, welche dahin abzielt, diese Instrumente zu
vervollkommnen, sey es nun, daß sie dadurch wohlfeiler wuͤrden, oder
laͤnger dauerten, oder daß auch nur ihre Reibung dadurch vermindert
wuͤrde, einen wohlthaͤtigen Einfluß auf das allgemeine Beste haben
muͤsse. Ich hoffe, daß alle diese Zweke in einem mehr oder minder hohen Grade
durch Raͤder, welche nach dem gegenwaͤrtigen neuen Systeme erbaut
sind, erreicht werden koͤnnen.
Ich will mich nicht damit begnuͤgen, diese Behauptungen bloß theoretisch zu
erweisen, sondern ich uͤbersende der Gesellschaft zugleich hier
Raͤder, welche die Eigenschaft besizen, einander in der vollkommensten Stille umzudrehen, indem die Reibung und Abnuzung ihrer
Zaͤhne, wenn ja eine solche an denselben statt hat, so gering ist, daß man
dieselbe gar nicht berechnen kann, und welche, ohne alles Stoßen, bloß durch
staͤten und gleichfoͤrmigen Druk, einander die bekanntlich
groͤßte Geschwindigkeit mitzutheilen vermoͤgen.
Ehe ich zur Beschreibung meiner eigenen Raͤder uͤbergehe, will ich auf
einen auffallenden Fehler der gegenwaͤrtig gebraͤuchlichen
Raͤder aufmerksam machen, ohneobne uͤbrigens bis zu jener Periode zuruͤk hinaufzusteigen, wo
alle mechanischen Werkzeuge und Operationen noch tief unter denjenigen standen,
deren man sich heute zu Tage bedient. Praktische Mechaniker der neueren Zeiten sind,
zufaͤllig, und vorzuͤglich in Großbritannien, auf brauchbarere Formen
und Verhaͤltnisse der Raͤder gekommen, als man ehevor nicht kannte,
waͤhrend die theoretischen Mechaniker, von de la
Hire an, (d.i. seit ungefaͤhr 100 Jahren) einstimmig lehrten, daß
die beste Form der Zaͤhne eines Rades von jener krummen Linie
abhaͤngt, die man Epikykloide nennt, und daß die Zaͤhne, welche an einem geraden
Zahnstoke wirken sollen, von der Form einer einfachen Kykloide abgeleitet werden
muͤssen. Diese Kykloide kann man sich als eine krumme denken, welche von der
Bahn gebildet wird, die der Nagel an dem Umfange eines Wagenrades waͤhrend
der Umdrehung dieses Rades, oder von dem Augenblike, wo dieser Nagel den Boden
verlaͤßt, bis zu dem Augenblike, wo er wieder auf denselben
zuruͤkkehrt, durchlaͤuft: die Epikykloide ist eine Krumme, welche von
der Bahne eines Nagels in dem Umfange eines Rades gebildet wird, welches (ohne zu
Schleifen) uͤber den Umfang eines anderen Rades wegrollt.
Es sey AB in Fig. 21. Tab. VII. ein
Theil des Umfanges eines Rades ABF, auf welches
Zaͤhne aufgesezt werden sollen, die so gebildet sind, daß sie in dem Rade C eine gleichfoͤrmige Bewegung erzeugen, wenn die
Bewegung des Rades ABF gleichfalls
gleichfoͤrmig ist. Man lasse ferner diese so gebildeten Zaͤhne auf die
unbestimmt kleinen Stifte r, i, t, welche in die Flache
des Rades C nahe an dem Umfange desselben eingelassen
sind, einwirken. Um den Zaͤhnen des Rades ABF (nach der gegenwaͤrtig herrschenden Methode) eine geeignete
Form zu geben, befestigt man einen Griffel oder Pinsel an dem Umfange eines Kreises
D, welcher dem Rade C
gleich ist, und legt ein Papier hinter beide Kreise, auf welchem durch Umdrehen des
Kreises D auf AB die
Epikykloide d, e, f, g, s, h gezeichnet werden wird,
deren Basis, wie man sagt, ABF ist, und deren
Erzeugungskreis D ist. So ist also das Rad, welchem die
Zaͤhne angehoͤren sollen, die Basis der Krummen, und das Rad, auf
welches eingewirkt werden soll, ist der Erzeugungskreis. Man muß jedoch bemerken,
daß diese Raͤder in dieser Beschreibung nicht nach ihrem aͤußersten
Durchmesser betrachtet werden, sondern in einer solchen Entfernung von ihrem
Umfange, daß die Zaͤhne gehoͤrig eingreifen koͤnnen; oder, wie Hr. Camus sagt, wo die
urspruͤnglichen Kreise der Raͤder (les cercles
primitifs) einander beruͤhren, d.h. in unserer (englischen)
Landessprache in der Eingriffs-Linie (pitch-line).
Da nun die Mathematiker laͤngst erwiesen haben, daß Zaͤhne, welche auf
obige Weise gebildet sind, den Raͤdern, vorausgesezt, daß die Stifte r, i, t etc. unbestimmbar klein sind, eine
gleichfoͤrmige Bewegung ertheilen, so ist es nicht noͤthig, bei diesem
Punkte noch laͤnger zu verweilen.
In dieser Hinsicht waͤre man also mit der Theorie im Reinen. Allein in der
Praxis muͤssen die Stifte r, i, t etc., welche in
der Theorie unbestimmbar klein angenommen werden, doch auch Staͤrke besizen,
und folglich einen bedeutenden Durchmesser haben, wie sie
in 1, und 2, dargestellt sind. Wir muͤssen daher von der Flaͤche der
Krummen eine Breite, wie v und n = dem halben Durchmesser der Stifte wegnehmen, und dann wird, wie zuvor,
wieder gleichfoͤrmige Bewegung statt haben. Die Mathematiker wissen aber, daß
eine auf diese Art veraͤnderte Krumme nicht mehr in aller Strenge eine
Epikykloide genannt werden kann, und daher sagte ich oben, daß die Zaͤhne der
Raͤder, welche eine gleichfoͤrmige Bewegung erzeugen sollen, von
dieser Krummen abhaͤngen oder abgeleitet werden muͤssen: denn, waͤre die
krumme Linie der Zaͤhne eine aͤchte Epikykloide, so wuͤrde, so
bald die Stifte dik sind, die Bewegung nicht mehr gleichfoͤrmig seyn.
Ich uͤbergehe hier absichtlich mehrere interessante Umstaͤnde bei der
Anwendung dieser schoͤnen Krummen auf die Radbewegung, und ich gebe zu, daß
diese Krumme im Stande ist gleichfoͤrmige Bewegung zu erzeugen, wenn die
Zaͤhne der gewoͤhnlichen Raͤderwerke nach dieser Form gebaut
sind. Allein gerade darin liegt das große Ungluͤk: – abgesehen von der
Schwierigkeit die Zaͤhne nach dieser rein theoretischen Form zu bilden
(was selten versucht wird) kann diese Form auch nicht lang
fortbestehen: und daher kommt es, daß die besten, die stillsten
Raͤder endlich fehlerhaft werden, zu klappern anfangen, die Maschine
verderben, und sie vorzuͤglich zu feineren Operationen untauglich machen.
Die Ursache dieses fortschreitenden Verderbens kann auf folgende Weise
erklaͤrt werden: wir sehen, um wieder auf die 21. Fig.
zuruͤkzukommen, die Basis der Krummen AB in
die gleichen Theile ab, bc und cd
getheilt, und wenn wir den Gang des Erzeugungskreises D
von dem Ursprunge der Krummen bei d bis zur ersten
Abtheilung an der Basis, c, betrachten, so finden wir
nicht mehr als erst den kleinen Theil de der
Krummen entwikelt, waͤhrend ein zweiter gleich großer Schritt des
Erzeugungskreises, cb, die Krumme von e bis f, durch eine weit
groͤßere Streke als bei dem ersten Schritte, weiter fuͤhrt; ein
dritter, gleich großer, Schritt ab wird die Krumme
von f bis g ausdehnen,
wieder weiter als bei dem vorigen Schritte, und so werden alle die folgenden
Entwikelungen der Krummen immer groͤßer werden, bis diese ihren Scheitelpunkt
erreicht hat. Nun korrespondiren aber alle diese Theile mit gleichen Umdrehungen des
Rades, naͤmlich mit den gleichen Theilen ab, bc und cd der Basis und mit gleichen Umdrehungen des erzeugenden Kreises.
Nothwendig muͤssen daher die Theile sg, gf der epikykloidischen Zaͤhne
fruͤher abgenuͤzt werden, als die Theile fe und ed, welche, wenn auch der Druk auf sie derselbe waͤre, mit so viel weniger
Geschwindigkeit gerieben werden, als sie kleiner sind als die anderen. Allein der
Druk ist nicht derselbe. Denn die Linie ag ist die
Richtungslinie, in welcher der Druk der Krummen auf den Punkt g wirkt, und die Linie pq ist die
Laͤnge des Hebelarmes, auf welchen dieser Druk wirkt, um den Erzeugungskreis
um seine Achse zu
drehen, die man sich jezt als feststehend denkt. Da aber die drehende Kraft oder die
Kraft bei dem Umdrehen der Raͤder als gleichfoͤrmig angenommen wird,
so muß der Druk bei g sich umgekehrt wie pq verhalten; d.i. umgekehrt wie der Cosinus des
halben Rotations-Winkels des Erzeugungs-Kreises; er muß also bei s, wo die Krumme ihren Scheitelpunkt erreicht und dieser
Kreis seine halbe Umdrehung vollendet hat, unendlich seyn.
Es ist also klar, daß, abgesehen von den Wirkungen des Stoßes, das Ende eines Epikykloidal-Zahnes sich fruͤher
abnuͤzen muß als jeder andere naͤher an der Basis desselben gelegene
Theil (und wenn dieß hier so der Fall ist, so darf man annehmen, daß es weit mehr
noch bei Zaͤhnen von anderer Form eben so seyn wird), und daß, wenn also
seine Form sich auf diese Weise geaͤndert hat, der Vortheil den er
gewaͤhrt, aufhoͤren muß, weil nichts in der Folge mehr waͤhrend
das Rad fort arbeitet, in Stande ist die vorige Form wieder herzustellen, oder dem
immer zunehmenden Uebel abzuhelfen.
Nachdem ich nun einen großen Fehler an dem gewoͤhnlichen
Raͤder-Systeme dargethan habe, will ich die Grundsaͤze des
neuen Systemes entwikeln, welches man aus folgenden drei Saͤzen einsehen
wird:
1. Die Wirkung eines Rades nach der neuen Art auf ein anderes, in welches dasselbe
eingreift, oder mit welchem es sich dreht, ist in jedem Augenblike der Umdrehung des
Rades dieselbe, so daß die moͤglich kleinste Bewegung des Umfanges des einen
eine vollkommen gleiche und aͤhnliche Bewegung in dem anderen erzeugt.
2. Es gibt bloß zwei Punkte, einen in jedem Rade, welche sich nothwendig gleichzeitig
wechselweise beruͤhren, und ihr Beruͤhrungspunkt wird stets
unbestimmbar nahe an jener Ebene liegen, welche durch die beiden Achsen der
Raͤder laͤuft, wenn die Durchmesser der lezteren an dem Nuz- oder
Drukpunkte in genauem Verhaͤltnisse ihrer respektiven Anzahl der
Zaͤhne stehen: in diesem Falle wird keine merkliche Reibung zwischen den
Beruͤhrungspunkten statt haben.
3. In Folge der oben erwaͤhnten Eigenschaften wird weder die Epikykloidal noch
irgend eine andere Form der Zaͤhne ausschließlich mehr noͤthig seyn,
sondern es koͤnnen mehrere verschiedene Formen ohne alle Stoͤrung des
Grundsazes der gleichfoͤrmigen Bewegung angewendet werden.
Um den ersten dieser Saͤze zu beweisen, muß ich eine Bemerkung des Hrn.
Camus uͤber diesen
Gegenstand aus dem 3. Theil S. 306. seiner Mechanik vorausschiken, wo er sagt:
„wenn alle Raͤder unendlich kleine Zaͤhne haben
koͤnnten, so wuͤrde ihr Eingreifen, das man dann als bloße
Beruͤhrung betrachten koͤnnte, die erforderliche Eigenschaft
besizen (d.h., gleichfoͤrmig zu wirken) indem wir gesehen haben, daß ein
Rad und ein Triebstok dieselbe Tangential-Kraft besizt, wenn die Bewegung
des einen dem anderen durch ein unendlich kleines Eindringen der Theilchen ihrer
respektiven Umfange mitgetheilt wird.“
Man nehme nun an, daß auf der cylindrischen Oberflaͤche eines Spornrades Bc, Fig. 23., wir schiefe
oder vielmehr schraubenfoͤrmige Zaͤhne
einschneiden, von welchen in ac und bd zwei dargestellt, und so gegen die
Flaͤche des Rades geneigt sind, daß das Ende c
des Zahnes ac nicht uͤber die
Flaͤche der Achsen ABc reicht, bis nicht
das Ende b des anderen Zahnes bd dieselbe erreicht hat, so wird dieses Rad der
Idee nach in eine unendliche Anzahl von Zaͤhnen getheilt seyn, oder
wenigstens in eine groͤßere Anzahl, als die Zahl der Theile der Materie,
welche sich in einer Kreislinie von dem Umfange des Rades befindet. Denn man denke
sich die Oberflaͤche eines aͤhnlichen, aber laͤngeren,
Cylinders von demselben abgezogen, und auf der Flaͤche
ABCE, Fig. 24., ausgebreitet,
wo die vorige schiefe Linie der Hypothenuse BC des
rechtwinkeligen Dreiekes CAB wird, und alle
Zaͤhne des gegebenen Rades darstellt nach der Skizze EG am Grunde der Figur. Hier sind die Linien AB und CE gleich
dem Umfange der Basis des Cylinders, und AC und
BE gleich seiner Laͤnge; und wenn
zwischen A und B eine Anzahl
von Theilen der Materie = m, und zwischen A und C eine Anzahl solcher
Theile = n vorhanden ist, so wird die ganze
Oberflaͤche ABCE von diesen Theilen m, n, oder das Produkt von m
und n enthalten; die Linie BC wird aber, einem bekannten Lehrsaze zu Folge, eine Zahl =
√(m² + n) enthalten; woraus erhaͤllt, daß die Linie BC nothwendig laͤnger ist, als AB, und folglich mehr Theilchen der Materie in
sich begreiftEs ist kaum
noͤthig zu bemerken, daß, was immer von dem ganzen Dreieke CAB, Fig. 24. gilt,
auch von jedem aͤhnlichen Theile desselben wahr ist, und sey er auch
noch so klein. Nehmen wir daher an, daß die Hypothenuse BC wieder auf dem Cylinder aufgerollt
wird, von welchem wir sie abgestreift dachten, so wird der wirkende Theil
wirklich sehr klein seyn, aber immer auf die hier beschriebene Weise wirken,
und dem Rade, auf welches er wirkt, und seiner Achse genau im
Verhaͤltnisse der hier erwaͤhnten Groͤße eine gewisse
Tendenz mittheilen. A. d. O..
Es ist uͤberdieß offenbar, daß der Unterschied zwischen den Linien BC und AB von
dem Winkel ACB abhaͤngt, der von bedeutend
verschiedener Weite gewaͤhlt werden kann. Zum gewoͤhnlichen Gebrauche
habe ich jedoch einen Winkel von 15° gewaͤhlt, welchen ich jezt als
Basis der folgenden Berechnungen annehmen will. Die Tangente von 15° ist,
nach den Tafeln, in runden Zahlen 268, wo der Radius 1000 ist; man soll nun die Zahl
der Theile in der schiefen Linie BC finden, wenn
die Linie AB irgend eine andere Zahl t enthaͤlt.
Aus der Geometrie ist BC (x)
= √(r² + t²) = √(1000² + 268²) = 1035
ungefaͤhr; und diese lezte Zahl verhaͤlt sich zu 265, wie die Zahl der
Theilchen in der schiefen Linie BC zu der Zahl der
in dem Umfange AB der Basis des Cylinders
enthaltenen. Hieraus erhellt, daß ein Rad, welches in Zaͤhne von dieser Form
eingeschnitten ist, in der Idee ungefaͤhr viermal so viel Zaͤhne
enthaͤlt, als ein Rad von gleichem Durchmesser, aber unbestimmt duͤnn,
enthalten wuͤrde. Dieses Verhaͤltniß ließe sich noch
vergroͤßern, wenn man einen kleineren Winkel annaͤhme.
So waͤre nun, wie ich glaube, erwiesen, daß die Wirkung eines Rades dieser Art
auf ein anderes, in welches dasselbe eingreift, in Hinsicht auf Schnelligkeit
vollkommen gleichfoͤrmig ist, und daher ist es auch erwiesen, daß eben dieß
von der mitgetheilten Staͤrke gilt.
Ehe ich zu dem zweiten Saze uͤbergehe, muß ich vielleicht einigen
Einwuͤrfen begegnen, welche gegen dieses System von Raͤdern gemacht
wurden, und die vielleicht einigen Lesern bereits selbst aufgefallen sind. Man hat,
z.B. behauptet, daß die Reibung dieser Zaͤhne
durch ihre Neigung gegen die Ebene des Rades vermehrt wird; ich darf aber wohl
annehmen, daß ich bewiesen habe, daß es gerade diese schiefe Stellung, verbunden mit
der gaͤnzlichen Abwesenheit einer Bewegung nach der Richtung der Achsen ist,
welche diese Reibung gaͤnzlich aufhebt, statt daß
sie dieselbe erzeugte. Ich gestehe indessen, daß der Druk auf die Beruͤhrungspunkte groͤßer ist
als er es auf Zaͤhne, die mit der Achse der Raͤder parallel laufen,
nicht seyn wuͤrde, und ich gebe ferner zu, daß dieser Druk strebt die
Raͤder in der Richtung ihrer Achse aus ihrer Stelle zu schieben (außer wenn der Zahn zwei
entgegengesezte Neigungen hat, wodurch dieses Streben aufgehoben wird). Wir wollen
aber diese Gegenwirkung uns als vernachlaͤssigt denken, und die Wichtigkeit
dieser Einwuͤrfe pruͤfen. Was nun zuvoͤrderst den Druk auf den
Punkt D in der Linie BC (welche den in Frage stehenden schiefen Zahn ausdruͤkt)
verglichen mit jenem auf die Linie BE betrifft,
(welche einen Zahn eines gewoͤhnlichen Rades darstellt) so ziehe man die
Linie AD senkrecht auf BC. Wenn der Punkt D
frey uͤber die Linie BC hingleiten kann
(und dieß ist die guͤnstigste Annahme fuͤr die Gegner) so wird sein
Druk senkrecht auf diese Linie geschehen; und wenn der Punkt A sich von A nach B bewegt, so wird der Punkt D, der in
demselben Augenblike den Punkt A verlaͤßt und
sich in der Richtung AD bewegt, waͤhrend
derselben Zeit nur nach D gelangen, indem seine Bewegung
in dem Verhaͤltnisse von AB zu AD langsamer als jene von A war; daher ist, nach dem Grundsaze der virtualen Geschwindigkeiten, sein
Druk auf BC zu jenem auf AC, wie die besagten Linien AB zu DA.
Um diese Druke in Zahlen darzustellen, wird, nach obigen Daten, AC = 1000, AB =
263, BC = 1035, und aus der Aehnlichkeit der
Dreieke BAC, BDA, wird BC : AC : : AB : AD =
268000/1035 = 259 ungefaͤhr. Der Druk auf BC verhaͤlt sich also zu jenem auf AC wie 268 zu 259, oder wie 1035 : 1000.
Um den Theil der Kraft zu finden, welcher den Punkt B in
der Richtung BE zu bewegen strebt, d.h., die
Kraft, welche die Raͤder in der Richtung ihrer Achsen treibt, koͤnnen
wir das Dreiek BAC als eine schiefe Flaͤche
betrachten, von welcher BC die Laͤnge, und
AB die Hoͤhe ist, und der ganze Druk
auf CB, welcher durch CB (1035) ausgedruͤkt werden kann, kann in zwei andere,
naͤmlich in AB und AC aufgeloͤst werden, welche die
respektiven Druke auf diese Linien (268 und 1000) ausdruͤken. Der Druk auf BC wird also bloß in dem Verhaͤltnisse von
1035 zu 1000, oder um ungefaͤhr 1/29 durch die Schiefe vermehrt, und das
Streben der Raͤder; sich in der Richtung ihrer Achse zu bewegen, ist, bei dem
gegenwaͤrtigen Winkel, das 268/1000 urspruͤnglichen Kraft, d.i., etwas
mehr als ein Viertel. Da aber der Laͤngenbewegung einer Achse durch einen
beinahe unsichtbaren Punkt, den man in ihrem Mittelpunkte anbringt, vorgebeugt
werden kann, so folgt, daß die Wirkung dieses Strebens beinahe gaͤnzlich
aufgehoben werden kann, und dieß ohne merklichen Verlust der wirkenden Kraft. Man
darf noch hinzufuͤgen, daß, bei vertikalen Achsen, diese Umstaͤnde
beinahe ihre ganze Wichtigkeit verlieren, indem jede Kraft, welche die eine niederzudruͤken und ihre Reibung zu vermehren
strebt, ebenso sehr die andere zu heben und ihren Gang
von ihrer Last zu befreyen strebt; ein Fall, dessen man sich mit ausgezeichnetem
Vortheile bedienen kann um einen groͤßeren Druk auf die langsam laufenden Achsen zu bringen, waͤhrend man denselben von den
schnelleren weg nimmt.
Wir gehen nun zu dem zweiten Saze. Die Wahrheit der in demselben enthaltenen
Behauptungen muß, wie ich wohl voraussezen darf, einleuchtend seyn, wenn man nur
zwei Kreise betrachtet, die sich wechselweise beruͤhren und an dem Punkte
ihrer Beruͤhrung mit ihrer gemeinschaftlichen Tangente zusammentreffen. Es
seyen A und B zwei solche
Kreise (Fig.
23.), welche einander in e beruͤhren.
AC ist die Linie, welche ihre Mittelpunkte
verbindet, und DF die gemeinschaftliche Tangente
derselben fuͤr den Punkt e. Sie bildet einen
rechten Winkel mit AC, und so auch die Umkreise
der beiden Kreise auf dem Punkte e: denn Kreise und
Tangenten fallen fuͤr einen Augenblik uͤber einander. Hieraus schließe
ich: 1tens, daß eine (bis zum Verschwinden kleine) Bewegung des gemeinschaftlichen Punktes dieser
drei Linien statt haben koͤnne, ohne deßwegen die Tangente DF nur einen Augenblik zu verlassen; und 2tens
daß, wenn eine unendliche Menge von Zaͤhnen an diesen Kreisen ist; diejenigen
Zaͤhne, welche sich in der Linie der Mittelpunkte finden, vorzugsweise besser
in einander eingreifen werden, als jene, die außer dieser Linie gelegen sind, weil
leztere die gemeinschaftliche Tangente und noch einen Zwischenraum zwischen sich
haben.
Die Wahrheit dieses Sazes (oder wenigstens eine unbestimmbare Annaͤherung zur
Wahrheit) laͤßt sich aus der Annahme herleiten, daß die beiden Kreise wirklich einander durchdringen. In dieser Hinsicht seyen
AB und ab in
Fig. 25.
zwei gleiche Kreise, welche parallel gegen einander in zwei sich beruͤhrenden
Ebenen liegen, so daß der eine den anderen in dem unbestimmbar kleinen krummlinigen
Raume defg dekt. Ich sage nun, daß, wenn der Bogen
dg unbestimmbar klein ist, die Umdrehung der
beiden Kreise nicht mehr Reibung zwischen den beiden sich beruͤhrenden
Flaͤchen gef und fdg erzeugt, als dann zwischen den beiden Kreisen
selbst statt haben wuͤrde, wann sie in einer und derselben Ebene
laͤgen und sich in dem Punkte n ihrer
gemeinschaftlichen Tangente beruͤhrten.
Denn, man ziehe die Linien DE, fd, dg, gf, ge, und gD, und in Hinsicht auf die bekannte Gleichung des
Kreises, sey dn = x,
gn = y und Dg = a, Abscisse,
Ordinate und Halbmesser des Kreises; so wird 2ax
– x² = y². Aus dieser Gleichung wird a = (y² + x²)/2x, wo der Nenner dieses Bruches, 2x, die Breite de ist, in welcher die
beiden Flaͤchen der zwei Kreise fdg und feg sich beruͤhren. Der Zaͤhler,
(y² + x²)
ist gleich dem Quadrate der Sehne gd
des Winkels EDg, welche Sehne ich z nenne. So wird a = z²/2x; und aus dieser Gleichung
entsteht die Proportion: a : z : : z : 2x = z²/a. Bei sehr
kleinen Winkeln kann man aber ohne merklichen Irrthum die Sinusse fuͤr die
Bogen nehmen; folglich mit noch weit mehr Grund die Sehnen; nehmen wir also den
Bogen dg oder die Sehne z unbestimmbar klein, so wird de = 2x = z²/a, oder unbestimmbar kleiner, d.h., um einen Grad in der
Ordnung der Infinitesimalen niedriger: denn es ist allgemein bekannt, daß das
Quadrat verschwindender Groͤßen unbestimmbar kleiner ist, als diese
Groͤßen es selbst sind. Wollen wir nun dieß hier anwenden, so wird, wenn die
Sehne z die Kreisentfernung zweier materiellen Theilchen
in dem schraubenfoͤrmigen Zahne ac des
Rades Bc
Fig. 23. (in
Hinsicht auf den Kreis ab in Fig. 25.)
ausdruͤkt, diese Entfernung z die mittlere
Proportionale zwischen dem Radius Dg eines solchen
Rades und dem doppelten Sinus vergus dieses undenkbar
kleinen Winkels seynIch
haͤtte vielleicht dieses Raisonnement bei der 25. Fig. mit der
Bemerkung beginnen sollen, daß jeder Entwurf eines Theiles einer Schraube
auf einer Flaͤche, welche auf die Achse einer solchen Schraube unter
einem rechten Winkel steht, ein Kreis ist; und daß folglich die Sehne z, oder die Linie gd der wahre Entwurf eines proportionalen Theiles irgend einer
Linie BC, Fig. 24. ist,
wenn sie um einen Cylinder von gleichem Durchmesser mit dem Kreise ab, Fig. 25.
geschlagen wird. A. d. O..
Ich weiß, daß einige Mathematiker behaupten, daß auch der kleinste Theil einer
krummen Linie nimmermehr genau auf eine gerade Linie fallen koͤnne: eine
Lehre, welche ich nicht
bestreiten will. Dem sey aber, wie ihm wolle, so ist es offenbar und gewiß, daß in
der materiellen Welt keine solche mathematische Krumme vorhanden ist, und daß es nur
Vieleke von einer groͤßeren oder geringeren Anzahl von Seiten gibt, je
nachdem naͤmlich die Dichtigkeit der verschiedenen Substanzen, die unter
unsere Sinne fallen, verschieden ist. Ich will daher fortfahren, die vorhergehende
Theorie zwar nicht auf die lezten Theilchen der Materie (deren Dimensionen ich nicht
kenne) sondern nur auf jene wirklichen Theilchen derselben anzuwenden, die man
bereits gemessen hat. Man weiß durch Versuche, daß ein Wuͤrfel Gold von einem
halben Zolle sich auf Silber zu einer Laͤnge von 1,442,623 Fuß ausdehnen
laͤßt, und dann noch zu einer Breite von 1/100 Zoll geflaͤtscht werden
kann. Rechnet man diese beiden Breiten zusammen, so gibt dieß 1/50 Zoll. Wenn wir
daher obige Laͤnge durch 25 theilen, so erhalten wir die Laͤnge eines
solchen Metallbandes von einem halben Zoll Breite, naͤmlich 47704 Fuß.
Schneiden wir dieses Band in Laͤngen von einem halben Zoll (oder
multipliciren wir mit 24, der Zahl der halben Zolle in einem Fuß) so erhalten wir
1,144,896 solche Quadrate, welche die Zahl der Blaͤtter in einem
halbzoͤlligen Wuͤrfel Gold ausmachen muͤssen: fuͤr die
Dike eines Zolles kommen deren 2,289,792. Wenn wir also ein Rad von Gold von 2 Fuß
im Durchmesser annehmen und die Reibung der Zaͤhne desselben bestimmen
wollen, muͤssen wir zuvoͤrderst die Zahl der Theilchen, die in den
Zahnen enthalten sind, welche sich auf einem Zolle des Umfanges des Rades befinden,
aufsuchen, und diese ist, wie wir so eben gesehen haben, 2,289,792 Blattdiken, oder
Durchmesser der Theilchen, die wir jezt betrachten wollen.
Wir haben also jezt das Verhaͤltniß, nach Fig. 24. 268 (AB) : 1035 (BC) : :
2,289,792 (der Zahl der Theilchen in einem Zolle Umfang der Basis): x = 8,843,040 Theilchen in jenem Theile die Linie BC, welche mit jenem Zolle des Umfanges
korrespondirt. Auf diese Weise ist also jedes der lezteren in der Richtung AB gemessenen Theilchen gleich 1/8,843,040 Zoll.
Nimmt man diesen Bruch fuͤr den Bogen gd,
Fig.
25., und will man hieraus die Laͤnge der Linie de (von welcher die Reibung dieses Zahnes so wie
aller uͤbrigen abhaͤngt) finden, so muͤssen wir uns folgender
Analogie bedienen; 12 Zoll (der Halbmesser des Rades) : 1/8,843,040 Zoll (der Sehne
gd) : : 1/8,843,040 Zoll (gd): de oder der
gesuchten Linie = 1/938,392,277,299,200 Zoll. Dieses Resultat ist noch immer von der
Wahrheit entfernt, da wir nicht wissen koͤnnen, um wie viel die lezten
Molekuͤln des Goldes noch kleiner sind.
Um nun auf einige Einfluͤsse dieses Systemes auf die Praxis aufmerksam zu
machen, will ich mir erlauben eine Form von Zaͤhnen vorzulegen, deren Spiel
allein schon ein hinlaͤnglicher Beweis der Wahrheit der vorausgeschikten
Theorie seyn wird. A und B
sind zwei Raͤder (Fig. 26.) deren
urspruͤngliche Kreise oder Eingriffs-Linie einander bei o beruͤhren. Da alle homologen Punkte eines
schraubenfoͤrmigen Zahnes sich in gleicher Entfernung von den Mittelpunkten
der Raͤder befinden, so darf ich den Zaͤhnen auch eine rhomboidale
Form geben, oti; und wenn der Winkel o rings um beide Raͤder derselbe ist, (wovon ich
bei DG durch Aufriß eine Idee zu geben
versuchteDer
Uebersezer findet nur D, kein DG im Orig. A. d. Ueb.), so
werden in diesem Falle nur diejenigen Theile, welche sich in der Ebene der Tangente
fh befinden, und unendlich nahe an der Ebene,
welche unter einem rechten Winkel durch die Mittelpunkte A und B auf dieselben laͤuft, einander
beruͤhren, und dort hat, wie wir bereits erwiesen haben, keine merkliche
Bewegung oder etwas, was Reibung erzeugen koͤnnte, zwischen den sich wirklich
beruͤhrenden Punkten statt. Ich moͤchte noch, wie die Figur auch
offenbar zeigt, hinzusezen, daß, wenn irgend eine solche Bewegung statt
haͤtte, die Winkel o einander verlassen und diese
Form von Zaͤhnen in der Anwendung ungereimt werden wuͤrde, und daß im
Gegentheile wenn solche Zaͤhne wirklich und mit Nuzen in der Praxis vorkommen
(was ich behaupten kann; haben ja sogar alle Zaͤhne in diesem Systeme eine
Tendenz, diese Form an ihren wirkenden Punkten anzunehmen) dieser Umstand
fuͤr sich selbst ein praktischer Beweis der Wahrheit der vorausgeschikten
Theorie und desjenigen ist, was ich hieruͤber sagte.
Man wird eingesehen haben, daß ich gewisser Massen dem Beweise meines dritten Sazes
Vorgriff, naͤmlich, daß die epikykloidal Form oder irgend eine andere
gegebene Form der Zaͤhne zu diesem Eingreifen nicht noͤthig ist. Es
ist offenbar, daß Zaͤhne von einer Epikykloidalform durch ihr Arbeiten mehr
convex werden muͤssen, indem die Basis der Krummen der einzige Punkt ist, wo
sie durch Reibung keine Abnuzung erleiden; waͤhrend Zaͤhne von jeder
anderen Form, wenn sie uͤber die urspruͤnglichen Kreise der
Raͤder reichen, gleichfalls eine Figur dieser Art durch das Abrunden ihrer
Spizen und das Aushoͤhlen der korrespondirenden Theile jener Zaͤhne,
welche sie treiben annehmen werden; und diese Operation wird so lang
fortwaͤhren, bis ein Winkel, der jenem bei o,
Fig. 26.
aͤhnlich ist, aber gewoͤhnlich etwas stumpfer ausfaͤllt, rings
um beide Raͤder entsteht, wo dann alle merkliche Veraͤnderung von Form
oder Verlust von Materie aufhoͤrt, wie die Raͤder, welche ich der
Gesellschaft vorlege, beweisen:
Rechts in der Zeichnung, Fig. 26.Im Originale
unten. A. d. Ueb., sind die Zaͤhne des Rades B ekig (hier vierekig) und die des Rades C
nach irgend einer Krummen s
innerhalb einer Epikykloide abgerundet. Alles, was ich
fuͤr diesen Fall zu bemerken habe, ist, daß die Zaͤhne in dem Rade B nicht uͤber ihren
urspruͤnglichen Kreis reichen duͤrfen, waͤhrend die
zugerundeten Theile der Zaͤhne des Rades C mehr
oder minder uͤber ihre urspruͤnglichen Kreise reichen; woraus offenbar
erhellt, daß der Beruͤhrungspunkt solcher Zaͤhne (wenn ihre Zahl
unendlich ist) einzig und allein in der Ebene der
gemeinschaftlichen Tangente unter rechten Winkeln auf AB faͤllt; ferner daß, wenn diese Zaͤhne hart genug sind um
dem gewoͤhnlichen Druke zu widerstehen und ohne in einander unter diesen
Umstaͤnden einzubeißen, kein Grund wahrzunehmen ist, warum die Form merklich
geaͤndert werden sollte, indem diese Beruͤhrung nur dort statt hat, wo
die beiden Bewegungen sowohl in Hinsicht auf Geschwindigkeit als Richtung einander
gleich sind. Eine Thatsache, die ich jezt anfuͤhren will, kann vielleicht
dieses Raͤsonnement bei einigen uͤberwiegen, aber gewiß nicht
schwaͤchen. Ich ließ zwei dieser Raͤder, die aus Messing verfertigt
wurden, mehrere Wochen lang unter einem bedeutenden Widerstande mit Schnelligkeit
treiben, und hielt sie stets mit Oel und Schmergel, einer der verderblichsten Mischungen
fuͤr Metalle, wenn sie damit gerieben werden, bestrichen; und nach diesem
gewiß strengen Versuche fand ich die Zaͤhne dieser Raͤder, an ihren Ursprunglichen Kreisen, eben so ganz wie vor dem
Versuche. Und warum? Gewiß aus keinem anderen Grunde, als weil sie ohne alle Reibung
arbeiteten.
Ich habe bisher nichts von Raͤdern in konischer Form gesprochen, die man bei
uns Muͤzen und Senkungs-Triebwerke (mitre et bevel
gur) nennt. Meine Modelle werden beweisen, daß ich sie in meinem Systeme
eingeschlossen habe. Die einzige Bedingung bei dieser Einheit von Grundsaͤzen ist, daß die
Achsen zweier Raͤder, statt parallel gegen
einander zu stehen, immer in derselben Ebene liegen
muͤssen. Unter dieser Bedingung hat jede oben erwaͤhnte Eigenschaft
auch bei dieser Klasse von Raͤdern statt, welche meine Methode gleichfalls
umfaßt, so wie sie uͤberhaupt alle moͤglichen Faͤlle von
Getrieben in sich begreift.
Um die Graͤnzen dieser Abhandlung nicht zu uͤberschreiten, habe ich
einen Theil derselben unterdruͤkt und erlaube mir nur noch einige wenige
Bemerkungen uͤber die Anwendung dieser Raͤder in praktischer Hinsicht.
Ich habe sie bei verschiedenen wichtigen Maschinen anwenden gesehen, und fand, daß
sie denselben Schnelligkeit, sanfte Bewegung und hohe Genauigkeit in dieser lezteren
ertheilten. Ja sie leisteten noch mehr. Sie ließen nicht unbedeutende Maschinen
entstehen, welche ohne sie nie an das Licht getreten seyn wuͤrden. Bei
schnellen Bewegungen leisten sie, mit mathematischer Genauigkeit und großer
Kraftersparung, alles was Schnur und Riemen leisten kann; Eigenschaften, die
vorzuͤglich fuͤr Spinnereyen interessant seyn muͤssen, und
fuͤr Calico-Drukereyen, deren zarte Operationen die groͤßte
Genauigkeit in der Bewegung fordern. In der Uhrmacherey ist diese Eigenschaft von
hoher Wichtigkeit um die Wirkung der Gewichte zu regeln, und der Kraft, welche
Gleichfoͤrmigkeit erzeugen soll, sie mag worinn immer bestehen, vollkommen
freyen Spielraum zu geben. Ja ich darf sagen, daß sie beinahe jede Ursache einer
Anomalie vernichten, indem eine gegebene Uhr mit weniger dann einem Viertel des
gewoͤhnlich gebrauchten Gewichtes gehen wird. In
Flaͤtsch-Muͤhlen, wo eine Walze durch den Triebstok der anderen
getrieben wird, ist die Platte, welche durch die Walzen durchlaufen soll, in
staͤtem Kampfe mit dem gewoͤhnlichen Triebwerke, das mehr oder minder
convulsivisch arbeitet: dadurch wird die Platte runzelig, und der Widerstand
neuerdings vermehrt: diese Nachtheile fallen bei meinem Getriebe weg. Ich
koͤnnte noch mehrere aͤhnliche Faͤlle anfuͤhren,
schließe aber mit dem Wunsche, etwas zur Verbesserung und Vervollkommnung der
Manufakturen dieser Gegend und zu dem Wohle meines geliebten Vaterlandes beigetragen
zu haben.
Tafeln