| Titel: | Ueber Dampfbothe. Von Thom. Tredgold, Esqu. und Baumeister. |
| Fundstelle: | Band 19, Jahrgang 1826, Nr. XXII., S. 114 |
| Download: | XML |
XXII.
Ueber Dampfbothe. Von Thom. Tredgold, Esqu. und
Baumeister.
Aus dem Edinburgh Philosophical Journal. October.
1825. S. 244.
Mit Abbildungen auf Tab.
IV.
Tredgold, uͤber Dampfbothe.
Die Anwendung der Dampfmaschine zum Treiben der Schiffe ist
eine jener Erfindungen, welche unser Zeitalter charakterisirt, und uns einladet, auf
Erleichterung der Verbindung mit anderen Voͤlkern zu denken, wodurch unser
Wohlstand unendlich gewinnen muß. Bisher hingen wir lediglich von der
natuͤrlichen Gewalt der Winde und der Wogen ab; Unsicherheit und Gefahr des
Lebens und des Eigenthums laͤhmte unsere mercantilischen Unternehmungen; es
hemmte sie zwar nicht, aber es machte die Gefahr sicherer Bestellung maͤchtig
groß, es machte sie eben dadurch kostbar, zeitfressend und langweilig.
Der hohe Vortheil einer Triebkraft innerhalb des Schiffes, einer Kraft, die
gaͤnzlich in der Gewalt derjenigen ist, die sie leiten, ist zu einleuchtend,
als daß man bei Entwickelung desselben verweilen duͤrfte: diese Kraft kann
nach Belieben erhoͤht und vermindert, und noͤthigen Falles sogar
gaͤnzlich beseitigt werden. Sie kann gegen Winde und Wogen gerichtet werden,
und gewaͤhrt eben dadurch ein Rettungsmittel aus dem Kampfe der Elemente,
wenn diese mit vereinten Kraͤften den sicheren Landungsplatz streitig machen
wollen. Insofern uns diese Kraft ein sicheres und gewisseres Mittel zur
Foͤrderung unserer Guͤter darbiethet, hat es uns auch zugleich einen
neuen Antrieb zu dem wichtigen Studium der Gesetze der Bewegung im Wasser, und der
Grundsaͤtze der Theorie der Schiffbaukunst verliehen.
Man hat gesagt, daß die Englaͤnder in diesem Zweige des wissenschaftlichen
Wissens weniger vorgeruͤckt sind, als andere Voͤlker, und diese
Bemerkung enthaͤlt vielleicht einiges Wahre; denn die Kunst wurde bisher in
England nur sehr nachlaͤssig durch Wissenschaft geleitet.Man wird dieß befremdend finden, es ist aber sehr wahr, und nur zu tief in
dem mangelhaften Zustande der englischen Universitaͤten
gegruͤndet.A. d. U. Man faͤngt nun eben erst an die Wichtigkeit wissenschaftlicher
Kenntnisse bei uns zu fuͤhlen, und wir wollen hoffen, daß sie, in
Baͤlde, bei uns mit mehr Erfolg als in jedem andern Lande und in jedem
anderen Zeitalter betrieben werden wird. Es ist sehr zu wuͤnschen, daß irgend
ein der Sache gewachsener Schriftsteller die Grundsaͤtze der reinen
Wissenschaft in eine Form bringt, die fuͤr praktische Anwendung derselben
brauchbar ist, und die Wahrheiten der Physik auf die klarste, deutlichste und
einfachste Weise lehrt: nicht in den verschlungenen Knoten der Systeme, sondern in
der freisten und ungebundesten Form. Man darf nicht vergessen, daß der Hauptzweck
des Praktikers darin besteht, sich die Methoden, durch welche man die Gesetze, nach
welchen die Natur arbeitet, entdecken kann, eigen zu machen, die
Verhaͤltnisse derselben zu bestimmen, und Kraͤfte, Bewegungen und
Wirkungen in den einzelnen Faͤllen, in welchen sie im Leben vorkommen, zu
bemessen und zu berechnen. Kenntnisse dieser Art fordern nicht soviel
vorlaͤufiges systematisches Studium, als man gewoͤhnlich glaubt; sie
werden vielmehr, einzig und allein, durch Praxis auf die wohlthaͤtigste Weise
erworben und vervollkommnet. Ohne die Natur fleißig um Rath zu fragen, kann man sie
nicht mit irgend einem Vortheile erweitern, und daher wird man nothwendig auf die
genaueste Beobachtung der Erscheinungen der Natur geleitet. „Der Mensch,
als Diener und Dolmetscher der Natur, versteht nur soviel von der Ordnung der
Natur, und handelt nur insofern nach derselben, als er dieselbe mit
Beihuͤlfe der Erfahrung und des Verstandes beobachtet hat;“
seine Bemuͤhungen muͤssen lediglich auf Leitung und Anpassung der
Wirkung der Naturkraͤfte beschraͤnkt bleiben. Die Untersuchung dieser
Kraͤfte, dieser Ursachen wird oft sehr schwer, und daher ist auch die
kuͤrzeste, die bestimmteste, die allgemeinste Art daruͤber zu
urtheilen diejenige, die am sichersten zum Zwecke fuͤhrt; durch diese Art zu
urtheilen sind die reinen Wissenschaften zu ihrem hohen Grade von Vollkommenheit
gelangt; ich meine durch die geometrische und analytische Methode zu denken. Durch
Zeichen und Buchstaben liefert der Algebrist ein gedraͤngtes und treues Bild des Standes seiner
Aufgabe: das Verdienst, das seiner Methode allein eigen ist, ist Deutlichkeit und
allgemeine Guͤltigkeit. Der Geometer erreicht seinen Zweck durch Linien und
Figuren und beruft sich auf die Sinne um die Richtigkeit seiner Schluͤsse zu
beweisen. Jede dieser Methoden hat ihre Vortheile; aber bei weiten am besten ist es,
beide zu verbinden, indem die allgemein guͤltigen Schluͤsse der einen
durch die andere nicht selten auch den Sinnen anschaulich gemacht werden
koͤnnen.
Um jedoch zu dem Gegenstande dieses Aufsatzes zuruͤckzukehren, so wird man
leicht begreifen, daß die Bewegung der Dampfbothe, ihre Formen und
Verhaͤltnisse ein schoͤnes Feld zur Anwendung der reinen Wissenschaft
darbiethen, und die Bemerkungen erlaͤutern, die wir so eben uͤber die
Vortheile eines Wissens, das mehr auf richtigen Begriffen von den Wirkungen der
Naturkraͤfte, als auf systematische Schul-Weisheit beruht, gewagt haben. Wir
wollen uns hier damit beschaͤftigen, den Widerstand bei verschiedenen
Geschwindigkeiten in stillem Wasser zu finden, und zugleich auch die
zweckmaͤßigste Geschwindigkeit fuͤr die Ruder; die Lage und Zahl der
Ruder; den Widerstand bei verschiedenen Geschwindigkeiten in Stroͤmen und
Stroͤmungen; die Geschwindigkeit der Ruder endlich fuͤr jeden dieser
Faͤlle.
Man kann annehmen, daß der Widerstand eines und desselben Schiffes, bei stillem
Wasser, sich so ziemlich verhaͤlt, wie das Quadrat der Geschwindigkeit; die
Abweichung von diesem Gesetze ist zu unbedeutend, als daß sie innerhalb der
Graͤnzen der praktisch vorkommenden Geschwindigkeiten einen merklichen
Einfluß aͤußern koͤnnte. Denn also a die Kraft ist, welche das Schiff in einer gleichfoͤrmigen
Bewegung mit der Geschwindigkeit u
erhaͤlt, so wird die Kraft, welche es mit der Geschwindigkeit v in Bewegung erhaͤlt, durch folgendes
Verhaͤltniß gefunden:
u² : v² : :
a : av²/u² = dem Widerstande bei der Geschwindigkeit v.
Nun wirkt diese Kraft mit der Geschwindigkeit v; folglich
ist die mechanische Kraft, welche erforderlich ist, um das Both mit der
Geschwindigkeit v in Bewegung zu erhalten, av³/u².
Hieraus erhellt, daß die mechanische Kraft, oder die Kraft der Dampfmaschine, die ein
Both in stillem Wasser treiben soll, sich wie der Cubus der Geschwindigkeit verhalten muß. Wenn
also eine Maschine von der Kraft von 12 Pferden ein Both im stillen Wasser in Einer
Stunde sieben (engl.) Meilen weit treibt, und man will wissen, welche Kraft
noͤthig ist um dasselbe Both zehn Meilen weit in Einer Stunde zu treiben, so
hat man 7³ : 10³ : : 12 : (10³ × 12)/7³ = 35;
oder eine Maschine von der Kraft von 35 Pferden.
Diese ungeheuere Zunahme an Kraft um eine so geringe Zunahme an Geschwindigkeit zu
erhalten muß nothwendig Einfluß auf die Festsetzung der Geschwindigkeit fuͤr
ein zu langen Reisen bestimmtes Both haben, und die Verhaͤltnisse der Theile
desselben muͤssen nach dieser Geschwindigkeit so berechnet werden, daß noch
ein gehoͤriger Ueberschuß an Kraft fuͤr unvorgesehene Zufaͤlle
uͤbrig bleibt. Wo Guͤter und Reisende zu fahren sind, sollte man eine
geringere Geschwindigkeit waͤhlen. Dieß erhellt aus obigem Beispiele auf eine
auffallende Weise: denn, um die Geschwindigkeit eines und desselben Bothes von 7
Meilen auf 10 in Einer Stunde zu bringen, hat man beinahe drei Mal mehr Kraft, und
folglich drei Mal mehr Brenn-Material und drei Mal mehr Raum zum Unterbringen
desselben noͤthig, den groͤßeren Raum fuͤr eine groͤßere
Maschine ungerechnet. Wenn daher sieben Meilen in Einer Stunde fuͤr die
Bestimmung des Schiffes bei seiner Fahrt zureichen, sind die Vortheile bei dieser
geringeren Geschwindigkeit einleuchtend.
Nach den Grundsaͤtzen, nach welchen wir rechneten, ist die Kraft, welche
noͤthig ist, um einem Bothe verschiedene Geschwindigkeiten zu geben, bei
stillem Wasser, folgende
fuͤr
3
Meilen
in
Einer
Stunde
eine
Kraft
von
5 1/2
Pferden.
–
4
–
–
–
–
–
–
–
13
–
–
5
–
–
–
–
–
–
–
25
–
–
6
–
–
–
–
–
–
–
43
–
–
7
–
–
–
–
–
–
–
69
–
–
8
–
–
–
–
–
–
–
102
–
–
9
–
–
–
–
–
–
–
146
–
–
10
–
–
–
–
–
–
–
200
–
Bei kleinen Reisen ist die Groͤße des Raumes, welche man der Cajuͤte
fuͤr die Maschine und dem Bothe zur Aufbewahrung der Kohlen wegen der
vermehrten Geschwindigkeit geben muß, nicht von Bedeutung; bei langen Reisen
hingegen wird der brauchbare Schiffsraum so verengert, daß es zweifelhaft wird, ob Dampfbothe dazu
tauglich sind, oder nicht. Der Verbrauch an Brenn-Material ist, um eine bestimmte
Wirkung hervorzubringen, an Dampfmaschinen auf Dampfbothen weit groͤßer, als
auf dem Lande: vielleicht bloß wegen Unvollkommenheit des Zuges im Schornsteine und
des beschraͤnkten Raumes fuͤr den Kessel. Dem ersteren Fehler ließe
sich vielleicht leicht durch ein kuͤnstliches Geblaͤse abhelfen, das
so eingerichtet waͤre, daß es die Flamme noͤthigt, ihre Hitze an dem
Kessel anzubringen. Wir koͤnnen bei dieser Gelegenheit nicht umhin zu
bemerken, daß es allerdings der Aufmerksamkeit derjenigen, welche die Dampfbothe
verbessern wollen, werth ist, ein zweckmaͤßigeres Verfahren anzuwenden um die
Hitze mehr auf ihren Gegenstand zu beschraͤnken, vorzuͤglich dort, wo
der Maschinist und der Heitzer derselben ausgesetzt sind.
Wenn die Ruder eines Dampfbothes in Thaͤtigkeit sind, gibt es einen Punkt in
jedem Ruder, in welchem, wenn die ganze Gegenwirkung des Wassers darin concentrirt
waͤre, die Wirkung nicht veraͤndert wird; diesen Punkt kann man den
Mittelpunkt der Gegenwirkung nennen. Dieser Punkt wurde fuͤr den
gegenwaͤrtigen Fall nicht bestimmt, kann aber vielleicht in der Folge ein
Gegenstand unserer Untersuchung werden.
Wir nehmen an, daß das Wasser in Ruhe und die Geschwindigkeit dieses Mittelpunktes
der Gegenwirkung, V, die Geschwindigkeit des Bothes, v, ist; so ist nothwendig, V
– v, die Geschwindigkeit, mit welcher die Ruder
auf das Wasser schlagen. Nun ist aber der Unterschied zwischen der Geschwindigkeit
der Ruder und der Geschwindigkeit des Bothes gleich der Geschwindigkeit mit welcher
die Ruder auf das Wasser wirken. Wenn, folglich, diese Geschwindigkeiten gleich
sind, so haben die Ruder keine Kraft das Both zu treiben, und, wenn sich die Ruder
noch langsamer bewegen, wuͤrden sie das Both aufhalten. Da nun (V – v), die
Geschwindigkeit ist, so ist die Kraft der Gegenwirkung (V – v)²; denn diese
Groͤße steht im Verhaͤltnisse zu dem Drucke, der die Geschwindigkeit,
V – v, erzeugt.
Allein, waͤhrend der Wirkung des Ruders gibt das Wasser mit der
Geschwindigkeit, V – v, nach, und da die Geschwindigkeit des Bothes, v, ist, so ist die wirkliche Kraft wie V
– v : v : : (V – v)² : v (V – v). Die Wirkung dieser Kraft in einer gegebenen Zeit ist
ein Maximum, wenn v² (V – v) ein Maximum ist, d.h., wenn 2
V = 3 v ist, oder wenn die Geschwindigkeit
des Mittelpunktes der Gegenwirkung der Ruder anderthalb Mal die Geschwindigkeit des
Bothes ist.
Es ist sehr zu wuͤnschen, daß die Wirkung der Ruder so gleichfoͤrmig
und staͤtig als moͤglich ist, außer sie waͤren so vorgerichtet,
daß die Wandelbarkeit der Kraft der Maschine mit der Wandelbarkeit der Wirkung der
Ruder zusammentrifft. Allein, wenn man die Wirkung der Ruder so
gleichfoͤrmig, wie moͤglich, machen will, darf ihre Zahl nicht
groͤßer werden, als fuͤglich vermieden werden kann, weil dann das
Wasser keine Zeit hat dazwischen zu fließen, so daß es eine gehoͤrige Summe
von Gegenwirkung hervorbringen koͤnnte, und weil sie sich auch bei ihrem
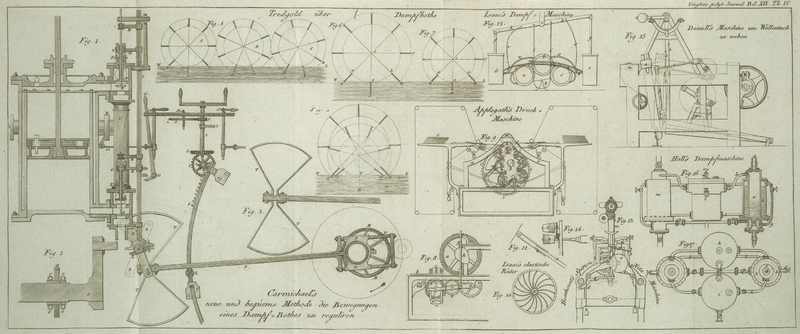
Austritte aus dem Wasser nicht so gut reinigen. Wenn wir annehmen, daß, W L, in Fig. 2, Taf. IV. die
Wasserlinie ist, wenn das Wasser in Ruhe ist, so scheint die vortheilhafteste
Vorrichtung, bei der geringsten Anzahl von Rudern, diese, daß man das Ruder, A, des Rades, A, gerade in
das Wasser eingreifen laͤßt, wenn das vorhergehende Ruder, B, in senkrechter Lage, und das Ruder, C, gerade am Austritte ist. Bei dieser Vorrichtung hat
das Wasser Zeit dazwischen zu fließen, und von dem sich zuruͤckziehenden
Ruder zu entweichen. Wenn man eine geringere Anzahl anwendet, so wird ein kurzer
Zwischenraum in der Zeit entstehen, waͤhrend welcher keines der Ruder in
voller Thaͤtigkeit waͤre. Die aͤußerste Abweichung wird
zwischen der Stellung der Raͤder, A, und, B,
Fig. 2, Statt
haben; einen Mittelstand zeigt das Rad, C. Ich habe
nicht versucht, den wirklichen Stand der Oberflaͤche des Wassers
waͤhrend der Bewegung der Ruder darzustellen; denn, wenn dieß nicht mit aller
Genauigkeit nach der Natur geschieht, so ist es besser, man laͤßt es bleiben:
indessen hat die Form der Oberflaͤche auch keinen materiellen Einfluß auf die
Schluͤsse.
Die Bestimmung des Halbmessers des Rades, oder der Tiefe der Ruder, bei einer
gegebenen Anzahl derselben, ist eine leicht zu loͤsende Aufgabe, wenn die
vorausgegangenen Bedingungen gehoͤrig beachtet werden. Denn, man setze AC, Fig. 3, den Halbmesser, =
r, und x = der Tiefe des
Ruders, Aa, die Anzahl der Ruder, = n, so wird 360°/n dem
Winkel AOB, der zwischen den beiden Rudern
eingeschlossen ist, und
r Cos. 360/n = O a, da der Cosinus des Winkels die Tiefe von dem
Mittelpunkte des Rades zur Oberflaͤche des Wassers ausdruͤckt;
und,
r Cos. 360/n = r – x,
oder
r (1 – Cos. 360/n) = x = Aa, der Tiefe der Ruder.
Es ist auch x/(1 – Cos. 360/n) = r = AO, dem Halbmesser
des Rades.
Aus diesen Gleichungen ergeben sich folgende Regeln, naͤmlich: um den
Halbmesser des Rades bei gegebener Anzahl und Tiefe der Ruder zu finden, theilt man
360 durch die Anzahl der Ruder, wodurch man die Grade des zwischen den beiden Rudern
enthaltenen Winkels erhaͤlt, zieht von der Einheit den natuͤrlichen
Cosinus dieses Winkels ab, und theilt die Tiefe der Ruder durch den Rest: der
Quotient ist der Halbmesser des Rades.
Wenn also, z.B., die Zahl der Ruder 8, ihre Tiefe 1 1/2 Fuß ist, so ist 360/8 =
45°. Der Cosinus hiervon ist = 0,7071; folglich wird 1,5/(1 – 0,7071)
= 5,12 Fuß, fuͤr den Halbmesser des Rades.
Ebenso, wenn die Zahl der Ruder 7, ihre Tiefe 1 1/2 Fuß ist, wird, wie vor, 360/7 =
51°26'; der Cosinus hiervon ist 0,6234; folglich 1,5/(1 – 0,6234) = 4
Fuß.
Beide Theilungen sind in Fig. 4 dargestellt, und,
man muß bemerken, daß, wenn die Tiefe der Ruder festgesetzt ist, eine
groͤßere Anzahl derselben den Vorzug verdient, weil dann der erste Eindruck
auf das Wasser weniger senkrecht geschieht. Man wird diesen Unterschied leicht
sehen, wenn man die Winkel, unter welchen die Ruder, A,
und, a, in Fig. 4 auf das Wasser
schlagen, unter einander vergleicht. Man wird auch bemerken, daß das groͤßere
Rad weniger Neigung hat, das Wasser hinter, C, in die
Hohe zu werfen.
Es ist offenbar, daß, wenn man das Rad vergroͤßert, die Schiefheit der Wirkung
bei dem Eintritte in das Wasser vermindert wird; dieß kann aber auch dadurch geschehen, daß man die
Tiefe der Raͤder verringert, wie aus Fig. 6 und 7 erhellt, wo in beiden
Raͤdern dieselben Winkel sind. Es ist daher sehr gut, wenn man die Tiefe
finden kann, und, wenn die Zahl der Raͤder und der Halbmesser des Rades
gegeben ist, findet man dieselbe durch folgende Regel:
Man multiplicirt den Halbmesser des Rades mit der Differenz zwischen der Einheit und
dem natuͤrlichen Cosinus des zwischen den beiden Rudern eingeschlossenen
Winkels; das Produkt gibt die verlangte Tiefe. Es sey der Halbmesser 4,5 Fuß, und
die Zahl der Ruder 8; so wird 4,5 (1 – 0,7071) = 1,318 Fuß fuͤr die
Tiefe der Ruder.
Ich denke 8 Ruder sind die geringste Zahl, die man annehmen kann, und, wo große
Raͤder angewendet werden koͤnnen, kann man neun bis zehn derselben
brauchen; wo aber viele Raͤder gebraucht werden, muͤssen die
Raͤder nothwendig von großem Durchmesser seyn, damit die Ruder
gehoͤrig getrieben werden koͤnnen. Die Vortheile bei Raͤdern
von großem Durchmesser bestehen in der guͤnstigen Richtung, in welcher sie
auf das Wasser schlagen und aus demselben treten; die Ruder sind auch mehr von
einander entfernt, und da sie mehr Gegenwirkung an dem Wasser finden, so zerspritzen
sie dasselbe weniger; selbst das Gewicht des Rades, das als Regulator der darauf
wirkenden Kraͤfte dient, macht es wirksamer. Im Gegentheile lassen sich aber
auch einige sehr bedeutende Einwuͤrfe gegen sehr große Raͤder an
See-Schiffen machen; sie lassen der Gewalt der Wogen mehr Herrschaft uͤber
die Maschine; sie sind eine wahre Last und sehen schlecht aus; sie heben den
Wirkungs-Punkt zu hoch uͤber die Wasserlinie, so daß man bei der Wahl
derselben Erfahrung sowohl, als Urtheilskraft wohl zu Rath ziehen muß.
Die beste Lage fuͤr die Ruder scheint die einer Flaͤche zu seyn, die
durch die Achse laͤuft, so wie sie in den Figuren gezeichnet ist; wenn sie in
einer Ebene sind, die nicht mit der Achse zusammentrifft, so muͤssen sie
sowohl mehr schief auf das Wasser bei ihrem Eintritte in dasselbe schlagen, als auch
eine bedeutende Menge Wassers mit sich in die Hoͤhe heben, wenn sie dasselbe
verlassen. Hinsichtlich der Form des Ruders ist es klar, daß sie von der Art seyn
muß, daß der Widerstand gegen die Bewegung derselben der moͤglich
groͤßte werden muß, und der Druck von hinten der moͤglich kleinste.
Diese Bedingungen scheinen in einem hohen Grade dadurch erfuͤllt zu werden, daß man die
einfachste unter allen Formen, das Rechteck, anwendet: wir koͤnnen aber
vielleicht noch vieles hieruͤber durch eine mit Geist angelegte Reihe von
Versuchen lernen.
Da bei der Kraft der Gegenwirkung gegen die Ruder einiger Wechsel Statt hat, so kann
man, gewisser Maßen, denselben dadurch ausgleichen, daß man die Perioden desselben
mit dem Wechsel in der Kraft der Maschine zusammen treffen laͤßt. Um dieß zu
bewirken, sollte der Stoß der Maschine in derselben Zeit geschehen, welche jener
Theil der Umdrehung des Ruder-Rades ausfuͤllt, den man durch einen Bruch
ausdruͤcken kann, in welchem die Zahl der Ruder der Neuner ist, und der
Staͤmpel sollte sich an dem Ende seines Stoßes befinden, wann eines der Ruder
senkrecht steht. Denn, wann eines der Ruder senkrecht steht, wie in dem Rade, A,
Fig. 5, so ist
die Gegenwirkung am kleinsten, und sie ist am groͤßten, wann zwei Ruder
gleich tief eingesenkt sind, wie bei dem Rade, B, zu
welcher Zeit dann die Kraft unter rechten Winkeln auf die Kurbel wirken wird.
Nachdem wir nun gezeigt haben, welche Kraft erfordert wird, um ein Both in stillem
Wasser in Bewegung zu erhalten, wird es nicht ohne Nutzen seyn, diese Untersuchung
auch fuͤr den Fall auszudehnen, wo das Both sich in einem Strome oder in
einer Stroͤmung bewegt. Man setze fuͤr diesen Fall, die
Geschwindigkeit des Bothes = v, die Geschwindigkeit des
Stromes = c, und den Widerstand = a, wenn sich das Both mit der Geschwindigkeit, u, bewegt.
Der Widerstand, der dann uͤberwunden werden muß, um dem Bothe die
Geschwindigkeit, v, zu geben, ist, wenn die Bewegung
nach der Richtung des Stromes Statt hat,
Textabbildung Bd. 19, S. 121
Und, wenn das Both sich gegen den Strom bewegen soll, wie
Textabbildung Bd. 19, S. 121
Folglich ist die Kraft, fuͤr beide Faͤlle, ausgedruͤckt
durch
Textabbildung Bd. 19, S. 121
Das obere Zeichen gilt, wenn die Bewegung nach der Richtung des Stromes geschieht,
und das untere, wenn die Bewegung gegen den Strom gerichtet ist. Wenn, c, oder die Geschwindigkeit des Stromes = Null ist, ist das
Resultat dasselbe wie zuvor. Allein der Widerstand in stillem Wasser ist nicht das
Mittel zwischen den Widerstaͤnden in der Richtung des Stromes und gegen den
Strom; folglich muß der mittlere Gang eines Bothes, welches abwechselnd mit dem
Strome und gegen denselben faͤhrt, weniger betragen, als der mittlere Gang im
stillen Wasser. Der mittlere Widerstand ist
Textabbildung Bd. 19, S. 122
waͤhrend der Widerstand in stillem Wasser nur av³/2, und die Differenz zwischen beiden avc²/u² ist;
eine Groͤße, welche von der Geschwindigkeit des Stromes abhaͤngt, und
fuͤr jeden besonderen Fall nach der mittleren Bewegung des Stromes berechnet
werden muß.
Wenn ein Both nach der Richtung des Stromes getrieben wird, so ist die
Geschwindigkeit, mit welcher die Ruder auf das Wasser wirken, V + c – c;
und wenn das Both gegen den Strom treibt, so wird sie V
– c – v;
folglich in jeder Richtung, V ± c – v; und als Kraft
des Widerstandes (V ± c – v)². Allein, der wirkliche
Widerstand des Bothes ist, wie V ± c – v : v : : (V ± c – v)² : v (V ± c – v); und die
Wirkung hiervon ist in einer gegebenen Zeit ein Maximum, wenn v² (V + c
– v) ein Maximum ist, d.h., wenn
Textabbildung Bd. 19, S. 122
oder, wenn V = 1,5 v ∓ c. Auch wenn
Textabbildung Bd. 19, S. 122
Wenn c = o, oder das Both in
stillem Wasser sich bewegt, ist 2V/3 = v, wie oben, und das Mittel zwischen Bewegung mit dem
2V/3 = v. Strome und
gegen den Strom ist gleichfalls 2V/3 = v. Wenn daher die Geschwindigkeit nicht
veraͤndert werden kann, um sie den Umstaͤnden anzupassen, so ist dieß
fuͤr jeden Fall das beste Verhaͤltniß. Wo die Staͤrke des
Stromes bedeutend ist, waͤre es sehr zu wuͤnschen, daß man im Stande
waͤre, die Geschwindigkeit der Raͤder veraͤndern zu
koͤnnen, was durchaus nicht durch eine Veraͤnderung in der
Geschwindigkeit des Staͤmpels der Dampfmaschine geschehen sollte, weil bei
jeder Veraͤnderung an der Geschwindigkeit desselben die Kraft der Maschine
leidet. Es ist durchaus nicht schwer, eine solche Vorrichtung des Mechanismus zu treffen, daß dadurch die
erforderliche Veraͤnderung in der Geschwindigkeit erzeugt wird; diese
Vorrichtung kann so stark und dauerhaft seyn, als die bisher gewoͤhnliche,
ohne daß sie theurer zu stehen kaͤme, wenn man naͤmlich die Vortheile
erwaͤgt, die man dadurch erhaͤlt. Man darf nur fuͤr Vermehrung
der Geschwindigkeit sorgen; denn, wenn das Both mit dem Strome faͤhrt, so ist
die Geschwindigkeit der Ruder bereits zu groß, waͤhrend, wenn es gegen den
Strom fahren muß, sowohl eine Vergroͤßerung der Geschwindigkeit des Rades,
als der Oberflaͤche des Ruders nothwendig wird, wo man den mittleren Gang
halten will.
Ich will diesen Aufsaz mit einem Blike auf die Geschwindigkeit beschließen, welche
ein Both erhalten kann, wenn die Kraft dieselbe bleibt. Es sey, P, die Kraft der Maschine, so wird dann
Textabbildung Bd. 19, S. 123
Es sey das Verhaͤltniß der Geschwindigkeit des Stromes zu der Geschwindigkeit
des Bothes, wie 1 : n; d.h., 1 : n : : v : c = nv. Daraus wird
Textabbildung Bd. 19, S. 123
Wenn das Both sich in einem Strome bewegt, dessen Geschwindigkeit, n, Mahl die Geschwindigkeit des Bothes ist, so haben
wir
Geschwindigkeit des Stromes
Geschwindigkeit des Bothes
mit dem Strome,
4 (engl.) Meilen
8 Meilen in Einer Stunde.
in Einer Stunde:
2,2 – –
– –
6,6 – –
– –
1,53 – – –
–
6,12 – – –
–
Stilles Wasser
0,00 – – –
–
5,00 – – –
–
Gegen den Strom
1,08 – – –
–
4,34 – – –
–
1,38 – – –
–
4,16 – – –
–
2,38 – – –
–
3,58 – – –
–
3,17 – – –
–
3,17 – – –
–
Diese Tafel zeigt, daß eine Kraft, die ein Both, in stillem Wasser, mit einer
Geschwindigkeit von fuͤnf Meilen in Einer Stunde zu bewegen vermag, dasselbe
nur mit einer Geschwindigkeit von wenig mehr als 3 Meilen gegen einen Strom zu
treiben vermag, der gleiche Geschwindigkeit mit dem Bothe hat, und daß die
Geschwindigkeit desselben Bothes 8 Meilen in Einer Stunde betraͤgt, wenn
dasselbe nach der Richtung eines Stromes laͤuft, dessen Geschwindigkeit vier
Meilen in einer Stunde betraͤgt. Man muß bemerken, daß diese Berechnungen die
Flaͤche der Raͤder und ihre Geschwindigkeit als nach den
Verhaͤltnissen des Maximums fuͤr jeden Fall gestellt voraussezen; denn
sonst wuͤrde die Geschwindigkeit mit dem Strome vergroͤßert und gegen
denselben vermindert.
Es bleiben hier noch viele wichtige Umstaͤnde zu eroͤrtern
uͤbrig, wie z.B. die Form des Bothes, damit es sich mit dem mindesten
Widerstande bewegen kann, der wirkliche Widerstand, der von der Form und von der
Ladung abhaͤngt, und die Lage der Raͤder, um die beste Wirkung
hervorzubringen.
Tafeln