| Titel: | Untersuchungen über die Theorie der Hydro-Dynamik. |
| Fundstelle: | Band 22, Jahrgang 1826, Nr. I., S. 1 |
| Download: | XML |
I.
Untersuchungen uͤber die Theorie der
Hydro-Dynamik.
Von Thomas Tredgold, Esqu.
Aus dem Philosophical Magazine and Journal. Julius.
1826. S. II.
Mit einer Abbildung auf Tab. II.
Tredgold's, Untersuchungen uͤber die Theorie der Hydro-Dynamik.
Ich erlaube mir einige Bemerkungen uͤber die
Grundsaͤze, die man gewoͤhnlich als Basis der Theorie des Widerstandes
der Fluͤßigkeiten betrachtet. Es ist bekannt, daß diese Grundsaͤze von
den Resultaten der Erfahrung abweichen, und es ist so wichtig, den Widerstand der
Fluͤßigkeiten auf feste Grundsaͤze zuruͤkzufuͤhren, daß
man natuͤrlich erwarten sollte, dieser Gegenstand muͤßte
laͤngst mit mehr als gemeiner Sorgfalt untersucht worden seyn. Unter dieser
Voraussezung geschieht es nicht ohne eine gewisse Aengstlichkeit, daß ich die Art,
wie man bei diesen Grundsaͤzen schloß, einer Pruͤfung unterziehe.
Alle hierher gehoͤrigen Grundsaͤze lassen sich auf Prop. 34 Book II. von Sir.
Isaac Newton's
Principles of Natural Philosophy
zuruͤkfuͤhren. Wenn es mir nun gelingt zu zeigen, daß dieser Saz nicht
gehoͤrig erwiesen ist, so muͤssen alle uͤbrigen daraus
abgeleiteten nothwendig eben so unrichtig seyn.
Der Saz heißt so: „Wenn in einem duͤnnen Mittel, welches aus
gleichen in gleichen Entfernungen frei von einander gestellten Theilchen
besteht, eine Kugel und ein Cylinder, welche beide gleichen Durchmesser haben,
sich mit gleichen Geschwindigkeiten in der Richtung der Achse des Cylinders
bewegt, so ist der Widerstand der Kugel nur halb so groß, als der des
Cylinders.“
Der Beweis dieses Sazes, so wie er in den Principles of
Natural Philosophy gegeben ist, beruht darauf, daß die Kraft eines
Theilchens, der Bewegung einer Flaͤche zu widerstehen, sich wie das Quadrat
des Sinus des Neigungs-Winkels dieser Flaͤche zur Richtung der Bewegung
verhaͤlt. Nun behaupte ich, daß dieß falsch ist, und daß das wahre
Verhaͤltniß des Widerstandes bloß einfach, wie der Sinus des Neigungs-Winkels ist.
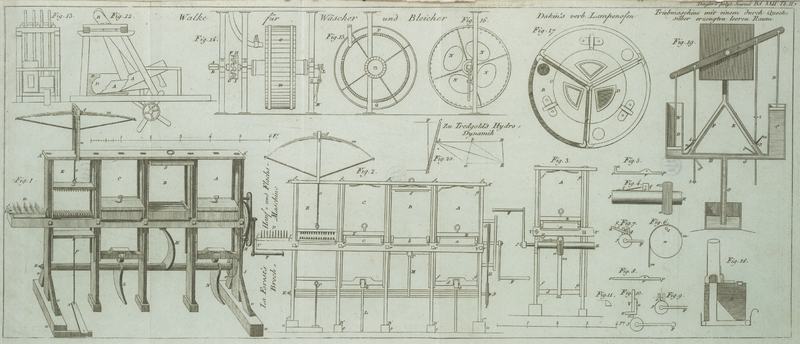
Denn: es sey, C, D, die Flaͤche, die sich mit
gleichfoͤrmiger Geschwindigkeit in der Richtung, A,
B, in einer stillstehenden Fluͤßigkeit bewegt; D, F, die Breite der sich bewegenden Flaͤche in
senkrechter Richtung auf die Richtung der Bewegung, und, C,
A, B, der Winkel, welchen die Flaͤche mit ihrer Richtung bildet.
Es sey, A, B, der unmittelbare Widerstand, welcher
noͤthig ist, um die Bewegung bei der gegebenen Geschwindigkeit
gleichfoͤrmig zu machen, und man ziehe, A, E,
senkrecht auf die Flaͤche, und, B, E, senkrecht
auf, A, B; so ist, A, E, der
senkrechte Druk auf die Oberflaͤche der Flaͤche, und der wirkliche
Druk der Fluͤßigkeit auf die Flaͤche muß sich zu dem wirklichen
Widerstande verhalten, wie, A, E, zu, A, B; folglich, da der wirkliche Druk einer
Fluͤßigkeit auf eine Flaͤche derselbe bleibt, wird der Widerstand wie,
A, B, d.h., wie der Sinus des Winkels, C, A, B, sich aͤndern.
Der Fehler in dem Beweise von Prop. 34. in den Principles besteht dann, daß man den Widerstand
eines Theilchens in einer, der Bewegung des Koͤrpers entgegengesezten
Richtung, fuͤr die ganze Wirkung nahm, waͤhrend, in Folge der
Continuitaͤt der Fluͤßigkeit, keine Zuruͤkstoßung Statt haben
kann, und der wirkliche Widerstand in senkrechter Richtung auf die
Oberflaͤche aus zwei Theilen zusammengesezt seyn muß: naͤmlich, aus
der Kraft in der Richtung der Bewegung, und aus der Kraft, durch welche der
Zuruͤkstoßung vorgebogen wird. Dieß fuͤhrt uns zu einem wichtigen
Lehrsaze bei diesen Untersuchungen.
Lehrsaz. Wenn eine ebene Flaͤche sich in einer
Fluͤßigkeit mit gleichfoͤrmiger Geschwindigkeit bewegt,
verhaͤlt sich die Hoͤhe einer Saͤule dieser Fluͤßigkeit,
welche diese Geschwindigkeit erzeugen wuͤrde, zu der Hoͤhe einer
Saͤule dieser Fluͤßigkeit, die dem Widerstande der Fluͤßigkeit
gleich ist, wie das Quadrat des Halbmessers zu dem doppelten Quadrate des Sinus des
Winkels der Flaͤche mit der Richtung ihrer Bewegung.
Der Widerstand ist wie, A, B; aber die Kraft der
Fluͤssigkeit ist wie, E, A; und wenn diese Kraft
zersezt wird, so erhalten wir ihre zwei Theile, A, b,
und, A, a, von welchen, A,
b, proportional ist der Hoͤhe einer Saͤule der
Fluͤßigkeit, welche der Geschwindigkeit der Bewegung der Flaͤche gehoͤrt, und, A, a, der Widerstand gegen die Zuruͤkstoßung.
Da aber der Winkel der Zuruͤkstoßung gleich ist dem Winkel des Einfalles, und
die Dreieke aͤhnlich sind, so ist
Rad.: Sin. CAB : : Ab : 1/2
AE.
Folglich AE = (2Ab
×
Sin. CAB)/Rad.
Ferner ist Rad.: Sin. CAB : : AE : AB; oder
AB = (2 Ab × Sin². CAB)/Rad.²
Folglich Ab : AB
: : Rad.² : 2
Sin.² CAB.
Wenn die Flaͤche in senkrechter Richtung auf ihre Oberflaͤche bewegt
wird, so wird Ab = AB/2, oder der Widerstand ist das doppelte Gewicht der Saͤule, die
der Geschwindigkeit angehoͤrt.
Diese Unterscheidung zwischen dem Widerstande, und der der Geschwindigkeit
angehoͤrigen Hoͤhe ist hoͤchst wichtig, und die Thatsache, daß
sie genau mit dem Resultate uͤbereinstimmt, welches man vorlaͤufig
erhielt, wenn die Bewegung senkrecht auf die Flaͤche ist, wird vielleicht der
hier aufgestellten hydraulischen Theorie einige Aufmerksamkeit gewinnen.
Die Vergleichung des Widerstandes eines Cylinders und einer Kugel verlangt noch eine
weitere Untersuchung, indem die Bewegung der Flaͤche, und der darauf folgende
Druk in Betracht gezogen werden muß. Wenn wir diese beiden vernachlaͤßigen,
oder bloß den unmittelbaren Widerstand einer Kugel und eines Cylinders von gleichem
Durchmesser vergleichen, so wird das Verhaͤltniß, wie 2 : 3, nicht wie 1 : 2
seyn.
Tafeln