| Titel: | Ueber praktische Verfertigung achromatischer Objectiv-Gläser. Von Peter Barlow, Esqu., F. R. S., und Prof. an der k. Militär-Akademie zu Woolwich. |
| Fundstelle: | Band 23, Jahrgang 1827, Nr. I., S. 2 |
| Download: | XML |
I.
Ueber praktische Verfertigung achromatischer
Objectiv-Glaͤser. Von Peter Barlow, Esqu., F. R. S., und Prof. an der
k. Militaͤr-Akademie zu Woolwich.
Aus dem Edinburgh Philosophical Journal. N. 27. S. 1.
N. 28. S. 311.
Mit Abbildungen auf Tab.
I.
Barlow, uͤber praktische Verfertigung achromatischer
Objectiv-Glaͤser.
1)
Die Mathematiker haben eine Menge verschiedener Methode
vorgeschlagen, um die Brechnungs- und Zerstreuungs-Kraft des Glases zu
bestimmen, und verschiedene Regeln zur Berechnung der Halbmesser der
Kruͤmmung der Linsen gegeben, die das Objectiv-Glas unserer
achromatischen Fernroͤhre bilden. Die theoretischen Optiker verstehen diesen
Gegenstand vielleicht so genau, als man nur immer wuͤnschen kann; allein,
dieß ist nicht der Fall bei allen, die sich praktisch mit
Objectiv-Glaͤsern beschaͤftigen: fuͤr Leztere ist dieser
Aufsaz geschrieben. Er soll nicht neues Licht uͤber diesen hoͤchst
interessanten Gegenstand verbreiten, sondern bloß Alles, unter einem Gesichtspuncte
zusammenfassen, und auf die einfachste Form zuruͤkfuͤhren, was dem
praktischen Optiker wirklich nothwendig ist, naͤmlich:
1. Den Brechungs-Index seiner beiden Glaͤser auf das Genaueste zu
bestimmen:
2. die verhaͤltnißmaͤßige Zerstreuungs-Kraft derselben zu
bestimmen:
3. die Halbmesser der Kruͤmmung der verschiedenen Flaͤchen so zu
bestimmen, daß sie die achromatische Eigenschaft mit der geringsten
sphaͤrischen Abweichung erzeugen.
In Hinsicht auf die erstere dieser Bestimmungen wurde das von Biot, in seinem Traité de Physique
empfohlene und beschriebene Instrument angenommen, so wie die von demselben
gegebenen Berechnungs-Regeln: leztere wurden jedoch in eine fuͤr die
meisten Leser verstaͤndlichere Sprache eingekleidet.
Zur Bestimmung der Zerstreuungs-Kraft wurde das von
Dr. Brewster erfundene, und von ihm in seinem „Treatise on New Philosophical Instruments“ beschriebene Instrument als das einfachste, und zu jeder praktischen Anwendung
vollkommen hinreichende ausgewaͤhlt; zur Berechnung fuͤr diesen Fall
wurden die von Boscovich angegebenen, und in dem lezt
erwaͤhnten Werke angefuͤhrten, Formeln nach einiger Vergleichung den
uͤbrigen vorgezogen.
Zur Berechnung der Kruͤmmungen haben wir die von Hrn. Herschel in den Philosophical Transactions so
trefflich erlaͤuterten Regeln, die vor allen anderen entschiedene
Vorzuͤge besizen, angenommen, und seine Tabellen noch weiter ausgedehnt, um
die Muͤhe der weiteren Berechnung so viel nur immer moͤglich zu
ersparen.
Fuͤr jeden Fall wurden wirkliche Beobachtungen und Berechnungen
hinlaͤnglich im Detail aufgefuͤhrt, um sie jedem verstaͤndlich
zu machen, der auch nur die ersten Grundsaͤze der Mathematik inne hat, wenn
er in den Fall kommen sollte, aus Flint- und Tafel- oder
Kronen-Glas, dessen Eigenschaften er noch nicht kennt, ein
Objectiv-Glas von irgend einer gegebenen Brennweite zu verfertigen.
2. Instrument zur Messung der Winkel der
Prismen und zur Bestimmung des Refractiv-Index.
Das Erste, was der Kuͤnstler zum thun hat, ist, daß er sich zwei kleine
Prismen aus dem Flint- und Kronen-Glase verfertigt, welches er
zugleich anzuwenden gedenkt, und sie auf einen Winkel von ungefaͤhr
30° bringt: die genauere Messung dieser Winkel muß in der Folge mittelst des
unten beschriebenen Instrumentes geschehen.
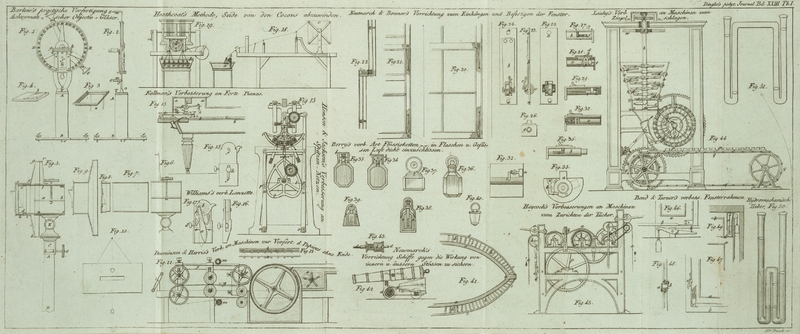
Dieses Instrument zeigen Fig. 1 und 2. Tab. 1. im Aufrisse.
s, s, s, sind drei Schrauben, die als Fuͤße
des Instrumentes, und zur senkrechten Aufstellung desselben dienen. A, B, ist eine Roͤhre, welche auf den drei Armen,
die die Basis des Instrumentes bilden, befestigt ist. T,
ist eine innere Roͤhre, die sich in der vorigen schiebt, und wodurch das
Instrument in jede beliebige Lage gebracht werden kann. C, ist eine Art Armes, der auf der inneren Roͤhre befestigt ist,
und auf welchen der Hauptkreis aufgeschraubt wird, der, wie die Figur zeigt, in
Grade getheilt ist. m, m, sind zwei Arme, die sich um
einen gemeinschaftlichen Mittelpunct drehen, der zugleich der Mittelpunkt des
Kreises ist: an jedem Arme ist an dem Ende desselben eine Scheibe angebracht, welche mit einer
stellbaren Diopter mit einem sehr feinen Loche versehen ist. ef, ist eine, durch eine in Fig. 2. gezeichnete
Tangenten-Schraube stellbare, Messing-Platte, welche an ihrem oberen
Theile einem vierekigen Rahmen fuͤhrt, der unter einem rechten Winkel darauf
befestigt ist. Dieser vierekige Rahmen ist innenwendig ausgefalzt, so daß er eine
Glasplatte parallel aufnimmt, auf welche das Prisma zur Beobachtung gelegt wird, wie
man in beiden Figuren sieht.
Den Bau dieses Rahmens wird man aus der perspectivischen Zeichnung in Fig. 3. besser einsehen.
Fig. 4.
ist eine parallel geschliffene Messingplatte, die sich genau uͤber den Rahmen
schiebt, so daß die gerade eingeschnittene Kante, a, b,
genau dem Mittelpuncte des in Grade getheilten Kreises gegenuͤber zu stehen
kommt, und das Prisma, wenn es auf die Glasplatte gebracht wird, genau mit dieser
Kante in Beruͤhrung kommt. Die oben erwaͤhnte
Tangenten-Schraube dient, den Rahmen auf- oder abwaͤrts zu
stellen, bis die Kante, a, b, der Platte dem
Mittelpuncte, wie oben angegeben wurde, gegenuͤber zu stehen kommt.
3. Messung des Winkels des
Prisma.
Hierzu ist es am besten, sich des parallelen am Ruͤken geschwaͤrzten
Glases zu bedienen, oder ein Glas hierzu besonders aufzubewahren. Dieses Glas legt
man in Rahmen, und stellt das Instrument mittelst einer kurzen darauf gestellten
Weingeist-Wasserwage und der Schrauben, die die Fuͤße desselben
bilden, vollkommen horizontal, worauf man die Messingplatte einschiebt, die
gleichfalls geschwaͤrzt seyn muß, um alle Verwirrung durch
zuruͤkgeworfenes Licht zu vermeiden. Nun bringt man beide Arme uͤber
die horizontale Linie, oder 0, und stellt sie beide mittelst des Verniers auf
denselben Winkel, z. B. 40° oder 50°. etc. Wenn man nun durch eines
der kleinen Loͤcher in den Dioptern sieht, so muß die Zuruͤkwerfung
des anderen von der Kante der Messingplatte in der Mitte getheilt werden, und, wo
dieß nicht der Fall waͤre, muͤssen die Dioptern so gestellt werden,
daß dieß geschieht. Hierauf legt man das Prisma auf, und bringt seine scharfe Kante
sanft gegen die oben erwaͤhnte Kante der Platte, und richtet die eine
Diopter, waͤhrend die andere unbewegt feststehen bleibt, so lang, bis die
Zuruͤkwerfung des kleinen Loches der lezteren durch die gerade Kante, wie vorher, in der Mitte
getheilt erscheint, und dann gibt die Differenz in den angezeigten Graden den
gesuchten Winkel. Diese hoͤchst einfache Operation kann bei mehreren Winkeln
wiederholt, und dann die Mittelzahl fuͤr den Winkel des Prisma genommen
werden.
4. Folgende Beispiele werden diese Operation hinlaͤnglich
erlaͤutern.
Flint-Prisma, N. 1.
Feststehende Diopter.
Bewegliche Diopter.
Unterschied.
Halber Unterschied oder Winkel.
40° 0'
89° 38'
49° 38'
24° 49'
30 0
79 36
49 36
24 48
35 0
84 40
49 40
24 50
36 0
85 38
49 38
24 49
25 0
74 38
49 38
24 49
Mittlerer Winkel
24 49
Tafel-Glas-Prisma, N. 1.
Feststehende Diopter.
Bewegliche Diopter.
Unterschied.
Halber Unterschied oder Winkel.
40° 0'
89° 42'
49° 42'
24° 51'
35 0
84 40
49 40
24 50
30 0
79 44
49 44
24 52
25 0
74 44
49 44
24 52
20 0
69 40
49 40
24 50
Mittlerer Winkel
24 51
Der Grundsaz dieser Ableitung ist zu einleuchtend, als daß er einer weiteren
Erlaͤuterung beduͤrfte; man braucht bloß zu bemerken, daß er sich auf
das bekannte Gesez gruͤndet, daß der Einfalls-Winkel dem
Zuruͤkwerfungs-Winkel gleich ist.
5. Beobachtungen zur Bestimmung des
Index der Brechung.
Es ist ein bekannter Grundsaz in der Optik, daß, waͤhrend des Durchganges des
Lichtes aus einem Mittel in das andere, z.B., aus Glas in die Luft, die Sinus der
Einfalls- und Brechungs-Winkel in einem staͤten
Verhaͤltnisse sind. Dieses Verhaͤltniß heißt der Index der Brechung.
Um die nothwendigen Daten zur Bestimmung dieses Index zu erhalten, muß auf folgende
Weise verfahren werden:
Nachdem das Instrument, wie oben, gestellt wurde, bringt man die reine parallele
Glasplatte, statt der schwarzen, deren man sich in dem vorigen Falle bediente, in
den Rahmen, wendet die geschwaͤrzte Messingplatte an, und bringt eben so die
Kante des Prisma in Beruͤhrung mit der Kante der Platte, wie oben.
Die Dioptern werden nun so gestellt, wie in Fig. 1. Tab. I
naͤmlich die eine gegen die Kante des Prisma, uͤber 0 oder
uͤber die Horizontale, und die andere gegen die Basis unter derselben, je
niedriger desto besser, und auf denselben Grad, z.B. 60 oder 55°.
Man legt auf den Tisch, unter die untere Diopter, ein Stuͤk reines weißes
Papier, und laͤßt darauf, wenn es nothwendig ist, ein starkes Licht, am
besten Sonnenlicht, fallen. Dann bewegt man die obere Diopter so lange, bis das Auge
das zuruͤkgeworfene Bild der unteren Diopter durch die gerade Kante in der
Mitte getheilt sieht, und merkt den Grad an. Dieß sind alle Daten, die nothwendig
sind, um die Rechnung zu beginnen; groͤßerer Sicherheit wegen wird es aber am
besten seyn, die Beobachtung unter drei bis vier verschiedenen
Einfalls-Winkeln zu wiederholen.
Das Bild wird, bei diesem Versuche, gefaͤrbt und lang gezogen erscheinen; es
wird aber, bei einiger Uebung, nicht schwer werden, dasselbe in der Mitte zu
theilen.
Anmerkung.
Zur Vermeidung aller Verwirrung in der Rechnung, die durch die Zeichen der
Cosinus uͤber und unter 90° entstehen, wird es am besten seyn, die
Supplemente der gefundenen Grade, oder das, was zu 180° noch fehlt, statt
der Grade selbst zu nehmen.
6. Ein Paar Beobachtungen uͤber
obige Prismen.
Flint-Prisma, N. 1.
No.
Supplement zudem Grade desunteren
Index. (Q)
Supplement zudem Grade desoberen
Index. (P)
Haͤlfte
desUnterschiedes. (d)
Oben gefundenerWinkel des
Prisma (a)
1234
120°
0' 125 0 130 0 135 0
104°
10' 108 45 113 0 117 10
7°
55' 8 7 8 30 8 55
24° 49'
Tafelglas-Prisma. N. 1.
No.
Supplement zudem Grade desunteren Index.
Supplement zudem Grade desoberen Index.
Haͤlfte desUnterschiedes.
Oben gefundenerWinkel des Prisma
1234
120°
0' 125 0 130 0 135 0
106° 0' 110 38 115 0 119 40
7° 0' 7 11 7 30 7 40
24° 51'
Es sey der Winkel
in der ersten Spalte
= Q;
in der zweiten –
= P;
in der dritten –
= d,
oder der Haͤlfte d. Unterschiedes;
in der vierten –
= a,
oder dem Winkel des Prisma;
so laͤßt sich die Regel zur Berechnung des Index in
Worten auf folgende Weise ausdruͤken:
7. Regel zur Berechnung des Index der
Brechung.
1. Man addire zu dem Winkel P, den Winkel d, und subtrahire von der Summe 1/2 a: der Rest sey = A.
2. Man addire 1/2 a und d
zusammen: die Summe sey = B.
3. Man addire Cotangente 1/2 a,In allen diesen Faͤllen ist der Logarithmus zu verstehen. A. d. O. Tangente A und Tangente B zusammen, ziehe 20 von der Summe ab, und finde den Winkel, dessen
Tangente der Rest ist: er sey = D.
4. Von D ziehe man 1/2 a ab;
der Rest sey = E.Wenn in irgend einem Falle der Winkel A weniger,
dann 90° waͤre, muß man, statt des gefundenen Winkels D, ein Supplement, oder was an 180° noch
fehlt, nehmen, wenn man E finden will. A. d.
O.
5. Von Cosin. Q ziehe man Cosin. E ab, und finde die natuͤrliche Zahl, die dem Reste als Logarithmus
entspricht: diese wird der gesuchte Index seyn.Der algebraische Ausdruk fuͤr diese Regel, der denjenigen, die sich
mit Analysis beschaͤftigen, gelaͤufiger seyn wird, kann auf
folgende Weise ausgedruͤkt werden:Tang. D = Cotang.
1/2 a Tang. (P + d – 1/2 a)
Tang. (d + 1/2
a)Index r = Cosin.Q/Cosin.(D –
1/2 a).Siehe Biot
Traité de Physique. A. d. O.
Rechnung.
Flint-Prisma.
Erste Beobachtung.
Zu P
=
104° 10'
Zu 1/2 a
=
12° 24' 1/2
Addire d
=
7 55
Addire d
=
7 55
––––––––––
–––––––
Von der Summe
=
112 5
Summe B
=
20 19
Ziehe ab 1/2 a
=
12 24 1/2
––––––––––
A
=
99° 41'
Cotangente 1/2 a
=
12° 24' –
10,6578454
Tang. A
=
99 61,oder89 19
10,7679350
Tang. B
=
20 19
9,5684856
–––––––––––
Tang. 84° 13'
=
D
10,9942660
Von D
=
84° 13
Ziehe ab 1/2 a
=
12 24
––––––
E
=
71 49
Von Cosin. Q
=
120°, oder 60
9,6989700
Ziehe ab Cos. E
=
71° 49 –
9,4942361
Natuͤrliche Zahl
=
1,6019 Index
0,2046339.
8.
Rechnung.
Flint-Prisma.
Zweite Beobachtung.
Zu P
=
108° 45'
Zu 1/2 a
=
12° 24
Addire d
=
8 7
Addire d
=
8 7
–––––––
––––––
Von Summe
116° 52'
Summe B
=
20 31
Subtrahire 1/2 a
12 24 1/2
–––––––
A
=
104 27
Contag. 1/2 a
= 12° 24'
10,6578454
Tang. A
=
104 27 75 31
oder
10,5889079
Tang. B
= 20 31
9,5731227
–––––––––
30,8198760
Subtrahire
20,0000000
–––––––––
Tang. 81° 23'
= D
. . . . . . . .
10,8198760
Von
D
= 81° 23'
Subtr.
1/2
a
= 12 24
––––––––
E
= 68 59
Von Cosin. Q
=
125° 0' oder 55 0
9,7585913
Ziehe ab Cos. E
=
68 59
9,5546581
–––––––––
Natuͤrliche Zahl
=
1,5993 Index
0,2039332
Dieser Index ist von dem vorigen um 0,0026 verschieden, und wurde hier als Beispiel
einer außerordentlichen Abweichung gegeben: ein groͤßerer Unterschied darf
nie gestattet werden; sollte er jemahls diese Groͤße uͤbersteigen, so muß die Beobachtung
wiederholt werden. Bei einer großen Zahl solcher Versuche fand ich allgemein
vollkommene Uebereinstimmung in den drei ersten Decimalen.
Die
dritte
Reihe
von
Beobachtungen
gibt
den
Index
=
1, 6013
vierte
–
–
–
–
–
–
=
1,5994
erste
–
–
–
–
–
–
=
1,6019
zweite
–
–
–
–
–
–
=
1,5993
–––––
––––––
4)
6,4019
–––––
––––––
Mittlerer
Index
1,6005
Aehnliche Rechnungen geben fuͤr das Tafelglas-Prisma, als mittleren
Index r = 1,5279.
9. Instrument zur Messung der
Zerstreuung, und zur Bestimmung des
Zerstreuungs-Verhaͤltnisses.
Es ist eine in der Optik allgemein bekannte Thatsache, daß Licht, wenn es aus einem
Mittel in das andere uͤbergeht, nicht bloß gebrochen, sondern auch in
verschieden gefaͤrbte Lichtstrahlen zersezt wird, und dadurch das sogenannte
Spectrum bildet; daß der aͤußerste Strahl, der rothe, derjenige ist, der an.,
wenigsten, und der violette, der aͤußerste an dem anderen Ende derjenige, der
am meisten gebrochen wurde. Die Brechungs-Index fuͤr diese beiden
Strahlen such also verschieden, und der Unterschied zwischen denselben, getheilt
durch den mittleren Index Weniger 1, ist das Zerstreuungs-Verhaͤltniß, (Dispersive Ratio), und das Verhaͤltniß zwischen
dem Zerstreuungs-Verhaͤltnisse zweier verschiedener Glaͤser ist
das Verhaͤltniß der zerstreuenden Kraͤfte,
oder Zerstreu-Verhaͤltniß (Ratio of Dispersion). Man nennt lezteres jedoch auch
oͤfters Zerstreuungs-Verhaͤltniß
zweier Glaͤser.
Das Instrument zur Bestimmung dieses Verhaͤltnisses ist folgendes:
A, B, Fig. 5. ist eine
messingene Saͤule, auf welche oben die Kappe, C,
paßt, die mit einem Gewinde, k, versehen ist: oben auf
demselben befindet sich eine kurze Roͤhre, l, m, n,
o, die an der Seite, a, b, offen ist, und eine
Stellschraube, s, hat. In dieser kurzen Roͤhre
ist eine andere Roͤhre eingefuͤgt, die doppelt so lang ist, und die,
wenn sie in gehoͤrige Stellung gebracht wurde, durch die Stellschraube, s, die die aͤußere Roͤhre darauf sperrt,
in dieser Lage festgehalten werden kann. Diese Roͤhre ragt bis zur Linie, c, d, vor, die das Ende derselben zeigt, e, f, h,
i, ist eine andere Roͤhre, die sich uͤber c, d, schiebt, und an ihrem Ende, f, i, die kreisfoͤrmige Platte, g, h,
fuͤhrt, die an ihrer aͤußeren Kante zu beiden Seiten von 0 bis auf
180° getheilt ist. r, ist ein, an der ersten
aͤußersten Roͤhre, l, m, n, o,
angebrachter Vernier. Der Durchmesser dieser Roͤhren kann ungefaͤhr 2
1/2 Zoll betragen. Das Ende der Roͤhre, e, f, h,
i, hat einen Ansaz oder eine Basis bei e, h, in
welcher sich ein kreisfoͤrmiges Loch von ungefaͤhr 1 1/2 Zoll im
Durchmesser befindet, und eine Vorrichtung, ein Prisma darauf zu befestigen, wie man
in der Figur sieht. Die Roͤhre, c, d, endet sich
bei c, d, gleichfalls in eine aͤhnliche Basis zu
demselben Zweke, laͤßt sich aber, wie eine gewoͤhnliche Scheidewand,
ein- und ausschieden, damit man das Prisma innenwendig anbringen kann, und
die beiden inneren Flaͤchen der beiden Prismen parallel zu stehen kommen.
Der Bau dieses Instrumentes wird durch die Figuren 6, 7, 8, 9, 10 deutlicher, wo Fig. 6. die
Roͤhre darstellt, die das Gehaͤuse auf der Saͤule bildet, sammt
ihrem Vernier und der Stellschraube. Fig. 7. ist die
Roͤhre, die in dieselbe zunaͤchst eingeschoben wird. Fig. 8. ist die
Scheidewand, die das Prisma fuͤhrt, welches in Fig. 7. eingefuͤgt
wird. Fig. 9.
ist eine kurze Roͤhre mit einem in Grade getheilten Kreise, die uͤber
Fig. 7.
anschließt, und gleichfalls ein Prisma fuͤhrt, wie man in Fig. 5. sieht, wo alle
diese Roͤhren an ihrer Stelle sind.
Nachdem dieses Instrument so vorgerichtet wurde, versieht man sich mit einem glatten
Brette von ungefaͤhr 2 Fuß im Gevierte, welches mit Lampen-Schwarz
gehoͤrig geschwaͤrzt ist, und strekt quer uͤber dasselbe einen
gleich breiten Streif von sehr weißem reinen Kartenpapiere. Dieses Brett wird, mit
dem Kartenpapiere horizontal, in starkes Licht senkrecht aufgehaͤngt, so daß
das Senkloth das Papier in der Mitte durchschneidet, wie in Fig. 10. Dann stellt man
das Zerstreuungs-Instrument in einer Entfernung von ungefaͤhr 6 bis 8
Fuß vorne vor demselben auf, und alles ist somit zur Beobachtung vorgerichtet.
10. Verfahren bei der
Beobachtung.
1. Man nimmt die Roͤhre und den in Grade getheilten Kreis, Fig. 9. mit seinem Prisma
ab, welches immer dasjenige seyn muß, das die groͤßte
Zerstreuungs-Kraft besizt, und dreht die Roͤhre Fig. 7. in der
Roͤhre Fig.
6. so lang um, bis die Kante des am Ende derselben befestigten Prisma nach
aufwaͤrts
gekehrt, und vellkommen horizontal ist, was man baran erkennt, daß das Auge die
Linie des Senklothes gerade uͤber der Kante des Prisma, und das gebrochene
Bild desselben in dem Prisma in Einer senkrechten Linie gewahr wird. Zu diesem Ende
ist auch oben uͤber dem Prisma vorne an der Scheidewand ein Raum gelassen.
Nachdem dieß geschehen ist, befestigt man es in dieser Lage mittelst einer
Stellschraube. Man nimmt nun das Senkloth weg, und sieht auf den
Kartenpapier-Streif, dessen oberer Rand stark violett und blau
gefaͤrbt seyn wird, waͤhrend der untere roth und gelb ist. Nun stekt
man die Roͤhre, Fig. 9. mit dem Prisma an,
und bringt die Basis desselben aufwaͤrts und horizontal, und wird dann, wenn
man den Streif Kartenpapier wieder betrachtet, (denn dieses leztere Prisma hat immer
eine groͤßere Zerstreuungs-Kraft), den oberen Rand roth und gelb, und
den unteren violett finden. Wenn nun Fig. 9. allmaͤhlig
entweder rechts oder links gedreht wird, waͤhrend das Auge immer auf den
Streif Kartenpapier gerichtet bleibt, werden die Farben an beiden Baͤndern
desselben immer schwaͤcher werden, und endlich bei einer gewissen Lage
gaͤnzlich verschwinden. Nachdem man dieß genau und sorgfaͤltig
beobachtet hat, schreibt man den Grad, den der Vernier an dem in Grade getheilten
Kreise zeigt, auf. Dann dreht man den Kreis in der anderen Richtung um, bis die
Farben wieder verschwinden, und bemerkt, wie vor, den Grad am Vernier. Der halbe
eingeschlossene Bogen zwischen den beiden bemerkten Graden ist M. (Dieß ist die Differenz zwischen den Graden, wenn
beide auf derselben Seite sind; aber die Summe, wenn sie auf verschiedenen Seiten
liegen.)
Diese sehr einfache Beobachtung wiederholt man mehrere Mahle, und das Mittel aus
allen Resultaten gibt M.
11. Berechnung des
Zerstreu-Verhaͤltnisses.
1. Das in Fig.
8. befestigte Prisma, oder das feststehende Prisma, welches wir hier aus
Tafelglas annehmen, sey A, welches auch den Winkel
desselben andeutet: das Flint-Prisma in Fig. 9., so wie der Winkel
desselben, sey B. Nun
2. Addire man zu dem Logarithmus des Sinus A, den
Logarithmus seines Brechungs: Index, und ziehe von der Summe den Logarithmus des
Brechungs-Index des Winkels B, ab, und finde den
Winkel, von welchem der Rest der Logarithmus des Sinus ist: dieser Winkel sey = a.
3. Zu dem Logarithmus der Tangente des Winkels, B, addire
man den Logarithmus des Cosinns des Winkels, M, und
finde den Winkel, von welchen die Summe der Logarithmus der. Tangente ist. Dieser
Winkel sey = b.
4. Von a ziehe man b ab, und
nenne den Rest = c.
5. Von dem Logarithmus der Tangente von c, ziehe man den
Logarithmus der Tangente von a ab, betrachte den Rest
als Logarithmus, und finde die natuͤrliche Zahl desselben, welche man von der
Einheit abziehen muß.
6. Multiplicire man diesen Rest mit dem Brechungs-Index des Prisma A, und mit dem Index – 1 (oder dem zehnten Theile
des Index) des Prisma B. Man multiplicire auch den
Brechungs-Index von B mit dem zehnten Theile des
Index von A. Zulezt theile man das erstere Product durch
das leztere: der Quotient ist das Zerstreu-Verhaͤltniß der beiden
Glaͤser.
Oder: man addire die Logarithmen der drei ersten Zahlen zusammen, und die der beiden
lezteren: die Differenz, welche man erhaͤlt wenn man leztere von ersterer
abzieht, ist der Logarithmus des gesuchten Verhaͤltnisses.Der analytische Ausdruk fuͤr diese Regel ist:Sin. a (r. Sin.
A)/R Tang. b Cosin. M Tang. B = Tang. b.Zerstreuungs-Verhaͤltniß = r(R – 1)/R(R – 1) {Tang. (b – a) Cotang. a +
1} wo r der Brechungs-Index von
A, und R jener
von B ist. A. d. O.
Anmerkung.
Man hat bei obiger Regel angenommen, daß das Prisma B, seine hoͤhere Zerstreuung seiner hoͤheren
Zerstreuungs-Kraft verdankt, da die Winkel beinahe gleich sind; aber bei
geringerer Zerstreuungs-Kraft wird, wo ein groͤßerer Winkel
vorhanden ist, seine Zerstreuung immer groͤßer seyn, als die des Prisma
A. In diesem Falle gilt jedoch dieselbe Regel,
nur mit dem Unterschiede, daß man oben (5) die natuͤrliche Zahl zu der
Einheit addiren, statt von derselben subtrahiren muß, wovon der Grund aus der
algebraischen Formel erhellt.
12. Beispiel.
welches die Resultate der Beobachtung und Berechnung an den
beiden Prismen aus Tafelglas N. 1, und Flintglas N. 1 darstellt, deren Winkel und Index wir bereits
bestimmt haben, naͤmlich:
Winkel
des
Tafelglas-Prisma
A = 24°. 51.
Index = 1,528.Drei Decimal-Stellen reichen vollkommen hin, und wir
haben diese bis zur naͤchsten Zahl genommen: beide aber etwas
groͤßer. A. d. O.
–
–
Flintglas-Prisma
B =
24, 49.
Index = 1,601.
Beobachtung zur Bestimmung des WinkelsM.
Grade, wo der Zeigerrechts gedreht
wurde, bis die Farben
verschwanden
5°
10 5 16 5 30 5 10 5 16
Grade, wo der
Zeiger
links gedreht
wurde
117° 44'
117 54117 30
117 44117 40
––––––
–––––––
5)
25 92
5)
558 32
––––––
–––––––
Mittel
5 18
Mittel
117 42
5 18
–––––––
2)
112 24
–––––––
Winkel
M
= 56 12
Nun, nach der Regel, zu
Sin. A = Sin.
24° 51'
= 9,6235016
Zu Tang.
B = 24° 29'
= 9,6650346
Addirt Log. 1,528
= 0,1841234
Add. Cos. M = 56° 12'
= 9,7453056
–––––––––––
–––––––––––
9,8076250.
Tang. 14° 25' = b
= 9,4103402.
Subtrahirt Log. 1,601
0,2043913
–––––––––
Sin. 23° 39' = a
9,6032337
Von Winkel
a
= 23° 39'
Subtrahirt
Winkel b
= 14 25
––––––––
Winkel c
= 9° 14'
Von
Tangente c
= 9° 14
= 9,2110184
Abgezog.
Tangente a
= 23 39
= 9,6414036
–––––––––––
1,5696148
Natuͤrliche Zahl =
0,37121
Von
1,00000
Abgezogen
0,37121
––––––––
Rest
0,62879
Logarithmus des Restes
0,62879
=
1,7985056
Logarith. des Index von A
1,528
=
0,1841234
Logarith. 1/10 Index v. B
0,601
=
1,7788745
–––––––––
Erste Summe
1,7615035
Logarith. des Index B = 1,601
=
0,2043913
Logarith. 1/10 Index A = 0,528
=
1,7226339
–––––––––
Zweite Summe
1,9270252
Von
1,7615035
Abgezogen
1,9270252
–––––––––
Natuͤrliche
Zahl 0,68309
=
1,8344783
Also ist das Verhaͤltniß der Zerstreuungs-Kraͤfte der beiden
Glaͤser, wie 1 : 0,68309, oder, wie man sich gewoͤhnlich
ausdruͤkt, 0,68309.
Auf diese Weise haben wir die nothwendigen Daten zur Bestimmung der
Kruͤmmungs-Halbmesser, die den Linsen aus Tafel-, und
Flint:Glas gegeben werden muͤssen, um ein achromatisches Objectiv-Glas
zu bilden.
13. Rechnungs-Tafeln etc. zur
Bestimmung der Kruͤmmungs-Halbmesser, wenn der
Brechungs-Index eines jeden Glases und das
Zerstreuungs-Verhaͤltniß gegeben ist.
Wenn es nun bloß noͤthig waͤre, das Objectiv-Glas in Hinsicht
auf Farbe oder Zerstreuung der Lichtstrahlen zu verbessern, so brauchte es nichts
weiter, als die Brennweiten der beiden Linsen in geradem Verhaͤltnisse ihrer
Zerstreuungs-Kraͤfte zu bilden: bei drei (unter gewissen
Graͤnzen) nach Belieben gebildeten Oberflaͤchen koͤnnte die
vierte immer so eingerichtet werden, daß sie die Farbe verbessert: dieß ist auch
das, was einige Optiker noch immer thun. Verbesserung der Farbe ist aber durchaus
nicht Alles, was zur Verfertigung eines Objectiv-Glases fuͤr ein gutes
Fernrohr gehoͤrt: denn, wenn man nicht auch auf die sphaͤrische
Abweichung Ruͤksicht nimmt, wird das Bild, obschon frei von aller
Faͤrbung, in einem nebeligen und rauchigen Felde erscheinen, und dadurch sehr
unvollkommen und undeutlich werden.
In Bezug auf. diese lezte Verbesserung hat Hr. Herschel
einen sehr schaͤzbaren und trefflich ausgearbeiteten Aufsaz mit Tabellen in
den Philosophical Transactions of the roy. Society Part.
II. 1821 geliefert, wodurch die Muͤhe der Berechnung um ein Bedeutendes
erspart wird. Indem wir diese Tabellen weiter ausdehnten, glaubten wir unser
Scherstein zur Vereinfachung dieser wichtigen, und ohne solche Huͤlfsmittel
muͤhevollen und verwikelten Rechnung beigetragen zu haben. Ehe wir zu einer
Erklaͤrung dieses Verfahrens uͤbergehen, wollen wir, in deutlichen
Worten, einige vorlaͤufige Regeln zur Bestimmung der Brennweiten einfacher
Linsen vortragen, deren Brechungs-Kraft und Halbmesser der Kruͤmung
gegeben sind, und umgekehrt: denn, obschon diese Regeln, in einer Form oder in der
anderen, praktischen Optikern bekannt seyn moͤgen, so wird man uns doch
entschuldigen, wenn wir sie in Kuͤrze hier anfuͤhren, indem wir wuͤnschen, daß dieser
Aufsaz alle Regeln enthalte, die zur Verfertigung eines guten Objectiv-Glases
nothwendig sind.
14. Regeln zur Bestimmung der Brennweite
der Linsen von einer gegebenen Kruͤmmung.Die algebraische Formel, die alle diese Regeln umfaßt, ist folgende,
naͤmlich:fuͤr parallele Strahlen, f = rR/[a(r + R)], (Siehe Encyclopedia Metropolitana. Art. Optics
) wo f die Brennweite, a ein Zehntel Brechungs-Index, und r und R die
Halbmesser, die beide positiv sind, wenn beide Flaͤchen convex, und
negativ, wenn beide concav sind. A. d. O.
1) Die Brennweite einer doppelt convexen Linse fuͤr
parallele Strahlen zu finden, wenn die Halbmesser der Kruͤmmung und der
Brechungs-Index gegeben sind.
Regel. Man multiplicire die beiden Halbmesser mit
einander; addire hierauf beide und multiplicire die Summe derselben mit einem
Zehntel des Brechungs-Index. Das erste Product, getheilt durch das lezte,
wird die Brennweite seyn.
Beispiel. Die Kruͤmmungs-Halbmesser einer
Flint-Linse seyen 4 Zoll und 10 Zoll, und ihr Brechungs-Index 1,601:
man finde die Brennweite.
Textabbildung Bd. 23, S. 14
2) Wenn die beiden Halbmesser gleich sind, wird die Regel
einfacher, wie folgt:
Man theile den Halbmesser der Kruͤmmung durch zwei Zehntel des Index, so
erhaͤlt man die Brennweite.
Beispiel. Der Halbmesser der beiden gleichen
Oberflaͤchen der Flint-Linse (deren Index 1600 ist), sey = 10 Zoll:
man finde die Brennweite
Hier wird
0,600
2
–––––
1,200) 10,000 (8,33 Brennweite.
Beide diese Regeln gelten auch, wenn beide Oberflaͤchen concav sind; nur muß
dann das Resultat negativ genommen werden.
3) Die Brennweiten an einer plan-convexen Linse
fuͤr parallele Strahlen zu bestimmen, wenn der Halbmesser der convexen Seite
und der Index gegeben ist.
Regel. Man theile den Halbmesser der Kruͤmmung
durch ein Zehntel des Brechungs-Index; der Quotient wird die Brennweite
seyn.
Beispiel. Man verlangt die Brennweite einer planconvexen
Linse aus Kronenglas, deren Kruͤmmungs-Halbmesser 12 1/3 Zoll, und
Brechungs-Index 1,520 ist.
12 1/2 = 12,5.
0,52) 12,50 (24,04 Brennweite.
4) Die Brennweiten einer Linse mit einer concaven und einer
convexen Flaͤche zu bestimmen, wenn die Halbmesser, und der
Brechungs-Index gegeben, und die Strahlen parallel sind.
Regel. Man multiplicire die beiden Halbmesser mit
einander, man multiplicire auch ihre Differenz mit 1/10 des Brechungs-Index;
das erste Product durch das leztere getheilt gibt die Brennweite, die positiv seyn
wird, wenn der Halbmesser der concaven Flaͤche der groͤßere von beiden
ist, und negativ, wenn er der kleinere ist.
Beispiel. Man finde die Brennweite einer Linse aus
Flintglas, wo der Halbmesser der convexen Seite 10 Zoll, der der concaven Seite 16
Zoll, der Brechungs-Index 1,600 ist.
Hier wird
10
16
16
10
–––
––
Erstes Product
160
Differenz
6
0,600
–––––––
Zweites Product
3,6) 160 (44,44 Brennweite.
Das Resultat ist hier positiv; waͤre aber die convexe Seite 16, die concave
10, so wuͤrde die Brennweite dieselbe gewesen seyn, die Strahlen
wuͤrden aber divergirt haben, oder das Resultat waͤre negativ.
5) Aus der gegebenen Brennweite einer doppelt convexen oder
planconvexen Linse, und der negativen Brennweite einer doppelt concaven Linse oder
einer concav-convexen Linse die Brennweite des daraus zusammengesezten
Objectiv-Glases zu finden.
Regel. Man multiplicire die beiden Brennweiten mit
einander; theile das Product durch ihre Differenz: der Quotient wird die Brennweite
des zusammengesezten Objectiv-Glases.
Anmerkung
Wenn die negative Brennweite die kleinere ist, wird die daraus hervorgehende
Brennweite immer negativ seyn; wenn sie aber groͤßer ist, wird leztere
positiv seyn, und die Strahlen werden convergiren.
Beispiel. Die Brennweite einer doppelt convexen Linse
ist 6 Zoll, und einer concav-convexen Linse negativ 9 Zoll. Man verlangt
die Brennweite des aus diesen beiden zusammengesezten
Objectiv-Glases.
Von der negativen Brennweite
=
9 9
Ziehe man die positive ab
=
6 6
–– ––
3 54
3) 54
–––––
18 die
verlangte Brennweite.
Aus diesen Regeln lassen sich mehrere andere ableiten, die haͤufig
angewendet werden: z.B.
6) Wenn der Index der Refraction und einer der Halbmesser
einer doppelt convexen Linse gegeben ist, den anderen Halbmesser so zu
bestimmen, daß eine gegebene Brennweite zum Vorscheine kommt.
Regel. Man multiplicire die gegebene Brennweite, ein
Zehntel des Index a und den gegebenen Halbmesser zu
einem Dividenden, und subtrahire den ersten Theil dieses Productes von dem
gegebenen Halbmesser, und mache den Rest zum Divisor, theile den Dividenden
durch den Divisor, und der Quotient ist der andere Halbmesser.
Beispiel. Der Index eines Stuͤkes Flintglas
ist 1,600, und eine der Kruͤmmungen desselben hat einen Halbmesser von 10
Zoll: welcher andere Halbmesser gibt eine Brennweite von 12 Zoll?
a
=
0,600.
Brennweite
=
12
–––
7,2 = erstes Product
vonsubtrahire
10 7,2
Gegebener Halbm.
10
–––––
–––––
Divisor
2,8
72 Dividend
–––––
7) Aus dem gegebenen Index eines Stuͤkes Glas die
gleichen convexen Oberflaͤchen zur Bildung einer Brennweite von gegebener
Laͤnge zu finden.
Regel. Man multiplicire die Brennweite mit zwei
Zehntel Index: das Product ist der Halbmesser der beiden gleichen convexen
Oberflaͤchen.
Beispiel. Welche gleiche Halbmesser an einem
Stuͤke Glas
(wie oben 7) geben zwei gleich gekruͤmmte Oberflaͤchen zu einer
Brennweite von 6 Zoll.
Hier ist zwei mal a
= 1,2
Brennweite
= 6
–––––
7,2 Zoll der Halbmesser.
Bei einer plan-convexen Linse muß 1/10 Index mit der Lauge der Brennweite
multiplicirt werden.
8) Aus dem Brechungs-Index und aus der convexen
Oberflaͤche einer concav-convexen Linse den Halbmesser der
concaven Oberflaͤche zu finden, so daß diese Linse eine gegebene negative
Brennweite erhaͤlt.
Regel. Man finde den Dividenden genau, wie in Regel
6. Dann addire man das erste Product zu dem gegebenen Halbmesser, und bilde
hieraus den Divisor. Der Quotient ist der gesuchte Halbmesser.
Beispiel. Der Halbmesser der convexen
Oberflaͤche einer concav-convexen Linse ist 12 Zoll; der
Brechungs-Index 1,600; die negative Brennweite 5 Zoll: man will den
Halbmesser der concaven Oberflaͤche wissen.
Textabbildung Bd. 23, S. 17
Brennweite; Erstes Product;
Gegebener Halbmesser; Dividend; Divisor
9) Aus dem gegebenen Brechungs-Index und dem
Halbmesser der concaven Oberflaͤche den Halbmesser der convexen
Oberflaͤche zu finden, so daß die Linse eine gegebene negative Brennweite
erhaͤlt.
Regel. Man finde den Dividenden genau, wie in Regel
6. Man subtrahire den gegebenen Halbmesser von dem ersten Producte, und bilde
daraus den Divisor: der Quotient ist der verlangte Halbmesser.
Beispiel. Die Zahlen stehen wie in dem lezten
Beispiele, außer daß der Halbmesser der concaven Flaͤche 2,4 Zoll ist.
Man finde den anderen Halbmesser.
Erstes Product
= 3,0
Gegebener Halbmesser
= 2,4
–––––––
3,0 – 2,4 =
0,6) 72
–––––––
Gesuchter Halbmesser
=
12
Zoll.
Anmerkung.
Auf aͤhnliche Weise kann aus den Halbmessern der Kruͤmmung einer
Linse, und der durch Versuch gefundenen Brennweite, der Index der Brechung
derselben sehr genau berechnet werden. Ueber diesen Gegenstand finden sich
einige Bemerkungen am Ende dieser Abhandlung.
Wir koͤnnen nun zur Berechnung der Halbmesser eines zusammengesezten
achromatischen Objectiv-Glases uͤbergehen, wenn der
Brechungs-Index und die Zerstreuungskraͤfte der Glaͤser
gegeben ist.Edinb. phil. Journ. N. 28. S. 311.
15. Detail zur Berechnung eines
zusammengesezten achromatischen Objectiv-Glases.
Es ist am besten in diesem Falle die Rechnung immer fuͤr eine gegebene
Brennweite zu fuͤhren, und hierauf die Kruͤmmungen in geradem
Verhaͤltnisse der vorgeschlagenen Brennweite zur angenommenen zu
veraͤndern. Unsere angenommene zusammengesezte Brennweite ist immer 10
Zoll.
Das Beispiel, welches wir hier vortragen, ist die Berechnung der Kruͤmmungen
eines zusammengesezten Objectiv-Glases aus zwei Stuͤken Tafel-
und Flint-Glas, mit welchen in der Einleitung Versuche angestellt werden. Der
Brechungs-Index des Tafel-Glases ist 1,528, des Flint-Glases
1,601; das Zerstreu-Verhaͤltniß beider 0,683: folglich die
erforderliche Brennweite 46 Zoll.
Die gehoͤrige Brennweite der beiden das
Objectiv-Glas bildenden Linsen zu finden, so daß sie im
Verhaͤltnisse der Zerstreunngs-Kraͤfte gegen einander
stehen, und eine zusammengesezte Brennweite von 10 Zoll haben.
Regel 1) Man subtrahire die Zahl, die das
Zerstreuungs-Verhaͤltniß ausdruͤkt, von der Einheit, und der
Rest multiplicirt mit 10 ist die Brennweite der Tafelglas-Linse.
2) Man theile die auf obige Weise gefundene Brennweite der Tafelglas-Linse
durch das Zerstreuungs-Verhaͤltniß; der Quotient wird die Brennweite
der Flint-Linse seyn.
Beispiel. Fuͤr den angegebenen Fall war das Zerstreuungs-Verhaͤltniß 0,683;
folglich
von
1,000
abgezogen
0,683
–––––
Rest
0,317
Multiplicirt
mit 10
–––––
3,17 Zoll Brennweite der
Tafelglas-Linse.
0,683)
3,170 (4,64 Zoll Brennweite der
Flintglas-Linse.
Die erste oder aͤußere Oberflaͤche der
Tafelglas-Linse, und die vierte oder vordere Flaͤche der
Flintglas-Linse fuͤr eine zusammengesezte Brennweite von 10 Zoll
zu finden.
Hier muͤssen wir zu den am Ende beigefuͤgten Tafeln unsere Zuflucht
nehmen, und auf folgende Weise verfahren. In der ersten Spalte dieser Tafeln, welche
alle Zerstreuungs-Verhaͤltnisse, die jemahls in der Praxis vorkommen
koͤnnen, enthaͤlt, sucht man das in Frage stehende, z.B. in unserem
Falle, 0,683, und in derselben Linie wird man in der zweiten und fuͤnften
Spalte die gehoͤrigen Halbmesser der Kruͤmmung fuͤr die erste
und vierte Oberflaͤche finden, unter der Voraussezung, daß der
Brechungs-Index des Tafel-Glases 1,524, und des Flint-Glases
1,585 ist; denn fuͤr diese Zahlen ist diese Tafel berechnet. In unserem Falle
sind diese Zahlen 6,7956 und 12,7423. Wenn aber die Index nicht, wie in diesem
Falle, so, wie an dem vorliegenden Glase, sind, muͤssen die obigen Halbmesser
in der Tabelle auf folgende Weise corrigirt werden.
Fuͤr die Linse aus Tafel-Glas. Man finde
die Differenz zwischen dem Index der Tabelle fuͤr das Tafelglas, und jenem
des in Frage stehenden Glases, und multiplicire mit dieser Differenz die in der
dritten Spalte stehende Zahl. Wenn der gegebene Index großer ist, als jener in der
Tafel, so seze man das Zeichen (plus oder minus) wie man es in der Tafel findet, vor das
Product; wenn aber der Index in der Tafel großer ist, dann seze man das
entgegengesezte Zeichen von demjenigen, welches' sich in der Tafel findet, vor das
Product.
Hierauf nimmt man die Differenz zwischen dem gegebenen Index des Flintglases und
jenem in der Tafel, und verfaͤhrt genau auf dieselbe Weise, naͤmlich,
man multiplicirt diese Differenz mit der Zahl in der vierten Spalte, und befolgt,
in. Hinsicht auf das Zeichen vor dem Producte, die oben gegebene Regel.
Nun addirt man, wenn die beiden Producte dasselbe Zeichen haben, dieselben zu einander;
wenn sie aber verschiedene Zeichen haben, so subtrahirt man sie, und sezt das
gehoͤrige Zeichen vor: d.h., das Zeichen der Producte selbst, wenn sie gleich
sind, oder das des groͤßeren, wenn sie verschieden sind.
Endlich, wenn das resultirende Zeichen plus (+)
ist, so addire man die Zahl, vor welcher es steht, zu dem oben gefundenen Halbmesser
der Tabelle; wenn es minus (–) ist, so
ziehe man sie ab: die Summe oder der Rest gibt den verbesserten Halbmesser
fuͤr die erste Oberflaͤche des Tafel-Glases.
Auf dieselbe Weise verfaͤhrt man mit der Flintglas-Linse, und bedient
sich der 5. 6. und 7. Spalte, und erhaͤlt auf diese Weise den verbesserten
Halbmesser fuͤr die vierte Oberflaͤche.
Diese Regeln sind in folgender Fortsezung des Beispieles
erlaͤutert.
Da das Zerstreuungs-Verhaͤltniß unseres Flint- und
Tafel-Glases, nach Versuchen, 0,683 ist, so werden die Halbmesser nach dem
Brechungs-Index der Tafel fuͤr die erste Oberflaͤche = 6,7956
Zoll, und fuͤr die vierte Oberflaͤche 12,7423 Zoll.
Diese muͤssen nun fuͤr den gegebenen Index, naͤmlich fuͤr
Tafel-Glas =1,528, und fuͤr Flint-Glas = 1,601, verbessert
werden.
Die Differenz zwischen dem Index der Tafel fuͤr das Tafel-Glas, und dem
gegebenen ist 0,004. Daher
Zahl in der dritten Spalte =
+
0,414
Multiplicirt mit
0,004
––––––
Gibt
+
0,01656
Die Differenz zwischen dem Index der Tafel fuͤr das Flint-Glas und dem
gegebenen ist 0,016. Daher
Zahl in der vierten Spalte
=
+ 2,45
Multiplicirt mit
0,016
–––––––
Gibt
+
0,03920 verbesserten Tafel-Glas Index.
Addire
+
0,01656 verbesserten Flint-Glas Index.
–––––––
Summe
+
0,05576 verb.
Addire Halbmesser der Tafel
6,7956
–––––––
Verbesserter Halbmesser
6,8514 fuͤr die erste Oberflaͤche.
Ferner, Zahl in der sechsten Spalte
=
+ 116,14
Multiplicirt mit
0,004
–––––––
Gibt
+ 0,46456 verb. Tafel-Glas
Index.
–––––––
Und, Zahl in der siebenten Spalte
=
–
71,69
Multiplicirt mit
0,016
––––––––
Gibt
–
1,14704
verbesserter Flint-Glas Index.
+
0,46456
––––––––
Differenz
–
0,68248
verbessert
Halbmesser der Tafel
12,7422
––––––––
12,0597
verbesserter Halbmesser fuͤr die vierte
Oberflaͤche.
Es bleibt nun nur noch die zweite und dritte Oberflaͤche, (d.h. die sich
beruͤhrenden Oberflaͤchen) zu bestimmen uͤbrig. Zu dieser
Bestimmung haben wir fuͤr jede Linse die Brennweite, den Halbmesser der einen
Oberflaͤche, und den Brechungs-Index gegeben; also fuͤr die
doppelt convexe, oder Tafelglas-Linse hier Regel 6, Art. 14, und fuͤr
die Flintglas-Linse, die concav-convex ist, Regel 8. desselben
Artikels.
Fuͤr die zweite Oberflaͤche der Tafelglas-Linse siehe Reg.
6.
Brennweite = 3,17. Ein Zehntel Index = 0,528;
3,17 × 0,528 = 1,67376 Erstes Product.
Halbmesser der ersten Oberflaͤche = 6,85
Erstes Product × Halbmesser d. ersten Oberflaͤche =
11,4627 = Dividend.
6,85 – 1,67376 = 5,17 = Divisor.
5,17) 11,4627 (2,22 = zweite Oberflaͤche.
Fuͤr die dritte Oberflaͤche der concaven Flint-Linse, siehe
Regel 8, Artikel 14.
Brennweite = 4,64. Ein Zehntel Index = 0,601;
4,64 × 0,601 = 2,788 = Erstes Product.
12,06 = gegebener Halbmesser
2,788 × 12,06 = 33,62328 = Dividend.
12,06 + 2,788 = 14,848 = Divisor.
14,848) 33,62328 (2,26 = Halbmesser der dritten
Oberflaͤche.
Wir haben so die vier folgenden Halbmesser fuͤr die auf einander folgenden
Oberflaͤchen zu einer zusammengesezten Brennweite von 10 Zoll,
naͤmlich:
Tafel-Glas
1ste Oberflaͤche Halbmesser 6,85
Zoll convex,2ste Oberflaͤche Halbmesser 2,22
Zoll convex,
Flint-Glas
3ste Oberflaͤche Halbmesser 2,26
Zoll concav.4ste Oberflaͤche Halbmesser 12,060 Zoll
convex.
Diese sind, wie man bemerken wird, fuͤr eine zusammengesezte Brennweite von 10
Zoll, waͤhrend unser Beispiel eine von 46 Zoll fordert. Wir muͤssen
daher diese verschiedenen Halbmesser in dem Verhaͤltnisse von 10 zu 46 vergroͤßern, was
folgende Resultate gibt:
10 : 46 : : 6,85 :
31,510 erste
Oberflaͤche
convex,
10 : 46 : : 2,22 :
10,212 zweite
–
convex,
10 : 46 : : 2,26 :
10,396 dritte
–
concav,
10 : 46 : : 12,060 : 55,476 vierte
–
convex.
Wenn der Umstand, daß die zweite beruͤhrende Oberflaͤche, d.i., die
convexe, die tiefere von beiden ist, in praktischer Hinsicht unbequem ist, oder wenn
man es gut faͤnde, daß diese Oberflaͤchen auf gleichen Werkzeugen
gearbeitet wuͤrden, so wird es sehr leicht seyn, die dritte
Oberflaͤche zu reduciren, so daß sie der zweiten gleich wird, wenn man eine
solche correspondirende Veraͤnderung an der vierten Oberflaͤche
anbringt, daß immer dieselbe Brennweite erhalten wird, sowohl einzeln fuͤr
die Flint-Linse, als fuͤr die zusammengesezte Brennweite. Wir haben
bloß 2,22 Zoll als den gegebenen Halbmesser, 4,64 als die Brennweite unter einem
Index von 1,601 zu betrachten, und die vierte correspondirende Oberflaͤche
nach der hierzu gegebenen Regel 9, Art. 14, zu finden.
Brennweite = 4,64. Ein Zehntel Index = 0,601;
4,64 × 0,601 = 2,78864 = Erstes Product.
2,22 = gegebener Halbmesser.
2,78864 × 2,22 = 6,19047 = Dividend.
2,788 – 2,22 = 0,568 = Divisor.
0,568) 6,19047 (10,396 = Halbmesser der vierten
Oberflaͤche.
Und dann:
10 : 46 : : 10,898 : 50,13 Zoll.
Diese Einrichtung gibt demnach fuͤr die vier
Oberflaͤchen,
1ste2te3te4te
Oberflaͤche – – –
====
31,51010,21210,21250,13
zusammengesezte Brennweite 46 Zoll.
Man muß jedoch bemerken, daß diese Veraͤnderungen so wenige als
moͤglich gemacht werden muͤssen, weil sie leicht Mangel an Genauigkeit
oder Mangel an Compensation veranlassen, obschon sie in gewoͤhnlichen
Faͤllen ohne einen sehr bedeutenden Fehler angewendet werden koͤnnen.
Es ist offenbar, daß wir haͤtten ein Mittel zwischen den beiden sich
beruͤhrenden Halbmessern nehmen, und darnach die erste und vierte
Oberflaͤche vorrichten koͤnnen.
Es gibt noch einen anderen praktischen Kunstgriff, zu welchem man zuweilen seine
Zuflucht nehmen kann, und der, inner halb gewisser Graͤnzen, keinen Fehler veranlaßt;
dieser ist naͤmlich der, wenn der Arbeiter ein Paar Contact-Werkzeuge
hat, die beinahe so sind, wie die Rechnung sie fordert. In diesem Falle kann er,
statt seine Werkzeuge zu aͤndern, alle Halbmesser in dem Verhaͤltnisse
abaͤndern, in welchem die verlangten Halbmesser zu den erwaͤhnten
Werkzeugen stehen. Dieß gibt Ein bis zwei Zoll Differenz in der Brennweite des
Objectiv-Glases, was von keiner besonderen Bedeutung ist.
Man seze z. B. der Arbeiter haͤtte, fuͤr den lezten Fall, ein Paar
Contact-Werkzeuge, die genau 10 Zoll messen; so braucht er bloß zu sagen:
10,212 : 10 : : 31,51 : 30,85 = 1ste Oberflaͤche.
10,212 : 10 : : 50,13 : 49,09 = 4te Oberflaͤche.
10,212 : 10 : : 46,00 : 45,09 = Brennweite.
Auf diese Weise erhalten wir folgende Resultate:
1ste2te3te4te
Oberflaͤche – – –
30,8510,0010,0049,09
Brennweite 45,09 Zoll.
So geht die Rechnung zur Bestimmung der Halbmesser der Kruͤmmung bei
Verfertigung eines achromatischen Objectiv-Glases, von welcher wir hier noch
ein zweites Beispiel geben wollen.
2tes Beispiel.
Man soll die Halbmesser der Kruͤmmung fuͤr ein Objectiv-Glas von
6 Fuß Brennweite aus Newcastle Tafel-Glas, dessen Index 1,515, und aus
Schweizer Flint-Glas, dessen Index 1,671, unter
Zerstreuungs-Verhaͤltniß von 0,613 ist, bestimmen.
1,000
0,613
–––––
0,387
10
–––––
3,87 = Brennweite der Tafelglas-Linse.
0. 613) 3,870
(6,31 = Brennweite der Flintglas-Linse.
Halbmesser nach der Tafel unter0,613
Zerstreuungs-Verhaͤltniß
1ste Oberflaͤche
= 6,71314ste Oberflaͤche = 14,1052
Index der Tafel fuͤr Tafelglas
1,524
fuͤr Flintglas
1,585
Gegebener Index fuͤr dasselbe
1,515
– dasselbe
1,671
–––––
––––––
– 0,009
+
0,086
Verbesserung der ersten Oberflaͤche
Verbesserter Index d. Tafel f. Tafelglas
=
+ 6,46
fuͤr Flintglas
=
+ 0,600
– 0,009
+ 0,086
––––––––
–––––––
–
0,05814
+ 0,0516
+
0,05160
––––––––
–
0,00654
= Verbesserung
6,7131
––––––––
Erste Oberflaͤche
6,70666
= verbesserter Halbmesser.
Verbesserung der vierten Oberflaͤche.
N. d. Tafel verbess. Tafelglas-Ind. =
+
111,90
Flintglas Index =
–
58,32
–
0,009
+
0,086
––––––––
–––––––
–
1,00764
0,34992
–
5,01552
4,6656
––––––––
–
6,02316
= Verbesserung.
–
5,01552
14,1052
––––––––
vierte Oberflaͤche
8,08204
= verbesserter Halbmesser
Die beruͤhrenden Oberflaͤchen zu
finden.
Brennweite der Tafelglas-Linse = 3,87. Ein Zehntel des
Index des Tafelglases = 0,515.
3,87 × 0,515 = 1,993 = Erstes Product.
Halbmesser der ersten Oberflaͤche = 6,706.
1,993 × 6,706 = 13,365058 = Dividend.
6,706 – 1,993 = 4,713 = Divisor.
4,713) 13,365058 (2,836 = Halbmesser der zweiten
Oberflaͤche.
Brennweite der Flintglas-Linse = 6,31. Ein Zehntel des
Index des Flintglases = 0,671.
6,31 × 0,671 = 4,234 = Erstes Product,
8,082 = Halbmesser der vierten
Oberflaͤche.
4,234 × 8,082 = 34,219188 = Dividend,
8,082 + 4,234 = 12,316 =
Divisor.
12,316) 34,219188(2,778 = Halbmesser der dritten
Oberflaͤche.
Daher fuͤr eine zusammengesezte Brennweite von 10 Zoll
folgende Resultate.
Tafel-Glas
1ste Oberflaͤche
Halbmesser2te – –
6,706 convex,2,836 convex,
Flint-Glas
3te – –4te – –
2,778 concav,8,082 convex.
Daher endlich fuͤr unsere zusammengesezte Brennweite von 72 Zoll:
10 : 72 : : 6,706 : 48,28 = 1ste10 :
72 : : 2,836 : 20,42 = 2te10 : 72 : :
2,778 : 20,00 = 3te10 : 72 : : 8,082 : 58,19 =
4te
Oberflaͤche – – –
Brennweite 72 Zoll.
Obige Beispiele werden vollkommen hinreichen, um jeden praktischen Optiker in den
Stand zu sezen, die oben gegebenen Operationen, nicht bloß insofern sie zu
Berechnung der Halbmesser dienen, sondern auch zur Bestimmung des
Brechungs-Index und des Zerstreuungs-Verhaͤltnisses der
Glaͤser zu verfolgen. Sie sind fuͤr diejenigen berechnet, denen
algebraische Formeln nicht gelaͤufig sind, und wir entschuldigen uns daher
nicht vor den Algebraisten wegen der Laͤnge, die einige Berechnungen und
Erlaͤuterungen hier einnehmen; sie koͤnnen sie ja nach Belieben
abkuͤrzen. Wir muͤssen hier noch bemerken, daß man bei der weiteren
Ausdehnung, die der unten folgenden Tabelle gegeben wurde, keinen anderen Grundsaz
befolgte, als bloß jenen des einfachen Verhaͤltnisses: sie ist
hinlaͤnglich genau fuͤr jeden praktischen Zwek.
Tafel der Halbmesser der ersten und vierten Oberflaͤche
der Objektiv-Glaͤser fuͤr verschiedene
Zerstreuungs-Verhaͤltnisse und fuͤr den
Berechnungs-Index von 1,524 fuͤr Tafel- und 1,585 fuͤr
Flint-Glas, nebst Spalten fuͤr Verbesserungen bei einem anderen
Index.
Textabbildung Bd. 23, S. 25
Erste Oberflaͤche; Vierte
Oberflaͤche; Zerstreuungs-Verhaͤltniß Halbmesser
fuͤr den Index; Verbesserung des Index fuͤr Tafel-Glas;
Verbesserung des Index fuͤr Flint-Glas
Fortsezung der Tafel.
Textabbildung Bd. 23, S. 26
Erste Oberflaͤche; Vierte
Oberflaͤche; Zerstreuungs-Verhaͤltniß; Halbmesser
fuͤr den Index; Verbesserung des Index fuͤr Tafel-Glas;
Verbesserung des Index fuͤr Flint-Glas
Fortsezung der Tafel.
Textabbildung Bd. 23, S. 27
Erste Oberflaͤche; Vierte
Oberflaͤche; Zerstreuungs-Verhaͤltniß Halbmesser
fuͤr den Index; Verbesserung des Index fuͤr Tafel-Glas;
Verbesserung des Index fuͤr Flint-Glas
Fortsezung der Tafel.
Textabbildung Bd. 23, S. 28
Erste Oberflaͤche; Vierte
Oberflaͤche; Zerstreuungs-Verhaͤltniß Halbmesser
fuͤr den Index; Verbesserung des Index fuͤr Tafel-Glas;
Verbesserung des Index fuͤr Flint-Glas
Tafeln