| Titel: | Untersuchungen über das Leitungs-Vermögen dünner Körper, welche der Einwirkung der Wärme ausgesezt sind, und Beschreibung eines neuen Berührungs-Thermometers. Von Herrn Fourier. |
| Fundstelle: | Band 29, Jahrgang 1828, Nr. XLIV., S. 161 |
| Download: | XML |
XLIV.
Untersuchungen uͤber das
Leitungs-Vermoͤgen duͤnner Koͤrper, welche der Einwirkung
der Waͤrme ausgesezt sind, und Beschreibung eines neuen
Beruͤhrungs-Thermometers. Von Herrn Fourier.
Aus den Annales de Chimie et de Physique. Maͤrz
1828. S. 291.
Mit Abbildungen auf Tab.
IV.
Fourier's Untersuchungen uͤber das
Leitungs-Vermoͤgen duͤnner Koͤrper.
Die Abhandlung, welche ich der Akademie vorlege, hat zum Zwek,
die Resultate einiger neuerdings mit einem Beruͤhrungs-Thermometer
angestellten Versuche bekannt zu machen. Dieses Instrument zeigt die groͤßere
oder geringere Leichtigkeit an, womit die Waͤrme Blaͤttchen oder
duͤnne Blaͤtter verschiedener Koͤrper durchdringt; es dient so,
um die Huͤlsen, welche sich dem freien Durchlassen der Waͤrme
widersezen, nach Verhaͤltniß ihrer Leitungskraft aneinander zu reihen.
Wenn Koͤrper von verschiedener Natur sehr lange Zeit an einem und demselben
Orte verbleiben, und wenn die Temperatur des Umfanges, welcher diesen Raum
begraͤnzt, einen bestaͤndigen Werth erlangt hat und auch
behaͤlt, so werden alle diese Koͤrper die bestaͤndige und
eigenthuͤmliche Temperatur des Umfanges annehmen. Ein Thermometer, welches
auf die verschiedenartigsten Oberflaͤchen, zum Beispiel auf
Metallblaͤttchen, Gewebe aus Wolle, Baumwolle, Flachs, auf Filz oder andere
Substanzen gesezt wird, wird immer denselben Grad zeigen; beruͤhrt man aber
diese Substanzen, so wird die Hand sehr verschiedene Temperaturen fuͤhlen;
gewisse Oberflaͤchen, wie die der Metalle oder des Marmors, werden bei der
Beruͤhrung viel kaͤlter als andere scheinen, obgleich sie alle gleiche
Temperatur haben.
Der physikalische Grund dieser Thatsache ist allgemein bekannt. Es ist offenbar, daß
die Hand des Beobachters, weil sie waͤrmer als die beruͤhrten
Oberflaͤchen ist, schnell einen Theil ihrer eigenen Oberflaͤche fahren
laͤßt, welcher sich den umgebenden Massen mittheilt. Nun besizen aber die
verschiedenen Koͤrper das Vermoͤgen, die Waͤrme, welche sie
enthielten, aufzunehmen und fahren zu lassen, sehr ungleich; gerade dieses
Leitungsvermoͤgen nahm ich mir vor, zu beobachten und zu messen. Der Gebrauch
unserer Sinne ist allein schon hinreichend, um diese eigenthuͤmlichen
Eigenschaften zu unterscheiden; die Kunst kann sie aber noch viel merklicher machen,
und sie gibt uns, was wichtig ist, ihr genaues Maß.
Einige Physiker und besonders Herr Leslie aus Edinburgh
und der Graf Rumford hatten, indem sie die Dauer des
Erkaltens der Fluͤssigkeiten in Gefaͤßen, welche mit verschiedenen
Umschlaͤgen bekleidet waren, beobachteten, uns gezeigt, welchen Einfluß der
Zustand der Oberflaͤche auf die Ausstrahlung und den Verlust der
Waͤrme haben. Die mathematische Theorie bietet verschiedene andere Mittel
dar, die Durchdringbarkeit der Koͤrper zu messen. Es ist hinreichend, wie ich
gezeigt habe, die veraͤnderliche Bewegung der Fluͤssigkeiten in
Gefaͤßen, welche sich in Materie und Dike unterscheiden, sehr genau zu
beobachten, oder den unwandelbaren Zustand, welcher nach einer gewissen Zeit
eintritt, zu bestimmen. Die Beobachtungen dieser Art werden mit der Zeit
schaͤzbare Tabellen liefern, welche die Eigenschaften aller Koͤrper in
Hinsicht auf die Waͤrme anzeigen. Der Gebrauch des neuen
Beruͤhrungs-Thermometers hat keinen so ausgedehnten Zwek. Er muß
diesen theoretischen Untersuchungen vorangehen und sie erleichtern, indem er eine
ziemlich genaue Kenntniß einer sehr großen Anzahl von Resultaten verschafft. Dieses
Instrument kann in zwei verschiedenen Formen verfertigt werden. Ich habe mit beiden
Versuche angestellt, und es schien mir nuͤzlich, einige dieser Beobachtungen
bekannt zu machen.
Ich ließ zuerst vor einigen Jahren das außerordentlich einfache Instrument, welches
ich jezt beschreiben will, verfertigen. Es besteht aus einem kegelfoͤrmigen
Gefaͤße von sehr duͤnnem Eisen, welches mit Queksilber gefuͤllt
und an seiner unteren kreisfoͤrmigen Basis mit einer mittelmaͤßig
diken Haut bekleidet ist. Ein Thermometer, dessen Kugel in das Queksilber getaucht
wird, zeigt jeden Augenblik die Temperatur der fluͤssigen Masse an; die Figur (1) zeigt
die verschiedenen Theile des Instrumentes; A, A, ist das
kegelfoͤrmige mit Queksilber gefuͤllte Gefaͤß; b, b, b, die biegsame Oberflaͤche, welche die
Fluͤssigkeit enthaͤlt; C, C, das innere
Thermometer, welches in das Queksilber taucht; D, die
Stuͤze, welche auf einer bestimmten Temperatur, z.B. derjenigen der Kammer,
worin man arbeitet, erhalten wird. Zuerst erhizt man nun und zwar einzig und allein
das kegelfoͤrmige Gefaͤß, A, bis auf eine
bestimmte Temperatur, die von 40 Graden (Centeskl.); alsdann, wenn man auf die
Stuͤze die duͤnne Platte oder das Blaͤttchen, dessen
Leitungskraft man messen will, gebracht hat, sezt man auf dieses Blaͤttchen
das kegelfoͤrmige Gefaͤß mit Queksilber; hierauf beobachtet man
sorgfaͤltig die fortschreitende Erkaltung, indem man die verflossenen Zeiten
und die entsprechenden Temperaturen bemerkt.
Das Gesez der Erkaltung wird durch eine Differenzial-Gleichung
ausgedruͤkt; der vollstaͤndige Ausdruk dieses Gesezes enthaͤlt
die fixe Temperatur der
Stuͤze, die der umgebenden Luft und einen Exponent, welcher von dem
Leitungsvermoͤgen der Substanzen abhaͤngt, die die Waͤrme
durchdringt. Man kann also das Maß dieses Vermoͤgens aus demjenigen der
fuͤr verschiedene Zeitwerthe beobachteten Temperaturen ableiten. Auf folgende
Art erhaͤlt man den Ausdruk fuͤr die Bewegung der Waͤrme. Wir
bezeichnen durch die Waͤrmemenge, welche waͤhrend der Zeiteinheit von
der Oberflaͤche des kegelfoͤrmigen Gefaͤßes in die Luft
ausstroͤmen wuͤrde, wenn die Groͤße dieser Oberflaͤche =
1 angenommen, die Differenz zwischen der Temperatur der Luft und der fixen
Temperatur der Oberflaͤche gleich 1 waͤre. Wenn nun α die wirkliche Temperatur des erhizten
kegelfoͤrmigen Gefaͤßes, S, die
Groͤße seiner Oberflaͤche und dt das
Element der verflossenen Zeit ist, erhaͤlt man
Textabbildung Bd. 29, S. 163
fuͤr die Quantitaͤt der Waͤrme, welche
waͤhrend des Augenbliks dt, von der
Oberflaͤche des Gefaͤßes in die Luft ausstroͤmt, wovon m die fixe Temperatur bezeichnet. Man mißt die
Waͤrmemengen, indem man bezeichnet, wie oftmahls sie eine gewisse als Einheit
angenommene Quantitaͤt enthalten; H bezeichnet
eine gewisse Anzahl dieser Einheiten.
Man bezeichnet durch h die Waͤrmemenge, welche
waͤhrend der Zeiteinheit die Einheit der Oberflaͤche durchdringen und
aus der erhizten kegelfoͤrmigen Masse A in die
Stuͤze D ausstroͤmen wuͤrde, wenn
die Differenz zwischen der Temperatur von A, und
derjenigen von der Stuͤze 1 (100 Centesimalgrade) waͤre. So ist,
Textabbildung Bd. 29, S. 163
die Waͤrmemenge, welche aus dem Gefaͤß in die
Stuͤze ausstroͤmt, deren fixe Temperatur durch n vorgestellt wird, wenn b die Groͤße
derjenigen Oberflaͤche ist, welche die Stuͤze beruͤhrt; es
druͤkt also
Textabbildung Bd. 29, S. 163
die Waͤrme aus, welche das Gefaͤß
waͤhrend des Augenblikes dt verliert. Wenn
man nun durch c die Waͤrme bezeichnet, welche,
wenn sie zu derjenigen, die die Masse A enthaͤlt,
hinzukommt, von der wir voraussezen, daß sie auf der Temperatur 0 ist, diese Masse
von der Temperatur 0 auf die Temperatur 1 bringen wuͤrde, so wird man die
Differizialgleichung
Textabbildung Bd. 29, S. 163
als Ausdruk der veraͤnderlichen Bewegung der
Waͤrme erhalten. Man integrirt diese Gleichung leicht, wenn man schreibt
Textabbildung Bd. 29, S. 163
denn wenn man diesen Werth dem α in der Gleichung (1) substituirt, so verificirt man die Gleichung
und hat nur die Bedingung
Textabbildung Bd. 29, S. 163
Nun wollen wir durch αo, αθ, α2θ drei auf einander
folgende Temperaturen bezeichnen, welche man naͤmlich am Ende dreier
Zeitzwischenraͤume, wovon jeder gleich θ
ist, beobachtet und durch ρ den
Exponenten-Coëfficient
(hb + Hs)/c
bezeichnen, welchen man als unbekannt betrachtet, und man wird
daraus den Werth von ρ, welcher aus den drei
beobachteten Temperaturen abgeleitet ist, folgern koͤnnen, denn man hat:
αo = P + Q
αθ = P + Qe– ρθ
α2θ = P + Qe–
2ρθ
also αo – αθ = Q (1
– e–
ρθ)
αθ – α2θ = Qe– ρθ (1 – e–
ρθ)
und
Textabbildung Bd. 29, S. 164
also ρ = 1/θ {log (αo – αθ)
– log. (αθ – α2θ)}
Daraus folgt, daß man den Werth von ρ oder
hb/c + Hs/c
durch folgende Regel erfahren wird: man muß die drei
Temperaturen αo
αθ
α2θ
beobachten, die hyperbolischen Logarithmen von αo – αθ
und αθ – α2θ nehmen und die Differenz dieser
Logarithmen durch die Zwischenzeit θ
dividiren.
Wenn man den Versuch mit einer gewissen dazwischen gelegten Substanz, welcher der
Coëfficient h zukommt, gemacht hat und mit
demselben Instrument mit einer anderen Substanz, welcher ein anderer
Coëfficient h' entspricht, den Versuch
wiederholt, und das Resultat mit dem ersteren vergleichen will, so bestimmt man
durch die so eben angefuͤhrte Regel, indem man bloß die Logarithmen der
Tabellen anwendet, die den unbekannten Coëfficienten
hb/c + Hs/c
entsprechenden Groͤßen.
Die Groͤßen Hsbe sind gemeinschaftlich, und
die beiden Resultate werden sich nur durch die Coëfficienten h und h' unterscheiden.
Pruͤft man also nach einander mehrere verschiedene Substanzen, welche man in
Hinsicht ihrer Leitungsfaͤhigkeit vergleichen will, und berechnet mittelst
der vorhergehenden Regel die respectiven Zahlen, welche man durch die mit demselben
Instrument gemachten Beobachtungen erhaͤlt, so wird man nicht die absoluten
Werthe der Coëfficienten h h'h''h''', u.s.w.,
sondern eine Zahlenfolge kennen, deren Zunahme der Zunahme der Werthe h h'h''h''', u.s.w. proportional ist. So koͤnnen
durch dieses Verfahren die verschiedenen Substanzen nach ihrer
eigenthuͤmlichen Leitungsfaͤhigkeit aneinander gereiht werden, was
diese Untersuchung bezwekt, und wenn die Leitungsfaͤhigkeiten der Substanzen,
welche man vergleicht, in gleichem Grade zunehmen, so werden die durch die
Beobachtung gegebenen Zahlen auch in gleichem Grade wachsen. Man braucht also nur
aus einer sehr großen Anzahl von Beobachtungen die gleich weit abstehenden Resultate
zu waͤhlen, um versichert zu seyn, daß die Leitungsfaͤhigkeiten der
Substanzen, welchen diese Zahlen entsprechen, auch nach demselben Geseze wachsen. Es
ist zu bemerken, daß der Coëfficient h nicht die
Waͤrmemenge ausdruͤkt, welche das duͤnne Blatt oder die
dazwischengelegte Huͤlse durchstreicht; er begreift auch die
Waͤrmemenge in sich, welche die biegsame Oberflaͤche durchdringt, die
unter dem Queksilber des kegelfoͤrmigen Gefaͤßes angebracht ist. Wenn
nun aber eine solche Groͤße zu allen Werthen, welche man vergleichen will,
hinzu addirt wird, so aͤndert sie an den Folgerungen, welche man daraus
herleitet, nichts. So wird die Zunahme der Zahlen, welche man durch die
logarithmische Regel erhalten hat, bestaͤndig der Zunahme der gesuchten
Coëfficienten proportional seyn.
Nun wollen wir den Fall betrachten, wo die Temperatur der Stuͤze der
Temperatur der Luft gleich waͤre, welcher die Verfahrungsweisen einfacher
machen und ihre Anwendung erleichtern wuͤrde. Wenn man bei dem vorhergehenden
Werthe von P, m = n macht, findet man P = m. Offenbar muß in diesem Falle die endliche
Temperatur des Gefaͤßes diejenige der Luft seyn. Wenn man also t in der Gleichung (2) als unendlich groß annimmt, so
findet man αoo = m. In der That wird dieses Statt finden,
wenn P = m. Die veraͤnderliche Temperatur α ist also m + Qe–ρt. Beobachtet man daher zwei auf
einander folgende Temperaturen, so wird man den Exponenten-Coëfficient
ρ bestimmen koͤnnen. Man wird haben
αo =
m + Q und α = m + Qe–ρθ und wenn, man fuͤr Q seinen Werth αθ – m, sezt:
Textabbildung Bd. 29, S. 166
also ρ = 1/θ
[log. (αθ – m) – log. (αo – m)].
Man braucht also nur αoαθ zu beobachten und durch den Zeitraum
θ die Differenz der Logarithmen der Tabellen
von αo– m und αθ–
m zu dividiren; der Quotient ist dem Werthe von ρ proportional, welcher ist
Hs/c + hb/c.
Uebrigens ist der Gebrauch des von mir beschriebenen
Beruͤhrungs-Thermometers unvermeidlichen Abweichungen unterworfen,
welche ohne Zweifel merkliche Differenzen zwischen der Theorie und der Beobachtung
herbeifuͤhren koͤnnten. Die Stuͤze behaͤlt keine ganz
bestaͤndige Temperatur bei; die in dem Gefaͤße enthaltene Masse,
welche sich erkaͤltet, ist nicht genau in dem Zustande, welchen die Theorie
voraussezt. Diese Ursachen, und andere, welche nicht erst angefuͤhrt zu
werden brauchen, muͤssen, wie ich glaube, in den Resultaten Differenzen
herbeifuͤhren, welche den aufmerksamsten Beobachtungen entgingen. In allen
Faͤllen aber wuͤrden die annaͤhernden Resultate, welche man
beim Gebrauche dieses Instrumentes erhaͤlt, hinreichen, um die verschiedenen
Umschlaͤge oder duͤnnen Blaͤttchen, welche man vergleichen
will, nach ihrer Leitungsfaͤhigkeit an einander zu reihen, was der Hauptzwek
dieser Untersuchungen ist. Man hat besonders die Leichtigkeit und Mannigfaltigkeit
der Beobachtungen zu beruͤksichtigen. Man wird fuͤr die erste
Temperatur αo– m einen gemeinschaftlichen Werth, 40
Centesimalgrade; und fuͤr θ eine bestimmte
Dauer, zehn Minuten waͤhlen; man wird die Temperatur αθ – m beobachten, welche das Thermometer nach
Verlauf von 10 Minuten anzeigt. Diese Werthe von αθ – m, welche nach der Temperatur der Substanzen,
welche die Waͤrme durchdringt, verschieden ausfallen werden, werden geradezu
und ohne Berechnung die Reihe der specifischen Leitungsfaͤhigkeiten
angeben.
Offenbar hat die Dike der dazwischen gelegten Platte auf die Temperaturen, welche man
beobachtet, Einfluß, und man koͤnnte diese Dike in Rechnung bringen, wenn man
die Grundsaͤze, welche ich in meiner Introduction
à la Théorie de la chaleur aus einander gesezt habe, befolgen
wuͤrde; man betrachtet aber hier nur die vollstaͤndige und
zusammengesezte Wirkung, naͤmlich die Waͤrmemenge, welche, wenn sie die dazwischen
liegenden Oberflaͤchen durchdringt, von dem Queksilber in die Stuͤze
geht.
Wenn man das Blatt oder die Huͤlse, welche man zuerst gepruͤft hat,
durch einen duͤnnen Koͤrper aus einer anderen Materie ersezt, und
neuerdings die einer gegebenen Zeit entsprechende Temperatur-Erniedrigung
mißt, so findet man, daß leztere auf eine sehr merkliche Art wechselt, wie klein
auch der Unterschied zwischen den beiden Huͤlsen seyn mag. Es ist zum
Beispiel hinreichend, zu einem vorigen duͤnnen Blaͤttchen bloß ein
Blatt von ganz feinem Papier hinzuzufuͤgen, um einen merklichen Unterschied
in der Erniedrigung der Temperatur zu finden. Der geringste Unterschied in der
Qualitaͤt des dazwischen gelegten duͤnnen Koͤrpers zeigt sich
durch die Veraͤnderung, welche in dieser Erniedrigung der Temperatur Statt
findet, und diese Erniedrigung ist verhaͤltnißmaͤßig sehr
betraͤchtlich, wenn die Art der Substanz sehr verschieden wird; wenn man zum
Beispiel einen Stoff aus Leinwand durch Flanell oder Tuch oder auch nur ein
duͤnnes Tuch durch ein sehr dikes ersezt: diese Unterschiede waren leicht
vorauszusehen, weil sie uns schon durch das Zeugniß unserer Sinne angezeigt werden;
das Instrument aber dient nicht nur dazu, sie sehr empfindlich bei dem Messen zu
machen, sondern es leistet noch mehr, es gibt, was sehr wichtig ist, constante
Anzeigen, die immer wieder ebenso hervorkommen, wenn man dieselben Versuche
wiederholt. Es ist zu bemerken, daß diese Bestaͤndigkeit in den Resultaten
wesentlich von der Vollstaͤndigkeit der durch den Druk des Queksilbers auf
die duͤnne und biegsame Haut, welche es festhaͤlt, hervorgebrachten
Beruͤhrung abhaͤngt. Diese Bedingung, eine der Hauptschwierigkeiten
bei der Zusammensezung dieses neuen Instrumentes, war durchaus noͤthig, wenn
seine Anzeigen regelmaͤßig und auf eine große Anzahl von Koͤrpern
anwendbar seyn sollten, denn ohnedieß haͤtte man die verschiedenen Substanzen
nicht unter einander vergleichen koͤnnen, es sey denn, daß man ihnen
vorlaͤufig eine hinreichend ebene und gleichfoͤrmige
Oberflaͤche ertheilt haͤtte, damit die Beruͤhrung des
Instrumentes auf einer großen Anzahl von Puncten Statt gefunden haͤtte.
Ich habe nun gezeigt, wie man mit dem neuen Beruͤhrungs-Thermometer auf
eine annaͤhernde Weise das specifische Leitungsvermoͤgen messen
kann.
Bei diesen Versuchen muß die Substanz, welche man pruͤfen will, als ein
duͤnnes Blatt angewandt werden; man gibt ihr eine sehr kleine Dike, um den
Einfluß ihrer specifischen Waͤrme auf den Gang der Erkaͤltung zu
vermeiden.
Dasselbe Instrument dient auch, um die Beruͤhrungswaͤrme eines Koͤrpers
anzuzeigen, und mißt gewissermaßen die Empfindung von Waͤrme oder
Kaͤlte, welches diese Beruͤhrung erzeugt.
Fuͤr Versuche dieser Art braucht man nur die Temperatur dieses Instrumentes
auf die von mir angegebene Weise zu erhoͤhen, und es sodann auf eine dike
Masse der Substanz zu stellen, welche man pruͤfen will.
Man bemerkt die Anzahl der Grade, um welche sich die Temperatur waͤhrend einer
gegebenen Zeit, zum Beispiel fuͤnf Minuten, erniedrigt.
Diese Art, das Beruͤhrungsthermometer anzuwenden, hat auf merkwuͤrdige
Resultate gefuͤhrt. Die Verschiedenheiten in der Erniedrigung der Temperatur
sind fuͤr verschiedene Koͤrper sehr groß.
So habe ich zum Beispiel das erhizte Thermometer auf eine Eisenmasse von 8°
gestellt; ich stellte es sodann auf eine Masse von Sandstein von gleicher
Temperatur; der Unterschied in der Erkaͤltung betrug in beiden Faͤllen
ungefaͤhr fuͤnf Grade seit der zweiten Minute. Dieser Unterschied ist
noch merklicher, wenn man das Eisen mit dem Ziegelstein, und noch bei weitem mehr,
wenn man es mit dem Holze vergleicht.
Diese Versuche sind außerordentlich leicht: es ist nur noͤthig, daß die
Massen, auf welche man das Thermometer sezt, dieselbe Temperatur haben.
Die bei dieser Art von Versuchen hervorgebrachte Wirkung ist sehr verwikelt, und um
sie genau auszudruͤken, muͤßte man alle Umstaͤnde, welche sie
modificiren, beruͤksichtigen. Man koͤnnte sich jedesmahl, so oft man
auf diese Art Koͤrper, deren specifische Waͤrme man kennt, behandeln
wuͤrde, eine hinreichend genaue Kenntniß ihrer eigenthuͤmlichen
Leitungsfaͤhigkeit verschaffen.
Der Gebrauch des Beruͤhrungsthermometers gibt im Allgemeinen nur
annaͤhernde Werthe ihrer Leitungsfaͤhigkeit; es gibt aber eine sehr
große Anzahl von Koͤrpern, wie zum Beispiel die Ziegel, Steine, das Holz und
die Zeuge, wofuͤr diese Masse hinreichend sind.
Wir haben bemerkt, daß man noch ein anderes Instrument anwenden kann, um die
Leitungsfaͤhigkeit zu messen. Diese zweite Art zu experimentiren, macht die
Wirkungen noch merklicher; sie erfordert aber viel mehr Sorgfalt: anfangs hoffte
ich, daß es mir moͤglich seyn wuͤrde, einige dieser lezteren
Beobachtungen in Gegenwart der Akademie zu wiederholen; aber die außerordentliche
Schwierigkeit, sie in einer veraͤnderlichen und bewegten Atmosphaͤre
anzustellen, noͤthigt mich darauf zu verzichten; ich beschraͤnke mich
darauf, das Princip und einige Resultate anzugeben.
Dieser Versuch besteht darin, daß man, nicht wie bei dem ersteren, die auf einander folgenden
Erniedrigungen der Temperatur eines Koͤrpers, welchen man zuerst erhizt hat,
beobachtet, sondern die endliche und bestaͤndige Temperatur, welche die
Waͤrme hervorbringt, wenn sie verschiedene Koͤrper durchdringt.
Ich habe mir vorgenommen, diesen endlichen Zustand hervorzubringen, um daraus das Maß
der specifischen Leitungsfaͤhigkeiten abzuleiten, und bin bei der Einrichtung
des zu diesen Versuchen erforderlichen Apparates, durch einen sehr geschikten
Physiker unterstuͤzt worden, naͤmlich den Hrn. Colladon aus Genf, dessen Arbeiten die Akademie schon gekroͤnt hat,
und der mit Hrn. Sturm den im lezten Jahre fuͤr
die mathematische Physik ausgeschriebenen Preis gewann. Er war nicht nur so
guͤtig, die Verfertigung des Instrumentes zu leiten und seine Dimensionen zu
bestimmen, sondern er hat daran auch eine besondere Einrichtung angebracht, welche
ihm eigenthuͤmlich ist. Sie besteht darin, ein Queksilberkissen dazwischen zu
bringen, welches die Beruͤhrung der Stuͤze mit allen Puncten der
Huͤlse bestimmt.
Diese Methode, einen endlichen Zustand des Gleichgewichts hervorzubringen, hat den
Vortheil, Resultate zu geben, welche nicht von der specifischen Waͤrme der
dazwischen gelegten Substanz abhaͤngen. Man bringt diese Substanz oder
Huͤlse zwischen zwei Gefaͤße, wovon das eine untere, A, bestaͤndig auf der Temperatur von 100°
(Ctsk.) erhalten wird, waͤhrend das obere auf die Huͤlse gesezte
Gefaͤß, B, auf der Temperatur des schmelzenden
Eises erhalten wird.
Die Leitungsfaͤhigkeit der Einkleidung bestimmt die Waͤrmemenge, welche
aus dem Gefaͤße, A, in das Gefaͤß, B, geht; auf dem Boden des oberen Gefaͤßes, B, ist ein sehr empfindliches Luftthermometer, welches
die hervorgebrachte Wirkung mißt. Diese Luft, welche sich erhizt, ist in dem
metallischen Gehaͤuse, c, c, c', c', enthalten,
dessen unterer Theil, c, c, in Beruͤhrung mit dem
100° heißen Queksilberkissen ist, waͤhrend der andere Theil, c', c', in Beruͤhrung mit dem schmelzenden Eise
ist.
Da nun die in dem Gehaͤuse enthaltene Luft einerseits der Einwirkung des Eises
und andererseits derjenigen eines auf 100° erhizten Koͤrpers ausgesezt
ist, so nimmt sie eine fixe mittlere Temperatur an. Der gefaͤrbte Index, o, des Luftthermometers bleibt stehen, wenn die
Waͤrmemenge, welche in das Thermometer durch die Huͤlse dringt, genau
derjenigen gleich ist, welche es dem Eise mittheilt. Dieses Gleichgewicht bildet
sich in einigen Secunden: es ist der endliche Zustand, um dessen Beobachtung es sich
handelte.
Die von dem Luftthermometer angezeigte fixe Temperatur haͤngt offenbar von der
Temperatur der dazwischen gelegten Substanz ab. Wenn dieser duͤnne
Koͤrper der freien Mittheilung der Waͤrme sehr wenige Hindernisse in den Weg
legt, so ist die endliche Temperatur des Luftthermometers viel groͤßer, als
wenn die Waͤrme nur sehr schwer die dazwischen gelegte Huͤlse
durchdringt. In allen Faͤllen findet ein sehr einfaches Verhaͤltniß
zwischen der erlangten Temperatur und der Leitungsfaͤhigkeit des dazwischen
gelegten Koͤrpers Statt. Um dieses Verhaͤltniß auszudruͤken,
bezeichnen wir wie bei den vorhergehenden Versuchen durch h die Waͤrmemenge, welche waͤhrend der Zeit 1 von der Masse
der Stuͤze in das Innere des Luftthermometers durch die Einheit der
Oberflaͤche der Huͤlse dringen wuͤrde, wenn die Differenz
zwischen der Temperatur der Luft und des Eises 1 waͤre; und durch H die Waͤrme, welche waͤhrend der
Zeit-Einheit die Einheit der Oberflaͤche durchdringen wuͤrde,
indem sie von der oberen Oberflaͤche c'c'
des Luftthermometers in die darunter befindliche Eismasse gehen wuͤrde, wenn
die Differenz zwischen der Temperatur der Luft und des Eises 1 waͤre.
Textabbildung Bd. 29, S. 170
sind also einer- und andererseits die
Waͤrmemengen, welche waͤhrend des Augenbliks dt aus der Stuͤze in die Luft durch die
Oberflaͤche b der Huͤlse ausfließen oder
von der Luft in das Eis durch den Umfang S der oberen
Oberflaͤche der Thermometer-Capacitaͤt hindurchgehen. (Um den
Ausdruk allgemeiner zu machen, bezeichnet man durch M
die fixe Temperatur der Stuͤze, und durch N die
fixe Temperatur der kalten Masse, in welche die Waͤrme ausfließt.) Nun ist
aber das Gleichgewicht hergestellt, sobald die von der Stuͤze mitgetheilte
Waͤrme genau die Waͤrme ausgleicht, welche die Capacitaͤt des
Thermometers dem Eise mitheilt; man hat also diese Gleichung
Textabbildung Bd. 29, S. 170
und das Verhaͤltniß
bh/Hs + (α – H)/Mα.
Es wird also hinreichend seyn, α zu messen, um das
Verhaͤltniß h/H der beiden relativen
Leitungsfaͤhigkeiten h und H, naͤmlich die gegenseitige Leichtigkeit des Ueberganges der
Waͤrme von der Stuͤze in die Capacitaͤt des Thermometers, oder
von dieser Capacitaͤt in die umgebende Masse zu kennen. Das
Verhaͤltniß b/s muß als bekannt betrachtet
werden; es veraͤndert sich nicht, wenn man die erste Huͤlse, welcher
der Coëfficient h zukommt, durch eine zweite
Huͤlse ersezt, welcher ein anderer Coëfficient h zukommt. Ebenso verhaͤlt es sich mit dem Coëfficient H, welcher sich gleich bleibt. Wenn man verschiedene
Koͤrper mit demselben Instrument pruͤft, wird die Temperatur
α durch das Luftthermometer gemessen, welches auf
verschiedene Art eingerichtet seyn kann. Ich gebe hier nicht die auf dieses
Thermometer sich beziehende Berechnung, weil diese Berechnung, welche
uͤbrigens mit gar keiner Schwierigkeit verbunden ist, nach der
gewaͤhlten Construction desselben verschieden ist; in allen Faͤllen,
glaube ich, hat man dieses Instrument so eingerichtet, daß es sehr empfindlich wird,
und die Bedingungen genau untersucht, welche die Stellung des Index bestimmen. Was
die respectiven Werthe betrifft, die man M und N beilegen kann, und welche wir anfangs zu 1 und 0
angenommen haben, so haben wir durch wiederholte Versuche gefunden, daß die
Beobachtungen leichter und die Resultate bestaͤndiger werden, wenn die Zahlen
M und N weniger
differiren, zum Beispiel, wenn man M = 4/5 (80
Centesimalgrade) und N = (15 Cents. Grade) macht.
Wenn man nach und nach dasselbe Verfahren mit duͤnnen Koͤrpern
verschiedener Natur wiederholt, wird man verschiedene Resultate erhalten, je nach
der Natur der Substanzen, welche die Waͤrme durchdringt. Die Erfahrung hat
uns in der That gelehrt, daß diese Verschiedenheiten außerordentlich groß sind. Wenn
man nur ein einfaches Blatt Briefpapier, von dem duͤnnsten, welches man
erhalten kann, noch hinzufuͤgt, bringt es in der Stellung des Index einen
Unterschied von 20 Linien hervor. Fuͤgt man zu dem ersten Blatt noch ein
zweites von demselben Papier, so verruͤkt man den Inder noch um 25 Linien
mehr. Diese Verruͤkung, welche, wie bereits bemerkt wurde, in einigen
Secunden geschieht, wird sehr groß, wenn die dazwischen gelegte Substanz schwer von
der Waͤrme durchdringlich ist; sie betraͤgt fuͤr gewisse
Substanzen mehr als 100 Linien.
Wir haben sowohl mit dem einen als mit dem anderen Instrument eine sehr große Anzahl
verschiedener Substanzen gepruͤft, naͤmlich alle wichtigeren Arten von
Geweben, Haͤuten, Pelzfuttern, oder von Substanzen wie das Glas, der Glimmer,
die Blaͤtter verschiedener Metalle und die Resultate fuͤr jede
Substanz, je nach ihrem Gefuͤge oder ihrer besonderen Natur, verschieden
gefunden.
Wenn man die mittelst dieses lezteren Instrumentes (welches man
Beruͤhrungsthermoskop (thermoscope de contact)
nennen kann) erhaltenen Resultate mit denjenigen vergleicht, welche man mit dem
zuerst beschriebenen Instrument erhaͤlt, so bemerkt man, daß die durch das
Thermoskop so merklich gemachten Unterschiede auch bemerkbar werden, wenn man die
allmaͤhliche Erkaltung des Beruͤhrungsthermometers beobachtet; nur
werden mit dem ersteren Instrumente die Unterschiede nach der Zeit gemessen, und man
kann sie so auf eine eben so bequeme als genaue Weise bestimmen, wie vermittelst des
zweiten Apparates; die
Resultate sind weniger auffallend, aber auch bestaͤndiger, und da dieses
zweite Thermometer außerordentlich einfach construirt und leicht zu handhaben ist,
so eignet es sich sehr fuͤr den allgemeinen Gebrauch.
Dieses Instrument kann zu einer Menge interessanter oder nuͤzlicher
Untersuchungen dienen; es zeigt natuͤrliche Eigenschaften an, die man durch
den Gebrauch der Sinne allein nicht haͤtte entdeken koͤnnen: so hat es
mir zum Beispiel gedient, um die Richtigkeit einer Thatsache zu erweisen, die mir
schon lange wahrscheinlich war: daß naͤmlich die Waͤrmemenge, welche
durch mehrere auf einander gelegte duͤnne Koͤrper streicht, nach der
Reihe, in welcher man dieselben auf einander legt, verschieden ist; so habe ich
folgenden Versuch angestellt: ich habe das Beruͤhrungsthermometer auf die
marmorne Stuͤze gestellt, wovon es durch zwei Tuchscheiben getrennt war; die
Waͤrme mußte also durchdringen: Haut, Tuch, Tuch, Marmor. Nachdem ich die
allmaͤhliche Erkaltung beobachtet hatte, legte ich eine Kupferscheibe von der
Dike eines duͤnnen Blattes Papier auf den Marmor unter die beiden
Tuchscheiben; die Erkaͤltung des Thermometers innerhalb einer gegebenen Zeit
war geringer, als bei dem vorhergehenden Versuche; das Kupferblatt wurde sodann
zwischen die beiden Tuchscheiben gelegt; die Erkaͤltung war in derselben Zeit
gerade so groß, als wenn man, wie bei dem ersten Versuche, das Kupferblatt
weggelassen haͤtte.
Endlich legte ich die Kupferscheibe auf die Tuchscheiben unmittelbar unter die Haut
des Beruͤhrungsthermometers: in diesem Falle durchdrang die Waͤrme die
Huͤlsen in folgender Ordnung: Haut, duͤnnes Kupfer, Tuch, Tuch,
Marmor. Das Thermometer fiel tiefer, als wenn man die Kupferscheibe weggelassen
haͤtte. So erleichtert dieses Kupferblatt, wenn es dazwischen gelegt wird,
die Fortpflanzung der Waͤrme der Haut zu dem Tuch, und vermindert die
Fortpflanzung der Waͤrme des Tuches zu dem Marmor. Dieses sind die Wirkungen,
welche man waͤhrend der 10 ersten Minuten beobachtet; Resultate, welche nicht
einem gleichen Zeitraum entsprechen, darf man nicht mit einander vergleichen.
Ich werde nicht noch mehrere von den neuen Versuchen anfuͤhren, welche mit
diesen Instrumenten angestellt worden sind. Das Beruͤhrungsthermometer muß
als eine mit ihrem Thermometer versehene Hand betrachtet werden. Diese Versuche
koͤnnen die mathematische Theorie der Waͤrme nicht bereichern; aber es
verdient alles, was sich auf die technischen Kuͤnste und den allgemeinen
Nuzen bezieht, die Aufmerksamkeit der Akademie. Obige Beobachtungen sind in
wissenschaftlicher Hinsicht eben so interessant als diejenigen, welche zur
Bestimmung der specifischen Waͤrme verschiedener Koͤrper dienten: sie machen uns genauer
mit solchen physischen Eigenschaften bekannt, welche die Sinne zwar anzeigen, die
sie aber nicht messen: der Zwek der Instrumente ist uͤberhaupt auch dieser,
daß sie unser intellectuelles Vermoͤgen durch die Vervollkommnung unserer
Sinne verstaͤrken sollen.
Die Theorie der Waͤrme, in dieser Hinsicht den dynamischen Theorieen
vergleichbar, ist eben so gut auf das Weltsystem als auf die gewoͤhnlichsten
Verrichtungen des Lebens anwendbar; die Theorie hat uns unter anderem mit der
endlichen Wirkung bekannt gemacht, welche das Strahlen der Fixsterne hervorbringt.
Sie hat uns gelehrt, daß die Temperatur des Raumes, welchen unser Planetensystem
einnimmt, sehr nahe 40 Reaumur'sche Grade kaͤlter, als die Temperatur des
schmelzenden Eises ist. Dieselbe Theorie dient auch, um die erwaͤrmende Kraft
verschiedener Kleider, Deken, Gewebe zu messen und gestattet uns, noch unbekannte
natuͤrliche Eigenschaften der Koͤrper zu entdeken.
Ich will nun demjenigen, was ich uͤber diese neuen Versuche uͤber die
Leitungsfaͤhigkeit duͤnner Koͤrper gesagt habe, noch eine
theoretische Bemerkung uͤber die Beobachtungen beifuͤgen, welche dazu
dienen koͤnnen, um die Eigenschaften der Koͤrper zu messen.
Wenn die Substanzen, welche man pruͤfen will, sehr gute Waͤrmeleiter
sind, wie zum Beispiel die Metalle, bestimmt man ihr Leitungsvermoͤgen auf
die Art, daß man die fixen Temperaturen einer prismatischen Stange beobachtet, deren
Ende auf einer ziemlich gleichen Temperatur erhalten wird. Der Versuch hat gezeigt,
daß dieser endliche Zustand demjenigen entspricht, welchen die Theorie ergibt. Die
beobachteten Temperaturen bilden in der That eine abnehmende Reihe, woraus man den
numerischen Werth der Leitungskraft abgeleitet hat; man kann aber diesen Ausdruk
nicht auch auf solche Koͤrper, deren Leitungskraft sehr schwach ist, wie bei
dem Marmor, oder auf die Metalle anwenden, welche die Waͤrme leicht
durchdringt. Der Grund dieses Unterschiedes ist dieser: in den Koͤrpern,
welche die Waͤrme schlecht leiten, erlangen und erhalten die Molecule, welche
auf demselben auf der Achse des Prismas senkrechten Durchschnitt liegen,
bestaͤndige, ungleiche Temperaturen, welche sich schnell von der Achse bis
zur aͤußern Oberflaͤche vermindern; in den Koͤrpern aber,
welche bessere Waͤrmeleiter sind, wie das Gold, Platin, Kupfer, nehmen alle
Puncte desselben senkrechten Durchschnittes auf die Achse, ziemlich dieselbe
Temperatur an. Die Thatsache ist leicht zu begreifen, man koͤnnte sie
vorlaͤufig als bekannt annehmen; die analytische Theorie erklaͤrt sie
aber auch vollkommen, wie es der allgemeine Ausdruk zeigt, den ich schon
fruͤher fuͤr die gleichmaͤßige Bewegung der Waͤrme in
einem rechtwinklichen Prisma von beliebiger Dike aufgestellt habe; denn dieselbe
Aufloͤsung lehrt, daß wenn die eigenthuͤmliche
Leitungsfaͤhigkeit sehr schwach, oder die Dike der Stange sehr groß ist, die
Puncte von demselben normalen Durchschnitte sehr verschiedene Temperaturen haben. In
diesem Falle enthaͤlt der Ausdruk der Temperatur nicht nur die Entfernung von
dem Ursprung, sondern auch die Coordinaten jedes Punctes des Durchschnittes.
Man muͤßte also von dieser Formel Gebrauch machen, um die specifische
Leitungsfaͤhigkeit derjenigen Koͤrper zu bestimmen, welche diese
Eigenschaft nur in geringem Grade haben. Die Formel, welche man in den
Faͤllen, wovon es sich hier handelt, gebrauchen muß, ist die auf S. 406
meiner Théorie de la chaleur, und nicht die auf
S. 65 desselben Werkes. Der bemerkte Unterschied geht ausdruͤklich aus der
allgemeinen Aufloͤsung hervor. Man braucht nur der Groͤße y den Werth o in der Formel
von v (S. 400) zu geben, und in Beziehung auf z zwischen den Graͤnzen – l und + l zu integriren, um
einen der mittleren Temperatur proportionalen Werth zu finden.
Man muß vorzuͤglich die Gleichung tang. ε =
hl/k und die
Construction, wodurch man die Wurzeln dieser hoͤheren Gleichung
erfaͤhrt, beruͤksichtigen. Man sieht, daß der Werth der Temperatur das
Product hl
/k enthaͤlt, so daß, wenn die
eigenthuͤmliche Leitungsfaͤhigkeit k als
sehr schwach angenommen wird, dieser Fall sich nicht von demjenigen unterscheidet,
wo die halbe Dike des Prismas sehr groß ist; daraus folgt, daß wenn man den
Coëfficient k, das Maß der Durchdringbarkeit, als
sehr klein annimmt, die Temperaturen nicht wie die Glieder einer abnehmenden Reihe
abnehmen, was nur bei einer unendlich großen Entfernung von dem Anfang (Ursprung der
Waͤrme) Statt finden wuͤrde; die Temperaturen fallen anfangs sehr
schnell von dem Ursprung angefangen. Man sieht aus der, Seite 410 des
angefuͤhrten Werkes gegebenen numerischen Berechnung, daß man sich nur von
dem Anfange der Haͤlfte der Dike der Stange zu entfernen braucht, damit die
Temperatur des ersten Punctes sich auf 1/50tel ihres Werthes reducirt. Alle
Beobachtungen stimmen mit den so eben angefuͤhrten theoretischen Resultaten
uͤberein; sie zeigen, daß wenn die eigenthuͤmliche
Leitungsfaͤhigkeit sehr groß ist, die beobachteten Temperaturen abnehmen, wie
die Glieder einer abnehmenden Reihe; wenn aber bei solchen Koͤrpern, deren
Leitungsvermoͤgen sehr gering ist, der Versuch Welche gaͤbe, welche
durch eine Exponentenreihe vorgestellt werden koͤnnen, dann wuͤrde die
Beobachtung nicht mit der Theorie uͤbereinstimmen; in diesem Falle hat der
Ausdruk eine solche Form, daß man die untergeordneten Glieder nicht mehr
vernachlaͤssigen kann. Uebrigens sind in eben diesem Falle die beobachteten
Temperaturen zu gering, als daß man daraus das Leitungsvermoͤgen mit
Genauigkeit ableiten koͤnnte. Die Verfahrungsweisen, welche eine genaue
Theorie als die am meisten geeigneten bezeichnet, um das Leitungsvermoͤgen
solcher Koͤrper zu messen, welche diese Eigenschaft nur in geringem Grade
besizen, unterscheiden sich sehr von denjenigen, welche fuͤr die metallischen
Substanzen anwendbar sind; sie wuͤrden darin bestehen, die entweder
gleichfoͤrmige oder veraͤnderliche Bewegung der Waͤrme in
Gefaͤßen aus verschiedenen Substanzen zu beobachten, deren Dike man
verschieden abaͤndern muͤßte. Diese analytische Untersuchung steht in
Beziehung mit derjenigen, welche ich vor einigen Jahren in einem Mémoir
uͤber die Temperatur der Wohnungen abhandelte.
Beschreibung der beiden Instrumente, welche in der Abhandlung
des Hrn. Fourier angefuͤhrt wurden.
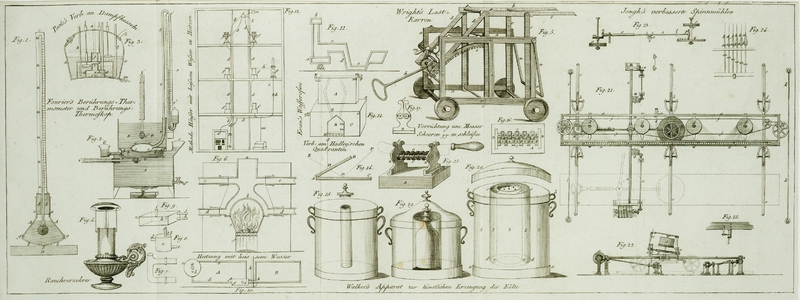
Fig. 1.
Durchschnitt des Beruͤhrungs-Thermometers.
A, A, kegelfoͤrmiges Gefaͤß aus sehr
duͤnnem Eisen, mit Queksilber beinahe voll gefuͤllt; eine Rinne, g, g, um den unteren Rand, dient zum Festbinden der
Huͤlle, die das Queksilber enthaͤlt; oben im Kegel ist eine Oeffnung
mit einer kurzen Roͤhre, a, a, von 7–8
Linien im Durchmesser.
l, l, ist ein Korkpfropfen, der in diese Roͤhre
paßt. Er dient zur Befestigung des Thermometers, c, c,
in dem Gefaͤße, und hilft dasselbe in gehoͤriger Hoͤhe
erhalten.
Die Kugel des Thermometers, c, muß einige Linien
uͤber der Basis des Kegels, und ganz in das Queksilber des Gefaͤßes
eingesenkt seyn.
Die Huͤlle, b, b, b, muß eine weiche, geschmeidige
weiche, duͤnne Haut seyn. Die oben erwaͤhnten Versuche
uͤberzeugten uns, daß diese Haut sehr gut dazu taugt, weil die Haut die
Waͤrme besser, als jeder andere Stoff von gleicher Dichtigkeit leitet.
Man muß dafuͤr sorgen, daß diese Haut nicht schmuzig ist und nicht zu sehr
erhizt wird.
Wenn man sich dieses hoͤchst einfachen Werkzeuges bedienen will,
verfaͤhrt man auf folgende Weise.
Nachdem der Koͤrper, oder das duͤnne Plaͤttchen, mit welchem man
den Versuch anstellen will, auf einen marmornen Untersaz von der Temperatur des
Zimmers, in welchem man arbeitet, gestellt wurde, erhizt man das
kegelfoͤrmige Gefaͤß, indem man dasselbe auf ein Oefchen oder auf
irgend einen anderen erhizten Koͤrper stellt, und wartet, bis die Temperatur
sich auf 46 oder 47° gehoben hat. In dem Augenblike, wo das Thermometer
45° weiset, stellt man dasselbe auf die Huͤlle, und beobachtet
mittelst einer Uhr den Augenblik, wo es auf 40° sinkt, und bemerkt von Minute zu Minute
den Gang bis zur fuͤnften.
Wenn man den Versuch mit demselben Koͤrper wiederholt, und die Stelle
desselben auf dem Marmor wechselt, erhaͤlt man immer dasselbe Resultat, wenn
anders die Temperatur des Zimmers dieselbe blieb.
Wenn man sich dieses Instrumentes bedienen wollte, um genaue Versuche uͤber
die Leitungskraft steifer Blaͤttchen anzustellen, muͤßte man diese
nicht auf eine marmorne Unterlage stellen, wo die Beruͤhrung nicht vollkommen
waͤre, sondern auf ein aͤhnliches Queksilberkissen, wie jenes im
folgenden Apparate.
Fig. 2. Durchschnitt des
zweiten Apparates, oder des Beruͤhrungs-Thermoskopes.
A, wuͤrfelfoͤrmiges Gefaͤß aus
duͤnnem Kupfer; es ist oben geschlossen und ganz mit Wasser voll
gefuͤllt. Das Wasser wird mittelst eines Trichters, e, voll gefuͤllt. Der Hahn, r, dient
zur Leerung des Gefaͤßes.
Auf dem Dekel ist eine kreisfoͤrmige Kapsel, v, v,
v, aus duͤnnem Bleche aufgeloͤthet, welche ein kleines
erwaͤrmtes Queksilberbad enthaͤlt. Dieses Queksilber dient statt des
Kissens mittelst der Huͤllenhaut, b, b, b, die es
ganz und gar bedekt. Man bindet diese Huͤlle rings um die Kapsel, und der
Ring, dessen Durchschnitt man in, a, a, sieht,
haͤlt ihn gespannt. Das Queksilber, das gegen diese Huͤllenhaut
druͤkt, gibt ihr ganz die Gestalt eines convexen Kissens.
Man bringt das Queksilber in die Kapsel, und hebt es aus derselben mittelst eines
Naͤpfchens, g, und einer an der Seite
angebrachten eisernen Rohre, g, g. Die Hoͤhe des
Queksilbers in dem Naͤpfchen bestimmt die Spannung des Kissens.
Unter dem Gefaͤße, A, ist eine kleine Lampe, die
das Wasser in einer bestimmten Temperatur erhaͤlt, z.B. auf 100 oder auf
60°. Das innere Thermometer, i, dient zur Anzeige
der Temperatur, folglich auch zur Anzeige der Temperatur des Queksilberbades.
B, ist das obere Gefaͤß, welches Eis, oder noch
besser Wasser von einer bestimmten bleibenden Temperatur enthaͤlt, die wenig
uͤber jener des Zimmers, in welchem man arbeitet, erhaben ist. Das kleine
Thermometer, i, zeigt die Temperatur dieses Wassers
an.
Im Grunde des Gefaͤßes, B, befindet sich eine
metallne Hoͤhle, die man bei, c, c, c', c', im
Durchschnitte sieht. Dieß ist die Kugel des anzeigenden Thermoskopes. Die obere
Haͤlfte, c', c', springt am Boden des
Gefaͤßes, B, vor, und ist mit dem Eise oder mit
dem kalten Wasser in Beruͤhrung; die untere Haͤlfte ruht auf dem
erwaͤrmten Queksilberkissen.
Die gekruͤmmte Roͤhre, t, t, t', t', die
mit dieser Hoͤhlung in Verbindung steht, macht die Ausdehnungen der Luft
sichtbar, welche in dieser Hoͤhlung enthalten ist.
Zu diesem Ende ist der obere Theil dieser Roͤhre, t,
t, mit einer gefaͤrbten Fluͤssigkeit gefuͤllt, die
sich senkt, wenn die Luft in der Hoͤhlung sich erhizt und sich ausdehnt. Um
den Versuch anzustellen, hebt man das obere Gefaͤß, B, ab, legt auf das Kissen eine Scheibe aus dem Koͤrper, den man
pruͤfen will, und sezt das obere Gefaͤß wieder auf. Die untere
Oberflaͤche, c, c, des Luftraumes ist von dem
Kissen mittelst des Koͤrpers abgeschieden und erhaͤlt weniger
Waͤrme, und folglich nimmt die darin enthaltene Luft eine mittlere oder
weniger hohe Temperatur an. Der Zeiger, o, bleibt auf
einem hoͤheren Puncte.
Da dieser Apparat sehr schnell und deutlich zeigt, so kann er auch bei
oͤffentlichen Versuchen dienen.
Tafeln