| Titel: | Ueber den Regulator (Graduater ) beim Spinnen und Vorspinnen der Baumwolle, des Worsted, des Flachses etc. etc. Von J. Rayner, Esq. |
| Fundstelle: | Band 32, Jahrgang 1829, Nr. XLIV., S. 240 |
| Download: | XML |
XLIV.
Ueber den Regulator (Graduater
Der Hr. Verfasser sagt am Ende seiner Abhandlung: „er faͤnde es
uͤberfluͤssig, eine Apologie fuͤr das neue Wort
„Graduater zu schreiben, da es
ihm das geeignetste zu seyn scheint, das er waͤhlen konnte, und
keiner weiteren Erklaͤrung bedarf.“ Wir glauben in der
deutschen Sprache das bei uns bereits eingebuͤrgerte Wort
„Regulator“ brauchen
zu koͤnnen.
) beim Spinnen und Vorspinnen der Baumwolle, des Worsted, des Flachses etc. etc.
Von J. Rayner, Esq.
Aus dem London Journal of Arts. Jaͤner 1829. S.
182.
Mit Abbildungen auf Tab.
VI.
Rayner, über den Regulator beim Spinnen und Vorspinnen der
Baumwolle, des Worsted, des Flachses etc.
Sir Richard Arkwright hat durch seine Methode, mittelst
Walzen zu spinnen, und durch das Verfahren bei demselben, welches Er erfunden hat,
unserem Lande eine Quelle fuͤr Industrie eroͤffnet, die die
eintraͤglichste geworden ist, welche es bisher besessen hat. Die eben so
zierlichen als maͤchtigen Spinn-Maschinen, die in unseren großen
Spinn-Muͤhlen in Lancashire und Yorkshire in Menge errichtet sind,
haben die groͤßten mechanischen Genies unseres Landes in Thaͤtigkeit
gesezt.
Da das Vorgespinst oder das Garn in einem gegebenen Verhaͤltnisse von den
Walzen abgegeben, und, nachdem es gedreht wurde, auf cylindrischen Walzen mittelst
der Spindel und der Fliege aufgewikelt oder aufgewunden wird, so ward es nothwendig,
die Geschwindigkeit der Spule so zu reguliren, daß waͤhrend des ganzen
Auswindens auf die Spule der Faden immer eine gleichfoͤrmige Spannung
erhaͤlt: dieß ist offenbar bei weichem und feinem Vorgespinste und bei sehr
feinem Garne noch weit nothwendiger.
Die Anfangs angewendeten Regulatoren waren roh und unvollkommen: Erfahrung und
naͤhere Vertrautheit mit dem Gegenstande veranlaßte von Zeit zu Zeit
verschiedene Erfindungen zur vollkommneren Erreichung dieses Zwekes, d.h., zu einer
solchen Regulirung der Geschwindigkeit der Spule, daß immer das gehoͤrige
Verhaͤltniß derselben nach der Zunahme des Umfanges der Spule durch die auf
einander auf derselben nach und nach waͤhrend des Spinnens aufgewundenen
Lagen des Vorgespinstes und Garnes unterhalten wird.
Meine Absicht ist hier nicht alle diese verschiedenen Erfindungen zu beschreiben;
denn so verschieden sie auch in ihrer Ausfuͤhrung seyn moͤgen, ist
doch der Zwek bei allen derselbe, und sie gehen von demselben Grundsaze aus. Ein
Stuͤk eines Kegels schien bisher der beliebteste Regulator, und wurde
haͤufiger als jeder andere angewendet. Ich will daher meine Beobachtungen
vorzuͤglich auch auf diesen anwenden.
Da ich mich seit mehreren Jahren mit Verfertigung von Spinnmaschinen
beschaͤftige, so bot sich dieser Gegenstand mir unter verschiedenen
interessanten Ansichten dar, und veranlaßte mich endlich diesen Gegenstand in
Hinsicht auf Auffindung einer allgemeinen Regel zu untersuchen, die sich auf jeden
gegebenen Fall anwenden ließe. Ich erwarte, daß man folgende Lehrsaͤze auf
richtige Grundsaͤze gebaut und auf den vorliegenden Fall gehoͤrig
angewendet finden wird.
Der erste Schritt, worauf es bei dieser Aufgabe ankommt, mag vielleicht schwierig
scheinen, und mehrere Betrachtungen, die man bei Aufloͤsung derselben zu
beruͤksichtigen hat, machen denselben verwikelt: man hofft indessen, daß die
Methode, nach welcher dieser Gegenstand hier behandelt wurde, die allgemeinen
Grundsaͤze, nach welchen bei solchen Fragen verfahren werden muß, deutlicher
und faßlicher machen wird.
Die allgemeinen Theoreme mit den Beweisen und den erlaͤuternden Beispielen
zeigen, wie leicht sich dieselben auf jeden einzelnen Fall anwenden lassen. Dem
praktischen Mechaniker gewaͤhren sie ein leichtes Mittel zur Berechnung, und
diejenigen, die mit den hoͤheren Zweigen der Mechanik bekannt sind, werden
nicht ohne Vergnuͤgen die innige Verbindung wahrnehmen, in welcher die
abstrakte Wissenschaft mit der praktischen und operativen Mechanik steht.
Diese Lehrsaͤze beziehen sich auf ein Kegelstuͤk, welches durch ein
gewoͤhnliches Laufband auf einen Cylinder wirkt. Man nimmt an, daß die
Maschine so eingerichtet ist, daß fuͤr die erste Geschwindigkeit der Spule
bei dem Vorspinnen oder Spinnen so genau als moͤglich gesorgt ist. Folgende
Umstaͤnde muͤssen ferner als Data fuͤr die Berechnung mit aller
Genauigkeit bestimmt werden.
1) Durchmesser der Speisungs-Walzen, die das Vorgespinst abgeben.
2) Die Menge des Garnes oder die Zahl der Umdrehungen, welche die Spindel gegen Eine
Umdrehung der Speisungs-Walzen macht.
3) Die Dike des Vorgespinstes oder des Garnes, welches gesponnen werden soll.
4) Der Durchmesser der Spule, auf welcher das Vorgespinst oder Garn aufgewunden
wird.
5) Der erste Durchmesser des Kegelstuͤkes, so wie dessen Laͤnge oder
Hoͤhe, muß als bekannt angenommen werden.
6) Die Zahl der Lagen des Vorgespinstes oder Garnes, welches auf den Cylinder der
Spule aufgewunden wird, so daß man, noͤthigen Falles, die aͤußerste
Groͤße nehmen kann.
Wir wollen nun, unter obigen Voraussezungen, die allgemeinen Grundsaͤze
angeben, und die Data als Beispiele anwenden.
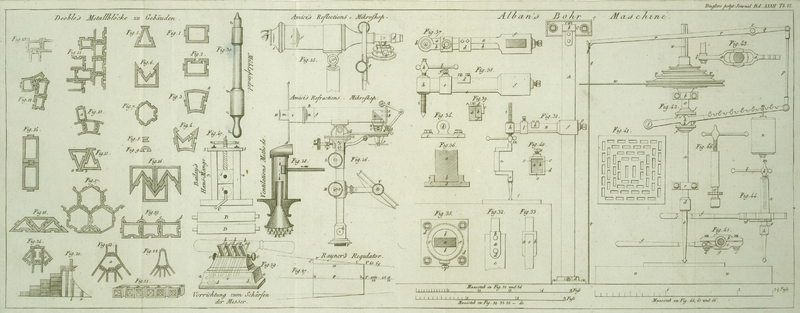
Die schwarze Linie in der Figur 27 stellt das
Stuͤk eines Kegels dar.
Es sey nun
d, der kleine Durchmesser
des Kegelstuͤkes = 6.
n, der große Durchmesser =
7,314.
v, die schiefe Seite des
Kegels = 45,69.
P, die senkrechte
Hoͤhe des Kegels = 1050/23 oder 45 15/23
= 10 die Hoͤhe oder Laͤnge des
Kegelstuͤkes.
Aus der Aehnlichkeit der Dreieke ergeben sich
nun folgende Verhaͤltnisse:
1/2 d : v : : (n –
d)/2 : (n
– d)/2 × v.
1/2 d : P : : (n –
d)/2 : (n
– d)/2 × P.
(n – d)/2 : 10 : : 1/3 d
: P, die Hoͤhe des Kegels.
Es sey nun
a der Umfang der vorderen
oder Speisungs-Walze = 3,927.
t das Garn, oder die Zahl
der Umdrehungen der Spindel gegen eine Umdrehung der vorderen Walzen.
r die doppelte Dike des
Vorgespinstes oder Garnes.
b der Umfang des
Spulen-Cylinders = 3,1416.
d der angenommene
Durchmesser des Kegelstuͤkes = P.
c der Werth einer jeden
Umwikelung oder Aufwindung, oder die Zahl der Lagen des Vorgespinstes oder
Garnes.
So erhaͤlt man
Textabbildung Bd. 32, S. 242
der Geschwindigkeit des Spulen-Cylinders; und da
Textabbildung Bd. 32, S. 243
dem zweiten Durchmesser. Aus diesen Daten ergibt sich
folgender allgemeiner Lehrsaz, um die auf einander folgenden Durchmesser des
Kegelstuͤkes unter der Bedingung zu finden, daß das Vorgespinst oder Garn so
aufgenommen wird, wie es von den Speisungs-Rollen abgegeben wurde.
Textabbildung Bd. 32, S. 243
Um diesen Lehrsaz anzuwenden, nehme man folgende bestimmte Groͤßen; z.B. t, das Garn, = 5. r, die
doppelte Dike des Vorgespinstes oder Garnes, = 1/12; d
den ersten Durchmesser, = P; c = irgend einer Zahl von 1 bis 24; so wird
Textabbildung Bd. 32, S. 243
Oben war R = 1/12. A. d. U.
dem ersten Durchmesser; und in diesem Falle wird 8 eine
gemeinschaftliche Differenz fuͤr den Dividendus, und 1 fuͤr den
Divisor; wie
12)
72
(6, erster Durchmesser
Hierzu addirt
1
8
–––––––––––––
13)
80
(6, 15, zweiter Durchmesser
Hierzu addirt
1
8
–––––––––––––
14)
88
(6, 28, dritter Durchmesser etc.
Auf diese Weise werden alle Durchmesser von 1 bis 24 gefunden,
was man hier als die aͤußersten Graͤnzen annimmt; oder
uͤberhaupt fuͤr jeden Umfang, bis zu welchem man den Cylinder der
Spule fuͤllen will. Nach diesem Lehrsaze kann jeder Durchmesser gefunden
werden, wenn man c nach dem verlangten Werthe nimmt,
z.B., als 24 fuͤr die 24igste Umwikelung der Lage des Gespinstes.
Textabbildung Bd. 32, S. 243
Um die Hoͤhe oder den Raum zu finden, uͤber welchen das Laufband auf
dem Kegelstuͤke laufen muß, erhaͤlt man aus den gegebenen Daten
Textabbildung Bd. 32, S. 244
der Hoͤhe jeder Bewegung auf der Oberflaͤche des
Kegelstuͤkes. Um diesen Lehrsaz mit den gegebenen Daten anzuwenden, wird
Textabbildung Bd. 32, S. 244
erster Divisor, und 23 und 350 gleichfoͤrmige
Differenzen fuͤr den Divisor und Dividendus, wodurch die correspondirende
Hoͤhe jeder Bewegung auf dem Kegelstuͤke gefunden werden kann, so daß
genau so viel von dem Gespinste aufgenommen wird, als von
den Speisungs-Walzen abgegeben wird.
Erster Divisor,
276)
000 (000
Hierzu addirt
23
350
––––––––––
299)
350 (1,17 der Raum, uͤber welchen die zweite
Aufwindung sich bewegt.
Hierzu addirt
23
350
––––––––––
322)
700 (2,17
23
350
––––––––––
345)
1050 (3,043 u.s.f. bis ins Unendliche.
So kann durch diesen Lehrsaz jede einzelne Bewegung des Laufbandes im
Verhaͤltnisse zu der Zahl der Umwindungen des Garnes bestimmt, und jeder
Werth fuͤr c genommen werden; z.B. fuͤr
die 24igste Umwindung
Textabbildung Bd. 32, S. 244
dem Raume, uͤber welchen die 24igste Aufwindung sich
bewegen muß. Und so wird dieser Raum fuͤr jeden Werth von c gefunden.
Bemerkungen.
Die Daten, aus welchen diese Schluͤsse gezogen sind, koͤnnen nach
Belieben abgeaͤndert, und t, d, r, a, b und n koͤnnen unter jedem Werthe, nach Belieben des
Mechanikers, genommen werden. Einige derselben muͤssen jedoch
vorlaͤufig bestimmt werden, wie oben angegeben wurde, woraus dann die Werthe
fuͤr die uͤbrigen, wie in den angefuͤhrten Beispielen sich
ergeben.
Man nimmt bei obigen Daten an, daß die Walzen, Spulen etc. alle vollkommen genau
verfertigt, und daß ihre Dimensionen genau bestimmt sind: der Faden wird als
unbiegsam betrachtet und auf den Werth von r
beschraͤnkt.
Diese Lehrsaͤze beziehen sich auf die Anwendung eines Kegelstuͤkes, das
sich auf einem Cylinder, der uͤberall vollkommen gleichen Durchmesser hat,
mittelst eines Laufbandes bewegt, und denselben in Thaͤtigkeit sezt. Wenn
meine Muße es mir gestattet, werde ich die Anwendung derselben Grundsaͤze auf
ein Doppel-Kegelstuͤk zeigen, wodurch der Laufriemen, ohne allen
anderen Spannungs-Apparat, immer in gleicher Spannung erhalten wird.
Tafeln