| Titel: | Eine Kirche, ein Wirthshaus, oder überhaupt ein Haus, in welches man öfters gehen muß, unter mehreren zerstreuten Häuser-Gruppen oder Weiler so zu stellen, daß die Einwohner dieser Häuser bei dem Hin- und Hergehen am wenigsten Zeit verlieren. |
| Fundstelle: | Band 32, Jahrgang 1829, Nr. LXXXII., S. 369 |
| Download: | XML |
LXXXII.
Eine Kirche, ein Wirthshaus, oder
uͤberhaupt ein Haus, in welches man oͤfters gehen muß, unter mehreren
zerstreuten Haͤuser-Gruppen oder Weiler so zu stellen, daß die Einwohner
dieser Haͤuser bei dem Hin- und Hergehen am wenigsten Zeit verlierenMan sieht aus dieser Aufgabe, wie sehr die goldene Regel: „Zeit
gewonnen, ist Alles gewonnen; Zeit ist das hoͤchste Gut des
Menschen“ den Englaͤnder bei allen seinen Unternehmungen
leitet. Der Englaͤnder scheint allein unter allen
Handels-Voͤlkern den Mythos der Fluͤgel am Helme und an den
Knoͤcheln des Merkur richtig aufgefaßt zu haben. Alles ist bei ihm auf
Zeitgewinn berechnet. Vielleicht haben wenige Guͤterbesizer auf dem
festen Lande bei Erbauung einer Kirche fuͤr ihre Unterthanen, bei
Anlegung eines Wirthshauses etc. auf Zeitgewinn fuͤr die Gehenden und
Kommenden gedacht. Am allerwenigsten scheint in manchen Laͤndern bei
Anlage der Landgerichte, Rentaͤmtern etc. auf Ersparung der Zeit
fuͤr den Landmann Ruͤksicht genommen zu seyn, und man darf wohl
sagen, daß, was der Bauer an Zeit verliert, die Beamten an Diaͤten
gewinnen. A. d. U..
Aus dem Mechanics' Magazine N. 291. S.
61.
Mit Abbildung auf Tab.
VII.
Ueber die Stellung der Kirchen, Wirthshäuser etc.
Es handelt sich hier darum, den Mittelpunkt der mittleren Abstaͤnde der
Haͤuser von dem Punkte, auf welchen die Kirche oder das Wirthshaus errichtet
werden soll, zu finden.
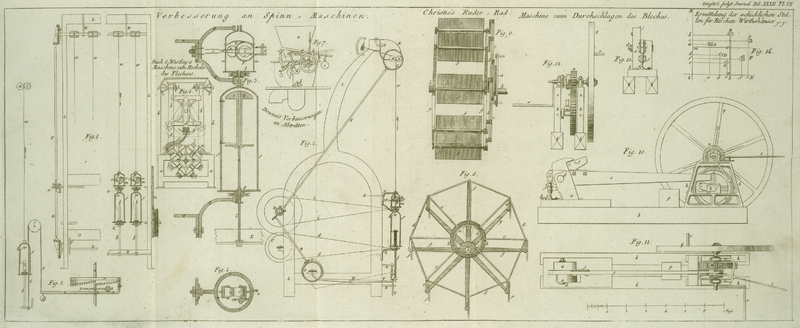
Die verschiedenen Haͤuser-Gruppen seyen in Fig. 14. A, B, C, D, E, F, in beliebigem Maßstabe auf einem
Grundrisse hingezeichnet. Man zeichne die beiden Geraden IM, IN, so daß
sie bei I sich unter einem rechten Winkel
durchschneiden, und ihre Durchschnittspunkte sowohl, als sie selbst, außer den
verschiedenen Gruppen zu liegen kommen. Aus den respektiven Mittelpunkten dieser
Gruppen laͤßt man senkrechte, Aa, Bb, Cc, Dd, Ee, Ff, auf die Linie IN, fallen, und zieht andere Senkrechte, A'a, B'b,
C'c, D'd, E'e, F'f, auf die andere Linie IM, und mißt die Laͤngen derselben auf dem allgemeinen Maßstabe des
Planes ab.
Man nimmt hierauf die Summe der Produkte aus der Zahl der Einwohner in jeder dieser
Hausergruppen und der Entfernung des Mittelpunktes einer jeden dieser
Haͤusergruppen von der Linie IN, und theilt
diese Summe der Produkte durch die Zahl der Einwohner in allen diesen
Haͤusergruppen oder Weilern: der Quotient gibt die Entfernung des gesuchten
Punktes, oder den Mittelpunkt der mittleren Entfernungen von der Linie IN.
Auf dieselbe Weise verfaͤhrt man, um die Entfernung dieses Punktes von der
Linie IM zu finden.
Wenn also, im gegebenen Falle, A, B, C, D, etc. die Zahl
der Einwohner in den verschiedenen Haͤusergruppen bezeichnet, so ist (A. Aa + B. Bb + C. Cc. + D. Dd. + E. Ee + F. Ff) ÷ (A + B + C + D + E + F)= IM Ferner A. A'a + B. B'b + C. C'c + D. D'd + E. E'e + F. F'f.) ÷ (A + B + C + D + E + F) = IN.
Man trage nun Im auf IM, In auf IN nach den erhaltenen
numerischen Resultaten auf, und zeichne mG
parallel mit IN, und nG, parallel mit IN. Der Durchschnitts-Punkt G ist der verlangte Punkt, auf welchem die Kirche oder das Wirthshaus
erbaut werden muß.
Tafeln