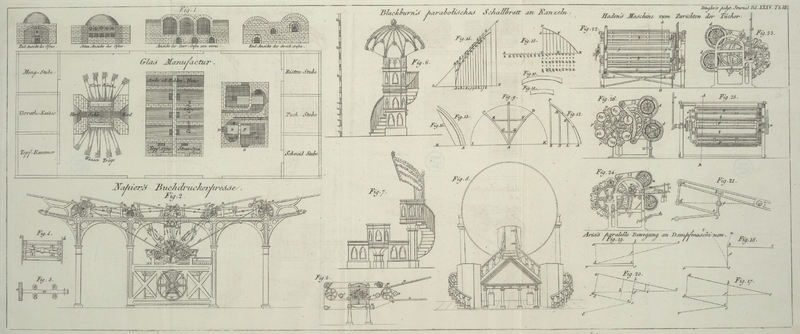
| Titel: | Ueber die parallele Bewegung an einer Dampfmaschine. Von J. R. Aris. |
| Fundstelle: | Band 35, Jahrgang 1830, Nr. LXIII., S. 263 |
| Download: | XML |
LXIII.
Ueber die parallele Bewegung an einer
Dampfmaschine. Von J. R.
Aris.
Aus dem London Journal of Arts N. 18 S.
281.
Mit Abbildungen auf Tab.
VII.
Aris, uͤber die parallele Bewegung an einer
Dampfmaschine.
Da ich in mehreren Abhandlungen uͤber die Dampfmaschine den Grundsaz, nach
welchem die parallele Bewegung eines Theiles derselben dem anderen mitgetheilt wird,
nicht erklaͤrt fand; so wird vielleicht folgende Erklaͤrung einigen
Lesern nicht unangenehm seyn.
Die gewoͤhnliche Methode, nach welcher der obere Theil der
Staͤmpelstange einer Dampfmaschine auf und nieder bewegt wird,
waͤhrend das Ende des Balkens sich in einem Kreisbogen bewegt, ergibt sich
aus Fig. 17.,
wo c den Mittelpunkt des Balkens bezeichnet, und a das Ende desselben, adbe und de ist eine Verbindung von
Hebeln, die an dem Balken angebracht ist, und welche Hebel durch die Mittelpunkte
a, d, b und e verbunden sind, so
daß sie das Parallelogramm adbe bilden, in welchem
ad = be, und
der Hebel de
=
den Theilen des Balkens ab oder bc. rs ist ein
anderer Hebel, der an einem Ende mit e verbunden ist (an
einem Winkel des Parallelogrammes), und mit dem anderen Ende an dem befestigten
Mittelpunkte r, und dessen Laͤnge gleich ist ab und bc, so
daß, wenn der Balken sich in horizontaler Lage befindet, der Mittelpunkt r mit dem Punkte d
zusammentrifft. Die Hebel ad und be beduͤrfen keiner bestimmten
Laͤnge: je laͤnger sie sind, desto genauer wird die parallele
Bewegung.
Da nun der Punkt b, Fig. 18., des Balkens von
dem feststehenden Mittelpunkte c aufsteigt, und der
Hebel rs von dem feststehenden Mittelpunkte r; da rs
=
bc; so wird der Punkt b (welcher sich in dem Kreisbogen, bu,
bewegt) beinahe eben so viel rechts hin abweichen, als s
(welches sich in dem Kreisbogen, st, bewegt)
links; folglich wird der Punkt, f, an welchem das obere
Ende der Staͤmpelstange befestigt ist, und welcher sich mitten zwischen b und s befindet, nach
keiner Seite hin abweichen, und sich in senkrechter Richtung auf und nieder bewegen.
Man ziehe aus dem Mittelpunkte des Balkens, c, Fig. 17., eine
Linie durch den Punkt l, und sie wird,
verlaͤngert, durch den Punkt, d, laufen, und
jeder Punkt in dieser Linie, der mit dem Parallelogramme a,
b, c, d, verbunden ist, wird sich auf eine aͤhnliche Weise, wie f, verhalten; folglich wird auch der Punkt, d, (an welchem der obere Theil der großen
Staͤmpelstange gewoͤhnlich angebracht ist) sich in senkrechter
Richtung auf und nieder bewegen, und die Bewegung wird doppelt so groß seyn, als
jene von f, da die Entfernung von dem Mittelpunkte des
Balkens das Doppelle betraͤgt.
Die Mittheilung der Bewegung fuͤr den Punkt d, wie
fuͤr den Punkt f, geschieht nach dem Grundsaze
des Storchschnabels, (Pantographes, „[der hier Pentagraph
heißt]“) mit welchem man Landkarten nach demselben, oder nach
vergroͤßertem oder verjuͤngtem, Maßstabe copirt. Man sieht dieß, wenn
man den Hebel rs von seinem feststehenden
Mittelpunkte r los macht. Er fuͤhrt jeden Punkt
der Linie cd, welche mit dem Parallelogramme abed verbunden ist, in senkrechter Richtung. Wenn
man den Punkt f eine Ellipse beschreiben laͤßt,
so wird der Punkt, d, und jeder andere Punkt in der
Linie cd, gleichfalls eine Ellipse beschreiben,
deren Groͤße aber im Verhaͤltnisse zur Entfernung vom Mittelpunkte des
Balkens c verschieden seyn wird. Wenn daher eine
parallele Bewegung zwischen den Punkten f und d Statt haben soll, so muß sie irgendwo auf der Linie
cd, wie bei g, h,
Fig. 20.,
oder zwischen den Punkten c und f außerdem Parallelogramm, wie bei i,
geschehen.
Da es nun besser ist, wenn der Punkt r des Hebels rs so weit von dem Punkte d entfernt liegt, daß er dem Ende des Balkens aus dem Wege kommt, so wird, wenn
die Lage des lezteren gegeben ist, es leicht seyn, die Laͤnge von rs (s. Fig. 19.) auf folgende
Weise zu bestimmen.
Man finde den horizontalen Abstand zwischen r und s, theile diesen in zwei gleiche Theile, und trage ihn,
von c aus, auf. Er wird auf b fallen, und bc wird gleich rs, nicht aber ab, wie in der vorigen Figur. Wenn nun die Eke d des Parallelogrammes sich parallel bewegen soll, ziehe man die Linie,
dc, und sie wird die Linie be in f
durchschneiden, naͤher gen e als gegen b fallen; man verlaͤngere die Linie b gegen s, und zeichne fs
=
fb. Man bringe dann das Ende s des Hebels rs auf
den Punkt s, und stelle das andere Ende dieses Hebels
so, daß rs vollkommen horizontal ist; so werden,
wenn der Balken in dieser Lage ist, die Punkte f und b sich in senkrechter Richtung bewegen. Wenn aber das
Ende s des Hebels rs
mit der Eke, e, des Parallelogrammes verbunden werden
muß; dann ziehe man eine Linie von dem Mittelpunkte c,
Fig. 20.,
durch den Punkt f, und sie wird den Hebel ad
in g durchschneiden, etwas uͤber d, wo die Staͤmpelstange eingehaͤngt
werden muß, wenn sie sich in senkrechter Linie bewegen soll.
Die Anwendung der hier beschriebenen parallelen Bewegung sieht man in Fig. 21., wo das Ende des
Balkens abc gehoben ist: die punktirte Linie zeigt
seine horizontale Lage.
Tafeln