| Titel: | Allgemeine Betrachtungen über Dampfmaschinen mit umdrehender Bewegung. Von T. Bakewell. |
| Fundstelle: | Band 35, Jahrgang 1830, Nr. XCIX., S. 416 |
| Download: | XML |
XCIX.
Allgemeine Betrachtungen uͤber
Dampfmaschinen mit umdrehender Bewegung. Von T. Bakewell.
Aus dem Journal of the Franklin Institution.
Maͤrz 1829. S. 179. im Bulletin d. Scienc. technol. N. 8. S.
348.
Mit einer Abbildung auf Tab. IX.
Bakewell, allgemeine Betrachtungen uͤber Dampfmaschinen mit
umdrehender Bewegung.
Die Versuche, welche man bisher gemacht hat, um die Leistungen einer Dampfmaschine
mit umdrehender Bewegung mit jenen einer Dampfmaschine mit abwechselnder Bewegung zu
vergleichen, gaben so wenig Uebereinstimmung in ihren Resultaten, daß wir glauben
unseren Lesern hieruͤber folgende Beobachtungen mittheilen zu
muͤssen.
Es ist als Naturgesez erwiesen, daß die Intensitaͤt einer groͤßeren
Kraft durch die Geschwindigkeit einer kleineren Kraft ersezt werden kann; daß, z.B.,
eine Kraft von zwei Pfund, die Einen Fuß durchlaͤuft, eine mechanische
Leistung hervorbringt, die einer Kraft von Einem Pfund gleich ist, welche zwei Fuß
durchlaͤuft. Mit anderen Worten folgt aus diesem Geseze, daß die mechanische
Leistung irgend einer Kraft sich wie der in einer gegebenen Zeit durchlaufene oder
beschriebene Raum verhaͤlt, dieser Raum mag durch eine gerade oder durch eine
krumme Linie ausgedruͤkt werden.
Wenn man ein Gewicht von zwei Pfund an jedem Ende eines Wagebalkens oder eines Hebels
erster Art in gleicher Entfernung von dem Stuͤzpunkte aufhaͤngt; so
wird dieser Hebel im Gleichgewichte seyn, und der Druk auf den Stuͤzpunkt ist
gleich einem Druke der beiden vereinigten Gewichte, d.h., einem Druke von vier
Pfund.
Wenn man an die Stelle des einen dieser beiden Gewichte von zwei Pfund ein Gewicht
von Einem Pfunde, aber in doppelter Entfernung vom Stuͤzpunkte,
haͤngt, wird der Hebel auch noch im Gleichgewichte bleiben; der Druk auf den
Stuͤzpunkt wird aber nur drei Pfund seyn.
Kein Raͤsonnement à priori kann
erklaͤren, warum hier ein Gewicht von zwei Pfund auf der einen Seite des
Stuͤzpunktes durch ein Gewicht voll Einem Pfund auf der anderen Seite des
Stuͤzpunktes, aber in einer groͤßeren Entfernung angebracht, im
Gleichgewichte seyn kann. Es ist nur ein Gewicht von Einem Pfunde, welches, von oben nach
abwaͤrts, auf den Stuͤzpunkt den Druk von Einem Pfunde
hervorbringt.Hieruͤber ließe sich manches sagen. Vergl. Archimed I. B. 1. S.
Ein Pfund kann also nur in Hinsicht auf Bewegung zwei
Pfunden gleich seyn, und es geschieht nur durch den groͤßeren Raum, welchen
es durchlaͤuft, daß es mit dem Gewichte von zwei Pfund im Gleichgewichte seyn
kann, nach dem oben angefuͤhrten Geseze.
Man muß also annehmen, daß die Bewegung nur durch den Ueberschuß des Gewichtes von
zwei Pfund uͤber das Gewicht von Einem Pfund hervorgebracht werden kann; daß
aber zugleich durch dieselbe Bewegung eine Ersaz-Eigenschaft (compensating propriety
propriété compensatrice) hervorgerufen wird, und daß folglich
die beiden ungleichen Gewichte im Gleichgewichte sind, und in Ruhe bleiben.
Dieser Lehrsaz wird wahrscheinlich klaͤrer und bestimmter werden, wenn wir
sagen, daß die erzeugte Bewegung und der durch dieselbe entstehende Ersaz
gleichzeitig sind, so wie es in anderen Faͤllen die ersezenden Eigenschaften
der Wirkung und Gegenwirkung sind.
Es ist schwer zu denken, daß die Ursache (action) nicht
vor der Wirkung (reaction) vorhanden ist, und doch ist
dieß der Fall. Und dieser Fall ist dem Falle des Hebels, der zwei ungleiche Gewichte
traͤgt, vollkommen analog.
Was das Verhaͤltniß betrifft, in welchem die Geschwindigkeit die Kraft ersezt,
so wird man, obschon man sieht, daß eine doppelte Geschwindigkeit einer Kraft eine
doppelte Wirkung hervorbringt, den Grundsaͤzen der Wissenschaft keine Gewalt
anthun, wenn man ein anderes Verhaͤltniß annimmt; es ist keine mathematische
Nothwendigkeit vorhanden, warum dieses Gesez vielmehr dieses Verhaͤltniß als
ein anderes fordern sollte.
Unter mathematischer Nothwendigkeit verstehe ich eine Nothwendigkeit derjenigen Art,
nach welcher der Durchmesser eines Kreises immer in demselben Verhaͤltnisse
zu seinem Umfange steht, obschon es uns durchaus unmoͤglich ist, dieses
Verhaͤltniß anders, als durch Linien auszudruͤken.
Theoretiker und Praktiker haben uͤber die Maschine mit umdrehender Bewegung
und uͤber die Kurbelbewegung mehr Widerspruͤche aufgestellt, als
uͤber irgend einen anderen Gegenstand. So schaukeln auch diejenigen, die an
ein Perpetuum mobile glauben, sich mit der Hoffnung, Kraft zu gewinnen, wenn sie dieselbe auf eine besondere
Weise, mittelst eines besonderen Mechanismus anwenden, waͤhrend sie doch
behaupten, daß Verlust an Kraft State hat (abgesehen von aller Reibung), wenn
eine geradlinige abwechselnde Bewegung in eine umdrehende verwandelt wird. Folgende
Bemerkungen uͤber Bewegung scheinen uns manche Irrthuͤmer und
Streitigkeiten beseitigen zu koͤnnen, wenn man die Folgen aus denselben eben
so frei zugibt, als man die Wahrheit derselben allgemein anerkennt.
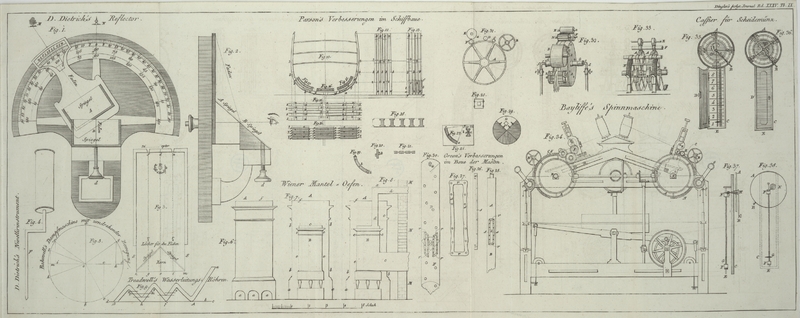
Fig. 5. stellt
einen Kreis vor, der das Innere eines kreisfoͤrmigen Ringes darstellt, in
welchem der Staͤmpel einer Maschine mit umdrehender Bewegung sich bewegt. Die
Linie ab stellt einen Cylinder dar, dessen
Staͤmpel gleiche Oberflaͤche mit dem vorigen hat, und dessen Lauf
gleich ist dem inneren Durchmesser des kreisfoͤrmigen Ringes.
Waͤhrend der Zeit also, als der Staͤmpel in der Maschine mit
umdrehender Bewegung einen vollkommenen Umlauf in dem Kreise von a bis a gemacht hat, wird
der Staͤmpel des Cylinders von a bis b herabgestiegen seyn, und wieder von b bis a hinauf.
Die von den beiden Staͤmpeln durchlaufenen Raͤume werden sich also
verhalten wie der Umfang des Kreises zu dem doppelten Durchmesser desselben, und
folglich wird die mechanische Leitung, so wie der Dampfverbrauch, in beiden
Maschinen sich verhalten, wie 3,142 zu 2.
Man mag was immer fuͤr eine Rechnungsmethode mit allen Kuͤnsten der
Arithmetik und der Algebra anwenden, man wird nie ein anderes Resultat erhalten. Es
wird nicht uͤberfluͤssig seyn hier zu bemerken, daß der Mittelpunkt
des Schlages des Staͤmpels in der Maschine mit umdrehender Bewegung, oder der
Punkt dieses Staͤmpels, an dessen beiden Seiten der Dampf gleiche Leistung
hervorbringt, nicht in der Mitte der Laͤnge des Staͤmpels liegt,
sondern in einem weiter vom Mittelpunkte entlegenen Punkte, wo der Umfang, welchen
dieser Punkt beschreiben wuͤrde, den großen Kreis in zwei Theile theilen
wuͤrde, deren Oberflaͤchen vollkommen aͤquivalent sind.
Wenn dieß nicht der Fall waͤre, so waͤren die hervorgebrachten
Leistungen nicht, wie wir annahmen, im Verhaͤltnisse der angewendeten
Dampfmenge.
Hr. Hammer ist im Franklin
Journal, December 1829, in einen gewoͤhnlichen Fehler gefallen,
indem er annimmt, daß wenn die gekruͤmmte Achse der Maschine mit
abwechselnder Bewegung einen Winkel von 45° mit der angewendeten Kraft
bildet, der mechanische Vortheil oder der Hebelarm nur die Haͤlfte des Maximums der Leistung ist, die dann Statt hat, wann die
gekruͤmmte Achse einen rechten Winkel bildet.
Die wahre Laͤnge eines Hebelarmes wird immer durch die auf die Richtung der
Kraft senkrechte Linie gemessen, die von dem Stuͤzpunkte bis zum
Durchschnittspunkte mit dieser Richtung gezogen wird. Wenn also die gekruͤmmte Achse
einem Winkel von 30° mit der Richtung der Kraft bildet, wie z.B. in e, so ist die mechanische Leistung die Haͤlfte
des Maximums, da co = der Haͤlfte von do. Wenn man dasselbe Raͤsonnement auf die
ganze Laͤnge des Viertelkreises db
anwendet, die von der gekruͤmmten Achse durchlaufen wird, waͤhrend der
Staͤmpel von o bis b
niedersteigt, so wird man eine geringere Leistung an der Maschine mit abwechselnder
Bewegung im Vergleiche mit jener mit umdrehender Bewegung wahrnehmen. Die beiden
Leistungen werden sich verhalten, wie der halbe Durchmesser ab zum Bogen db,
oder, wie wir oben sagten, wie 2 : 3,142. Aus obigen Bemerkungen, wenn sie
gegruͤndet sind, folgt, daß nach der Theorie die Maschine mit umdrehender
Bewegung keinen Ueberschuß oder keine Vermehrung der Kraft vor der anderen voraus
hat, und man weiß; daß sie in der Praxis unendliche Schwierigkeiten darbietet. Die
geringere Leistung der Maschine mit abwechselnder Bewegung wird durch eben so viel
Ersparung im Verbrauche des Dampfes ersezt, so daß, um dieselbe Kraft zu erzeugen,
nur der Cylinder um so viel vergroͤßert werden darf, daß der Hohlraum
desselben die Haͤlfte des Hohlraumes des Cylinders der Maschine mit
umdrehender Bewegung betraͤgt. Der behauptete Verlust an Kraft bei der
Maschine mit abwechselnder Bewegung ist nur eine Unachtsamkeit, die bloß bemerkt zu
werden verdient, um ihr alle Gerechtigkeit widerfahren zu lassen.
Die beste Maschine mit umdrehender Bewegung, die ich gesehen habe, ist jene, die Hr.
Rutter zu Cincinnati erbaute, und die auf einem
kleinen Dampfbothe allgewendet wird. Der Grundsaz der Ausdehnung des Dampfes wurde
bei derselben in eben dem Grade angewendet, wie bei den Maschinen mit abwechselnder
Bewegung und mit hohem Druke. Die Schwierigkeit, die sich hier zeigte, die
Entweichung des Dampfes zu verhindern, und die Maschine gehoͤrig arbeiten zu
lassen, veranlaßten den Austausch derselben mit einer gewoͤhnlichen Maschine,
an welcher der Grundsaz der Expansion in demselben Grade angewendet wurde, ohne daß
man deßwegen den Kessel zu aͤndern noͤthig hatte. Die Folge hiervon
war, daß, bei gleichem Kohlenverbrauche, das Dampfboth jezt 8 engl. Meilen in Einer
Stunde lief, waͤhrend es ehevor mit der Maschine mit umdrehender Bewegung nur
7 1/2 engl. Meilen zuruͤklegte.
Man hat oft behauptet, daß, wenn man eine Maschine mit zwei Cylindern und zwei
gekruͤmmten unter einem rechten Winkel verbundenen Achsen anwendet, dieselbe
Kraft auf die gemeinschaftliche Achse bei jedem Punkte der Umdrehung wirkt. Ein Blik
auf Figur 5.
wird die Unrichtigkeit dieser Behauptung zeigen.
Es seyen a und d die beiden
unter einem rechten Winkel gekruͤmmten Achsen; a, in der Richtung der
Kraft gelegen, wird keine Wirkung aͤußern; d, als
senkrecht auf die Wirkung der Kraft, wird das Maximum
seiner Leistung durch die groͤßte Laͤnge des Hebels do ausgedruͤkt haben. Wir wollen diese
Leistung = 100 ersezen.
Wir wollen nun sezen die beiden gekruͤmmten Achsen befinden sich in den
respectiven Lagen f und g: g
gehe von oben nach abwaͤrts, und f von unten nach
aufwaͤrts; jede derselben wird durch eine Kraft bewegt werden, welche durch
die Linien oi und ok ausgedruͤkt wird, oder die sich zu der, welche vorher auf den
Hebelarm od wirkte, wie 70 : 100 verhaͤlt.
Die beiden Kraͤfte, die auf die zwei Hebelarme, f
und g, wirken, werden also jede gleich 70, und beide
zusammen 140 seyn, und mit dieser vereinten Kraft die Achse drehen.
Wenn, um die zu große Leistung, welche in diesem Falle Statt hat, zu vermindern, man
die beiden gekruͤmmten Achsen einander naͤherte, so daß sie einen
kleineren Winkel, als einen rechten, bildeten, so wuͤrden dann Faͤlle
eintreten, wo die Leistung 140 um Vieles uͤbertroffen wuͤrde. Dieß
geschaͤhe z.B. in der Lage l und h, wo die Gewalt, mit welcher die beiden Kraͤfte,
die auf die Hebelarme l und h angebracht sind, wirken, jede durch die Linie om ausgedrukt ist, die wir gleich 80 sezen, was
eine Gesammtleistung von 160 geben wuͤrde. So waͤren demnach die
aͤußersten Unterschiede, welche die nach und nach auf die gekuͤmmten
Achsen angebrachten Kraͤfte hervorbringen koͤnnen, im
Verhaͤltnisse wie 140: 100, oder, unter der angenommenen Voraussezung, 40; in
allen uͤbrigen Faͤllen, wo diese Achsen einen anderen, als einen
rechten Winkel bilden, wuͤrden sie noch groͤßer seyn.
Tafeln