| Titel: | Methode, die Eintheilung auf Schnellwagen, deren man sich bedient, um die Feinheit oder die Nummern der Baumwollengespinnste zu bestimmen, mit der größten Genauigkeit zu ziehen. Von Hrn. A. Schlumberger. |
| Fundstelle: | Band 36, Jahrgang 1830, Nr. II., S. 5 |
| Download: | XML |
II.
Methode, die Eintheilung auf Schnellwagen, deren
man sich bedient, um die Feinheit oder die Nummern der Baumwollengespinnste zu
bestimmen, mit der groͤßten Genauigkeit zu ziehen. Von Hrn. A. Schlumberger.
Aus dem Bulettin de la Société industr. de
Mulhausen. Nro. 11. S. 46.
Mit Abbildungen auf Tab.
I.
Schlumberger, uͤber Eintheilung auf Schnellwagen
etc.
Nach einer k. Ordonnanz vom J. 1819 soll das metrische System allein in Frankreich
zur Nummerirung des Baumwollengarnes angewendet werden.
Eine Straͤhne von 1000 Meter Laͤnge und 500 Gramm (1 Pfd.) Schwere ist
von N. 1. Wenn, bei derselben Laͤnge, das Gewicht nur 250 Gramm
betraͤgt, ist der Faden von N. 2. Bei 125 Gramm von N. 4. u.s.f. Die Nummer
verhaͤlt sich also immer umgekehrt, wie das Gewicht.
Das Waͤgen der Straͤhne ist, zumal bei feinen Nummern, eine zu delicate
Sache, als daß man es mit gewoͤhnlichen Wagen auf eine verlaͤssige
Weise unternehmen koͤnnte. Ueberdieß muͤßte man jedes Mal noch
rechnen, um das Gewicht in Nummern zu verwandeln. Um diesen Nachtheil zu beseitigen,
hat man ein Instrument erfunden, welches auf eine directe Weise die Nummer des
Garnes anzeigt, und zwar mittelst eines beweglichen Zeigers auf einem in Grade
getheilten Kreisbogen. Dieses Instrument ist eine Schnellwage (roͤmische
Wage, romaine), derjenigen aͤhnlich, welche ich
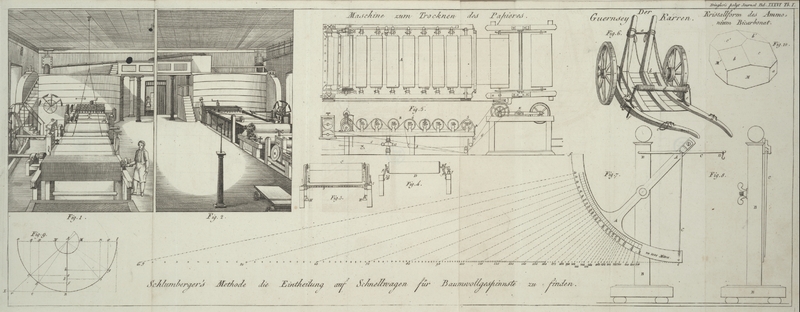
hier der Gesellschaft zu unterlegen die Ehre habe. (Fig. 7. 8.) Ein Viertelkreis aus
Messing, A, auf einem hoͤlzernen Traͤger
B befestigt, ein kleiner Hebel C in Form eines T, der auf
einer Achse im Mittelpunkte des Viertelkreises beweglich ist, und ein kleiner Haken
D an einem der oberen Arme des Hebels ist Alles,
woraus dieses Instrument besteht.
Der untere Arm des Hebels dient als Zeiger. Man bezeichnet gewoͤhnlich die
Durchschnittslinie des Umfanges des Viertelkreises und der senkrechten durch die
Aufhaͤngungsachse durchlaufenden Flaͤche mit einem Pfeile. Die Spize
des Zeigers muß sich auf diesem Pfeile befinden, wenn kein Gewicht an dem Haken
aufgehaͤngt ist. Man begreift hiernach, daß die Neigung des Zeigers sich
vermindern muß, je mehr man Gewicht an dem Haken anhaͤngt, und daß man
folglich auf einem Kreisbogen die Neigung der Nadel anzeigen kann, die sie bei jedem
an dem Haken aufgehaͤngten Gewichte haben muß. Da nun jede Nummer mit einem
gewissen Gewichte correspondirt, so kann man jedes Mal direct die correspondirende Nummer, Statt
des Gewichtes, angeben.
Nach dem Dictionaire technologique scheint man die
Eintheilung des Maßstabes auf den gewoͤhnlich im Handel verkaͤuflichen
Wagen auf folgende Weise vorzunehmen.
Man faͤngt damit an, daß man an dem Haken ein gewisses Gewicht
aufhaͤngt, z.B., 20 Gramm. Nachdem das Gleichgewicht mit dem Zeiger
hergestellt wurde, bezeichnet man den Ort, wo die Nadel stehen blieb. An diesen Ort
kommt nun die Nummer 25., welche mit 20 Gramm correspondirt. Man haͤngt dann
ein anderes Gewicht an den Haken, z.B. 10 Gramm, und bemerkt nach hergestelltem
Gleichgewichte neuerdings die Stelle, wo die Spize stehen bleibt: dieß Mal wird die
Stelle N. 50. seyn, die mit 10 Gramm correspondirt. Auf
diese Weise faͤhrt man bis zur hoͤchsten Nummer fort, die man erhalten
will. Da es indessen schwer halten wuͤrde, sich sehr genaue Gewichte
fuͤr jede einzelne Nummer zu verschaffen, so begnuͤgt man sich,
nachdem man die Stellen fuͤr eine Reibe von Nummern erhalten hat, den Bogen,
der zwischen zwei bestimmte Punkte faͤllt, in so viel gleiche Theile zu
theilen, als Nummern oder halbe Nummern zwischen diese beiden Punkte fallen.
Allein, diese Methode ist nichts weniger als genau. Denn, wenn man auf einem
Viertelkreise die Stelle fuͤr N. 25. und die
Stelle fuͤr N. 50. mit aller Genauigkeit bestimmt
hat, und den Zwischenraum zwischen beiden in 25 gleiche Theile theilt, so ergibt
sich von N. 25. auf 26. dieselbe Entfernung, wie von N. 49. auf 50. Man weiß, daß die Nummern sich umgekehrt,
wie die Gewichte verhalten; folglich muß auch die Entfernung einer Nummer von der
anderen in demselben Verhaͤltnisse verschieden seyn, in welchem die
correspondirenden Gewichte von einander abweichen.
N.
25.
correspondirt
mit
20,000
Gramm.
N.
26.
–
–
19,231
–
––––––
Unterschied.
0,769
N.
49.
correspondirt
mit
10,204
Gramm.
N.
50.
–
–
10,000
–
––––––
Unterschied
0,204.
Wenn folglich x + 0,769 = der Entfernung zwischen N. 25
und 26., und x + 0,204 =
der Entfernung zwischen N. 49
und 50.,
so ist offenbar x + 0,769 großer
als x + 204, und die Entfernung zwischen 25 und 26 muß
groͤßer seyn, als die zwischen 49 und 50. Nach obiger Methode sind aber diese
Entfernungen gleich; folglich ist weder N. 26 noch N. 49 genau.
Um den Maßstab an der Schnellwage, die hier vor Augen liegt, einzutheilen, habe ich
mich einer anderen Methode bedient, die auf einer wohlbekannten Eigenschaft der
Hebel beruht. Man weiß, daß, wenn Gleichgewicht Statt haben soll, zwei an einem
Hebel angebrachte Kraͤfte sich umgekehrt verhalten muͤssen, wie die
Senkrechten, die man von dem Stuͤzpunkte auf ihre Richtung herablaͤßt.
Man denke sich in Fig. 7, einen Viertelkreis, ef, von der Spize
des Zeigers von e auf der senkrechten Flaͤche,
die durch die Aufhaͤngungsachse laͤuft, beschrieben. Wenn man nun auf
den Punkt e eine Tangente eg
dieses Kreises zieht, so wird, so bald die Laͤnge dieser Tangente fuͤr
eine einzige Nummer bestimmt ist, oder fuͤr ein einziges auf dem Haken
haͤngendes Gewicht, zugleich die Laͤnge derselben fuͤr jede
andere Nummer oder fuͤr jedes andere Gewicht bestimmt seyn.
Wenn man die Schnellwage betrachtet, so wird man bei dem ersten Blike wahrnehmen, daß
einer der Haupttheile derselben, der als Zeiger dient, nichts anderes als ein Hebel
mit gekruͤmmten Armen ist, auf welchen zwei Kraͤfte durch ihr Gewicht,
folglich senkrecht wirken. Wenn also Gleichgewicht seyn soll, so muͤssen die
Gewichte sich umgekehrt verhalten, wie ihre Entfernungen von der senkrechten
Flaͤche durch die Aufhaͤngungsachse. Da nun die Schwere des Zeigers
sich nicht aͤndert, und das Gewicht, welches am Haken haͤngt, allein
wandelbar ist; da ferner die Tangente senkrecht auf die verticale Flaͤche
steht; so kann man auf dieser Linie die Entfernung des Zeigers von der senkrechten
Flaͤche andeuten. Die, durch eine gewisse Laͤnge ausgedruͤkte,
Entfernung wird sich immer gerade wie die aufgehaͤngten Gewichte
verhalten.
Dieß vorausgesezt, handelt es sich nun darum, eine genaue Tabelle zu verfertigen,
welche
1) die verlangten Nummern,
2) die denselben correspondirenden Gewichte,
3) die Laͤnge, welche die Tangente bei jedem Gewichte hat, mit
Verlaͤssigkeit angibt.
Ich fuͤge diese Tabelle, deren ich mich zur Eintheilung der vorliegenden
Schnellwage bediente, hier bei. Da sie vorzuͤglich zur Bestimmung feiner
Gespinnste dienen soll, faͤngt sie nur bei N. 45. an. Von 40 bis 151. ist
jede zweite Nummer angegeben; hierauf jede dritte; dann jede fuͤnfte; u.s.f.
bis 500.
Fuͤr N. 40. nahm ich 1,5 Meter als Laͤnge der Tangente.
Da nun 12,5 Gramm mit N. 40. correspondiren, so beschwerte ich den Zeiger so, daß er
damit im Gleichgewichte stand, wann er mit seiner Spize N. 40. zeigte. Es ist
einerlei, welche Nummer man waͤhlt, wann nur der Zeiger mit dem
correspondirenden Gewichte genau ins Gleichgewicht gesezt wird. Wenn man gleich Anfangs
dafuͤr sorgte, den Zeiger schwerer zu lassen, als er seyn soll, so wird es
sehr leicht, ihm die noͤthige Schwere auf das Genaueste zu ertheilen, indem
man mit einer feinen Feile so wenig von demselben wegnehmen kann, als man will.
Die Schnellwage besezt eine Genauigkeit, die meine Erwartung weit uͤbertraf.
Ich fuͤrchtete, daß die Reibung der Achse auf der Unterlage bedeutende
Abweichungen bei hohen Nummern erzeugen koͤnnte; da man aber den Hebel sehr
leicht machen kann, so kann man die Reibung hier beinahe als 0 betrachten, wenn
anders die Achse und ihre Unterlagen mit Sorgfalt gebaut sind.
Tabelle.
Nummer.
Gewicht einer
Straͤhne.
Laͤnge
der Tangente.
Nummer.
Gewicht einer
Straͤhne.
Laͤnge
der Tangente.
40
12500
150000
76
6579
78947
41
12195
146341
77
6493
77922
42
11905
142857
78
6410
76923
43
11628
139534
79
6329
75937
44
11364
136363
80
6250
75000
45
11111
135333
81
6173
74074
46
10869
130434
82
6097
73170
47
10638
127659
83
6024
72289
48
10417
125000
84
5952
71428
49
10204
122448
85
5882
70588
50
10000
120000
86
5814
69767
51
9804
117647
87
5747
68965
52
9615
115382
88
5682
68181
53
9434
113207
89
5618
67415
54
9259
111111
90
5556
66666
55
9090
109090
91
5494
65934
56
8928
107142
92
5435
65217
57
8772
105262
93
5376
64516
58
8621
103448
94
5319
63829
59
8475
101693
95
5263
63157
60
8333
100000
96
5208
62500
61
8197
98360
97
5155
61855
62
8065
96774
98
5012
61224
63
7936
95238
99
5051
60606
64
7813
93750
100
5000
60000
65
7692
92307
101
4951
59403
66
7576
90909
102
4902
58823
67
7465
89552
103
4854
58252
68
7355
88235
104
4808
57692
69
7246
86956
105
4762
57142
70
7143
85714
106
4717
56605
71
7042
84507
107
4673
56074
72
6944
83333
108
4629
55555
73
6849
82191
109
4587
55045
74
6756
81081
110
4545
54545
75
6667
80000
111
4503
54054
Nummer.
Gewicht einer
Straͤhne.
Laͤnge
der Tangente.
Nummer.
Gewicht einer
Straͤhne.
Laͤnge
der Tangente.
112
4464
53571
163
3067
36800
113
4425
53097
166
3012
36144
114
4386
52631
169
2958
25526
115
4348
52173
172
2906
34883
116
4310
51724
177
2824
33393
117
4274
51282
182
2747
32967
118
4237
50847
187
2673
32085
119
4202
50420
192
2604
31250
120
4167
50000
197
2538
30456
121
4123
49586
202
2475
29702
122
4098
49180
207
2415
28985
123
4065
48780
212
2358
28301
124
4032
48387
217
2304
27649
125
4000
48000
222
2252
27027
127
3937
47244
232
2155
25862
129
3876
46511
242
2066
24793
131
3816
45801
252
1984
23769
133
3759
45112
262
1908
22900
135
3703
44444
272
1838
22059
137
3649
43795
282
1773
21276
139
3597
43165
292
1712
20549
141
3546
42553
302
1655
19867
143
3496
41958
312
1602
19230
145
3448
41379
322
1552
18633
148
3378
40540
332
1508
18072
151
3311
39735
350
1428
17143
154
3246
38961
400
1250
15000
157
3184
38216
450
1100
13333
160
3125
37500
500
1000
12000
Bericht des Hrn. Karl Naͤgely, im Namen des Ausschusses
fuͤr Mechanik, uͤber obige Abhandlung des Hrn. A.
Schlumberger.
Es war Hrn. Schlumberger aufbehalten, dieses allgemein
bekannte, aber noch immer fehlerhafte Instrument zu verbessern. Im Inneren
Frankreichs nennt man es Peson; so nennt es
wenigstens Poinsot in seiner Statique.
Der Dictionnaire technologique behauptet, daß dieses
Instrument, wegen der Reibung, zu dem Zweke, zu welchem es bestimmt ist, wenig
taugt, und daß es keine genauere Eintheilung verdient, indem seine Fehler es
gaͤnzlich aus dem Handel verbannen werden.
Wir koͤnnen mit dieser Ansicht nicht uͤbereinstimmen, indem
taͤgliche Erfahrung uns uͤberzeugt, daß man an einer mit Sorgfalt
gearbeiteten Schnellwage die Reibung als 0 betrachten kann. Wenn sie genau und nach
der wahren Methode eingetheilt ist, so gewahrt sie alle moͤgliche
Genauigkeit, und sie wird in Fabriken immer von großem Nuzen seyn. Es wird schwer halten, ein einfacheres,
wohlfeileres, und zu seinem Zweke brauchbareres Instrument zu erfinden.
Um eine Schnellwage gehoͤrig eintheilen, und die Genauigkeit der Operation
mathematisch erweisen zu koͤnnen, muͤssen wir zur Theorie des Hebels
zuruͤk. Wir wissen nach derselben, daß, wenn Gleichgewicht zwischen zwei an
den Enden eines Hebels angebrachten Kraͤften Statt haben soll, sie sich
umgekehrt wie die Senkrechten aus den Stuͤzpunkte auf ihre Richtung
verhalten.
Dieß vorausgesezt, koͤnnen wir die Schnellwage NAMB (Fig.
9.) als einen gekruͤmmten Hebel betrachten, der seinen
Stuͤzpunkt in A hat. Wenn die Arme AM und AN im
Gleichgewichte sind, so ist der Mittelpunkt der Schnellwage in senkrechter Lage. Die
Kraft welche der Wirkung widerstrebt, die diesen Punkt aus der Senkrechten zu
bringen trachtet, ist eine bestaͤndige Kraft, und es ist wesentlich, daß man
sich wohl uͤberzeugt, daß diese Kraft nie wechselt, der Arm mag was immer
fuͤr eine Lage haben.
Wir wollen zu groͤßerer Deutlichkeit die verschiedenen Linien, die diesen
Gegenstand erlaͤutern koͤnnen, mit punktirten Linien hier andeuten,
und mit kleinen Buchstaben bezeichnen.
Es ist offenbar, daß, wenn man in l nach und nach
Gewichte von verschiedener Schwere aufhaͤngt, die bestaͤndige Kraft
der Linie AB uͤberwunden werden, und nach
und nach die Lagen Ad, Ac etc. annehmen wird.
Nach den Grundsaͤzen der Trigonometrie wird nun
hg = Sinus des Winkels
hAg;
Ki = Sinus des Winkels
kAi;
fA = Cosinus des
Winkels dAf, des Complementes von hAg;
eA = Cosinus des
Winkels cAe, des Complementes von kAi;
und, da die Sinus der Winkel
gleich sind den Cosinus ihrer Complementen, hg = Af, Ki = eA.
Wir haben frei haͤngende Gewichte an den Armen des Hebels angenommen; woraus
folgt, daß die Richtung der Kraͤfte senkrecht ist, und folglich in verkehrtem
Verhaͤltnisse der Linien
As, Ap, An, Aq.
Oder auch weil
As = hg,
Ap = fs,
An = Ki
Aq = ec
wie die Linien hg, fd, Ki,
ec.
Wir haben aber gesehen, daß die Linie hg = Af, und ki = Ae ist; es folgt daher, daß die Kraͤfte
sich verhalten wie die Seiten der Dreieke Afd, Ace,
oder wie die Seiten der Dreieke ADt, ABr
, die den ersteren aͤhnlich sind.
Da nun die bestaͤndige Kraft, die den bei l
angehaͤngten Gewichten entgegensteht, und durch den Halbmesser AB ausgedruͤkt wird, immer dieselbe bleibt,
der Hebel mag in was immer fuͤr eine Lage kommen, so wird das Gewicht oder
die in l wirkende Kraft durch die Tangenten Bt, Br, etc. dargestellt seyn, welche genau im
Verhaͤltnisse des Gewichtes zunehmen.
Der Viertelkreis Ocdb der Schnellwage stellt den
Sector dar, welchen der Zeiger von der Verticalen AB bis zur Horizontalen Ao durchlaufen
kann; es ist also leicht auf den verschiedenen Punkten die Nummern anzudeuten,
welche mit den Gewichten correspondiren. Die Verlaͤngerung der Linien Ad, Ac wird die Tangente Bx in Theile theilen, deren Laͤnge mit
diesen Gewichten im Verhaͤltnisse steht. Dadurch kann man sich nun die
Eintheilung des Viertelkreises durch Anhaͤngung eigener Gewichte fuͤr
jede Nummer ersparen. Es ist genug, wenn die Laͤnge der Tangente fuͤr
irgend eine Nummer genau bestimmt ist, um die uͤbrigen Tangenten fuͤr
jede andere Nummer zu finden; man darf nur aus den Theilungspunkten r, t, etc. die Geraden rA,
tA nach dem Mittelpunkte der Bewegung A
fuͤhren; dort, wo diese Linien den Viertelkreis durchschneiden, werden sie
die correspondirende Nummer mit aller Genauigkeit angeben.
Dieses Verfahren bei der Eintheilung vertheuert das Instrument durchaus nicht, denn
eine solche aͤußerst genau gearbeitete Schnellwage kostet nicht mehr als 35
Franken.
Hr. Schlumberger verdient den Dank der Gesellschaft.
Tafeln