| Titel: | Ueber die sphärische Aberration einer Demantlinse. Von Hrn. Andr. Pritchard. Mitgetheilt von C. R. Goring, M. D. |
| Fundstelle: | Band 37, Jahrgang 1830, Nr. I., S. 1 |
| Download: | XML |
I.
Ueber die sphaͤrische Aberration einer
Demantlinse. Von Hrn. Andr.
Pritchard. Mitgetheilt von C. R. Goring, M.
D.
Aus dem Edinburgh Journal of Science. N. S. N. 4.
April. 1830. S. 317.
Mit einer Abbildung auf Tab. I.
Pritchard, uͤber die sphaͤrische Aberration einer
Demantlinse.
Da die ausgezeichnete Klarheit und Kraft der Demantlinsen als
Vergroͤßerungsglaͤser von dem Publikum noch nicht gehoͤrig
gewuͤrdigt zu seyn scheint, was ohne Zweifel von dem Mangel an einfacher
Vergleichung mit der sphaͤrischen Aberration am Glase und anderen
Koͤrpern von geringerer Brechungskraft gegen das Licht herruͤhrt, so
will ich hier auf eine einleuchtende und handgreifliche Weise die wirkliche
Longitudinal-Aberration an denselben darzustellen versuchen.Wir haben schon vor 3 Jahren (Polyt. Journ. B. XXV. S. 85.) von den trefflichen Demantlinsen des Hrn. Pritchard Notiz gegeben, zweifeln aber sehr, ob
im suͤdlichen Deutschland auch nur Eine vorhanden ist. Unsere Optiker
haben, so herrliche Mikroskope sie liefern, keinen Apparat zum
Demantschleifen, und unsere Naturhistoriker haben kein Geld, sie aus England
kommen zu lassen: denn heute zu Tage hat der schlechteste Komoͤdiant
mehr Gehalt als der beste Naturhistoriker; und uͤberdieß will man an
einigen Orten vielmehr, daß alles stokblind seyn, oder wenigstens werden
soll. Statt daß es klarer und Heller saͤhe.A. d. Ue.
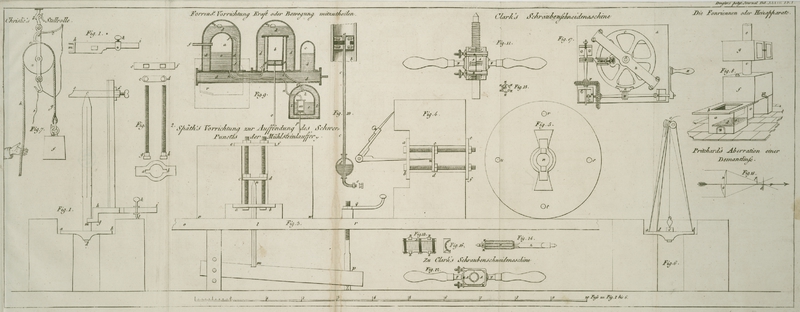
Fig. 18.
zeigt einen Durchschnitt zweier Halblinsen: beide sind convex-plan. Die
obere, D, ist Demant, und von gleich
vergroͤßernder Kraft und Halboͤffnung, wie die untere G, die aus Glas ist.Bei Zeichnung der Figur habe ich die Halbmesser wie 8 zu 3 angenommen, indem
es durch die sorgfaͤltigsten Versuche erwiesen ist, daß die
Kraͤfte einer Demantlinse und einer Linse aus Tafelglas von gleichem
Halbmesser sich verhalten, wie 8 zu 3. Diese Verhaͤltnisse werden,
nach den verschiedenen Refractiv-Indices der angewendeten Steine,
nothwendig etwas verschieden ausfallen muͤssen. Die Linsen in der
Figur sind, zur Correction der Dike, etwas schief, damit der Brennpunkt F in denselben Punkt faͤllt. A. d. O.
F ist der Hauptbrennpunkt an beiden Linsen fuͤr
die inneren Strahlen: d und g sind die Brennpunkte fuͤr die aͤußeren Strahlen derselben.
Es ist folglich der Raum Fd die
Longitudinal-Aberration der Demantlinse, und gF die der Glaslinse. Diese geometrische Darstellung wird, wie ich
erwarte, auch fuͤr die Augen eines solchen Lesers deutlich genug seyn, der in
der feineren Kunst zu sehen halb blind ist. Ich habe mich indessen noch des Werkes
des Hrn. Coddington bedienen wollen, um nach einer von ihm S.
93. seines Werkes gegebenen Formel die sphaͤrische Aberration zu berechnen.
Die Formel ist:
Textabbildung Bd. 37, S. 2
Wenn wir den Refractiv-Index des Demantes zu 2,5 (µ) als mittleren Durchschnitt annehmen (er steigt bis 2,755), so
wird obige Formel, in Zahlen ausgedruͤkt, folgende Gestalt erhalten:
Textabbildung Bd. 37, S. 2
also beinahe oder fast 3/7 seiner eigenen Dike, waͤhrend es allgemein bekannt ist, daß die Aberration
einer Glaslinse von derselben Form und in derselben Lage 7/6 ihrer eigenen Dike betraͤgt. Da aber die Dike einer
Demantlinse bedeutend geringer seyn wird, als die einer Glaslinse von derselben
Kraft und Oeffnung, so wird es noͤthig dieselben einzeln zu berechnen. Wenn
man die in der geometrischen Darstellung gegebenen Verhaͤltnisse annimmt,
wird man fuͤr den Demant 255, und fuͤr die Dike des Glases 758 finden.
Also 3/7 von 255 wird die Longitudinal-Aberration der Demantlinse seyn, d.h.,
108, und 7/6 von 758 die des Glases, d.h., 884; oder, in anderen Worten, der Demant
wird nur ungefaͤhr Ein Neuntel der wirklichen
Aberration einer Glaslinse von derselben Kraft und Oeffnung besizen.Man muß bemerken, daß, wenn man dem Demante seine groͤßte Wirkung
geben will, er in eine Meniscus-Linse
ausgeschliffen werden muß, so daß die Halbmesser seiner Oberflaͤchen
sich beinahe wie 2 zu 5 verhalten, wo dann die Aberration stark unter jene
einer plano-convexen Linse reducirt wuͤrde. Siehe Coddington S. 111. A. d. O. Es ist also einleuchtend, daß der Demant seine Vorzuͤge als
Vergroͤßerungsglas aus zwei Ursachen erhaͤlt: 1) ist seine
sphaͤrische Aberration, durch seine eigene Dike
ausgedruͤkt, bei weitem geringer, als die des Glases; 2) ist diese
Dike selbst auch weit geringer, als die einer Glaslinse von derselben Kraft und
Oeffnung, und diese beiden Groͤßen sind es, die vereint die wirkliche
Aberration ausdruͤken. Man darf ferner auch nicht vergessen, daß die
gewaltige Brechkraft des Demantes (welche die Ursache seiner schwachen
sphaͤrischen Aberration ist) hier zufaͤllig mit einer
Zerstreuungskraft verbunden ist, die gleichfalls geringer ist, als die des Glases;
denn staͤnde die Zerstreuungskraft im Demante im Verhaͤltnisse zur
Brechkraft, so wuͤrde dadurch so viele Farbe erzeugt worden seyn, daß der
Vortheil der schwachen sphaͤrischen Aberration desselben dadurch aufgewogen
wuͤrde. Es thut mir Leid, daß ich dem Publikum bisher noch keine vollkommene
flach-convexe Demantlinse mittheilen konnte, ich bin aber gegenwaͤrtig
auf dem Punkte, diesem Uebel abzuhelfen: der Stein, den ich in der Arbeit habe,
verspricht auf der flachen
Seite alle Vollkommenheit und zeigt weder Spruͤnge noch Polarisation.
Tafeln