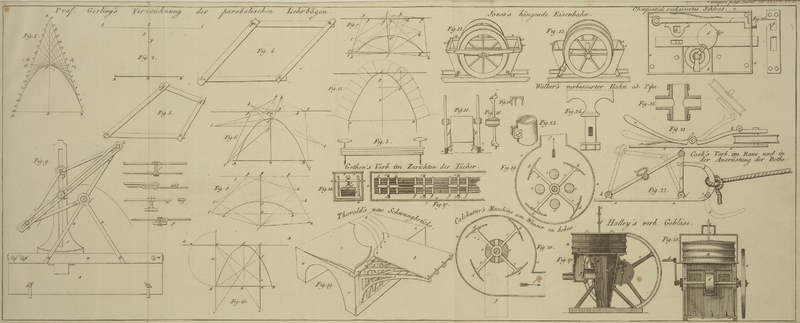
| Titel: | Verzeichnung parabolischer Lehrbögen, von Prof. Gerling in Marburg. |
| Autor: | Gerling |
| Fundstelle: | Band 38, Jahrgang 1830, Nr. XXIII., S. 81 |
| Download: | XML |
XXIII.
Verzeichnung parabolischer Lehrboͤgen, von
Prof. Gerling in
Marburg.
Mit Abbildungen auf Tab.
II.
Gerling, Verzeichnung parabolischer Lehrboͤgen.
Die Parabel als eine der einfachsten krummen Linien
scheint nicht nur in mehreren Faͤllen als Gewoͤlblinie wesentliche Dienste leisten zu koͤnnen (siehe
z.B. Eytelwein Statik §. 390.), sondern ist auch
fuͤr manche andere technische Constructionen, z.B. bei Lampenspiegeln (siehe
Abendroth Ritzebuͤttel und das Seebad zu
Cuxhaven S. 101 folgend) Reverberiroͤfen, Schelldekeln u.s.w. so
nuͤzlich, daß natuͤrlich die Frage entsteht: Woher es wohl komme, daß
sie verhaͤltnißmaͤßig so selten angewendet wird? – Die Antwort
auf diese Frage scheint mir darin zu liegen, daß leichte und bequeme Methoden die
Lehrboͤgen fuͤr dieselbe zu zeichnen nicht allgemein bekannt sind, und
habe ich wirklich bis jezt vergeblich nach solchen Anweisungen gesucht. –
Demnach glaube ich also etwas Nuͤzliches zu thun, wenn ich Vorschlage dazu
mittheile, welche (auf richtigen mathematischen Grundsaͤzen, deren
Auseinandersezung nicht weiter, hierher gehoͤrt, beruhend) als Anleitung
fuͤr die Arbeiter selbst dienen
koͤnnen.
–––––––––
Aus diesem rein praktischen Gesichtspunkt theile ich alle Parabeln in drei
Classen.
1) Parabeln von solcher Groͤße, daß sich die Lehrboͤgen nur auf dem
Zimmerplaz machen lassen; z.B. fuͤr Bruͤkenboͤgen u. dergl.
2) Parabeln von mittlerer Groͤße, deren Lehrboͤgen sich auf dem
Fußboden einer Werkstatt beschreiben lassen; z.B. fuͤr Oefen u. dergl.
3) Kleine Parabeln, die man auf dem Reißbrett verzeichnen oder doch auf dem Tisch
ausarbeiten kann; z.B. fuͤr Lampen u. dergl.
Erste Classe.
Hier braucht nur die untere Weite und die Hoͤhe des Gewoͤlbes gegeben
zu seyn. Die Weite sey (Fig. 1.) als Grundlinie
mit AB bezeichnet und in A und B z.B. Pfloͤke in den Boden
getrieben und Loͤcher eingebohrt. Auf der Mitte von AB in D errichte man
das Perpendikel DE (die Richtung der Axe) doppelt so lang als die Hoͤhe (bis zum Scheitel
S) vorgeschrieben ist, nach E und bezeichne E (welches man dadurch erst
pruͤft, daß man AE und EB nachmißt, welche gleich lang seyn
muͤssen). Nun theile man durch fortgeseztes Halbiren, z.B. mit der Schnur, die Linien AE und BE in 8,
16, 32 u.s.w. gleiche Theile (in der Figur sind deren beispielsweise 16 gemacht),
wobei man wieder, um genau zu verfahren, Pfloͤke eintreiben und
Loͤcher einbohren kann, und bezeichne die Theilpunkte mit Nummern dergestalt,
daß man ein Mal von oben nach unten und das andere Mal von unten nach oben
zaͤhlt; dann schlage man zwischen den Punkten, welche gleiche Nummern haben,
die Schnur; so wird dieselbe auf dem untergelegten Holz anzeichnen wo man
absaͤgen muß. –
Dabei sieht man denn, ob der Linien genug vorhanden sind, oder ob hin und wieder noch
welche zwischenzulegen sind, was leicht in der Witte vorkommen kann. In dem lezten
Fall, wie hier z.B. (Fig. 1.) zwischen 7 und 8 und zwischen 8 und 9, macht man Zwischenpunkte
in die Witte, bei 7 1/2 und 8 1/2 und verfaͤhrt damit wie vorher, bis sich
zeigt, daß man mit der Schnur nicht so genau mehr zwischenschlagen kann, als die
Saͤge hernach ausarbeiten kann.
Die kleinen Unebenheiten werden nach dem Absaͤgen beigerundet.
Zweite Classe.
Wenn hier Raum genug ist; so kann man wie bei der ersten Classe verfahren. Fehlt es
aber an Plaz; so kann folgendes dienen.
Man trage zuerst die Weite AB auf eine gerade Linie
(Fig. 2.)
und errichte in der Mitte von AB bei D die senkrechte DS,
als Hoͤhe. Dann berechne man sich die Brennweite
der Parabel, indem man die Weite AB mit sich
selbst multiplicirt, und das Product mit der sechszehnfachen Hoͤhe dividirt.
(Z.B. die Weite waͤre 10 Fuß und die Hoͤhe 4 Fuß; so waͤre die
Brennweite 100/64, d.h. 1 9/16 Fuß, oder die Weite waͤre 10 Fuß und die
Hoͤhe 2 Fuß; so waͤre die Brennweite 100/32, d.h. 3 1/8 Fuß u. s. w).
Diese Brennweite trage man auf die Hoͤhe und ihre Verlaͤngerung auf
beiden Seiten, von dem Scheitel S nach F und auch G (wodurch F der Brennpunkt wird). In
G ziehe man sodann eine unbestimmt
verlaͤngerte Linie HJ parallel zu AB (die Directrix).
Sodann nehme man vier Leisten, die etwas laͤnger seyn muͤssen als von
F bis A; lege sie auf
einander (Fig.
3.) und bohre an den Enden zwei Nagelbohrer senkrecht durch; nehme sie
sodann wieder aus einander und steke sie mit vier Bohrern oder angemessenen
Naͤgeln (f, g, k, l,) zu einem in den Winkeln
beweglichen Vierek (Fig. 4.) zusammen.
Den einen Winkelpunkt f befestige man nun in dem
Brennpunkt F, den gegenuͤber liegenden g aber befestige man nach und nach in verschiedenen
Punkten der Directrix HJ, und ziehe dann jedes Mal
zwischen k
und l eine gerade Linie, bis man so viel Linien hat, daß man
den Lehrbogen darnach ausschneiden kann.
Sollte hierbei der Raum wieder nicht hinreichen; so kann man sich dadurch noch
helfen, daß man die beiden Seiten gk und fk des Viereks noch etwas abkuͤrzt, so
jedoch, daß sie einander gleich bleiben (Fig. 5.); dann muß man
aber, wenn der parabolische Bogen auf einer Seite von GD (Fig.
2.) verzeichnet ist, das Vierek aus einander nehmen, um den Bogen auf der
anderen Seite zu beschreiben, und mit einer kuͤrzeren Linie lk vorlieb nehmen.
Zur Erlaͤuterung dieses Verfahrens dienen Fig. 6, 7 und 8., wo Parabeln von
einerlei Weite und verschiedenen Hoͤhen beschrieben sind, und wo namentlich
in Fig. 6. die
Seiten gk und fk
des Viereks abgekuͤrzt sind, dasselbe aber sodann hat umgestekt werden
muͤssen.
Dritte Classe.
Kommt hier der Fall vor, daß eine und dieselbe Parabel mehrmals hinter einander zu
verzeichnen ist; so finde ich es am bequemsten, die Construction wie bei der ersten Classe auf eine duͤnne und ebene
Messingplatte zu machen, die Linien mit dem Grabstichel zu ziehen, dann mit
Laubsaͤge und Feile auszuarbeiten, und nach dieser Lehre zu zeichnen.
Sollen aber mehrere Parabeln, die unter sich verschieden sind, construirt werden; so
kann man sich dazu eines eigenen Instrumentes bedienen (welches ich mir durch den
hiesigen Universitaͤts-Mechanikus Schubart
habe verfertigen lassen) und welches Fig. 9. abgebildet ist.
– A ist ein Brett, welches mit zwei
Schraubzwingen an dem Tisch oder dem Reißbrett befestigt wird. B ist eine darauf senkrecht befestigte Leiste, welche
bis gegen die Enden hin einen parallelen Schliz hat (der in der Figur verdekt ist).
C ist ein Arm, welcher vermittelst einer Schulter
und eines durch den Schliz gestekten Fortsazes sich an B
geradlinig hin und her bewegen laͤßt; selbst aber wieder einen Schliz hat,
welcher senkrecht auf der Linie der Bewegung steht. DD sind zwei auf B festgeschraubte Stangen,
welche da wo sie zusammenkommen, einen senkrecht abwaͤrts gehenden in der Axe
durchbohrten Cylinder tragen, der uͤber den Brennpunkt zu stehen kommt. fkgl ist ein
aus Messingschienen bestehendes, in den Winkeln verschiebbares Parallelogramm. k und l sind die Charniere,
welche nicht nur die Schienen zusammenhalten, sondern auch das aufgeschlizte Lineal
kl tragen, welches nahe doppelt so lang ist,
als eine der Schienen des Parallelogramms. Das gleichfalls in der Axe durchbohrte
Charnier g wird durch Schulter und Gegenschraube an
einem beliebigen Punkt des Schlizes in C festgestellt,
und beschreibt also, wenn C bewegt wird, die Directrix.
m ist ein Rohr, welches sich sowohl in dem Schlize von C als auch in dem geschlizten Lineal kl verschieben laͤßt, und also die Parabel
beschreibt.
Um nun hiermit eine Parabel von bestimmter Brennweite zu zeichnen, stekt man durch
die Loͤcher bei m, f und g drei Stahlstifte (welche sonst bei m', f'
und g' ihren Plaz finden), verschiebt so lange bis m, f und g in eine gerade
Linie kommen, welches man an den durchgestekten Stiften genau erkennen kann,
loͤst dann die Gegenschraube bei g und schiebt
g in dem Schliz von C so
lange hin und her, bis m von g und f um die verlangte Brennweite absteht,
(und also dem Scheitel entspricht). Dann stellt man g
durch die Gegenschraube wieder fest, nimmt die Stifte weg, befestigt das Instrument
mit den Schraubzwingen, so daß f uͤber dem
Brennpunkt, und m uͤber dem Scheitel steht, faßt
mit einer Hand den Arm C und mit der anderen den bei m durchgestekten Zeichenstift, und schiebt sowohl C an B, als auch m in C und kl leise fort, so muß der Zeichenstift die
verlangte Parabel beschreiben.
––––––––––––
Im Vorhergehenden ist absichtlich immer vorausgesezt, daß die Weite AB und die Hoͤhe DS vorgegeben sey, weil dieses der Fall ist,
welcher dem praktischen Arbeiter wohl am oͤftersten vorkommt.
Naͤchstdem wird wohl auch der Fall ziemlich haͤufig vorkommen, daß die
Weite AB und der Brennpunkt F (Fig.
2.) vorgegeben ist; in diesem Fall braucht man nur zu wissen, daß F von A oder B immer eben so weit absteht als die Directrix HJ
von der Grundlinie AB; man wird also in
diesem Falle FA zu messen und DG = FA
aufzutragen, sodann aber FG zu halbiren haben, um
den Scheitel S zu bekommen, und nach dem Vorhergehenden
den Lehrbogen zu zeichnen.
Endlich kommt auch wohl der Fall vor, daß außer der Grundlinie AB noch die Brennweite FS
gegeben ist, und man die Hoͤhe DS
erst daraus zu finden hat. In diesem Falle berechnet man diese Hoͤhe, indem
man die Weite mit sich selbst multiplicirt, und das Product mit der sechszehnfachen
Brennweite dividirt (z.B. die Weite AB
waͤre 12 Fuß, die Brennweite 1 1/2 Fuß; so haͤtte man die Hoͤhe
6 Fuß).
–––––––––––––
Außer diesen einfachen Faͤllen, wobei immer die Weite oder Grundlinie AB als vorgegeben vorausgesezt wird,
koͤnnen aber bei der Parabel noch mehrere Faͤlle vorkommen, wo die
Weite nicht gegeben ist, sondern statt dessen bloß der Scheitel, die Richtung der
Axe und ein Punkt; oder der Scheitel und zwei Punkte; oder die Brennweite und drei
Punkte; oder vier einzelne Punkte und dergl. mehr.
Unter diesen zusammengesezteren Aufgaben scheint nur einer fuͤr den
praktischen Arbeiter, insbesondere den Bauhandwerker, vorzuͤglich wichtig zu
seyn, welcher also hier noch abgehandelt werden soll.
Wenn naͤmlich (Fig. 10.) eine
horizontale Linie QK vorgegeben ist, in welche der
Scheitel einer Parabel fallen soll, und man uͤberdieß nur weiß, daß die
Parabel durch die Punkte A und C gehen soll, welche in verschiedenen Tiefen Aa und Cc unter der Horizontale liegen
(wie z.B. wenn zwischen den Widerlagen A und C ein unsymmetrisches parabolisches Gewoͤlbe zu
machen waͤre, das seinen Scheitel zwischen a und
c irgendwo in QK
haben sollte); so kommt die Axe außer der Mitte zu stehen, und man muß also die
Punkte D und S auffinden,
damit man AD gleich DB machen und aus A, S und B die Parabel nach dem obigen so verzeichnen
koͤnne, daß sie auch durch C geht. – Hier
muß man nun zuerst durch A eine Horizontale legen, bis
sie bei a' in die Senkrechte durch C eintrifft, und dann Aa
' in D gehoͤrig
eintheilen. – Dieses gehoͤrige Eintheilen geschieht
durch Rechnung, wenn man Aa
' nach der Gesellschaftsrechnung so eintheilt, daß sich
AD und Da
' zu einander verhalten wie die Quadratwurzeln aus den
Tiefen Aa und Cc; oder
durch Zeichnung, wenn man die Tiefe Cc in die Verlaͤngerung der Senkrechten Aa nach ac
' traͤgt; dann Ac
' in m halbirt, und mit mA oder mc
' den Halbkreis beschreibt, der die Horizontale des
Scheitels in n schneidet. Traͤgt man sodann an in die andere Senkrechte nach a'n' unter die Horizontale durch A, und zieht an
'; so bestimmt der Durchschnitt den Punkt D.
Sobald D gefunden ist, kann man den Scheitel S entweder durch bloßes Abloͤthen uͤber
D bestimmen, oder man kann auch (was in der Figur
nicht gezeichnet ist) an noch ein Mal uͤber
Cc in die Hoͤhe tragen, und nach A eine gerade Linie ziehen, die dann durch S gehen muß.
Will man endlich, ehe man mit Beschreibung des Lehrbogens fortfahrt, sich noch
versichern, daß man die Zeichnung fuͤr die Axe gewiß richtig gemacht hat; so
braucht man nur an unter A nach Ao, und unter C nach Cn zu tragen,
und die drei (in der Figur punktirten) Linien oc,
an und AC zu
ziehen; welche sich alle drei in einem Punkt der Are schneiden muͤssen.
–––––––––––––
Von dem Arbeiter, der seine parabolischen Lehrboͤgen selbst vorzuzeichnen
versteht, koͤnnte man endlich noch verlangen, daß er auch die auf die Parabel
winkelrechten Linien (Normalen) selbst zeichne, in
welchen z.B. die Lagerfugen eines parabolischen Gewoͤlbes zu liegen kommen, wenn
naͤmlich solche, wie gemeiniglich der Fall seyn wird, winkelrecht auf den
Bogen verlangt werden. (Wer zu besonderen Zweken anders gestellte Lagerfugen
verlangt, muß sie selbst vorschreiben.) Dazu dient nun folgende Regel: Man berechne
sich zuerst, wie oben gezeigt worden ist, die Brennweite FS der Parabel (Fig. 11.). Soll nun in
C eine Normale gezogen werden, so messe man die
Tiefe Cc unter der Horizontale des Scheitels,
mache Sc
' gleich Cc und nehme
c'n gleich der doppelten Brennweite; so ist nC die Richtung der winkelrechten Lagerfuge durch
C.
Tafeln