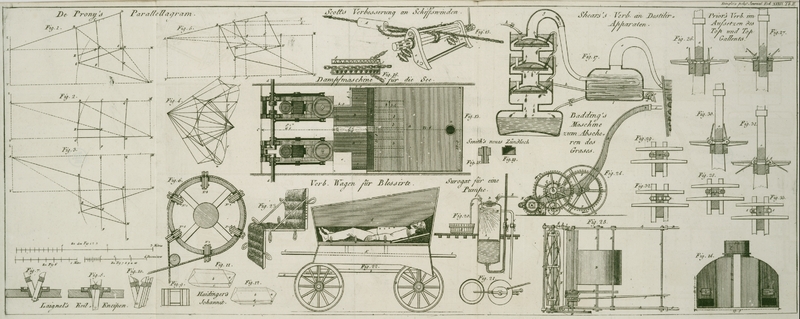
| Titel: | Ueber das Parallelogramm am Wagebalken der Dampfmaschine. Von Hrn. de Prony. |
| Fundstelle: | Band 39, Jahrgang 1831, Nr. XXIX., S. 82 |
| Download: | XML |
XXIX.
Ueber das Parallelogramm am Wagebalken der
Dampfmaschine. Von Hrn. de
Prony.
Aus dessen Rapport sur la nouvelle machine du Gros. Caillou. p. 81. im Bulletin d. Scienc.
technol. Juillet . 1830. S. 256.
Mit Abbildungen auf Tab.
II.Wir haben im Polyt. Journ. Bd. XXXV. S. 262. u. 332. die Ansichten der englischen
Mathematiker uͤber diesen Gegenstand mitgetheilt; es ist der Muͤhe
werth, hier auch die Ansichten eines der ersten Mathematiker Frankreichs, Hrn.
de Prony's, vorzulegen. A. d. Ue.
de Prony, uͤber das Parallelogramm am Wagebalken der
Dampfmaschine.
Das oberste Ende der Staͤmpelstange des Cylinders der Dampfmaschine, welches
an einem der Winkel des Parallelogrammes des Wagebalkens haͤngt, beschreibt
in seinem Laufe (Fig. 4.) einen Bogen, st, einer
eifoͤrmigen krummen Linie, rstuvr (s. Architecture hydraulique. 2. Theil. Paris. 1790. Art.
1483. u. 1492.), und dieser Bogen, auf welchem sich ein Einbiegungspunkt (point d'inflexion) beinahe in der Mitte seiner
Laͤnge befindet, weicht, wenn die Verhaͤltnisse des Apparates
gehoͤrig beobachtet sind, sehr wenig von der zwischen ihren Endepunkten, s und t, gezogenen geraden
Linie ab. Ich will hier die Formeln aufstellen, mittelst deren man die
Verhaͤltnisse zwischen den verschiedenen Lagen des obersten Punktes dieser
Staͤmpelstange und den Bewegungen bestimmen kann, welche die uͤbrigen
Theile des Systemes einschlagen, wenn der Winkel, welchen die Achse des Wagebalkens
mit der Senkrechten oder mit der Horizontalen bildet, veraͤndert wird. Ich
werde auch die Verhaͤltnisse zwischen den Groͤßen jener Theile der
Maschine betrachten, deren Einrichtung sich gewissen Bedingungen unterziehen
laͤßt.
Diese Formeln, welche in der Anwendung weit bequemer sind, als jene, die ich im J.
1790 in meiner Abhandlung „des Machines à
feu“ bekannt machte, werden auch auf die Maschine in dem
gegenwaͤrtigen Berichte angewendet werden.
A und K (Taf. II. Fig. 5.) sind
die beiden feststehenden Mittelpunkte der Umdrehung des ganzen Systemes. BDHG, BCFE sind
das kleine und große Parallelogramm. AD und GK sind die geraden Linien, welche sich jede um
ihren feststehenden Punkt A und
K als Mittelpunkt in der senkrechten Flaͤche
drehen, welche diese Parallelogramme enthaͤlt. H
und F sind die Punkte der gegliederten
Aufhaͤngungen der Staͤmpelstangen.
Ich ziehe die Horizontalen CX, BX, AM, mH, VK, und die
Senkrechten AV, Cc, Ff, Dd, QH, MK. Diese Entwurfslinien werden die Erweisung der Formeln denjenigen
erleichtern, die sich von der Genauigkeit derselben uͤberzeugen wollen.
AB = ς;
GK = r;
AM = h;
AV = k;
BG = a;
BD = b;
BE = a';
BC = b';
AQ = x;
QH = γ;
Aq = x;
qF = y'.
Winkel DAM = α.
Hiernach berechnen sich die Werthe
(1) Textabbildung Bd. 39, S. 83
(2) Textabbildung Bd. 39, S. 83
und man erhaͤlt die horizontalen und senkrechten
Coordinaten der obersten Punkte H und F der Staͤmpelstangen des großen und kleinen
Cylinders auf ihren feststehenden Ursprung, A,
zuruͤkgefuͤhrt durch die Formeln
(3)
x = a cos.
δ + (b + ς) cos. α; y = a sin.
δ – (b + ς) sin.
α
x' = a' cos.
δ + (b' + ς) cos.
α; y' = a' sin. δ – (b + ς) sin. α.
Diese allgemeinen Werthe sind unabhaͤngig von allen besonderen
Verhaͤltnissen zwischen den Laͤngen der Seiten der großen und kleinen
Parallelogramme; sie sezen nur die Parallelismen a und
a', b und b' voraus. Man
kann aber eine hoͤchst vortheilhafte Bedingung fuͤr praktische
Anwendung anbringen, welche die Berechnung von x' und
y' abkuͤrzt. Diese Bedingung besteht darin,
daß man die Verhaͤltnisse
a/a', b/b' gleich stellt, wodurch dann immer in allen Lagen der
Parallelogramme der feststehende Mittelpunkt A und die
beweglichen Aufhaͤngepunkte F und H sich in einer und derselben Geraden befinden werden.
Sezt man dann
(ς' + b')/(ς + b)
= μ,
so erhaͤlt man (4) x' = μx; y' = μy.
Diese Formeln lassen sich unmittelbar zur Berechnung der Bewegungen der obersten
Punkte der Staͤmpelstangen in einem gegebenen Systeme anwenden; man kann sich
derselben aber auch mit Nuzen zur Bestimmung gewisser Verhaͤltnisse bedienen,
wenn man eine Maschine bauen will, welche besondere Bedingungen erfuͤllen
soll. Es ist bequem, als gemeinschaftliche Bedingungen bei allen Entwuͤrfen
solcher Maschinen zu betrachten: 1) die Horizontalitaͤt der Linie, welche
durch den feststehenden Mittelpunkt A der Umdrehung, und
durch den obersten Punkt H der Staͤmpelstange in
der weitesten Entfernung von A in ihrer oberen
anfaͤnglichen Lage laͤuft. 2) die Gleichheit der Verhaͤltnisse,
auf welcher obige Gleichungen (4) beruhen, und aus welchen folgt, daß die Punkte A, F und H, immer in einer
und derselben geraden Linie sind. 3) Gleichheit der Winkel, welche von der
Horizontalen, AM und von der Achse AD des halben Wagebalkens in den aͤußersten
Lagen desselben, der oberen und der unteren, gebildet werden.
Nach diesen vorlaͤufigen Eroͤrterungen wird man nun das System in drei
bestimmten Lagen des Wagebalkens betrachten, d.h., in seinen beiden
aͤußersten Lagen, der oberen und der unteren, und in seiner mittleren Lage,
durch welche seine Achse horizontal wird. Wenn man durch 2 A
den gesammten Winkel bezeichnet, welchen diese Achse zwischen den
aͤußersten Lagen beschreibt, so liefern die Gleichungen (1) (2) (3) und (4)
drei Gruppen, welche mit α = A, α = o, α =
– A correspondiren, und geben so Mittel an die
Hand, Verhaͤltnisse zwischen den Theilen des Systemes herzustellen, wie die
aufgestellten Bedingungen sie fordern. Es wird also die senkrechte Sehne des Winkels
2 A
, der von dem Halbmesser AD beschrieben wird,
von einer solchen Laͤnge seyn muͤssen, daß sie dem Laufe des
Staͤmpels gleich ist; es wird vor Allem nothwendig seyn, daß die Werthe von
x, die aus den 3 Gruppen erhalten werden, entweder
einander wirklich oder beinahe gleich seyen; daß von den correspondirenden Werthen
von y der erste = o, und der
zweite beinahe die Haͤlfte des dritten sey, der den ganzen Lauf bemißt. Man
wird sehr bald sehen, daß die Maschine Edward's diesen
Bedingungen auf eine hoͤchst genuͤgende Weise entspricht.
Ich beschraͤnke mich hier auf diese allgemeinen Angaben, und seze nur den
Formeln (1) (2) und (3) die folgenden bei, welche sich vorzuͤglich auf die
anfaͤngliche obere Lage des Wagebalkens anwenden lassen.
Ich seze (Fig.
1.)
den anfaͤnglichen Winkel DAM = A; AD = b + ρ = m; AH = n.
Die Senkrechte Dd = q;
Ad = p; dH = p'.
Hieraus erhaͤlt man die Verhaͤltnisse
(5)
p = m cos. A: p' =
(a² – q²) 1/2 = (a² –
m² sin². A) 1/2
q = m sin. A:
m² + n² – 2 mn cos. A – a² = o.
Im Falle, wo man A durch m, n
und a zu bestimmen haͤtte, koͤnnte man
folgende Formeln anwenden:
(6) Textabbildung Bd. 39, S. 85
Die Verhaͤltnisse, welche von den Dimensionen und von der anfaͤnglichen
Lage des Parallelogrammes BDHG abhaͤngen,
muͤssen sich mit der Laͤnge und anfaͤnglichen Lage des
Halbmessers GK = r
vertragen, welcher, waͤhrend er sich um den festen Mittelpunkt K dreht, mit seinem anderen Ende an der Gliederung am
Winkel G des Parallelogrammes angebracht ist. Hier die
Formeln, welche die von diesem Halbmesser abhaͤngenden Werthe mit den vorigen
Werthen verbinden.
Man hat, in Bezug auf die horizontale und senkrechte Coordinate des Punktes G (Fig. 1.), die respectiven
Werthe auf den Ursprung K
zuruͤkgefuͤhrt.
(7)
ξ = h –
ρ cos. A – (a²
– m² sin². A) 1/2
η = k
– b sin. A,
welche die Elemente der Rechnung
r = (ξ + η²) 1/2
liefern; folgende Formel gibt aber einen Werth von r, der unmittelbar an die anfaͤngliche Lage des
Punktes H, und an die festen Lagen M und K gebunden ist. Es
seyen
die Winkel
KHM = E
GHK = 180° – (A + E) = λ
KH = S,
so erhaͤlt man
(8)
Tang. E = k/(h – n); S = k/(sin. E) = (h – n)/cos. E.
r = (4 bs
sin.² (1/2 λ) + (b – s)²) 1/2.
Man kann die vorhergehenden Formeln oder einen Theil derselben auf das unter vorigem
Verhaͤltnisse beschriebene System anwenden.
Dieses System ist immer nach der Bedingung, a/a' = b/b' eingerichtet, nach welcher man die Gleichungen (4) erhielt. Die obersten
Punkte der Staͤmpelstangen, und der feststehende Mittelpunkt der Umdrehung
A befinden sich immer in derselben geraden Linie,
welche in ihrer anfaͤnglichen Lage (Fig. 1. Taf. II.)
horizontal ist; uͤberdieß ist in dieser anfaͤnglichen Lage der
Scheitel D des oberen Winkels des großen
Parallelogrammes, und der feststehende Mittelpunkt der Umdrehung k in derselben senkrechten Entfernung von der
Horizontalen AM, indem einer oben, der andere
unten durch den feststehenden Mittelpunkt der Umdrehung durchgeht, und diese
Horizontale AM theilt den gesammten Winkel 2 A
, welcher von dem halben Balken AB
waͤhrend eines ganzen Laufes des Staͤmpels beschrieben wird, in zwei
gleiche Theile: alle diese Anordnungen sind sehr gut getroffen.
Wenn man nun als Daten annimmt (Fig. 1. Taf. II.)
AD = m; AC = ρ + b; AB = ρ; DH = a; AH = n,
Laͤngen, deren Zahlenwerthe oben an der Tafel
geschrieben stehen;Dieß ist in unseren Exemplaren nicht der Fall. Es ist nur der Maßstab
angegeben.A. d. Ue. so kann man sogleich die Werthe von AF und
CF bestaͤtigen, welche die durch die
Gleichungen (4) verlangte Bedingung herstellen, und man findet
AF = 1m,7951; CF = 0m,55809.
Wenn man nach denselben Daten den anfaͤnglichen Winkel DAH = A, entweder nach
der lezten Gleichung (5), oder nach einer der lezten Gleichungen (6) berechnet, so
findet man
A = 17°35'30''; woraus Dd = m sin. A = 0m,76011.
Man haͤtte den Winkel A viel einfacher erhalten,
wenn man als Datum, statt DH = a, die Senkrechte Dd
genommen haͤtte, welche, nach einer der oben ausgesprochenen Bedingungen,
gleich seyn muß Mk oder k, d.h. fast dem Werthe des halben Laufes des Staͤmpels, und die
Seite DH wuͤrde aus diesem Werthe und aus
den uͤbrigen Daten geschlossen worden seyn.
Da die Groͤße und die Lage des Parallelogrammes BDHG bekannt sind, so wie die Lage der Horizontalen Vk, welche durch die Bedingung Dd = Mk gegeben
ist, so laͤßt sich die Lage des unbeweglichen Mittelpunktes k dadurch bestimmen, daß man entweder den Halbmesser Gk = r, oder den
Abstand AM = h als
gegeben annimmt, wornach HM = h – n.
Nimmt man als gegeben h = 3m,022, so hat man HM = 0m,571, woraus
Textabbildung Bd. 39, S. 87
und zulezt GK = r = 1m,712.
Ich gehe zu der wichtigen Eigenschaft des Apparates uͤber, naͤmlich zur
beinahe geradlinigen Bewegung des obersten Punktes der Staͤmpelstange, und
ich nehme zuvoͤrderst diesen Punkt in der Mitte seines Laufes an, wann der
halbe Wagbalken AD in die horizontale Lage auf die
Linie AM (Fig. 2. Taf. II.) kommt.
In diesem Falle hat man, Gleichungen (1) (2) (3),
β = 24°, 43', 50'';
c = 1m,8166;
γ = 69°, 56', 00''
δ = 94°, 39', 50'';
x = 2m,453;
y = 0m,7595.
Die Abweichung in horizontaler Richtung, oder die Entfernung aus der Senkrechten, die
durch den Anfangspunkt laͤuft, ist ungefaͤhr 2 Millimeter, oder 1/360
des halben Laufes, und der Werth von y ist nicht
merklich von dem Werthe von k verschieden.
Sezen wir endlich der Staͤmpel sey am Ende seines Laufes, oder der oberste
Punkt der Stange sey auf die Horizontale Vk
herabgelangt (Fig.
3., Taf. II.); so hat man, in diesem Falle, nach den oben angezeigten
Bedingungen
α = – A =
– 17°, 35', 30''; β = 11°,
23', 20'';
c = 1m,7488; γ = 74°, 36', 20''; δ = 85°, 59', 40'':
woraus x = 2m,4508; y = 1m,5202.
Die Abweichung, in Hinsicht auf die Senkrechte, die durch den Anfangspunkt
laͤuft, ist hier auf 1/5 Millimeter reducirt, und der Werth von y ist so ziemlich der ganze beabsichtigte Lauf: dieß ist
alle Genauigkeit, die man verlangen kann.
Nach diesen Werthen wird man die Lage des obersten Punktes der Stange des kleinen
Parallelogrammes aus den Gleichungen (4) (auf das System angewendet, um welches es
sich handelt) sehr leicht berechnen koͤnnen; und man hat am Ende des
Laufes
x' = (ς + b')/(ς + b) x =
1,842/2,515 × 2m,4504 =
1m,7947.
y' = (ς + b')/(ς + b) y =
1,842/2,515 × 1m,52044 = 1m,114.
Die Abweichung von der Senkrechten, die durch den Anfangspunkt
laͤuft, ist fuͤr den ganzen Lauf nicht mehr als 3/10 Millimeter. Die
Uebereinstimmung der Maße, so wie diese durch Berechnung abgeleitet sind, und wie
sie unmittelbar auf der Maschine genommen und in meinem Berichte verzeichnet
sind, ist eine sichere Gewaͤhr der Genauigkeit meiner Verfahrungsweise.
Ich habe in dem Vorausgegangenen die Rechnung angewendet, als das einzige Mittel,
mittelst dessen man die vollkommenste Genauigkeit erlangen kann, sowohl in Hinsicht
auf Pruͤfung desjenigen, was bereits geschah, als auf den Entwurf desjenigen,
was man ausfuͤhren will: indessen wird man sich immer der graphischen Methode
mit Vortheil bedienen, wenn man sorgfaͤltig entweder in natuͤrlicher
Groͤße oder in sehr großem Maßstabe zeichnet. So wird man, z.B., wenn man das
System ABDHG, Fig. 3. haͤtte, das
sich um den festen Punkt A dreht, mit Gliederung in B, D, H und G, und man den
Punkt H eine Linie wollte durchlaufen lassen, die wenig
von der senkrechten QH abweicht, einen Entwurf in
natuͤrlicher Groͤße (épure)
zeichnen, in welchem dieses System drei Lagen hat, in deren zwei der Punkt H an die aͤußersten Enden, und in deren dritten
er in die Mitte seines Laufes kommt, in derselben Senkrechten. Diese drei Lagen des
Systemes werden drei correspondirende des Punktes G
liefern. Fuͤhrt man einen Kreis durch diese drei lezten Punkte, so wird man
den festen Mittelpunkt k finden, und den Halbmesser kG, indem man die Bedingung erfuͤllt, die
Bewegung des Punktes H so zu reguliren, daß er sich von
Q bis H drei Mal in
derselben Senkrechten befindet, von welcher er sich in den uͤbrigen Punkten
wenig entfernen wird, wenn anders seine Verhaͤltnisse gehoͤrig
getroffen sind. Durch Rechnungen gelangt man leicht zu demselben Resultate; ich
halte mich aber an diese allgemeinen Anzeigen, und habe Grund zu hoffen, daß das
hier eingeschlossene Detail den Mechanikern nuͤzlich seyn wird, die
uͤber ihre Entwuͤrfe nachdenken wollen.
Tafeln