| Titel: | Ueber die Anwendung der hydraulischen Kreisel oder der Wasserräder mit krummen Bélidor'schen Schaufeln im Großen, in den Hüttenwerken und Manufacturen; von Hrn. Fourneyron, Civilingenieur zu Besançon. |
| Fundstelle: | Band 53, Jahrgang 1834, Nr. XLII., S. 241 |
| Download: | XML |
XLII.
Ueber die Anwendung der hydraulischen Kreisel
oder der Wasserraͤder mit krummen Bélidor'schen
Schaufeln im Großen, in den Huͤttenwerken und Manufacturen; von Hrn. Fourneyron, Civilingenieur zu
Besançon.Man vergleiche uͤber diese Wasserraͤder auch die fruͤher im
Polytechn. Journale Bd. XLVIII. S. 95,
und Bd. LI. S. 6 erschienenen
Abhandlungen.A. d. R.
Aus dem Bulletin de la Société
d'encouragement. Januar 1834, S. 3; Februar S. 49, und Maͤrz S.
85.
Mit Abbildungen auf Tab.
IV und V.
Anwendung der hydraulischen Kreisel oder der Wasserraͤder
mit krummen Bélidor'schen Schaufeln im Großen etc.
Vorlaͤufige Betrachtungen.
Da die Apparate oder sogenannten Wasserraͤder, die man bisher anwandte, um die
Kraft des Wassers, welches entweder von einer gewissen Hoͤhe
herabfaͤllt oder eine gewisse Geschwindigkeit besizt, zu sammeln, alle ihre
besonderen Vortheile und auch ihre von diesen unzertrennlichen Nachtheile besizen,
so eigneten sie sich nicht zu allen Zweken gleich gut. So koͤnnen gewisse
Raͤder, welche sehr geeignet sind, um Wasser zu ersparen und sehr große
Dimensionen haben, nur bei sehr großen Gefallen angewandt werden und nur eine
gewisse Geschwindigkeit erlangen, andere hingegen, welche bei kleinem Gefalle
anwendbar sind und sich mit einer groͤßeren Geschwindigkeit bewegen
koͤnnen, erfordern eine viel groͤßere Wassermenge, als man sich zu
jeder Zeit verschaffen kann; eine dritte Art endlich, welche die Vortheile der
ersten und die Nachtheile der zweiten Art theilt, wird ihnen bisweilen in der Praxis
vorgezogen.
Bei diesen wenigen Mitteln, dem Wasser seine Kraft zu entziehen, um sie auf die in
den Fabriken erforderlichen mechanischen Organe zu uͤbertragen, hat man eine
große Menge von Anordnungen ersonnen, welche sich den drei genannten Arten von
Wasserraͤdern mehr oder weniger naͤhern und groͤßten Theils
keine sehr bemerkenswerthe Verbesserungen darbieten. Aus diesen Bemuͤhungen
ging z.B. das Rad des Hrn. Poncelet hervorEine ausfuͤhrliche Beschreibung dieses Rades ist im Bd. XIX. S. 447 etc. und auf Tab. X
des Polyt. Journ. die Abbildung desselben enthalten. Auch findet man in den
darauf folgenden Baͤnden weitere Bemerkungen und Erfahrungen
uͤber diese senkrechten unterschlaͤchtigen Raͤder mit
krummen Schaufeln.A. d. R., welches sich wesentlich von allen anderen unterscheidet und nach den
theoretischen Untersuchungen und den Versuchen seines Erfinders nuͤzliche
Resultate zu versprechen scheint, wenn es nach den von diesem Gelehrten
vorgeschriebenen Regeln angewandt wird. Derselben Ursache muß man auch die
theoretischen Untersuchungen der HH. Navier und Burdin uͤber die unter der allgemeinen Benennung
hydraulische Kreisel (turbines
hydrauliques) bekannten Wasserraͤder zuschreiben.
Da sich aus den Untersuchungen der Mechaniker, welche sich mit der Verbesserung der
Wasserraͤder beschaͤftigten, ergab, daß die sogenannten
Kreiselraͤder große Vortheile darbieten wuͤrden, wenn man eine den
Angaben der Theorie angemessene Einrichtung derselben erfinden wuͤrde, so hat
die Société d'encouragement auf die
Loͤsung dieses Problems einen Preis ausgeschrieben und die Dauer des
Concurses wurde auch bereits mehrmals verlaͤngert. Ich bin seit dem Jahre
1823 mit dieser Aufgabe beschaͤftigt, stellte aber meine ersten Versuche,
welche mit einem uͤber alle Erwartung guͤnstigen Erfolg
gekroͤnt wurden, erst im Jahre 1827 an; da das von mir gebaute Proberad
jedoch das einzige von dieser Art war, so konnte ich bei dem Concurse von 1827 nicht
auftreten. Arbeiten anderer Art gestatteten mir auch nicht im Jahre 1829 unter die
Preisbewerber zu treten und ich bemuͤhte mich daher, im Jahre 1832 zum
Concurse zugelassen werden zu koͤnnen.
Das Programm verlangte, daß wenigstens zwei Raͤder erbaut und im Großen
angewandt seyn muͤssen: ich hatte aber nur ein solches, welches mit
offenbarem Vortheile zum Treiben einer Drehebank, einer Mahl- und einer
Saͤgemuͤhle benuzt wurde; die Bedingung des Programms war also nicht
erfuͤllt. Hinsichtlich einer zweiten Anwendung meines Rades bestand die
groͤßte Schwierigkeit nicht in der Loͤsung des vorgesezten Problems,
sondern darin, den Widerstand zu uͤberwinden, womit neue Ideen allgemein
angenommen werden.
Endlich war ich so gluͤklich, die Bekanntschaft des Herrn Caron zu machen, welcher das Geblaͤse fuͤr
seinen Hochofen zu Dampierre in der Franche-Comté durch ein
aͤhnliches Kreiselrad zu treiben wuͤnschte, wie ich eines an den
Eisenwerken zu Pont-sur-l'Ognon errichtet hatte.
Ich verfertigte sogleich ein solches Rad von der Kraft von sieben bis acht
Dampfpferden, ganz aus Schmiede- und Gußeisen; die Vorzuͤge dieses
Rades, welches sich unter Wasser dreht, eine groͤßere nuͤzliche
Wirkung liefert, als die besten unterschlaͤchtigen Raͤder, dabei
solider, dauerhafter, und weniger unguͤnstigen Zufallen ausgesezt ist,
veranlaßten Hrn. Caron, zwei bereits fuͤr ein
Geblaͤse eines neuen Hochofens erbaute große Raͤder liegen zu lassen,
und derselbe forderte
mich auf, ihn an Statt dieser zwei ungeheuren hoͤlzernen Raͤder ein
großes Kreiselrad zu verfertigen.
Dieses ganz aus Schmiede- und Gußeisen verfertigte Kreiselrad ist erst seit
ungefaͤhr anderthalb Monaten vollendet. Es sollte fuͤr eine Kraft von
zwanzig Dampfpferden hergestellt werden, da aber der Eigenthuͤmer den Plan
hatte, dieselben Modelle zur kuͤnftigen Errichtung eines Rades von
ungefaͤhr fuͤnfzig Pferdekraͤften zu benuzen, so nahm ich
keinen Anstand diesem Rade eine viel groͤßere Kraft zu geben, als der
gewoͤhnliche Bedarf erfordert, weil diese groͤßere Kraft bei dem
bedeutenden Steigen und Fallen des Doubs ein Mittel liefert, daß man nicht so vielen
Unterbrechungen der Arbeit ausgesezt ist, wie bei den alten Raͤdern, welche
sehr oft unter Wasser getaucht sind. Ich pruͤfte daher mein Kreiselrad
mittelst des Prony'schen Zaumes (Kraftmessers), wobei
sich ergab, daß es bei einem Gefalle von 1,30 Meter eine der Kraft von
fuͤnfzig Dampfpferden gleiche Wirkung ausuͤben kann.
Die Errichtung dieser drei Raͤder hatte bereits den Erfolg, daß ich mehrere
Auftrage auf aͤhnliche erhielt. Da das Kreiselrad zu Fraisans wie die vorher
von mir hergestellten tief unter dem Wasser arbeitet und selbst wenn ihm nur 0,227
Meter (8 Zoll 5 Linien) Gefaͤlle blieben, so habe ich in jeder Hinsicht den
Anforderungen des Programms der Société
d'encouragement entsprochen.
Erster Theil. Theorie und allgemeine Beschreibung
der hydraulischen Kreisel.
1) Die Aufgabe, welche zu loͤsen ist, wenn man von einem Wasserfall die
moͤglich groͤßte Wirkung erzielen will, besteht bekanntlich darin, daß
man das Wasser ohne Stoß in dem zur Fortpflanzung seiner Kraft bestimmten Apparate
auffaͤngt und es aus demselben ohne Geschwindigkeit austreten
laͤßt.
Diese Bedingungen, welche leicht zu erfuͤllen waren, wenn es sich nur von
einem fluͤssigen Faden oder duͤnnen Strahle handeln wuͤrde,
bieten in der Praxis unuͤbersteigliche Hindernisse dar. Eine Wassermasse,
deren Dimensionen etwas betraͤchtlich sind, verhaͤlt sich nicht wie
ein einfacher Strahl, sondern bietet bei ihrer Bewegung unendlich viele
Umstaͤnde dar, welche wohl beruͤksichtigt werden sollten.
Da mehrere der bei der Bewegung der Fluͤssigkeiten Statt findenden
Erscheinungen der Beobachtung entgehen, waͤhrend andere nicht berechnet
werden koͤnnen, weil wir die Geseze, nach denen sie erfolgen, nicht genau
kennen, so muß man bei dem gegenwaͤrtigen Zustande unserer Kenntnisse sich so
viel als moͤglich dem Maximum zu naͤhern suchen, obgleich man wenig Hoffnung hat,
es vollstaͤndig zu erreichen.
Diese Richtung habe ich meinen Untersuchungen gegeben, deren Resultate die Probe der
Erfahrung bereits bestanden haben.
2) Es sey AB ein einfacher fluͤssiger
Strahl, welcher einen Winkel ABC = a mit einer senkrechten Ebene BD macht, die mit sich selbst parallel in der
Richtung BE beweglich ist, welche auf BC und BD
senkrecht ist. (Fig.
1 auf Taf. IV.)
Wir wollen nun annehmen, der Strahl AB, welcher
horizontal auf die Ebene BD wirkt, besize eine
Geschwindigkeit V, und untersuchen, was
geschaͤhe, wenn die Ebene BD der Wirkung
des Wassers, welches sie in Bewegung zu sezen strebt, keinen Widerstand darbieten
wuͤrde. Es ist offenbar, daß, wenn man von allem Widerstaͤnde
abstrahirt, der fluͤssige Strahl sich so bewegen wird, als wenn die Ebene BD nicht vorhanden waͤre, und leztere eine
solche Geschwindigkeit annehmen wird, daß sie den Raum DD' in derselben Zeit durchlaͤuft, in welcher ein Wassermolecul,
das die Geschwindigkeit V besizt, BD' durchlaͤuft.
Wenn also v die Geschwindigkeit der beweglichen Ebene BD bezeichnet, so hat man
V : v = BD' : DD'.
Und da BD senkrecht auf DD' und dieses parallel mit BB' ist, so ist das Dreiek BDD, bei D
rechtwinklicht. Man hat also
DD' = BD', sin. (DBD' = sin. a);
sezt man diesen Werth von DD' in die Proportion, so hat man
V : v = BD': BD' sin. a, woraus sich ergibt
V sin. a = v.
Das heißt, wenn die bewegliche Ebene senkrecht auf die
Richtung der Bewegung ist, so ist die groͤßte Geschwindigkeit, welche ihr das
Wasser ertheilen kann, gleich der eigenen Geschwindigkeit dieser
Fluͤssigkeit, multiplicirt mit dem Sinus des Winkels ABC, welcher mit a
bezeichnet ist.
3) Man ertheile nun der beweglichen Ebene BD eine
andere Lage, z.B. die Lage Bd; wenn diese neue
Ebene durch den Strahl AB, welcher immer dieselbe
Geschwindigkeit V besizt, in Bewegung gesezt wird, so
reicht es hin, – damit das Wasser nicht aus seiner Richtung AB kommt und folglich auf die Ebene keine andere
Wirkung als die ausuͤbt, daß es auf sie die moͤglich groͤßte
Geschwindigkeit uͤbertraͤgt, – dazu, sage ich, reicht es hin,
daß die Ebene den Raum dD' durchlaufen hat,
waͤhrend ein Wassermolecul von B nach D' gelangt ist. Diese Veraͤnderung hatte also zur
Folge, daß um die
Groͤße Dd die vorhergehende Geschwindigkeit
v = V sin. a vermindert
wurde.
Wenn der Winkel ABd, welchen die Ebene mit der
Richtung des Wassers bildet, noch groͤßer wuͤrde, so wuͤrde das
Maximum von Geschwindigkeit, welche diese Ebene erlangen koͤnnte, kleiner;
diese Geschwindigkeit waͤre endlich Null, wenn der Winkel ABd gleich zwei rechten Winkeln wuͤrde,
oder was dasselbe ist, wenn die Ebene BD in der
Verlaͤngerung von AB waͤre.
Waͤre hingegen die Ebene zur Linken um BD
geneigt und wuͤrde die Lage Bd' annehmen,
so daß sie mit AB einen Winkel macht, der kleiner
ist als ABD, so wuͤrde die bewegliche Ebene
BD' das Maximum von Geschwindigkeit d'D' waͤhrend der Zeit zu erreichen suchen,
wo ein Wassermolecul die Linie BD
durchlaͤuft. Dieses Maximum waͤre also um DD' groͤßer als Dd'.
Es wird noch groͤßer, wenn man die Ebene so richtet, daß der Winkel ABd' kleiner wird; und endlich wuͤrde
dieses Maximum unendlich groß, wenn man, waͤhrend die Richtung AB dieselbe bleibt, der Entfernung Dd' des aͤußersten Endes der beweglichen
Ebene vom Punkte D, so wie der Ebene selbst, eine
unendliche Laͤnge geben wuͤrde, vorausgesezt jedoch, daß man immer von
allem Widerstaͤnde abstrahirt.
4) Durch Veraͤnderung der Neigung der beweglichen Ebene in Bezug auf die
Richtung ihrer Bewegung muͤßte es also nach der Theorie moͤglich seyn
vermittelst eines fluͤssigen Fadens oder duͤnnen Strahls, der eine
endliche Geschwindigkeit besizt, dieser Ebene nach Belieben eine unendlich kleine
oder unendlich große Geschwindigkeit zu ertheilen. Und dieses ist eine der
Bedingungen, welche man durch das sogenannte Kreiselrad erfuͤllen zu
koͤnnen glaubte.
5) Wir haben aber gesehen, daß man, um von einem Wasserfall alle Kraft zu erlangen,
die er besizt, ihn ohne Stoß in dem Apparate auffangen
und ohne Geschwindigkeit aus demselben austreten lassen muß.
Bei den verschiedenen Hypothesen, welche wir bisher aufgestellt haben, koͤnnte
jedoch keine von diesen beiden Bedingungen Statt finden; denn bekanntlich
muͤßte, um erstere zu erfuͤllen, die Ebene BD zur Richtung die Resultante der Geschwindigkeit
der Fluͤssigkeit und derjenigen der beweglichen Ebene haben, und der zweiten
koͤnnte man nur dadurch Genuͤge leisten, daß man derselben Ebene eine
Richtung geben wuͤrde, welche mit derjenigen der Bewegung einen Winkel gleich
Null macht. Dieselbe auf der Ebene verzeichnete Linie muͤßte also zu gleicher
Zeit zwei verschiedene Richtungen haben, was unmoͤglich ist.
Bei der Annahme einer Ebene BD
wuͤrde also immer der Fall eintreten, daß das Wasser nicht auf sie
wirken wuͤrde, ohne sie zu stoßen, oder daß es sie mit einer gewissen
absoluten Geschwindigkeit verließe, oder auch daß beide nachteilige Umstaͤnde
zu gleicher Zeit Statt faͤnden, abgesehen von den uͤbrigen
Stoͤrungen, welche durch den Stoß verursacht werden.
Da sich die Ersparung an Triebkraft offenbar nicht mit der so eben besprochenen
Anordnung vertraͤgt, so muß die Annahme von geraden Schaufeln ganz aus dem
fraglichen Systeme verbannt werden.
6) Bekanntlich kann man, wenn von der Reibung abstrahirt wird, vermittelst einer
continuirlichen Curve die Richtung der Bewegung des Wassers aͤndern und es
sogar eine entgegengesezte Richtung annehmen machen, ohne daß feine
anfaͤngliche Geschwindigkeit geaͤndert wird und ohne daß man also an
wirklicher Kraft verliert, wenn die verschiedenen Richtungen, welche man dem Gange
des fluͤssigen Strahls ertheilt, alle in derselben horizontalen Ebene sind.
Man muß also, um die Wirkung des fluͤssigen Strahls aufzufangen, an Statt der
beweglichen Ebene, wovon bisher die Rede war, die krumme Flaͤche BD (Fig. 2. Tab. IV.)
anwenden.
Man weiß, daß wenn BE und BA in Groͤße und Richtung die respectiven
Geschwindigkeiten der (krummen) Flaͤche und des Wassers waͤhrend der
Bewegung vorstellen, in welchem Falle BC die
Resultante dieser beiden Geschwindigkeiten ist, das Wasser die Curve BD nicht stoßen wird, wenn die Tangente dieser
Curve in B mit der Linie BC zusammenfaͤllt. Hinsichtlich der lezten Elemente der Curve am
Punkte D, kann man ihr ohne Schwierigkeit die verlangte
Richtung geben.
7) Wir wollen nun an Statt einen einziges unbestimmten fluͤssigen Strahl zu
betrachten, den Fall annehmen, es befinde sich deren eine Anzahl neben einander, so
daß eine Wassermasse von einer gegebenen Dike entsteht und jeder sey auf der Curve
derselben Dike, die er vorher hatte, nicht merklich comprimirbar, so ist er ihr also
parallel und bildet eine der Oberflaͤche, worauf er gleitet, aͤhnliche
Curve, welche fluͤssige Curve selbst wieder dazu dient, die Wirkung eines
zweiten Strahles fortzupflanzen, der diejenige eines dritten empfaͤngt
u.s.f.
Da Alles sich gleich bleibt, Richtung und Kruͤmmung, und die Wassermolecule
sich folglich in die Form, welche die fluͤssigen Strahlen anzunehmen
genoͤthigt sind, fuͤgen koͤnnen, so ließe sich auf jeden die
Betrachtung anwenden, welche uͤber den ersten angestellt wurde, wenn, in dem
Falle, wo die Curve mit der Richtung der Bewegung bei D
eine Tangente bilden wuͤrde, das Wasser sich frei entwikeln koͤnnte. Da diese
Veraͤnderung aber nicht Statt finden kann, so ist es unumgaͤnglich
noͤthig, um sie zu erleichtern, die Curve so zu construiren, daß ihr leztes
Element mit Dg einen gewissen Winkel macht,
welcher jedoch so klein als moͤglich seyn muß.
8) Wenn man so eine gewisse Anzahl von Schaufeln Herrichten wuͤrde, so
erhielte man eine geradlinige Bewegung, welche so lange dauern wuͤrde, als
sich Curven der Wirkung des Wassers darboͤten; und wenn man, an Statt sie
alle auf derselben geraden Linie anzubringen, sie symmetrisch und in gleichen
Entfernungen auf dem Umfang einer kreisfoͤrmigen Scheibe abcd
,
a'b'c'd
' (Fig. 3) befestigt, die auf
irgend eine Art mit ihrer Achse o verbunden ist, und
innen, nach ha, den fluͤssigen Faden oder
duͤnnen Strahl einfallen laͤßt, so erhaͤlt man ein Rad, welchem
das Wasser eine ununterbrochene kreisfoͤrmige Bewegung mittheilen wird.
In diesem Falle, wie in demjenigen der fortdauernden geradlinigen Bewegung
muͤßte, wenn man nur eine kleine Anzahl fluͤssiger Strahlen anwenden
wuͤrde, ihre Wirkung eine unregelmaͤßige seyn, weil nicht alle
anfangen wuͤrden die Curven am Punkt a zu
druͤken, sondern ein Theil sie erst gegen die Mitte ihrer Laͤnge
erreichen wuͤrde, so daß ein Stoß entstuͤnde, und das Wasser nicht
gehoͤrig benuzt waͤre.
9) Um diesen Uebelstand zu vermeiden, und das Rad in Stand zu sezen, eine große Menge
Wasser aufzunehmen, folglich bei kleinen Dimensionen mehr Kraft zu liefern, ziehe
ich es vor, so viele Wasserstrahlen anzuwenden, als der Umkreis des Rades vertragen
kann, und lasse das Wasser auf alle Curven zu gleicher Zeit wirken, indem ich den
Raum abcd in eine gewisse Anzahl von
Faͤchern vertheile, die durch Fuͤhrer oder
Leiter begraͤnzt sind, welche in der Richtung ha der einfallenden Strahlen angebracht sind. Da sich auf diese Art das
Wasser nach der verlangten Richtung ha
laͤngs der Leitungsfaͤcher bewegt, so behaͤlt es diese
Richtung, wenn es dieselben verlaͤßt, bei, und wirkt dann auf die Curven
unter dem verlangten Winkel.
10) Wenn aber diese Richtung immer und allenthalben denselben Winkel mit den
verschiedenen Halbmessern machen sollte, so muͤssten eben so viele Strahlen
als Halbmesser vorhanden seyn, und folglich eine gleiche Anzahl von Leitern, was
einen ungeheuren Verlust an Raum und eine betraͤchtliche Reibung zur Folge
haͤtte.
Da andererseits die Richtung jedes dieser Leiter mit den beiden anliegenden Leitern
einen gewissen von ihrer Anzahl abhaͤngigen Winkel macht, so streben diese
Leiter, in einer geraden Linie nach ihren respectiven Spuren verlaͤngert,
alle zusammenzutreffen, beengen so den inneren Theil des Raumes, welchen sie
begraͤnzen, und machen wegen der großen Divergenz der Strahlen die
Einfuͤhrung des Wassers in das Rad unter der verlangten Richtung sehr
schwierig, um nicht zu sagen unmoͤglich.
Wenn man die Leiter verlaͤngert, bis sie zusammentreffen, so kann die Speisung
der Faͤcher nur von Oben Statt finden, was durch die kleine freie
Oberflaͤche der Gehaͤuse fast immer unmoͤglich gemacht
waͤre. Wuͤrde man hingegen dem Leiter nur eine kleine Laͤnge
geben, so daß sie nicht zusammentreffen koͤnnen, so faͤnde die
Speisung vom Mittelpunkt zum Umfang in derselben Zeit wie von Oben her Statt.
Da die Leiter alsdann dem seitwaͤrts in die Faͤcher eintretenden Wasser
gerade isolirte Flaͤchen darbieten, so wuͤrde sich die
fluͤssige Ader stark zusammenziehen, und indem sie sich von den Leitern
trennt, die Richtung, die sie haben muß, verlieren.
11) Um dem Wasser diese Richtung so viel als moͤglich zu ertheilen und zu
erhalten, benuzte ich die Eigenschaft der Koͤrper, am lezten Element der
Curve, worauf sie sich bewegen, nach der Tangente zu entweichen; und wende krumme
Scheidewaͤnde b'a (Fig. 4) an, welche, indem
sie sich einerseits gegen das Centrum o richten, und
andererseits mit der verlangten Directionslinie ba
eine Tangente bilden, das Wasser ohne Stoß und ohne die noͤthige Divergenz zu
schnell zu bewirken, in die fluͤssigen Faͤden bis zu den Curven des
Rades leiten.
12) Die allgemeinen Einrichtungen, auf welche wir im Laufe dieser Betrachtungen
gekommen sind, sieht man in Fig. 4 auf Tab. IV.
abgebildet, und wir wollen nun nach Navier die Theorie
des Rades, welches sie liefern, studiren, ehe wir zur Beschreibung der von mir
erbauten Raͤder uͤbergehen. Wir bezeichnen mit:
V die Geschwindigkeit, womit sich das Wasser nach der
Linie ba bewegt.
v die Winkelgeschwindigkeit des Rades.
r die Entfernung irgend eines Punktes des Rades von der
Achse.
r' die Entfernung des Punktes, wobei das Wasser in das
Rad tritt, von der Achse.
r'' die Entfernung des Punktes, wo das Wasser austritt,
von der Achse.
α den Winkel bao, welchen der Wasserstrahl
mit dem Halbmesser bildet.
δ den Winkel lik, welchen das lezte Element
der Curve mit der Tangente am Umkreis des Rades macht.
P die Kraft, welche am Punkt a in der Richtung der Tangente des inneren Umkreises des Rades
ausgeuͤbt wird.
m, E, π, g bezeichnen die Masse, das Volumen, das
Gewicht der Wasservolumeneinheit und die Schwerkraft.
Da die Curven a, i, wie wir vorher gesagt haben, so
angebracht sind, daß sie bei a eine Tangente auf die
Resultante der effektiven Geschwindigkeit des fluͤssigen Strahls im Augenblik
seines Eintrittes in das Rad, und des Punktes a des
Rades bilden, so wird das Wasser diese Curven nicht stoßen; es wird also keine
lebendige Kraft hier Statt finden, und man braucht nur die lebendige Kraft zu
bestimmen, welche das Wasser besizt, wenn es das Rad verlaͤßt.
Die Geschwindigkeit des Wassers, wenn es in das Rad tritt, ist V nach ba; sie entspricht der
Geschwindigkeit da = V
cos. α in der Richtung des Halbmessers, und die Geschwindigkeit bd = V sin. α
ist senkrecht auf diese Richtung oder in der Richtung der Bewegung des Rades.
Die Geschwindigkeit des Punktes a ist vr'.
Die relative Geschwindigkeit, womit das Wasser anfangen wird, laͤngs der Curve
zu laufen, ist also
Textabbildung Bd. 53, S. 249
Die lebendige Kraft, welche das Wasser in diesem Augenblike besizt, wenn man nur
seine relative Bewegung im Rade betrachtet, ist
m ((V sin a – vr')² + V² cos.² α).
Waͤhrend das Wasser im Rade enthalten ist, muß diese lebendige Kraft um das
Doppelte der Wirkungsgroͤße zunehmen, die ihm die Centrifugalkraft ertheilt;
leztere betraͤgt
ʃ mv²dr = 1/2 mv² (r''² – r'²).
Die lebendige Kraft des Wassers muß also werden
m ((V sin. α + vr')² + V² cos.α² + v²(r''² – r'²))
oder
m (V² – 2 vr' sin. α V
+ v² r''.²)
Die effective Geschwindigkeit im Augenblik, wo das Wasser das Rad verlaͤßt,
ist also
Textabbildung Bd. 53, S. 249
Die correspondirende lebendige Kraft, welche das Wasser alsdann besizt, ist gleich
dem Product der angewandten Wassermasse m in das Quadrat
dieser Geschwindigkeit, und folglich gleich
Textabbildung Bd. 53, S. 250
Vergleicht man diese lebendige Kraft doppelt mit der ausgedruͤkten Wirkung,
welche
1/2 mV² – Pvr'
betraͤgt, so erhaͤlt man als Ausdruk der
erlangten Wirkung
Textabbildung Bd. 53, S. 250
13) Um diesen Ausdruk der Wirkungsgroͤße so groß als moͤglich zu
machen, muß man offenbar vorerst cos δ = 1 oder
δ = 0 haben, das heißt, das Wasser muß aus dem Rad in einer auf seinen
Umkreis gezogenen Tangente austreten. Man hat in diesem Falle
Textabbildung Bd. 53, S. 250
Damit ferner die uͤbertragene Wirkung so groß als moͤglich und gleich
derjenigen sey, welche das Gefaͤlle geliefert hat, muß das Wasser, wenn es
aus dem Rade tritt, eine effektive Geschwindigkeit, gleich Null haben; dieß
erhaͤlt man, indem man den Ausdruk, welchen wir fuͤr diese
Geschwindigkeit gefunden haben, gleich Null sezt.
Man hat also, da cos δ = 1
Textabbildung Bd. 53, S. 250
oder
V – 2 vr' sin.
α V + v²r''² = v² r''²; folglich V = 2
vr' sin. α.
vr' ist die Geschwindigkeit des Punktes a des inneren Umkreises; nennt man diese Geschwindigkeit
u, so hat man
Sin. α = V/2u.
Das heißt, der Sinus des Winkels, unter welchem das Wasser in das Rad eintritt, muß
gleich seyn dem Quotient der Geschwindigkeit des Wassers, dividirt durch das
Doppelte der Geschwindigkeit eines Punktes des Umkreises, auf welchem das Wasser in
das Rad eintritt.
Bringt man diesen Werth von sin. α in den Ausdruk
fuͤr die uͤbertragene Geschwindigkeit, so erhaͤlt man
Pvr' = Pu = mV²/2,
oder wenn man mit H die der
Geschwindigkeit V zukommende Hoͤhe bezeichnet,
und sich erinnert, daß V² = 2 gH ist,
Pu = mgH, gleich
der Wirkung, welche das Wasserrad liefert.
Die Theorie zeigt also an, daß wenn der Gleichung
Sin. α = V/2u
Genuͤge geleistet wird, das Rad das Maximum des Effects der Triebkraft
gibt.
14) Dieselbe Theorie, auf die analogen Raͤder der Toulouser sogenannten
Basaclemuͤhlen angewandt, welche Bélidor
Man sehe Bélidor's
Architectura hydraulica oder die Kunst etc., aus
dem Franzoͤsischen uͤbersezt, Augsburg bei Klett 1764, wo die Toulouser
Basaclemuͤhlen im ersten Bande S. 23 beschrieben und auf Tab. V. und
VI. abgebildet sind.A. d. R. beschrieb und Navier untersuchte, liefert
dasselbe Resultat. Nach den Beobachtungen des Hrn. Poncelet an den Muͤhlen der Stadt Metz, welche durch Raͤder
getrieben werden, die denjenigen der Basaclemuͤhlen zu Toulouse (welche man
ebenfalls Kreiselraͤder genannt hat) ganz aͤhnlich sind, ist es
sicher, daß diese Raͤder weit entfernt, dieses Maximum zu erreichen, weniger
leisten als alle anderen bekannten Wasserraͤder, und es ist daher
unumgaͤnglich noͤthig, um denselben Fehler zu vermeiden, die von der
Theorie vorgeschriebenen Bedingungen so genau als moͤglich zu
erfuͤllen. Darauf glaubte ich also meine groͤßte Sorgfalt verwenden zu
muͤssen.
15) Zuerst wollte ich mich durch ein hoͤlzernes Modell des Bodens F (Fig. 4) und der damit
verbundenen Leitungscurven ab', ab' uͤberzeugen, ob das einem gewissen Druk
unterworfene Wasser, wenn es aus diesen Faͤchern tritt, die verlangte
Richtung ba befolgt; ich fand in der That, daß
sich das Wasser sehr gut nach dieser Linie richtete, aber nur in dem Falle, wenn der
obere Theil der Oeffnungen, welcher so zugerundet war, daß die Zusammenziehung des
Strahls vermieden wurde, eine hinreichende Dike darbot.
Wenn hingegen die Oeffnung durch eine duͤnne Wand geschlossen war, befolgte
das Wasser nicht dieselbe Richtung; es trat fast nach den Halbmessern aus, jedoch
mit dem Unterschiede, daß die hohle Seite der Curve diesen Gang ein wenig
aͤnderte, und das Wasser veranlaßte, gegen die concave Curve bloß eine
Zwischenrichtung zwischen der seinigen und derjenigen der benachbarten Halbmesser zu
befolgen.
Was die Curve betrifft, welche die Fluͤssigkeit durch ihren convexen Theil
leitet, so trennte sich das Wasser von derselben gaͤnzlich, und ließ zwischen
dem lezten Strahl eines Faches und dem ersten des anliegenden Faches einen
dreiekigen leeren Raum, dessen Spize am Ende jeder Leitungscurve lag.
Da ich durch diese Beobachtung die Bedingungen kennen lernte, welche erfuͤllt
werden muͤssen, damit das Wasser ganz genau unter der verlangten Richtung in
die horizontale Ebene austritt, so konnte ich auch nach der Theorie die Richtung des
ersten Elements der Curve bestimmen, so daß der Stoß des Wassers bei seinem Eintritt
in das Rad vermieden wurde. Damit es aus demselben ohne Geschwindigkeit austritt,
muß nach der Theorie das lezte Element der Curve eine an dem aͤußeren Umkreis
des Rades gezogene Tangente bilden.
16) Da die Figur der Curve zwischen ihrem ersten und lezten Element
gleichguͤltig ist, so blieb noch zu bestimmen:
1) Die Breite ag der Krone des
Rades.
2) Die Lage i der Curve auf dieser
Krone.
3) Die Anzahl der anzuwendenden Curven.
1. Die Breite der Krone. Sie muß von der Art seyn, daß die
Kruͤmmung der Schaufeln nicht auf einem zu kleinen Halbmesser Statt findet,
und daß das aͤußere Ende dieser Schaufeln dem Wasser eine hinreichende Summe
freier Durchgaͤnge laͤßt, das heißt eine viel groͤßere, als die
Summe der Oeffnungen, durch welche das Wasser entweicht und in das Rad
laͤuft. Ich fand, daß das Verhaͤltniß 0,70 zwischen dem
aͤußeren und inneren Durchmesser, wenn es sich von kleinen Raͤdern
handelt, und das von 0,75 bis 0,83 fuͤr große, den krummen Schaufeln eine
geeignete Kruͤmmung verschafft, ohne sie zu sehr zu verlaͤngern, wobei
es gut ist, wenn die Summe der kuͤrzesten Entfernungen zwischen beiden die
der Austrittsoͤffnungen uͤberschreitet. An diese Verhaͤltnisse
glaubte ich mich halten zu muͤssen, nachdem ich mehrere andere versucht
hatte, und die Erfahrung hat mich gelehrt, daß diese Wahl gute Resultate
liefert.
17) 2. Die Lage des aͤußeren Endes der krummen
Schaufeln. Wir haben gesehen, daß die Lage der Curven von der Breite des
Rades abhaͤngt; nun haben bei dem Verhaͤltniß 0,70 fuͤr die
kleinen Raͤder und dem von 0,83 fuͤr die großen, die Schaufeln, welche
den passendsten Grad von Kruͤmmung und das verlangte Verhaͤltniß
zwischen den Austrittsoͤffnungen des Rades und denjenigen des Schuzbrettes
geben, ihr aͤußeres Ende in einer Entfernung ig vom Punkt, wo die Tangente des ersten Elements der Curve den
aͤußeren Umfang schneidet, gleich 2/5 von gm, der Entfernung der Punkte, wo die Tangente und ihre durch den
Punktgefuͤhrte Senkrechte den aͤußeren Umfang des Rades schneiden. Da
der Punkt i bestimmt ist, und die Theorie vorschreibt,
daß die Curve ai eine auf den Umfang des Rades bei
i gezogene Tangente bilden muß, so muͤßte der
Mittelpunkt des beruͤhrenden Kreises sich unter dem Halbmesser oi befinden; dann wuͤrde aber, wie ich
schon bemerkt habe, die Entwiklung nicht mehr leicht geschehen, obgleich seine
Einfuͤhrung in das Rad durch den inneren Umfang und seine Ausfuͤhrung
durch den aͤußeren Umfang unter allen moͤglichen Mitteln dasjenige
ist, welches fuͤr diese Entwiklung am besten zu passen scheint. Man thut
daher gut, den Winkel bei i, welchen die Curve und die
Tangente am Umfange des Rades bilden, ein wenig zu oͤffnen, und ihm 10,
hoͤchstens 15° zu geben, an Statt 0° wie die Theorie
vorschreibt.
Dadurch wird freilich ein gewisser Theil der lebendigen Kraft des Rades verloren
gehen; da er aber durch den Vortheil einer leichten Entwiklung aufgewogen wird, so
ist dieser Verlust von keinem großen Belang; man kann sich auch davon
uͤberzeugen, wenn man fuͤr verschiedene aͤußerste Faͤlle
folgenden Ausdruk berechnet
Textabbildung Bd. 53, S. 253
welcher die lebendige Kraft gibt, die das Wasser bei seinem
Austritt aus dem Rade mit sich nimmt. Man mag v beliebig
in den Graͤnzen des Moͤglichen abaͤndern, und δ selbst
zu 15° annehmen, so erreicht der Verlust nicht 1/30, der gesammten lebendigen
Kraft, welche das Wasser besaß.
Auf diese Art wird man leicht zwischen den Punkten a und
i, vermittelst eines oder mehrerer
Kreisboͤgen die Curve ai so verzeichnen
koͤnnen, daß sie in a die Resultante der
Geschwindigkeiten des Wassers im inneren Kreise des Rades beruͤhrt, und mit
dem aͤußeren Umkreis einen Winkel unter 15° betraͤgt.
Uebrigens werde ich in der praktischen Anleitung, welche den lezten Theil dieser
Abhandlung bildet, das mechanische Verfahren angeben, welches ich angewandt habe, um
diese Curven so zu verzeichnen, daß man sie gehoͤrig zusammenhangend und
zugerundet erhaͤlt.
18) 3. Was die Anzahl der krummen Schaufeln betrifft, die man dem Rade zu geben hat,
so scheint sie mir von ihrer Hoͤhe abhaͤngen zu muͤssen, und
diese leztere wieder von dem Wasseraufwand, welchen der Durchmesser des Kreiselrades
vertragen kann.
Offenbar muß die horizontale Oberflaͤche aller Faͤcher viel
groͤßer seyn, als die Summe der Austrittsoͤffnungen des Wassers, weil
im entgegengesezten Falle ein wirkliches Zusammenzwaͤngen des Wassers Statt
faͤnde, welches, die vollstaͤndige Speisung dieser Oeffnungen
verhindernd, nicht gestatten wuͤrde, daß aller Druk des oberen Wassers sich
den Theilen mittheilt, welche auf das Rad wirken; es wuͤrden dann schnelle
Veraͤnderungen in der Richtung der Wasserstrahlen auf den Boden, Stoͤße,
kurz eine vollstaͤndige Unordnung in der Bewegung des Wassers Statt
finden.
Je kleiner die Oeffnungen in Bezug auf die Oberflaͤche der Faͤcher
sind, desto langsamer wird natuͤrlich das Wasser in dieselben hinabgelangen,
desto groͤßer wird der Druk, und desto regelmaͤßiger die Bewegung des
Wassers seyn.
Ich mache daher bestaͤndig den Hohlraum der Austrittsoͤffnungen des
Rades viel kleiner als die Oberflaͤche der Faͤcher, oder vielmehr als
diejenige des inneren Kreises des Rades, nach welcher lezteren ich die Hoͤhe
dieser Oeffnungen regulire, so wie auch diejenige der krummen Schaufeln, welche sich
ganz nahe diesen Oeffnungen und denselben gegenuͤber befinden; die
Flaͤche der krummen Schaufeln muß ungefaͤhr gleich groß seyn. Nur muß
man die krummen Schaufeln etwas hoͤher machen, als die groͤßte
Schuzbrettoͤffnung, um sicher zu seyn, daß kein Wasserstrahl entweicht, ohne
seine Wirkung auszuuͤben.
Hienach ist die Anzahl der anzuwendenden krummen Schaufeln, die ich waͤhle,
diejenige, welche zwischen zwei aufeinanderfolgenden Schaufeln einen
kreisfoͤrmigen Raum, beilaͤufig gleich der Hoͤhe der Schaufeln
laͤßt; und fuͤr zwei oder drei krumme Schaufeln hoͤchstens,
nach ihrer mehr oder weniger betraͤchtlichen Entfernung, wende ich eine
Leitungscurve an, so daß die Anzahl der das Wasser im Rade vertheilenden
Faͤcher halb so groß wie die der krummen Schaufeln ist, fuͤr
Raͤder naͤmlich, die deren nur 18 bis 24 haben, und nur ein Drittel
davon, wenn ihre Zahl daruͤber betraͤgt.
19) Zur Breite der Austrittsoͤffnungen des Wassers nehme ich die
kuͤrzeste Entfernung zwischen dem Ende einer Leitungscurve und der
Convexitaͤt der folgenden Curve; das Product dieser Entfernung mit der Anzahl
der krummen Schaufeln gibt die Breite der Ausflußoͤffnungen; wenn die Curven
aus Eisenblech verfertigt sind, so kann diese Breite, da sie nicht viel vom inneren
Durchmesser des Rades d, multiplicirt mit 1,4
verschieden ist, als gleich 1,4 d berechnet werden.
Da die Hoͤhe der Oeffnungen durch e bezeichnet
ist, so erhaͤlt man fuͤr die Flaͤche der
Austrittsoͤffnungen
o = 1,4 de.
Die Oberflaͤche des inneren Kreises des Rades ist
π/4 d² = 0,785 d².
Sie muß nach dem Vorhergehenden wenigstens vier Mal so groß wie die der
Austrittsoͤffnungen seyn.
20) Nennt man nun
F die zu erzeugende Kraft, in Kilogrammen
ausgedruͤkt, welche in der Secunde 1 Meter hoch gehoben werden;
H die Hoͤhe des Gefaͤlles in Metern;
m das Zusammenziehungsverhaͤltniß des
fluͤssigen Strahls;
n das Verhaͤltniß der nuͤzlichen Wirkung
zur aufgewandten Wirkung;
M die in das Rad einzufuͤhrende Wassermenge, in
Kubikmetern ausgedruͤkt;
so hat man
F/(1000 H . n) = M.
Da die Geschwindigkeit des Wassers V = √(2 gH) ist, so muß man haben
M/(m . V) = 1,4 de.
Da ferner die Flaͤche des inneren Kreises des Rades, gleich 0,785 d²,
wenigstens vier Mal so groß wie der Hohlraum der Austrittsoͤffnungen seyn
muß, so erhaͤlt man
0,785 d² = 5,6 de;
woraus sich ergibt
e = 0,14 d.
Um den kleinsten dem Rade zu gebenden inneren Durchmesser d zu bestimmen, hat man
M = 1,4 demV = 0,196
d²mV;
woraus sich ergibt
Textabbildung Bd. 53, S. 255
So ist also der innere Durchmesser des Rades bestimmt. Da sein aͤußerer
Durchmesser bei Raͤdern unter 2 Meter Durchmesser 100/70 seyn muß, und bei
groͤßeren Raͤdern (100/80 oder 100/83) d,
so kann man leicht seinen Werth finden, welchen man uͤbrigens zwischen obigen
Graͤnzen ein wenig wechseln lassen koͤnnte, wenn die Umstaͤnde
es erheischen.
Da das Maximum der Hoͤhe, worauf das Schuzbrett gehoben werden muß, 0,14 d ist, so hat man
Textabbildung Bd. 53, S. 255
Diese Formeln ergaͤnzen mit dem, was vorher uͤber den Werth des Winkels
α, des Winkels δ, die Breite der Radkronen, die Hoͤhe der krummen Schaufeln,
ihre Lage, ihre Anzahl und die Anzahl der Leitungsscheidewaͤnde gesagt wurde,
die Daten, wonach ich meine Kreiselraͤder baute. Ich gehe, nun zur
Beschreibung der im Großen ausgefuͤhrten Raͤder uͤber.
Zweiter Theil. Beschreibung der hydraulischen
Kreisel, welche nach den im ersten Theile enthaltenen Grundsaͤzen im Großen
erbaut wurden.
1. Kreisel, welche im Jahre 1827 an den
Huͤttenwerken zu Pont-sur-l'Ognon, Departement de la Haute-Saône, ausgefuͤhrt
wurden.
21) Dieses Kreiselrad, welches anfangs nur zu einem einfachen Versuche zur
Ermittelung des Nuzeffectes, den ich von einer derlei Vorrichtung erwarten
konnte, bestimmt war, wurde nach einigen mit dem Prony'schen Zaume angestellten Versuchen alsogleich als Triebkraft
einer Saͤgemuͤhle, einer Dreherei und einer starken Muͤhle
angewendet.
Da ich es mit einem reichlichen Wasserstrome, der vielen Veraͤnderungen in
der Hoͤhe des Wasserstandes unterworfen ist, und zugleich nur einen
geringen Fall hat, zu thun hatte, und da ich des Erfolges nicht ganz gewiß war,
so wollte ich das Kreiselrad so dauerhaft, und zugleich aber auch so wohlfeil
als moͤglich bauen.
Ich ließ daher Alles, was zur Erreichung des fraglichen Zwekes nicht
unumgaͤnglich noͤthig war, weg, und aus diesem Grunde bietet
dieses Kreiselrad nichts Besonderes dar, ausgenommen seinen Bau, und die Art und
Weise, auf welche das Wasser ein- und wieder austritt.
Da es sich bloß darum handelte zu bestimmen, unter welchen Umstaͤnden die
Maschine wirken kann, und die Vortheile und Nachtheile, die sich bei der
Anwendung derselben ergeben wuͤrden, zu ermitteln, so dachte ich, es sey
erst nach dem Gelingen des Hauptgegenstandes Zeit an die Nebenumstaͤnde
zu denken. Ich unterließ daher hier die Erbauung des Schuzbrettes, dessen man
sich gewoͤhnlich bedient, um den Verbrauch an Wasser zu erhoͤhen
oder zu vermindern, die Erbauung der Apparate zum Heben und Senken des
Schuzbrettes; kurz ich ließ alle Theile weg, die keinen directen Einfluß auf das
Gelingen der Versuche hatten.
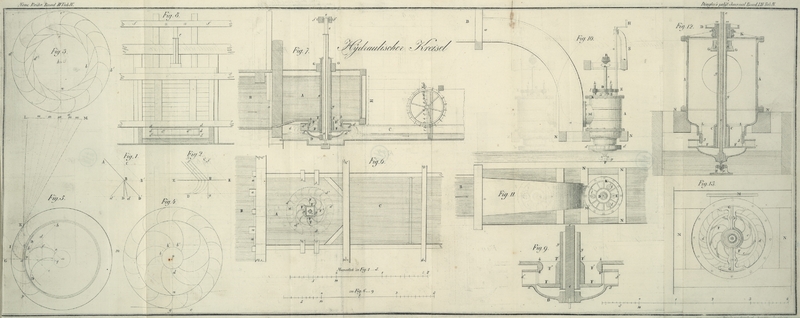
Fig. 6 auf
Tab. IV. ist ein Grundriß des Kreiselrades, wie sich dasselbe zeigt, wenn man es
von Oben von dem Kasten des Aufschlagwassers oder des Wasserbehaͤlters
A sieht, welcher Behaͤlter durch zwei
falsche Schuzbretter a, a nach Belieben mit dem
oberen oder
Ableitungscanale B, der die Triebwerke mit Wasser
speist, communicirt.
Fig. 7 ist
ein Durchschnitt der Maschine nach einer senkrechten, mit der Richtung des
Laufes (coursier) oder Ablaufcanales C parallelen und durch die Achse des Rades gehenden
Flaͤche.
Fig. 8 ist
ein Aufriß des Rades und des hoͤlzernen Wasserbehaͤlters, in einer
gegen die Achse des Ablaufcanales senkrechten Richtung betrachtet.
Fig. 9 ist
ein Durchschnitt des unteren Theiles des hydraulischen Kreisels, in einem
groͤßeren Maßstabe gezeichnet.
An diesen vier Figuren beziehen sich gleiche Buchstaben auch auf gleiche
Gegenstaͤnde.
d ist das Kreiselrad, welches sich unter dem
Wasserkasten oder Behaͤlter befindet; es ist fest an die gußeiserne Welle
e gekeilt, die sich unten in einen
gestaͤhlten Zapfen endigt, welcher sich in einer Anwelle dreht, deren
Grund gleichfalls gestaͤhlt ist. Der obere Theil der Welle dreht sich
zwischen zwei messingenen Anwellen, welche auf eine feste Weise in den beiden
Holzbloͤken f, f, die in die Seitenmauern
eingelassen sind, angebracht sind.
Das Rad, welches aus Gußeisen und ganz aus einem Stuͤke gebaut ist, und an
welchem sich gar keine Vorspruͤnge befinden, die waͤhrend der
Bewegung des Rades im Wasser, Wasser aus der Stelle treiben koͤnnten,
besteht aus einem zum Theil kugelfoͤrmigen oder sphaͤrischen Boden
D, in dessen Mittelpunkt zum Durchgange der
Welle ein Loch angebracht ist. Dieser Boden bildet mit dem umgeschlagenen Rande
oder mit der kreisfoͤrmigen Scheibe d', d'
einen Koͤrper, und an dem Umfange dieser Scheibe, welcher in 18 gleiche
Theile eingetheilt ist, befinden sich eben an diesen Eintheilungsstellen die
krummen Schaufeln d'', d'', d'', d'', auf welche das
Wasser zu wirken hat. Diese Schaufeln, welche senkrecht auf der unteren
vollkommen horizontalen Scheibe angebracht sind, sind mit einer oberen
kreisrunden Scheibe bedekt, die eben so breit ist, wie die untere, und mit
derselben nur durch die krummen Schaufeln in Zusammenhang steht. In der Mitte
dieser Scheibe befindet sich ein ganzer leerer Raum, so daß man den Boden oder
die kreisfoͤrmige Platte F bis etwas
uͤber die untere Scheibe in das Rad einsenken kann, ohne daß er das Rad
auf irgend einer Seite beruͤhrt.
Auf dem kreisrunden und horizontalen Boden F befindet
sich der Kern oder die Nuß F, welcher gleichsam nur
einen Koͤrper mit demselben ausmacht, und der so mit der langen
Roͤhre g verbunden ist, als bestuͤnde
er aus einem Stuͤke mit ihr. Die auf solche Weise an dem Boden F befestigte Roͤhre g steigt senkrecht empor, und wird an ihrem oberen Theile zwischen zwei
Baͤndern GG festgehalten, so daß sie
sich weder drehen, noch auch mit dem Boden F weiter
herabsenken kann, als es erforderlich ist.
Auf der Oberflaͤche des Bodens F und gegen den
Kern F' hin, sind in gleichen Entfernungen von
einander 9 krumme und senkrechte Scheidewaͤnde F'', F'' befestigt, welche das Wasser in die Faͤcher des Rades
fuͤhren, und welche ich Leitungscurven (courbes
conductrices), oder, da sie unbeweglich bleiben muͤssen, auch
fixe Curven (courbes fixes) nenne. Diese Curven sind
in einer Richtung gebogen, welche der Richtung der beweglichen Curven, worunter
ich die krummen Schaufeln d'', d'', die sich mit dem
Rade umdrehen, verstehe, entgegengesezt ist.
Die Scheidewaͤnde oder Leitungscurven steigen bis zu F'', Fig. 7 und 9,
uͤber die obere Scheibe des Rades d, und
uͤber den Boden des Wasserbehaͤlters A
empor. In diesem Boden befindet sich ein kreisrundes Loch, welches zum
Durchgange der Roͤhre g, die ich den
Bodentraͤger (porte-fond) nennen will,
und in der sich die senkrechte Welle e des Rades
frei bewegt, bestimmt ist. Dadurch ist die Communication zwischen dem
Behaͤlter A, den Scheidewaͤnden des
Bodens F und dem zwischen den beiden Scheiben des
Rades befindlichen Raͤume hergestellt.
Die Communication zwischen dem Behaͤlter und dem Boͤden F ist durch eine Art von kleinem Cylinder, dessen
Raͤnder innen abgerundet sind, und der bis auf einige Millimeter unter
die untere Oberflaͤche der oberen an dem Boden befestigten Scheibe
herabsteigt, vermittelt. Die Communication der Scheidewaͤnde oder der
fixen Curven findet durch seitliche Oeffnungen statt, welche von den
Scheidewaͤnden, dem Boden F und der unteren
Seite des kleinen Cylinders b gebildet werden.
Der Gang des Wassers, und die Art und Weise, auf welche dasselbe auf das Rad
wirkt, ist nun folgende.
Wenn die beiden falschen Schuzbretter a, a ganz
gehoben worden, so stuͤrzt das Wasser des Canales B in den Kasten oder Behaͤlter A,
aus welchem es nur durch die mit dem Inneren des Rades communicirenden
seitlichen Oeffnungen entweichen kann. Da diese Oeffnungen jedoch im
Verhaͤltnisse zu den Oeffnungen der Schuzbretter sehr klein sind, und
also nicht alles von den Schuzbrettern gelieferte Wasser verbrauchen
koͤnnen, so folgt hieraus, daß das Wasser in dem Kasten beinahe auf
dieselbe Hoͤhe steigt, die es in dem Canale B
hat. Wenn nun das untere Wasser den Druk der ganzen Wasserhoͤhe H erleidet, so entweicht es seitwaͤrts; da
jedoch saͤmmtliche, den Muͤndungen zustroͤmende Molecule
wegen des Hindernisses, welches sie an den fixen Curven finden, sich nicht in gerader
Linie fortbewegen koͤnnen, so folgen sie diesen Curven bis an ihr Ende,
um dann in der gewuͤnschten Richtung und mit einer Geschwindigkeit von
V = √(2 gH) in das Rad zu gelangen. Das Wasser zwingt mithin, indem es in
Folge dieser Geschwindigkeit auf die beweglichen Curven druͤkt, auf denen
es hingleitet, bevor es am aͤußeren Umfange des Rades austritt, diese
Curven zum Nachgeben, und dreht folglich das Kreiselrad.
22) Man wird bemerken, daß der Cylinder b eine
bedeutende Dike hat, damit der Wasserstrahl nicht contrahirt wird, und damit das
Wasser horizontal austritt, und, bloß von Ruͤkwaͤrts
gedruͤkt, einen gewissen Raum durchlauft, waͤhrend welchem es die
verlangte Richtung annimmt. Ware die obere Wand der Muͤndungen zu
duͤnn, so wuͤrde diese Wirkung nicht Statt finden, und das Wasser
wuͤrde nicht unter dem Winkel a, dessen Werth von der Theorie streng
gefordert wird, in das Rad eintreten.
Bei diesem Baue glaubte ich stehen bleiben zu muͤssen, um die Anwendung
des Principes der Kreiselraͤder im Großen zu versuchen.
Das beschriebene Rad kam auf beilaͤufig 500 Franken zu stehen. Durch
Versuche sollte ermittelt werden, welches die Kraft der Maschine seyn
wuͤrde, und welchen Bruchteil des theoretischen Nuzeffectes des Wassers
sie außer dem Wasser, und auf verschiedene Tiefe getaucht, zu geben im Stande
ist.
Zu diesem Behufe wurde an dem oberen Theile der Welle eine Rolle und ein Zaum
angebracht. Der Hebel des Zaumes, der, um eine bestaͤndig
gleichmaͤßige Laͤnge desselben zu erzielen, mit einem Kreisbogen
versehen war, wurde durch ein Seil, welches uͤber eine Rolle lief, mit
einer Waagschale verbunden, auf welche man die Gewichte, womit das Rad belastet
wurde, legte. Die Vorsichtsmaßregeln, die ich bei der Anwendung des Zaumes jedes
Mal beobachtete, sind im Bulletin de la
Société industrielle de Mulhausen No. 6, S. 14 angegeben.
Hr. Thirria, Bergingenieur, in dessen Gegenwart die
Versuche mit diesem Kreiselrade angestellt wurden, hatte die Guͤte die
Leitung einiger Operationen zu uͤbernehmen.
Die Resultate der drei Versuche, die dem Maximum am naͤchsten kamen,
ergaben, das Rad mochte untergetaucht seyn oder nicht, einen Nuzeffect, welcher
0,83 des theoretischen Kraftaufwandes betrug. Bei den spaͤteren
Versuchen, die gleichfalls in Gegenwart des Hrn. Thirria angestellt wurden, und die im dritten Theile dieser Abhandlung
enthalten sind, war das Verhaͤltniß des Nuzeffectes zum Kraftaufwande
noch groͤßer.
2. Kreiselrad, welches zum Betriebe des Geblaͤses
des Hochofens zu Dampierre (Jura) erbaut
wurde.
23) Dieses Kreiselrad, welches sich an einem von einem Teiche gespeisten
Wasserstrome befindet, arbeitet unter einem Gefaͤlle, das je nach der
Quantitaͤt des in dem Teiche enthaltenen Wassers von 3 bis zu 6 Meter
wechselt. Die Einrichtung desselben, die man aus Fig. 10, 11, 12 und
13
auf Tab. IV. ersieht, unterscheidet sich von jener des eben beschriebenen Rades
nicht bloß durch die Hoͤhe des Gefaͤlles, sondern auch noch durch
das Vorhandenseyn eines regulirenden Schuzbrettes, womit die Kraft der Maschine
erhoͤht oder vermindert wird, je nachdem man eine groͤßere oder
geringere Menge Wasser in dieselbe stroͤmen laͤßt. Dieses Rad
unterscheidet sich ferner von ersterem dadurch, daß das Wasser in einen oben
luftdicht verschlossenen, gußeisernen Cylinder A
geleitet wird, der hier die Stelle des Kastens oder Wasserbehaͤlters,
welcher in Fig.
7 gleichfalls mit A bezeichnet ist,
vertritt, so wie auch noch durch mehrere andere Nebensachen, die spaͤter
angegeben werden sollen.
Fig. 10
ist ein Aufriß des Treibrades, des gußeisernen Cylinders A, unter welchem sich dasselbe befindet, des Mechanismus, der zum
Heben und Senken des kreisrunden Regulirschuzbrettes dient, und unter dem Dekel
des Cylinders angebracht ist, und des kegelfoͤrmigen Getriebes oder
Winkelrades, welches sich an dem oberen Ende der Welle des Rades befindet, und
welches die Bewegung dieser Welle durch ein Winkelrad auf das Geblaͤse
uͤbertraͤgt. Man sieht ferner aus dieser Figur auch den Kasten B mit der hoͤlzernen Roͤhre aa, welche das Wasser aus dem Kasten in den
Cylinder A fuͤhrt, aus welchem es hierauf in
das Rad uͤbergeht.
Fig. 11
ist ein Grundriß der Maschine von Oben gesehen.
Fig. 12
und 13
zeigen in einem doppelt groͤßeren Maßstaͤbe einen Durchschnitt der
Maschine nach einer senkrechten Flaͤche, welche durch die Achse geht, und
auf der Richtung des Ablaufcanales senkrecht steht; und einen Grundriß, in
welchem der Dekel von dem Querholze, wodurch die Bodentragroͤhre fixirt
ist, von den Scheidewaͤnden mit fixen Curven, und von dem unterhalb
befindlichen, durch punktirte Linien angedeuteten Rade abgenommen gedacht
ist.
dd ist der gußeiserne Kreisel, welcher mit 27
gußeisernen krummen Schaufeln, die aus einem Stuͤke mit dem Rade
bestehen, besezt ist; er ist der Form nach dem in Fig. 6 und 7
abgebildeten aͤhnlich.
e, eine Welle aus Schmiedeeisen, die sich mit großem
Spielraume in den senkrecht gegen das Rad gestellten Bodentraͤger
dreht.
F, der kreisrunde Boden mit seinen 9 fixen Curven
und mit dem
Centralkerne CC, durch welchen die den Boden
tragende Roͤhre geht. Der Kern besteht nicht aus einem Stuͤke mit
dieser Roͤhre, sondern ist nur fest an dieselbe gekeilt.
G, ein gußeisernes Querstuͤk, welches in
Einfalzungen, die an dem Cylinder A angebracht sind,
gekeilt ist. Um die Roͤhre g herum, und in
einer cylindrischen, nach Unten mit umgeschlagenen Raͤndern versehenen
Oeffnung, welche in der Mitte des Querstuͤkes G angebracht, und an dem oberen Theile mit einer Ausladung oder
Schulter ausgestattet ist, laͤuft eine gußeiserne Zwinge h, die aus zwei Stuͤken besteht, damit sie um
so leichter an dem Halsringe der Roͤhre g
angebracht werden kann. Diese Ausladung oder Schulter ist es, welche
hauptsaͤchlich zum Tragen der Roͤhre und des Bodens F dient. Da sich die Roͤhre senkrecht in der
Mitte der Maschine befindet, so werden die beiden Theile der Zwinge h, welche die Schulter umfassen, stark in das
Querstuͤk G gekeilt, so daß sich die
Roͤhre und der Boden nicht drehen und nicht in Unordnung gerathen kann.
Dieses Querstuͤk ersezt daher an gegenwaͤrtiger Maschine die
beiden hoͤlzernen Baͤnder G, G, von
denen ich oben bei erster im Kreiselrade gesprochen, und ich will dieses
Querstuͤk daher die Unterlage fuͤr den Bodentraͤger
nennen.
Das Querstuͤk G hat zwei Loͤcher i, durch welche die eisernen Stangen k gehen, die an den oberen Enden mit
Schraubenwindungen versehen sind. Diese Stangen dienen zum Senken und Heben des
kreisrunden Schuzbrettes J, und zwar mittelst der
drei kleinen Getriebe l, l, l, welche den Stangen
k, k als Schraubenmuttern dienen.
D ist ein Zahnrad, welches sich mit gelinder Reibung
an einem an das obere Ende der Roͤhre g
gekeilten Halsringe m dreht. Dieser Halsring, der
mittelst vier Schrauben n, n gegen eine
Fuͤtterung aus Hanf, womit die Roͤhre in einem kleinen, aus der
Mitte des Dekels K emporsteigenden Cylinder umgeben
ist, angedruͤkt wird, wirkt nach Art der Stopfbuͤchsen, und
verhindert, daß der innere Theil des gußeisernen Cylinders A mit dem aͤußeren communicire, und daß
folglich kein Wasser aus demselben entweichen kann.
Das Rad D erhaͤlt seine Bewegung durch einen
Triebstok E, an dessen Welle o eine Kurbel H aufgezogen ist, welche zum
Umdrehen derselben dient. Die den Getrieben l, l
mitgetheilte Bewegung bewirkt, daß sich die Stangen k,
k, und folglich auch das Schuzbrett J, an
welchem sie festgemacht sind, heben oder senken.
K ist der gußeiserne Dekel des Cylinders A, er ist durch Zapfen oder Bolzen befestigt, und
bildet ein solches Gefuͤge damit, daß kein Wasser entweichen kann. Um dem
Dekel mehr Festigkeit zu geben, ist er mit 12 Rippen und am Rande mit einem
hervorragenden Ringe versehen.
L, der Boden, der den Cylinder mit dem Schuzbrette
J vereinigt, und die Leitungscurven des Bodens
F einschließt. Dieses Stuͤk ist nicht
unumgaͤnglich nothwendig; allein es verhindert großen Theils die
Contraction, die sonst bei dem Eintritte des Wassers in die Faͤcher Statt
finden wuͤrde.
M, eine an dem Cylinder angebrachte Tubulirung,
durch welche der Cylinder mit dem Rohre a, a,
welches das Wasser von B nach A heruͤber leitet, in Verbindung steht.
N, N, ein in das Mauerwerk eingelassenes
Gebaͤlk, auf welchem der Behaͤlter A
ruht.
O, ein Halsring, der den oberen Zapfen der Welle e umfaßt, und ihm erlaubt sich in seinen Anwellen
umzudrehen.
P, ein gußeiserner Schuh, in welchem sich die Pfanne
oder Anwelle befindet; er ist so gebaut, daß ein cylindrischer, innen
ausgedrehter Aermel, oder eine Zwinge, welche die Pfanne genau umgibt, diese
leztere hindert sich von dem Mittelpunkte zu entfernen. Um diesen Mittelpunkt
ist der mittelst Richtschrauben gerichtete Aermel oder die Zwinge in den Schuh
gekeilt, ohne jedoch die senkrechte Bewegung desselben zu
beeintraͤchtigen. Der an einer Seite pyramidale Bolzen oder
Schluͤssel p traͤgt also das Rad,
indem er sich in den Schuh einsenkt.
Q ist die Pfanne oder Anwelle, und q der Zapfen des Rades.
Die Welle o der Kurbel H,
die zur Bewegung des kreisrunden Schuzbrettes J
dient, wird von einer gußeisernen Stuͤze getragen.
Das Schuzbrett J, welches an den Raͤndern mit
mehreren Lederstreifen besezt ist, ist abgerundet, und mittelst eines
hoͤlzernen Ringes, der durch Schrauben an dem Gußeisen befestigt ist,
verdikt. Der Zwek hievon wurde (22) angedeutet.
24) Um diese Maschine in Gang zu sezen muß das falsche Schuzbrett, welches sich
am Eingange der hoͤlzernen Roͤhre a, a
befindet, geoͤffnet werden; das Wasser laͤuft naͤmlich dann
laͤngs dieser Roͤhre, fuͤllt den Behaͤlter oder
Cylinder A, und uͤbt auf saͤmmtliche
Theile desselben einen Druk aus, der mit der Hoͤhe des Sturzes im
Verhaͤltnisse steht. Dreht man nun, nachdem diese Vorbereitungen
getroffen, mittelst der Kurbel H das Getrieb E von Rechts nach Links, so wird dadurch das
mittlere Rad D umgedreht, und dieses wird dann
seinerseits, indem es die Getriebe l, l bewegt, die
drei Stangen kk und das Schuzbrett J heben.
Hierauf oͤffnen sich die seitlichen Abflußmuͤndungen, die, wie bei
21 gesagt worden, von den fixen Curven, dem Boden und der unteren Seite des
Schuzbrettes gebildet werden. Das Wasser entweicht also, indem es einen Druk von
der ganzen Hoͤhe der Wassersaͤule erleidet, mit einer
Geschwindigkeit, die der Hoͤhe des Gefaͤlles und der Richtung, die
ihr von den Leitungscurven gegeben werden, entspricht, und stroͤmt dann
durch das Rad, indem es stark auf die krummen Schaufeln druͤkt. Die
Schaufeln nehmen alsobald eine Geschwindigkeit an, welche von dem
Widerstaͤnde, der ihnen geleistet wird, abhaͤngt; und auf diese
Weise erlangt die Welle also die noͤthige Bewegung, die von dem Getriebe
R an das Geblaͤse fortgepflanzt wird.
25) Aus der eben beschriebenen Einrichtung erhellt, daß man mit einem derlei
Kreiselrade jedes Gefalle von beliebiger Hoͤhe benuzen kann, ohne daß die
Welle eine groͤßere Laͤnge zu haben braucht, als eben
noͤthig ist. Man kann folglich die Bewegung in jeder beliebigen
Hoͤhe nehmen, und das Rad an jedem beliebigen Orte einer Fabrik etc.
anbringen. Ein solches Rad laͤßt sich z.B. sehr leicht in der Mitte eines
Saales unterbringen, und wird bei einer Kraft von 8 bis 10 Pferden und bei einem
Gefalle von 4 bis 5 Meter nicht mehr Raum einnehmen, als ein
gewoͤhnlicher Ofen.
26) Man hat bei dem Baue von derlei Maschinen vorzuͤglich darauf zu
achten, daß man der Wasserleitung des oberen Canales oder Behaͤlters B einen Durchmesser gibt, bei welchem sie, ohne
einen zu großen Verlust am Gefalle zu erleiden, jenes Volumen Wasser liefert,
welches die verlangte Kraft erfordert. Da die Formeln fuͤr den Bau dieser
Art von Wasserleitungen in den Tabellen des Hrn. Prony ausfuͤhrlich berechnet sind, so waͤre es
uͤberfluͤssig dieselben hier zu wiederholen. Ich fuͤge nur
noch den Rath bei, die Wasserleitungen immer lieber etwas groͤßer zu
machen, als sie der Berechnung nach seyn sollten, damit die verschiedenen
Substanzen, die sich nach einigen Jahren immer an den Wanden derselben ansezen,
die Bewegung des Wassers nicht auf eine fuͤr den Gang der Maschine
nachtheilige Weise beeintraͤchtigen.
3. Kreiselrad von der Kraft von 50 Dampfpferden, welches
an dem Huͤttenwerke zu Fraisans erbaut wurde.
27) Die in den beiden vorhergehenden Beschreibungen enthaltenen Details werden
dieses Kreiselrad sehr leicht begreifbar machen; ich werde daher jene Theile,
die den bereits beschriebenen Theilen aͤhnlich sind, kurz
uͤbergehen, und mich dafuͤr bei einigen neueren Einrichtungen um
so laͤnger verweilen.
Man sieht dieses Kreiselrad auf Tab. V. in Fig. 1, 2, 3, 4, 5, 6 und 7
abgebildet. Fig.
1 stellt nur die eine Haͤlfte des Rades und des Wasserlaufes
vor, indem die andere Haͤlfte dieser vollkommen aͤhnlich ist.
d ist das Rad mit seinen 36 krummen Schaufeln; es
hat in seinem Grunde, der beinahe wie eine sphaͤrische Muͤze
geformt ist, 6 kreisrunde Loͤcher, welche das Gießen und das Sezen des
Rades erleichtern.
D ist das kreisrunde Schuzbrett mit seinen
hoͤlzernen Besezen, zwischen denen die fixen Curven angebracht sind.
E ist ein innen rein ausgebohrter Cylinder, in
welchem das Schuzbrett spielt, welches, um das Entweichen des Wassers zu
verhindern, mit Leder besezt ist. Dieser Cylinder hat einen breiten
umgeschlagenen Rand, und in diesem Rande befinden sich viele Loͤcher, die
zur Aufnahme der Bolzen bestimmt sind, womit der Cylinder auf eine solche Weise,
daß keine Erschuͤtterung moͤglich ist, an dem Fußboden befestigt
ist.
e, die Welle des Rades; sie ist an ihrem unteren
Ende mit einem Zapfen p ausgestattet, der sich in
einer Pfanne 5 dreht. Diese Pfanne ist in einem gußeisernen Schuhe P angebracht, und kann mit Huͤlfe des
eisernen Querstuͤkes 7, des Schwengels 9 und der Kette 12, welche auf den
Cylinder 13 aufgewunden wird, gehoben oder gesenkt werden.
F, der Boden mit den 12 fixen Curven, welche das
Wasser in dem Rade unter dem gehoͤrigen Winkel leiten.
f, ein gußeiserner Halsring, in welchem der obere
Zapfen der Welle mittelst zweier Pfannen oder Anwellen an Ort und Stelle
erhalten wird. Man sieht diesen Halsring in Fig. 7 einzeln
fuͤr sich im Grundrisse abgebildet.
g ist die Roͤhre, welche den Boden
traͤgt.
G, die Unterlage der Roͤhre g; sie ist in Fig. 6 mit der aus
zwei Stuͤken bestehenden Zwinge, die die Roͤhre g zuruͤkhaͤlt, abgebildet.
i, i, i, drei eiserne Stangen, welche zum Heben des
Schuzbrettes D dienen; sie endigen sich oben in
Schrauben, welche durch Schraubenmuttern gehen, die an den Mittelpunkt der drei
Raͤder i', i', i' gekeilt sind. Diese drei
Raͤder greifen in das Centralrad C, welches
sich mit gelinder Reibung an dem gußeisernen Halsringe 14 dreht, der im
Mittelpunkte der Maschine an das obere Ende der Roͤhre g gekeilt ist.
Jede der drei Schrauben an den Eisenstangen i, i, i
hat einen kleinen Hut, der, wenn das kreisrunde Schuzbrett geschlossen ist, die
Schraubenmutter
bedekt, und der das Abgehen der Raͤder i', i',
i' hindert, wenn man die Kurbel der Schrauben allenfalls laͤnger
fort drehen wollte, als noͤthig ist.
I, ein Getrieb, welches an der senkrechten Welle h, die das obere Winkelrad k fuͤhrt, aufgezogen ist. Dieses Getrieb bewegt, wenn es sich
dreht, auch das Centralrad C, welches die drei
Raͤder i', i', i', von denen jedes, wie
gesagt worden, mit einer Schraubenmutter versehen ist, in Bewegung sezt; und da
sich nun diese Schraubenmuttern mit den Raͤdern i', i', i' drehen, so muͤssen sich die Stangen i, i, i gleichfalls heben oder senken, so daß auf
diese Weise das Spiel des Schuzbrettes hervorgebracht wird.
Die Raͤder i', i', i', oder vielmehr die daran
befestigten Schraubenmuttern ruhen auf drei kleinen Walzen a, welche in einer gußeisernen Fassung (monture) c angebracht
sind, so daß also durch diese Einrichtung die zum Bewegen des Schuzbrettes
erforderliche Kraft bedeutend vermindert wird.
m, eine an der horizontalen Welle n aufgezogene Kurbel; an derselben Welle befindet
sich auch ein kleines Winkelrad r, welches in das
horizontale Winkelrad k eingreift. Dreht man daher
die Kurbel, so wird das Schuzbrett gehoben oder gesenkt, und auf diese Weise
erhaͤlt man die Kraft, die man noͤthig hat.
N, der Boden des Wasserkastens, unter welchem das
Kreiselrad angebracht ist. In diesem Boden befindet sich ein kreisrundes Loch,
durch welches der Cylinder E, das Schuzbrett D etc. gehen. Durch dieses Loch communicirt das von
Oben kommende Wasser mit der Platte F, an der sich
die fixen Curven befinden, um sich dann von hier aus in das Rad zu begeben.
Der Boden N ist horizontal rings um das
kreisfoͤrmige Loch, von welchem oben die Rede war, gegen die Schwelle des
Schuzbrettes (durch welches, wenn es noͤthig ist, das Einstroͤmen
des Wassers aus dem Doubs durch den gewoͤlbten Canal B in den Kasten des Kreiselrades verhindert wird)
schief geneigt, damit er mit dieser Schwelle, die fuͤr die
hoͤlzernen, nun aufgegebenen Raͤder erbaut worden,
zusammenpasse.
M, Mauern aus behauenen Quadersteinen, die das Beken
des Kreiselrades umgeben, und welche zugleich auch einen Theil des
Gemaͤuers des Gebaͤudes, in welchem sich das Rad befindet,
ausmachen.
Q, ein Lettendamm, welcher zum Theil aus
geschlagenem Mergel, zum Theil aus Steinmoͤrtel besteht, und womit der
Raum, der sich zwischen der Mauer am Eingange des Wassers und der kreisrunden
Einfassung des Bekens des Rades befindet, ausgefuͤllt ist.
U, Gebaͤlk der oberen Schuzbretter.
V, unteres Schuzbrett. V' eine Fuge in den beiden Seitenmauern, in welchen sich dieses
Schuzbrett bewegt. Wenn sowohl dieses Schuzbrett, als jenes am Eingange des
Wassers U geschlossen ist, kann das Beken des
Kreiselrades troken gelegt werden, damit man die allenfalls noͤthigen
Ausbesserungen vornehmen kann. Mittelst dieses Schuzbrettes kann man das
Kreiselrad auch so tief tauchen, als man will, und es auf diese Weise gegen die
Froͤste schuͤzen, denen es uͤbrigens auch ohne diese
Vorsicht nur wenig ausgesezt ist, indem das Beken leicht geschlossen werden
kann.
X, Gebaͤlk, auf welchem die Unterlage der
Roͤhre, die den Boden traͤgt, ruht.
Z, Gebaͤlk, auf welchem das Geblaͤse
und sein Mechanismus, so wie der Fußboden des Gebaͤudes angebracht
ist.
x, Saͤulen oder Pfosten des Gebaͤlkes
der Luftcylinder.
S, gußeisernes, auf den Pfosten x befestigtes Gebaͤlk, in welchem die Zapfen
der eisernen Wellen n und h, an denen sich die Winkelraͤder k
und r befinden, ruhen.
Y, ein Winkelgetrieb, welches durch ein
groͤßeres Winkelrad die Bewegung des Rades an den Mechanismus des
Geblaͤses uͤbertraͤgt.
28) Das Kreiselrad zu Fraisans, welches in Fig. 1, 2 und 3 im
Grundrisse, Durchschnitte und Aufrisse abgebildet ist, ist aus Eisen gegossen;
seine 36 krummen Schaufeln bestehen jedoch nicht aus einem Stuͤke mit den
Scheiben und dem sphaͤrischen Boden, sondern sie sind aus starkem
Eisenblech gebaut, und durch Zapfen und Schraubenmuttern an hervorstehenden
Raͤndern befestigt, die zu diesem Behufe an den beiden Scheiben
angebracht sind. Der Boden F wurde auf gleiche Weise
gebaut, und die fixen Curven, die er fuͤhrt, sind gleichfalls mittelst
Bolzen und Schraubenmuttern daran befestigt.
Die Zusammenfuͤgung und Verbindung der Theile mittelst Bolzen und
Schraubenmuttern mit hervorragenden Koͤpfen ist bei Raͤdern dieser
Art, bei welchen das Wasser, indem es waͤhrend des Fortgleitens wirkt, in
seinem Laufe auf kein Hinderniß treffen soll, mangelhaft. Mein Modell hatte
diesen Fehler nicht; allein die Gießer, denen ich die Ausfuͤhrung
anvertraute, und die mich anfangs versicherten, sich nach meinen Angaben richten
zu wollen, zwangen mich nach langem Warten der Vereinigung durch Bolzen, die sie
mir vorschlugen, meine Zustimmung zu geben, indem sie fuͤrchteten, meine
Anordnungen wuͤrden beim Gusse so viele Schwierigkeiten machen, daß
derselbe ganz mißlingen koͤnnte. Die Koͤpfe hatten wenigstens so
gearbeitet seyn sollen, daß sie keine Vorspruͤnge gebildet hatten; allein
auch diese Vorsicht
wurde nicht befolgt. Der Einfluß dieser Unvollkommenheit wird sich bei den
Versuchen mit kleinen Oeffnungen der Schuzbretter zeigen.
29) Das nach den oben angedeuteten Principien gebaute Rad hat in der Mitte ein
cylindrisches Loch o, o, wie man aus Fig. 2 und 4 sieht. An
dem Umfange dieses Loches befinden sich vier Hervorragende Leisten, die von der
oberen Oberflaͤche bis auf eine Entfernung von 0,05 Meter vom unteren
Rande des Loches oder des Rohres des Rades laufen. In dieses Loch oder Rohr paßt
von Unten, und zwar so, daß es einen Koͤrper mit demselben ausmacht, ein
gußeisernes cylindrisches Gehaͤuse 1, 1, welches außen vier Einfalzungen
hat, die mittelst der 4 hervorragenden Leisten das Rad aufnehmen und tragen.
Im Inneren hat das Gehaͤuse 1, 1 ein kegelfoͤrmiges Loch, dessen
breite Basis nach Unten gerichtet ist. Dieses sehr genau ausgedrehte Loch nimmt
eine Zwinge oder einen Ring 2, 2 auf, der nach der Richtung der Achse in zwei
gleiche Theile getheilt, und nach Außen kegelfoͤrmig, wie das Innere des
Gehaͤuses 1, 1, nach Innen hingegen nach der cylindrischen Form der Welle
e des Rades abgedreht ist.
Dieser Einrichtung gemaͤß wird die Welle von der Zwinge oder dem Ringe 2,
2 umfaßt, welcher auf der an dem unteren Theile dieser Welle befindlichen
Randleiste ruht, und selbst wieder in dem an das Rad gekeilten,
kegelfoͤrmigen Gehaͤuse 1, 1 enthalten ist. Die Welle ist daher
vollkommen gerade und in der Mitte fixirt, wenn das Gehaͤuse 1, 1 mit den
gehoͤrigen und bekannten Vorsichtsmaßregeln in das Loch o, o gekeilt worden. Man kann daher hienach das Rad
schnell von der Welle abnehmen, wenn man dasselbe einige Zoll hoch emporhebt,
und die Welle so wie den aus zwei Stuͤken bestehenden Ring, den man in
Folge seiner kegelfoͤrmigen Gestalt leicht nachlassen kann, nach
Abwaͤrts bewegt. Die beiden Theile des Ringes loͤsen sich von der
Welle ab, wo dann das Loch oder das Rohr des kegelfoͤrmigen
Gehaͤuses 1, 1 den Halsring oder die Schulter der Welle durchtreten
laͤßt, so daß man das Rad also auf diese Weise abnehmen kann.
Da saͤmmtliche Theile durch abgerundete Gefuͤge mit einander in
Verbindung stehen, so koͤnnte sich das Rad auch ohne die Welle umdrehen.
Um es daher damit zu verbinden, und um die winkelige Bewegung des einen von
jener der anderen abhaͤngig zu machen, sind, wie man aus Fig. 4 sieht, in den
Gefuͤgen 4 eiserne Zapfen (languettes ou
prisonniers) angebracht, und zwar solcher Maßen, daß in jeden der Theile, die
einander beruͤhren, je die Haͤlfte derselben eingepaßt ist.
Die Verbindung des Bodens F mit der Roͤhre g, welche denselben traͤgt, ist beinahe auf
dieselbe Weise vermittelt; nur fuͤhrt hier der Boden F selbst einen Kegel, der als Gehaͤuse
fuͤr den aus zwei Stuͤken bestehenden Ring 3, 3, Fig. 1, 2 und 5 dient.
Dieser Ring oder diese Zwinge ist in der Mitte erweitert, und beruͤhrt
daher nur an seinen beiden Enden die Roͤhre, welche den Boden
traͤgt. Auch diese Roͤhre ist mit zwei eisernen Zaͤpfchen
ausgestattet, damit sich der Ring oder die Zwinge nicht in Folge der Einwirkung
des Wassers auf die Leitungscurven drehen kann.
Der Ring oder die Zwinge ist in den Kern des Bodens F
gekeilt, und beide werden sie durch zwei Leisten festgehalten, die jede
Winkelbewegung des Bodens an der Roͤhre hindern.
Fig. 5
zeigt den Boden F von Unten, und zwar mit den 12
Rippen F', die demselben groͤßere Festigkeit
geben.
An dem oberen Theile des Kernes und des Ringes oder der Zwinge ist ein
hoͤlzerner Ring 4, 4 befestigt, welcher die Form eines abgerundeten
Wulstes hat, damit die Contraction, welche das Hervorragen dieses Kernes an der
Roͤhre erzeugen wuͤrde, zum Theil vermieden wird.
Die Unterlage G der Roͤhre, die den Boden
traͤgt, ist, wie Fig. 2 und 6 zeigt,
beinahe auf dieselbe Weise, und wie es schon oben (23) bei dem Rade zu Dampierre
angegeben wurde, gebaut; nur wurden auch an diesem Theile des großen
Kreiselrades zur Verhinderung der Umdrehung der Roͤhre g und des Bodens F die
Zaͤpfchen angebracht, waͤhrend an dem kleinen Rade schon das
Anziehen des Ringes oder der Zwinge an dem Halsringe dieser Roͤhre als zu
diesem Zweke hinreichend erkannt wurde.
Unter den neuen Einrichtungen, durch welche sich dieses Rad von den beiden
vorhergehenden unterscheidet, befindet sich auch der Apparat, durch welchen das
Rad gehoben oder gesenkt werden kann, um den Unordnungen, welche allenfalls
durch die Abnuͤzung des Zapfens p der Welle
e entstehen koͤnnten, zu begegnen.
Der Koͤrper des Schuhes P ist bis auf seine
aͤußere Form, welche hier vierekig ist, und bis auf seine
groͤßeren Dimensionen im Inneren dem Schuhe des zweiten Kreiselrades
aͤhnlich. Er enthaͤlt wie jener eine messingene Pfanne 5, deren
Grund gestaͤhlt ist, und in welcher sich der Zapfen p der Welle dreht. Diese außen cylindrisch
abgedrehte Pfanne paßt mit gelinder Reibung in einen ausgedrehten Ring 6, in
welchem sie sich nach der Richtung der Achse des Rades senkrecht auf und
nieder bewegt. Dieser von Außen vierzig geformte Ring ist fest in den Schuh
gekeilt, der selbst wieder fest an den Boden des Laufes gebolzt ist.
Unter der Pfanne befindet sich ein Falz, in welchen ein starkes, horizontales,
eisernes Querstuͤk 7 paßt; dieses Querstuͤk hat einen Zapfen,
welcher mittelst zweier anderer eiserner Stuͤke 8, von denen jedes
senkrecht an einem Schwengel 9 aufgehaͤngt ist, die Pfanne, deren
Umdrehung er verhindert, den Zapfen, und folglich die Welle und das Rad
traͤgt.
Die beiden gußeisernen Schwengel 9, von denen sich der eine zur rechten und der
andere zur linken Seite des Rades befindet, sind an einer gemeinschaftlichen,
eisernen Achse 10 aufgezogen; und diese Achse kann sich auf Pfannen schwingen,
die auf zwei Wangen oder Pfosten, welche mit dem Schuhe P aus einem Stuͤke gegossen wurden, zusammengefuͤgt
sind.
An dem der Achse entgegengesezten Ende sind die Schwaͤngel durch ein
Querstuͤk oder durch einen Bolzen so mit einander verbunden, daß sie sich
weder von einander entfernen, noch auch sich gegenseitig annaͤhern
koͤnnen. Dieses Querstuͤk steht durch einen, mit einem
Vorsteknagel geschlossenen Haken mit zwei Ketten 12 in Verbindung, und diese
Ketten rollen sich auf einen kleinen Cylinder 13 auf, der an seinen Enden mit
einem Sperrrade versehen ist. Je nachdem nun diese Ketten mittelst eines
eisernen Hebels auf- oder abgewunden werden, wird das Rad gehoben oder
gesenkt, so daß dasselbe also auf diese Weise in jeder geeigneten Hoͤhe
gestellt werden kann, gleichwie dieß auch an den Laͤufern der
Mahlmuͤhlen geschieht.
30) Dieses Kreiselrad wird auf dieselbe Weise, wie die beiden vorhergehenden in
Bewegung gesezt. Will man es nicht mehr tauchen, als es von Natur aus getaucht
ist, so oͤffnet man sowohl stromaufwaͤrts als stromabwaͤrts
die Schuzbretter ganz. Der Behaͤlter oder Kasten fuͤllt sich bis
zu der Hoͤhe, welche der Ausfluß dem Wasser zu erreichen gestattet; diese
Hoͤhe ist bei dem gewoͤhnlichen Ausflusse oder Verbrauche von 1,50
bis 2 Meter in der Secunde beinahe jener des Wasserbekens gleich, und
faͤllt bei einem Ausfluͤsse von 5 Kubikmeter in der Secunde nur um
0,05 Meter. Ein solcher Ausfluß ist jedoch nur dann noͤthig, wenn das
Wasser, indem es um mehrere Meter uͤber sein gewoͤhnliches Niveau
steigt, die Hoͤhe des Wasserspiegels uͤber dem Boden des Kastens,
um das Vierfache oder daruͤber steigen macht. Der Canal kann daher unter
diesen Umstaͤnden eine weit groͤßere Menge Wasser abfließen
lassen, ohne daß die
Hoͤhe des Wasserstandes in demselben eine Veraͤnderung
erleidet.
Wenn der Kasten oder Behaͤlter A mit Wasser
gefuͤllt ist, so dreht man die Kurbel m von
Links nach Rechts, um dadurch das Schuzbrett zu heben, und eine Verbindung
zwischen dem oberen und unteren Wassercanale herzustellen. Da das in den
Faͤchern des Bodens F enthaltene Wasser nicht
von einem Niveau zum anderen uͤbergehen kann, ohne auf die Schaufeln zu
wirken, so wird es folglich das Rad in Bewegung sezen, und ihm eine gewisse
Kraft mittheilen, welche mittelst des Getriebes Y
weiter fortgepflanzt werden kann.
Dritter Theil. Versuche, welche mit Prony's Zaum an den hydraulischen Kreiseln angestellt
wurden.
31) Alles bisher uͤber den fraglichen Gegenstand Gesagte waͤre wohl nur
von sehr geringem Interesse, wenn die Resultate der Versuche, die weiter unten
angegeben werden sollen, nicht gezeigt hatten, daß die beschriebene Art von
Raͤdern einen bedeutenden Vorzug vor den gewoͤhnlichen horizontalen
Raͤdern, denen man gleichfalls den Namen Kreiselraͤder beilegte,
voraus hat.
Die ersten Versuche, die mit einem Rade von der neuen Bauart angestellt wurden, sind
durch ein Protokoll, welches der Bergingenieur des Departements de la Haute-Saône daruͤber aufnahm,
bestaͤtigt. Die in diesem Protokolle aufgezeichneten Resultate waren, obschon
sie den fruͤheren Versuchen entsprachen, zu auffallend, als daß ich nicht
begierig seyn mußte, dieselben durch neue und noch sorgfaͤltiger angestellte
Versuche verificirt zu sehen.
Ich ließ daher stromabwaͤrts von dem Rade einen Damm (barage) anbringen, dessen Grath mit der Wasserflaͤche in dem oberen
Canale gleiches Niveau hatte. Etwas stromaufwaͤrts von diesem Damme deutete
ein an der Wand des Laufes (coursier) befestigtes,
graduirtes Wassermaaß die Hoͤhe der Wasserschichte an, die uͤber den
Damm floß, wenn das Kreiselrad in Gang war. (Siehe Fig. 2, Tab. IV.) Zum
Messen der Geschwindigkeit des Wassers wurde in der Mitte der Stroͤmung, und
beilaͤufig 0,04 von der Oberflaͤche entfernt, ein sehr leichtes
Fluͤgelrad, welches sich um sehr feine Zapfen drehte, aufgezogen. Die Achse
des Rades war senkrecht gegen den Lauf gestellt, und befand sich dem Wassermaaße
gegenuͤber. Die Beobachtungen dauerten 2, 3 und 4 Minuten, waͤhrend
welchen die Zahl der
Umdrehungen des Fluͤgelrades, und jene, welche das Kreiselrad innerhalb
derselben Zeit vollbrachte, gezahlt wurden.
An dem Wassermaaße wurde die Hoͤhe, auf der sich das Wasser im kaufe
stromabwaͤrts erhielt, und die Hoͤhe, auf welche es sich in dem
Behaͤlter oder Kasten A stellte, beobachtet. Der
Unterschied zwischen diesen beiden Niveaus gab die Hoͤhe des Sturzes. Die
Belastung des Zaumes, dessen Radius bestaͤndig 1,225 Meter betrug, wurde
abgenommen.
Die Zahl der Umdrehungen getheilt durch die Zahl der Minuten, waͤhrend welcher
die Beobachtungen dauerten, gab die Geschwindigkeit, und zwar in Umdrehungen per Minute ausgedruͤkt. Diese Zahl multiplicirt
mit 3,20 Meter, – ein Umfang, der etwas groͤßer ist, als jener, der
durch die Mitte der Fluͤgel ging, und den wir als denjenigen betrachteten,
den der Mittelpunkt des Stoßes oder Impulses beschrieb, – gab die
Geschwindigkeit des Wassers per Minute. Diese leztere
getheilt durch 60 gab die Geschwindigkeit per Secunde;
da diese Geschwindigkeit, eine Kleinigkeit abgerechnet, bis zum Damme, dessen Grath
sich 0,123 Meter uͤber dem Boden befand, eine und dieselbe war; und da ich an
dem Rade eine kleine durch die Reibung seiner Achse verursachte Verspaͤtung
annehmen wollte, so nahm ich an der von dem Rade angedeuteten Geschwindigkeit keine
Reduction vor, sondern ließ sie als mittlere Geschwindigkeit gelten, – eine
Annahme, die offenbar zu einem kleinen Irrthume zum Nachtheile des Kreiselrades
fuͤhrt.
Die unveraͤnderliche Breite des Canales multiplicirt mit der wandelbaren
Hoͤhe der uͤber den Damm fließenden Wasserschichte, und das auf die
angegebene Weise berechnete Product mit der mittleren Geschwindigkeit gaben das
Volumen, und folglich auch das Gewicht des Wassers, welches das Rad in einer Secunde
verbrauchte. Dieses Gewicht in Kilogrammen genommen und mit der Hoͤhe des
Gefaͤlles multiplicirt, gab die Quantitaͤt der verbrauchten Kraft.
Andererseits ergab sich aber aus der Zahl der Umdrehungen des Kreiselrades und aus
der Belastung des Zaumes der erzeugte Nuzeffect, und dieser leztere getheilt durch
die Quantitaͤt der verbrauchten Kraft gibt das Verhaͤltnis zwischen
diesen beiden Quantitaͤten, – ein Verhaͤltniß, dessen
Ermittelung von Interesse war.
Auf solche Weise wurde folgende Tabelle mehrerer Versuche angefertigt, die im Jahre
1827 mit dem hydraulischen Kreisel zu Pont-sur-l'Orgnon angestellt wurden.
Textabbildung Bd. 53, S. 272
Nummer des Versuches; Gefälle;
Geschwindigkeit des Wassers; Geschwindigkeit des äußeren Umfanges des Rades;
Verhältniß der Geschwindigkeit des Rades zu jener des Wassers; Volumen des per
Secunde verbrauchten Wassers; Quantität der verwendeten Kraft, ausgedrükt in
Kil., die auf 1 Met. per Secunde gehoben wurden; Belastung des Zaumes am Ende
eines Halbmessers von 1,225 Meter; Zahl der Umdrehungen des Rades per Minute;
Nuzeffect, ausgedruͤkt in Kil., die per Sec. auf 1 Met. gehoben wurden;
Verhaͤltniß d. Nuzeffectes zur Quantitaͤt der verwendeten Kraft;
Bei einer Tauchung des Rades von 0,65 Meter; Bei einer Tauchung des Rades von
0,51 Meter; Bei einer Tauchung des Rades von 0,25 bis 0,30 Meter
33) Die erste Bemerkung, die sich bei Betrachtung dieser Versuche aufdringt, wird
wohl die seyn, daß das Rad, es mag getaucht seyn oder nicht, beinahe eine und
dieselbe relative Quantitaͤt Nuzeffect gibt. Nach dem Versuche 12, bei
welchem das Rad nicht getaucht war, betrug der Nuzeffect 0,88 des theoretischen
Krafteffectes. Bei dem Versuche Nr. 23, bei welchem das Rad um 0,51 getaucht war,
betrug der Nuzeffect 0,80, und bei dem Versuche Nr. 26, d.h. bei einer Tauchung von
0,25 bis zu 0,30, betrug er 0,87.
34) Eine zweite Bemerkung wird die seyn, daß, wenn das Gefaͤlle dasselbe und die
Abflußmuͤndung unveraͤndert blieb, der Verbrauch an Wasser mit der
Geschwindigkeit des Kreiselrades abnahm.
Die Hoͤhe des Wassers an dem unteren Wassermaaße wechselte bei allen Versuchen
nicht uͤber 0,02 Meter, und doch machte das Fluͤgelrad, wenn sich das
Kreiselrad ohne Belastung oder beinahe ohne solche drehte, beinahe noch ein Mal so
viel Umdrehungen, als es machte, wenn das Kreiselrad stark belastet war.
Ich will mich jedoch nicht weiter uͤber diese Versuche ausbreiten; die in der
Tabelle aufgefuͤhrten Zahlen zeigen zur Genuͤge, daß das fragliche
Kreiselrad nicht nur in der Luft mit mehr Vortheil arbeitet, als man von irgend
einer anderen Art von Raͤdern erwarten kann; sondern daß, wenn das Kreiselrad
auch dem Widerstaͤnde der Fluͤssigkeit, unter welche es oͤfter
getaucht wird, ausgesezt ist, der groͤßere Nuzeffect, den es gibt, doch nur
im Verhaͤltnisse des Sturzes und des Verbrauches an Wasser abnimmt.
35) Mit dem zweiten von mir erbauten und auf Tab. V.
abgebildeten Kreiselrade wurden keine Versuche mit dem Zaume angestellt; es handelte
sich naͤmlich bei demselben nicht darum, dem Eigenthuͤmer zu beweisen,
wie groß der Nuzeffect im Verhaͤltnisse zur verwendeten Kraft ist, sondern
bloß darum, ihm zu zeigen, daß das neue Rad zur Erzielung desselben Nuzeffectes
weniger Wasser braucht, als die anderen Raͤder, und daß sich dasselbe auch
unter dem Wasser dreht, so daß es also gegen die Wirkungen der Kaͤlte und des
Wechsels des Wasserstandes geschuͤzt ist. Zu diesem Zweke wurde das
Kreiselrad unter dasselbe Gefaͤlle gebracht, unter welchem ein vor einigen
Jahren erbautes Eimerrad arbeitete; mit beiden sollten vergleichsweise die Kolben
eines Geblaͤses mit gehoͤriger Geschwindigkeit in Thaͤtigkeit
gesezt werden. Die Oeffnung des Schuzbrettes wurde so regulirt, daß der Verbrauch an
Wasser in beiden Faͤllen gleich war. Man ließ das Eimerrad einige Zeit gehen,
bis seine Bewegung ganz gleichfoͤrmig geworden, und zaͤhlte dann die
Kolbenstoͤße; hierauf sezte man das Eimerrad außer Thaͤtigkeit,
brachte dafuͤr das Kreiselrad in Gang, und zaͤhlte auch hier nach
Herstellung der Gleichfoͤrmigkeit der Bewegung die Kolbenstoͤße. Die
Resultate, die sich hiebei ergaben, waren folgende.
Bei einer Quantitaͤt Wind, welche uͤber 13 oder 14 Kubikmeter per Minute betrug, verbrauchten beide Raͤder zur
Erreichung desselben Nuzeffectes dieselbe Quantitaͤt Kraftaufwand, indem die
Geschwindigkeit sowohl, als die Oeffnung des Schuzbrettes hier fuͤr das
Kreiselrad zu gering waren. In dem Maaße hingegen, als die Oeffnung des Schuzbrettes
und die Geschwindigkeit groͤßer wurden, gab das Kreiselrad unter uͤbrigens gleichen
Umstaͤnden mehr Wind, als das Eimerrad. Wenn mein Rad endlich unter den
Verhaͤltnissen, fuͤr welche sein Bau berechnet war, arbeitete, so gab
es einen bedeutend groͤßeren Nuzeffect, als das Eimerrad, mit welchem es
verglichen wurde, und welches gut gebaut und in gutem Zustande war. Dieses Rad, an
welchem ein einziger Arm schwerer wiegt, als mein ganzes Kreiselrad, welches nur 80
Kilogrammen schwer ist, kann naͤmlich nur eine Kraft geben, die nicht
uͤber 3/4 der Kraft meines kleinen Rades betraͤgt, wie sich dieß aus
einer Vergleichung des Maximums des Windes ergab, den das eine und das andere Rad
lieferte.
Um die Leichtigkeit, mit der das Kreiselrad unter dem Wasser arbeitete, zu zeigen,
wurde dasselbe um 1,20 Meter getaucht; es fuhr hiebei nicht nur fort die
erforderliche Quantitaͤt Wind zu geben, sondern es drehte auch noch das
Eimerrad, welches ohne Belastung nur mit Muͤhe eine um die Haͤlfte
geringere Geschwindigkeit annahm, obschon dieses Eimerrad, sobald es von dem
Kreiselrade getrieben wurde, von Oben kein Wasser mehr erhielt.
Ich weiß wohl, daß diese Versuche, einzeln fuͤr sich genommen, noch keinen
Beweis der Guͤte der Maschine geben wuͤrden; allein es handelte sich
darum, einen Mann zu uͤberzeugen, der Versuche dieser Art besser zu
beurtheilen wußte, als die Versuche mit einem Zaume, dessen Anwendung ihm nicht
bekannt war. Da ich ihm die Vorzuͤge des Kreiselrades vor den
gewoͤhnlichen Wasserraͤdern auch durch Zahlen zu erweisen suchte, so
schlug ich ihm vor, einige Versuche mit dem Zaume anzustellen; allein er war schon
nach ein Paar Monaten so sehr durch die Erfahrung von diesen Vorzuͤgen
uͤberzeugt, daß er mich ohne weiteres mit dem Baue des großen Kreiselrades zu
Fraisans beauftragte.
Vierter Theil. Praktische Anleitung zum Baue der
hydraulischen Kreiselraͤder fuͤr jeden einzelnen Fall.
Das Programm der Preisaufgabe, in welchem von den Concurrenten die Ausarbeitung einer
Anleitung gefordert wird, nach welcher die Praktiker, die mit dem Baue von
Kreiselraͤdern beauftragt wuͤrden, dieselben zu bauen im Stande
waͤren, wollte diese Verbindlichkeit der Concurrenten gewiß nicht so weit
ausgedehnt wissen, und von denselben ein langes und ausfuͤhrliches,
saͤmmtliche auf den Bau der Wasserraͤder im Allgemeinen bezuͤgliche Details
umfassendes Werk fordern. Es ist dieß um so weniger denkbar, als diese Aufgabe schon
von mehreren Schriftstellern viel besser geloͤst wurde, als sich dieß von der
bei weitem groͤßeren Mehrzahl der Concurrenten erwarten ließ. Ich glaube
daher dem Sinne des Programmes nicht zuwider zu verfahren, wenn ich jene, die dieses
Werk nicht schon ohnedieß studirt haben, in Betreff der vorlaͤufigen
Operationen auf die Abhandlung des Hrn. Poncelet
uͤber die Raͤder mit krummen Schaufeln verweise,Man findet diese Abhandlung im Bulletin de la
Société d'encouragement 1825. S. 335. A. d. O., und
im Polyt. Journal Bd. XIX. S.
417.A. d. R. und gleich zur Berechnung der Dimensionen und zur Verzeichnung des Rades
uͤbergehe.
Ich seze also voraus, man kenne in Pferdekraͤften ausgedruͤkt die
Kraft, welche man mit einem Kreiselrade, welches bei einem gegebenen Gefalle zu
erbauen ist, erzielen will. Von dieser Voraussezung ausgegangen Verwandelt man diese
Kraft in Kubikmeter Wasser, welche gedacht werden, als wuͤrden sie per Secunde auf einen Meter gehoben, indem man die Zahl
der Dampfpferde, multiplicirt mit der Anzahl Kilogrammen, die man als den Ausdruk
der Kraft eines Pferdes per Secunde auf einen Meter
gehoben annimmt, durch den tausendfachen Betrag der Hoͤhe des
Gefaͤlles in Metern ausgedruͤkt, theilt. Der Quotient, den man auf
diese Weise erhaͤlt, druͤkt dann die Zahl der Kubikmeter Wasser aus,
welche das Rad verbrauchen muͤßte, wenn es das Maximum des Krafteffectes
hervorbringen wuͤrde. Da jedoch der Nuzeffect zwischen 0,70 und 0,83
wechselt, so ist es besser, wenn man 0,70 als das Verhaͤltnis des Nuzeffectes
zu der Quantitaͤt der zu verwendenden Kraft annimmt.
Um daher die Zahl der zu verwendenden Kubikmeter zu erhalten, muß man die oben
gefundene Zahl durch 0,70 dividiren. Der Quotient gibt dann den gesuchten Verbrauch
in Kubikmetern an; dieser Verbrauch muß aber jedes Mal, so oft das Schuzbrett nicht
hoͤher, als auf 2/3 seiner Hoͤhe gehoben wird, dem Producte der
Muͤndung oder Oeffnung des kreisrunden Schuzbrettes mit der durch die
Hoͤhe des Gefaͤlles erzeugten GeschwindigkeitDie Geschwindigkeiten bei verschiedenen Hoͤhen des Gefaͤlles
findet man in dem angefuͤhrten Werke des Hrn. Poncelet, in Bélidor's
Architecture hydraulique mit den Noten des Hrn.
Navier, in dem Werke des Hrn. de Prony etc. berechnet. Sie sind
uͤbrigens der Quadratwurzel des Produktes des Gefaͤlles in
Metern mit der Zahl 19,62 gleich.A. d. O. und mit dem Coefficienten der Contraction, den ich als 0,83 annehme,
gleichkommen Da sich
aber der Verbrauch vermindert (34), wenn die Bewegung des Kreiselrades langsamer
wird, und wenn die Hoͤhe der Muͤndung des Schuzbrettes so groß wie
jene des Rades ist, so muß der Coëfficient 0,83 auf 0,60 reducirt werden, um
ein Rad zu bekommen, welches das verlangte Volumen zu verwenden im Stande ist.
Wenn man nun den oben gefundenen Verbrauch in Kubikmetern durch 0,60 der
Geschwindigkeit des Wassers theilt, so erhaͤlt man den Flaͤchenraum
der Abflußmuͤndung gleich 0. Und da die Hoͤhe e dieser Muͤndung 0,14 von dem Durchmesser des Rades (20) betragen
muß, so erhaͤlt man:
0,14 d² = 0; so daß also d = √(0/0,14).
Es gilt daher als Regel, daß der Flaͤchenraum der Muͤndung, welcher auf
die angegebene Weise bestimmt worden, durch den Bruch 0,14 zu theilen ist, und daß
die Quadratwurzel des Quotienten den gesuchten Durchmesser gibt.
Gesezt z.B. man habe bei einem Gefaͤlle von 2 Metern einen hydraulischen
Kreisel von 30 Dampfpferden (die Kraft eines jeden zu 73,69 Kilogr., die per Secunde auf einen Meter gehoben werden, angenommen)
zu erbauen; wie groß muß da der Durchmesser des Rades seyn?
30 Pferde, jedes zu 73,69 Kilogr., sind gleich: 30 × 73,69 = 2210,7 Kilogr.,
die auf einen Meter gehoben werden. Theilt man diese Zahl durch die tausendmalige
Hoͤhe des Gefaͤlles von 2 Metern oder durch die Zahl 2000, so
erhaͤlt man als die Quantitaͤt der zu erzeugenden Kraft:
2210,7/2000 = 1,105 Kubikmeter;
und da der Nuzeffect nur 0,7 von der Quantitaͤt der
verwendeten Kraft betraͤgt, so erhaͤlt man als wirklichen, von dem
Rade zu bewerkstelligenden Verbrauche:
1,105 Met./0,70 = Kubikmeter.
Die Geschwindigkeit des Wassers bei einem Gefaͤlle von 2 Meter betraͤgt
der Theorie nach: 6,27 Met. = √(19,62 × 2).
Der Verbrauch 1,58 Met. getheilt durch
0,60 × 6,27 Meter = 3,762
gibt die Abflußmuͤndung als:
0 = 1,58/3,762 = 0,42 Meter.
Um den inneren Durchmesser, welcher dem Rade gegeben werden soll, zu finden, mußte
man, wie gezeigt wurde, die Quadratwurzel des Quotienten nehmen: 0,42 Meter/0,14 =
3.
Vollbringt man diese Operation, so erhaͤlt man als inneren Durchmesser d = 1,73 Meter. Dieser Durchmesser multiplicirt mit
einem mittleren Durchschnitte 100/75, zwischen 100/70 fuͤr die kleinen, und
100/85 fuͤr die großen Raͤder, gibt als aͤußeren Durchmesser
des Rades: D = 1,25 × 1,73 Meter = 2,16
Meter.
Hienach waͤre also der innere Durchmesser = 1,73 Meter; der aͤußere =
2,16 Meter. Die Hoͤhe der Oeffnung des Schuzbrettes, welche = 0,14 d ist, waͤre: 0,14 × 1,73 = 1,242
Meter.
Da die Geschwindigkeit des Rades wechseln kann (13), ohne daß dasselbe das Maximum
des Nuzeffectes zu geben aufhoͤrt, wenn man dem Winkel α den durch die
Formel: sin. α = V/2u ausgedruͤkten gibt, so wird man
u = der Geschwindigkeit des Rades oder des inneren
Kreises, wie es der Mechanismus, an welchem das Rad angewendet werden muß,
erfordert, annehmen koͤnnen. Doch darf u nicht
kleiner als 1/2 V gemacht werden, indem, V/(2²V) = 1; der
Winkel α waͤre naͤmlich dann ein rechter Winkel, und diese
Bedingung laͤßt sich nicht erreichen, wenn das Wasser durch den inneren Kreis
eingefuͤhrt wird. Damit der Winkel α so groß als moͤglich, und
die Einleitung des Wassers nicht beeintraͤchtigt werde, muß die
Geschwindigkeit des inneren Umkreises wenigstens 0,58 von jener des Wassers
betragen.
In dem fraglichen Falle betraͤgt die Geschwindigkeit des Wassers 6,27 Meter
per Secunde, folglich betraͤgt das Minimum
der Geschwindigkeit, welche man ihm zu geben hat: 6,27 × 0,58 = 3,64
Meter.
Da aber der Umfang des inneren Kreises 3,14 × 1,73 Meter = 5,42 Meter ist, so
wird die geringste Geschwindigkeit, in Umdrehungen per
Minute ausgedruͤkt: (3,64 × 60)/5,42 = 40 Umgaͤngen per Minute seyn.
Das Rad muß also wenigstens 40 Umgaͤnge machen; besser duͤrfte es
jedoch seyn, deren Zahl auf 50 und daruͤber zu bringen.
Die Geschwindigkeit wird naͤmlich dann seyn: (5,42 × 50)/(60 ×
6,27) = 0,72 von der Geschwindigkeit des Wassers.
Man erhaͤlt mithin, diese als Einheit angenommen:
Sin. α = V/2u = 1/1,44 = 0,695,
was man auf den Tabellen 44 Graden entsprechend finden
wird.
Wenn man also hier an irgend einem Maßstabe 0,05 Meter fuͤr einen Meter nimmt,
so haben die inneren und aͤußeren Halbmesser des Rades mit diesen Halbmessern
den inneren und aͤußeren Umfang beschrieben.
Man zieht, Fig.
5., Tab. IV., den Halbmesser oa an den
Punkt a, und macht den Winkel hao den fruͤher gefundenen 44 Graden
gleich. Dann zieht man vom Mittelpunkte o aus die Linie
od, welche mit ao einen Winkel aod = dao bildet. Hierauf zieht man durch den Punkt e, an welchem ad den Umfang
(der den Kern oder die Roͤhre vorstellt, die sich auf der Platte mit den
fixen Curven befindet) durchschneidet, die Linie eb parallel mit ao; dann errichtet man
auf b, dem Punkte, wo sich be und ha durchschneiden, die Senkrechte
bc, und faͤllt von d, der Spize des Dreiekes ado eine Senkrechte auf die Basis ao.
Der Punkt, an welchem diese verlaͤngerte Linie auf bc trifft, wird dann der Mittelpunkt eines
Kreisbogens seyn, der die Kruͤmmung der Scheidewaͤnde gibt, an denen
bloß der Theil bg gerade ist.
Um die Richtung des ersten Elementes der Curve zu erhalten, fuͤhrt man die
Tangente ap auf den inneren Kreis, und
traͤgt auf die Linie ha, welche die
Direktion der Geschwindigkeit des Wassers gibt, eine Laͤnge ah, die 10 Eintheilungen des Maßstabes gleich ist.
Da nun in dem fraglichen Falle die Geschwindigkeit des Rades u 0,72 von V betraͤgt, so traͤgt
man auf ap 7 2/10 dieser Eintheilungen auf.
Durch die Punkte h und p
werden hierauf die Linien hq und pq gefuͤhrt, welche mit ap und ah
parallel laufen, und auf diese Weise erhaͤlt man ein Parallelogramm, dessen
Diagonale qa die gesuchte Richtung oder Direction
ist.
Nachdem diese Richtung gefunden und bis zum aͤußeren Umfange in G verlaͤngert worden, errichtet man auf aG eine Senkrechte aL, welche unbestimmt verlaͤngert wird, und bei K den aͤußeren Umfang des Rades durchschneidet.
Die 2/5 von GK geben (17) die Entfernung zwischen
G und I, dem Ende der
krummen Schaufel, und was die Curve selbst betrifft, so wird sie auf folgende Weise
bestimmt.
Man beschreibt von dem Mittelpunkte K aus, und mit einem
Radius Kl einen Kreisbogen Ii, und verlaͤngert die gerade Linie IK auf eine unbestimmte Laͤnge. Dann theilt man die Zahl irgend
welcher in der Linie ai enthaltener Einheiten (Millimeter z.B.) durch
die Differenz der Einheit und des Bruches, der den Cosinus des Winkels MKL ausdruͤkt, wo dann der Quotient, den
man durch diese Theilung erhaͤlt, die Laͤnge von KM in Millimetern ausdruͤkt. Wenn man
ferner von dem Punkte M aus auf KL die Senkrechte ML zieht, und durch verschiedene Punkte m, m,
m.... dieser Linie eine Menge gerader Linien mK, mK... fuͤhrt, die
saͤmmtlich durch den Punkt K gehen, so wird die
Laͤnge MI, welche nach einander auf diese
Linien aufgetragen wird, eine beliebige Anzahl von Punkten der Kruͤmmung der
Schaufel geben.
Im Großen laͤßt sich diese Zeichnung anfertigen, indem man sich eines in LM fixirten Lineales und eines beweglichen
Lineales bedient, dessen Laͤnge = MI sich auf
ersterem Lineale schiebt, und sich gegen den Punkt I
stemmt. Ein an dem Ende I auf der geraden Linie mK des Beruͤhrungspunktes der beiden
Lineale angebrachter Zeichenstift wird die verlangte Curve verzeichnen.
Auf diese Weise lassen sich also saͤmmtliche wesentliche Theile der Maschine
bestimmen. Was die hoͤlzerne Besezung D betrifft,
welche zur Vermeidung der Contraction der Wasserraͤder oben und unten in Form
eines Quadranten abgerundet ist, so hat man sich in dieser Hinsicht nach dem, was in
meiner Abhandlung schon gesagt worden, und nach den derselben beigefuͤgten
Zeichnungen zu richten.
Ebendieß gilt auch von den Details der verschiedenen Theile der Maschine, und man
wird sich, wenn das Gefaͤlle uͤber 2 Meter betraͤgt,
fuͤr die auf Tab. IV. abgebildete, oder
fuͤr die aus Tab. IV. und V. ersichtliche Einrichtung zu entscheiden haben. Es
bleibt daher hier nur noch die Zahl der Schaufeln und der fixen Curven oder der
sogenannten Leitungscurven zu bestimmen.
Die Zahl der Schaufeln ist diejenige, die dem Quotienten des inneren Umkreises des
Rades (der hier 5,42 Meter betraͤgt), getheilt durch die Hoͤhe e = 0,24 Meter, am naͤchsten kommt. Hienach
ergibt sich: 5,42/0,24 = 22, als die Zahl der krummen Schaufeln al des fraglichen Rades.
Da diese Zahl zwischen 18 und 24 steht, so muß die Zahl der Leitungscurven (18) die
Haͤlfte von 22 oder 11 betragen.
––––––––––
(Der in vorstehender Abhandlung mehrmals angefuͤhrte Prony'sche Zaum, um die Kraft der Maschinen, die sich
drehen, zu messen, ist in Bd. VIII. S. 431
des Polyt. Journals beschrieben und auf Tab. VII.
das. abgebildet. Eine Verbesserung desselben von dem verdienstvollen Dr. Ernst Alban ist in Bd. XXX. S. 321 enthalten und auf Tab. VII. das. abgebildet. A. d. R.)