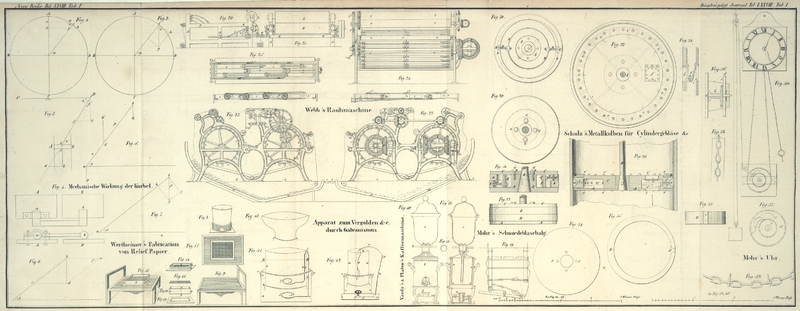
| Titel: | Ueber die mechanische Wirkung der Kurbel; mit Berüksichtigung der über diesen Gegenstand von den HHrn. Russel und Neukrantz erschienenen Abhandlungen. |
| Fundstelle: | Band 78, Jahrgang 1840, Nr. II., S. 5 |
| Download: | XML |
II.
Ueber die mechanische Wirkung der Kurbel; mit
Beruͤksichtigung der uͤber diesen Gegenstand von den HHrn. Russel und Neukrantz erschienenen
Abhandlungen.
Mit Figuren auf Tab.
I.
Ueber die mechanische Wirkung der Kurbel.
Eine Bearbeitung der mechanischen Wirkung der Kurbel hatte ich bisher für ganz
überflüssig gehalten, besonders seit Hr. Russel diesen
Gegenstand in seiner Abhandlung (Dingler's
polytechnisches Journal Bd. LXVII. S. 332)
– wenn auch ganz populär – auf eine höchst genügende Art bearbeitet
hat. Es erschien jedoch eine etwas vehemente Widerlegung der Ansichten dieses
Gelehrten von Hrn. Neukrantz, aus welcher hervorgeht, daß
da und dort noch manche irrige Ansicht über die Kurbel herrscht; dieselbe verdient
übrigens nur darum näher beleuchtet zu werden, weil durch sie mancher Praktiker, dem
Zeit und Gelegenheit fehlt, sich wissenschaftliche Kenntnisse zu erwerben, und der
daher bloß die Endresultate seiner Forschungen auf Treu und Glauben vom Theoretiker
hinnimmt, auf Irrwege verleitet werden könnte. Dieß, und die hohe Wichtigkeit der
Kurbel als mechanische Vorrichtung, dürften daher die Bekanntmachung nachstehender
Zeilen entschuldigen, wobei freilich wenig anderes zu thun übrig bleibt, als die von
Hrn. Russel in seiner Abhandlung gelehrten Wahrheiten
unter anderer, vielleicht noch etwas einleuchtenderer Form nochmals vorzutragen, und
nebenbei die Irrthümer seines Gegners nachzuweisen.
Wir wollen daher zuvörderst die Wirkung der Kurbel untersuchen; alsdann die
Abhandlung des Hrn. Neukrantz zergliedern, und zum
Schlusse noch einige verwandte Punkte berühren.
Wenige Worte werden genügen nachzuweisen, daß bei der Transmission der Kraft von dem
Kolben zur Kurbel kein, im Wesen der Kurbel selbst, begründeter Verlust daran
stattfinde. Wir nehmen hiebei wie gewöhnlich als Maaß des Effectes das statthabende
Moment, welches durch das
Product aus der Kraft in die Geschwindigkeit ausgedrükt wird.
Es sey ABCD (Fig. 1) der Kreis, welchen
die Warze beschreibt, so wird während der Dauer eines Umlaufes derselben der Kolben
den verticalen Durchmesser AC dieses Kreises
einmal hin und her beschreiben. Vergleichen wir nun für irgend einen beliebigen
Punkt c des Kreises ABCD, in welchem sich die Kurbelwarze befinden soll, Geschwindigkeit,
Dampfverbrauch und Nuzeffect des Kolbens mit den Werthen der gleichnamigen Größen,
wenn die Warze sich in D befindet.
Es sey die Warze in D, so wird offenbar die
Geschwindigkeit derselben, welche wir als gleichförmig während des ganzen Umlaufes
betrachten können, und jene des Kolbens dieselbe seyn. Befindet sich hingegen die
Warze in c, und denken wir uns um c den unendlich kleinen Bogen acb, so
kann für diesen, eben wegen seiner Kleinheit, die Sehne ab genommen werden. Sezen wir die Geschwindigkeit der Warze = C, welches also auch die Geschwindigkeit des Kolbens
ist, wenn sich die Warze in D befindet, so wird sie die
Streke ab mit eben dieser Geschwindigkeit C zurüklegen, in derselben Zeit aber auch der Kolben um
das Stük de = af
steigen. Nun ist aber ed = af = ab
cos ν und da ν
= n auch ed = ab
cos n. – Da aber die Geschwindigkeiten den in
gleichen Zeiten zurükgelegten Räumen proportional sind, so haben wir, wenn C' die Geschwindigkeit bezeichnet, womit der Kolben den
Raum ed zurüklegt:
C : C'
=
ab
: ed
=
ab
: ab
cos n
=
1
: cos n.
Aber auch der in den einzelnen Zeittheilen bei einer Maschine ohne Expansion
statthabende Dampfverbrauch ist der Geschwindigkeit des Kolbens proportional;
folglich, wenn d und d' die
respective in den Punkten D und c verbrauchten Dampfmengen bezeichnen, hat man
A.
d : d'
= C
: C'
= 1
: cos n.
Seyen endlich k und k' die
vom Kolben in den Punkten D und c nach der Richtung der Kreistangente ausgeübten Kräfte, so ist für den
Punkt D offenbar k gleich
dem vollen Druke des Kolbens. Im Punkte c wird zwar der
vom Kolben ausgeübte Druk gerade eben so groß seyn, wie im Punkte D, allein nur ein Theil k'
desselben nach der Richtung der Tangente wirksam seyn, der andere Theil aber einen
Druk der Kurbelwelle auf ihre Lager bewirken. Es sey (Fig. 2) cg = k, so ist (mit
Hinweglassung einer Erklärung der ohnedieß verständlichen Figur) hc
= k'. – Da ν =
n und hc = gc
cos ν = gc
cos n = k cos n, so erhalten
wir:
B.
k : k'
= gc : hc
= gc : gc
cos n
= 1 : cos n.
Wir fanden aber oben auch:
d : d'
= 1 : cos n, woraus man
erhält:
k : k'
= d : d', das heißt:
Der auf die Kurbelwarze nach der Richtung der Kreistangente
ausgeübte Druk ist dem Dampfverbrauch – was hier identisch mit dem
Kraftverbrauch ist – proportional; da
ferner die Geschwindigkeit der Warze während des ganzen Umlaufes sich gleich bleibt,
so ist dieser Druk auch dem mechanischen Moment an der Kurbelwarze proportional, und folglich sind die Veränderungen dieses mechanischen
Momentes, – welches Moment das Maaß des
Nuzeffectes ist – ebenfalls den Veränderungen
des Dampfverbrauchs während der einzelnen Momente eines Kolbenspieles
proportional; es wird daher die Dampfkraft in jedem Punkte des
Kurbelumlaufes eben so gut benuzt wie im Punkte D, und
es findet also auch durchaus kein Kraftverlust durch Uebertragung der Bewegung von
einem Kolben an eine Kurbel, oder umgekehrt, statt.Hier ist die durch Menschen- oder Thierkraft bewegte Kurbel
ausgenommen, indem lebende Wesen durch Ausübung eines Drukes, auch ohne
Hervorbringung einer Bewegung, ermatten, und der durch Anwendung ihrer Kraft
erzielte Nuzeffect hiedurch verringert wird. Da jedoch dieser Verlust an
Kraft, oder richtiger, an Nuzeffect keineswegs aus mechanischen, sondern aus
physiologischen Ursachen statt hat, so gehört dieser Fall nicht hieher.
Ich kann nicht umhin, hier noch die Bemerkung beizufügen, daß in der praktischen
Mechanik noch manche Vorrichtung zu finden ist, welche der gleiche Vorwurf mit
gleichem Rechte treffen sollte, welchen Hr. Neukrantz der
Kurbel an der Dampfmaschine machen zu müssen glaubt. Betrachten wir z.B. die mit
Wasser gefüllte Zelle eines oberschlächtigen Wasserrades. Befindet sich dieselbe im
Scheitel des Rades, so drükt sie durch ihr Gewicht auf dessen Zapfen, ohne etwas zu
seiner Umdrehung beizutragen, gerade wie es bei den todten Punkten der Kurbel mit
dem Druk des Dampfes auf den Kolben, und des Kolbens auf die Kurbel, der Fall ist.
Entfernt sich die Wasserzelle vom Scheitel, so wird ein um so größerer Theil ihres,
durch die ganze Wirkungszeit gleich bleibenden Gewichtes, der Umdrehung des Rades zu
Gute kommen, sie selbst aber auch um so schneller sinken, je mehr sie sich dem
horizontalen Radhalbmesser nähert, wo ihr ganzes Gewicht zum Umlauf des Rades beiträgt
u.s.f., so daß das oberschlächtige Wasserrad mit einer so vielfachen Kurbel als
identisch betrachtet werden kann, als gefüllte Wasserzellen daran vorhanden sind,
und bei welcher die Kolben, an unendlich langen Stangen angebracht, nur von
einfacher Wirkung sind, und stets nach genau parallelen Richtungen wirken.
Gerade das Gleiche findet auch bei der Dampfmaschine statt, nur daß es die Expansion
des Dampfes ist, welche bei ihr das bewirkt, was beim Wasserrade das Gewicht des
Wassers; und dennoch hat bei lezterem noch Niemand einen Kraftverlust aus dieser
Wirkungsart deduciren wollen.
Wir wollen nun versuchen, Hrn. Neukrantz's Abhandlung zu
durchgehen, und hiebei vorzugsweise jene Punkte berühren, bei denen derselbe
gänzlich im Irrthum befangen ist; es genügt nämlich nur die wichtigern Punkte ins
Auge zu fassen.
Hr. Neukrantz sagt in seiner Abhandlung (polytechn.
Journal Bd. LXXIV. S. 32 Z. 6 unter der
Tabelle): „Man wird nimmermehr durch Multiplication einer wirklichen Kraft
mit einer relativen Geschwindigkeit ein wirkliches Moment erhalten
können.“
Dieß ist falsch; denn eine relative Geschwindigkeit unterscheidet sich nur dadurch
von einer absoluten, daß bei Bestimmung jener, eine andere willkürlich gewählte
Geschwindigkeit als Einheit angenommen wird, während bei Bestimmung einer
sogenannten absoluten Geschwindigkeit eine solche Einheit schon verstanden ist,
gemeiniglich von 1' per Secunde.
Man kann daher ganz wohl durch das Product aus der relativen Geschwindigkeit in die
Kraft ein relatives Moment ausdrüken, welches sich eben so zum absoluten Moment
verhält, wie die relative Geschwindigkeit zur absoluten. So z.B. verhält sich das
Moment zweier Körper von 15 und 25 Pfd. Gewicht, welche sich mit 90 und 120 Fuß
Geschwindigkeit bewegen = 1350 : 3000. Sezt man aber die Geschwindigkeit des ersten
Körpers = 1, so ist die relative Geschwindigkeit des andern = 1 1/3, und daher die
relativen Momente dieser Körper 1 × 15 und 1 1/3 × 25 oder 15 und 33
1/3. Es ist aber
15 : 33 1/3 = 1350 : 3000.
Man kann also vollkommen zur Bestimmung des Werthes relativer Momente die Kraft mit
der relativen Geschwindigkeit multipliciren.
Jede Horizontalzeile der hier angeführten Tabelle des Hrn. Russel – die übrigens wohl hätte etwas deutlicher disponirt werden
können – dient nun, um zu zeigen, daß das Product aus der Geschwindigkeit des
Kolbens in den Druk, den der Dampf auf ihn ausübt, gleich sey dem Producte aus der
Geschwindigkeit der Warze in die nach der Richtung der Kreistangente auf dieselbe
ausgeübte Kraft. So sagt z.B. die zweite Zeile der Tabelle, daß, während der Kolben
den Raum 1 unter dem Druk von 100 Pfd. zurüklegt, wo also sein mechanisches Moment =
100 ist, die Warze den Raum 3,236 mit der Kraft von 30,90 Pfd. beschreibt, wo also
ihr mechanisches Moment – 30,90 × 3,236, also ebenfalls = 100 ist, und
daß folglich, wie wir bereits oben sahen, hiebei kein Kraftverlust statt hat. Aus
dieser Tabelle ist also ersichtlich, daß für gleiche vom Kolben beschriebene Räume
– also auch für gleichen Dampfverbrauch – der Nuzeffeet an der
Kurbelwarze an allen Punkten ihres Umlaufes gleich ist.
Daß übrigens Hrn. Russel's Tabelle ganz
„absurd“ sey, sucht Hr. Neukrantz dadurch zu beweisen (Anmerkung S. 32), daß er aus der lezten
Zeile der angezogenen Tabelle einen „absurden“ Schluß zieht;
hätte er aber diese Tabelle mit Sachkenntniß betrachtet, so müßte ihn der erste Blik
belehrt haben, daß sein ganzer gewichtiger Beweis auf einem offenbaren
Schreib- oder Drukfehler beruht, indem man die Tabelle bloß nach der ohnedem
in die Augen springenden Ordnung fortzusezen braucht, um zu sehen, daß die lezte
Zeile derselben
statt
10 – 10
180
63,138 mittlere
unendlich
heißen soll
10 – 10
180
0,00
unendlich
und darunter zu
stehen koͤmmt
63,138 mittlere
1,57
und daher diese Tabelle in allen ihren Theilen mit Hrn. Russel's Behauptung übereinstimmt, so wie auch mit dem,
was wir bereits über diesen Gegenstand gesagt haben.
Nun kommen wir zu einem schwer zu erklärenden Theile dieser Abhandlung. Hr. Neukrantz spricht hier von
„effectuirtem“ und „bezwektem“
Kraftmoment. Unter ersterem versteht er offenbar das, was gewöhnlich Bewegungsmoment
genannt wird. Da aber der zweiten Momentsorte bisher noch in keinem Werke über
Mechanik gedacht wurde, so wäre es sehr wünschenswerth gewesen, wenn Hr. Neukrantz etwas Näheres darüber mitgetheilt hätte, statt
sich vor der Hand darauf zu beschränken, seinen Beweisen durch Gedankenstriche und
Ausrufungszeichen den gehörigen Nachdruk zu geben.
Lesen wir nun aber S. 32 bis 36 durch, so geht aus allem hervor, insbesondere aber
aus S. 36 Z. 21 bis unten, daß, während die Kraft (hier der Dampf) den Kolben durch
den Weg 1 mit dem Druk 100 wirklich treibt, und die Warze den Weg 1,57 mit der Kraft
63,1 beschreibt, nach Hrn. Neukrantz's Meinung der Kolben
durch dieselbe Kraft
(Dampf) auch den Weg 1,57 mit dem Druke 100 hätte beschreiben können, „und
darin liegt der Irrthum des Hrn. Neukrantz.“
Gesezt also, an einer gewöhnlichen Dampfmaschine lege der Kolben, auf dessen
Querschnitt von 1 Quadratschuh der Druk von 100 Pfd. wirken soll, den Weg von 1
Schuh zurük, so wird der Dampfverbrauch 1 Kubikschuh seyn, und mittelst desselben
die Warze den Raum 1,57 Schuh unter einem Druke von 63,1 Pfd. zurüklegen, also 100
zum Maaß ihres Nuzeffectes haben. Hr. Neukrantz scheint
nun aber zu glauben, derselbe Kubikschuh Dampf hätte die Warze durch 1,57 Schuh
statt mit 63,1 Pfd. mit 100 Pfd. Druk treiben können, wenn kein Achsendruk statt
gehabt hätte. Es hätte also hiebei ein Körper, der mit einem Druk von 100 Pfd. 1
Schuh zurüklegt, einen Widerstand von 100 Pfd. durch 1,57 Schuh bewegt, d.h. mehr
Kraft geäußert, als er selbst hatte, was nicht möglich ist.
Nach Hrn. Neukrantz's Tabelle, bei welcher in Folge eines
Drukfehlers in den 10 lezten Columnen die lezten Zahlen, welche übrigens denen der
ersten Zeilen gleich seyn müssen, weggelassen zu seyn scheinen, wäre z.B. im Punkte
0 der Figur das bezwekte Moment der Kraft = 100, gerade so wie im Punkte 5. Nun ist
aber im Punkte 0 der Dampfverbrauch = 0, im Punkte 5 = 1. Glaubt nun Hr. Neukrantz, daß – wenn kein Achsendruk stattfände
– der Kolben sich im Punkte 0 ohne Vermehrung des Dampfverbrauches, also
überhaupt ohne allen Dampfverbrauch bewegen würde? Ist es nicht aus eben dieser
Tabelle klar, daß in allen Theilen des von der Warze durchlaufenen Kreises
Dampfverbrauch und „effectuirte“ Geschwindigkeit proportional
sind? Man sieht daher, daß an den sogenannten todten Punkten kein Kraftverlust statt
hat, weil keine Bewegung des Kolbens, und folglich auch kein Dampfverbrauch
vorhanden ist. Es befinde sich z.B. an einem solchen todten Punkte zwischen dem
Kolben und dem Cylinderende 1/10 Kubikschuh Dampf von 10 Atmosphären Druk, so wird
er im ersten Momente, wenn man dem Kolben Bewegung gestattet, nicht mehr Nuzeffect
hervorbringen, als wenn dieß erst nach zehn Jahren geschähe (die Condensation des
Dampfes weggedacht, statt dessen etwa comprimirte Luft vorhanden seyn könnte), und
durch den Achsendruk, den hiebei der gespannte Dampf ausübt, ist also auch nicht der
geringste Kraftverlust eingetreten. Ueberhaupt kann eine Aeußerung mechanischen
Momentes nur durch gleichzeitige Bewegung und Druk stattfinden; ist bloß Druk ohne
Bewegung da – wie bei den todten Punkten der Kurbel, und, wenn der Vorgang
analysirt wird, auch in jedem anderen Punkte des Kurbelumlaufes, jene ausgenommen,
wo die Kraft senkrecht auf den Kurbelarm wirkt – so ist überhaupt kein mechanisches Moment vorhanden,
und folglich kann auch kein Verlust daran statthaben.
In Folge alles bisher Gesagten geht nun auch hervor, daß es ebenfalls ganz irrig ist,
wenn Hr. Neukrantz, S. 33, Anmerkung, behauptet, das
Expansionsprincip sey erfunden worden, um dem von ihm vermeintlich nachgewiesenen
Kraftverlust an der Kurbel zu begegnen. Dieses Princip ist im Gegentheil deßhalb bei
den Dampfmaschinen eingeführt worden, um die Expansionskraft, welche die bei einer
bestimmten Stellung des Kolbens im Cylinder vorfindige Dampfmenge so lange äußert,
bis sie auf die Tension der atmosphärischen Luft herabgesunken ist, der Bewegung des
Kolbens durch frühzeitige Absperrung zu Gute kommen zu lassen; denn im
entgegengesezten Falle – wenn nämlich der Dampf nicht vor Beendigung des
Kolbenhubes abgesperrt wird, und sich der Cylinder mit Dampf von der Tension, wie
sie im Kessel statt hat, füllt – bewirkt dessen Expansionskraft nichts, als
eine nuzlose Beschleunigung der Ausströmung aus dem Cylinder.
Nicht minder irrig ist die Angabe des Hrn. Neukrantz, die
mehrfachen Kurbeln, welche überhaupt bei hinreichender Größe des Schwungrades von
wenig Nuzen sind, seyen ebenfalls wegen des angeblichen Kraftverlustes bei den
Dampfmaschinen benuzt worden, da doch bloß leichtere Ueberschreitung der todten
Punkte und größere Gleichförmigkeit der Bewegung ihr Zwek ist.
Wir kommen nun zur Frage, ob durch die schiefe Stellung der Kolbenstange ein
Kraftverlust hervorgebracht werde, was Hr. Neukrantz
– abermals irrig – bejahend beantwortet. Es sey Fig. 3
AB der Kolben, welcher durch die Kraft ab aufwärts getrieben wird. Der Widerstand,
welchen die Kolbenstange äußert, muß natürlich der Kraft ab das Gleichgewicht halten, und ist zu suchen.
Derselbe kann offenbar nur in der Richtung statthaben, welche die beiden Stüzpunkte
der Kolbenstange verbindet. Machen wir daher bd
⊥ ad, so erhalten wir da für jenen Druk, welchem die Kolbenstange durch
die Wirkung ab des Kolbens unterliegt, während
zugleich ein Seitendruk bd erfolgt, welchen die
Cylinderwand auszuhalten hat. Es ist aber
α = 90° – β, folglich ad = ab/sin α = b cosec. α = ab
sec. β und
bd = ab ·
cos α/sin
α = ab cot.
α = ab tang
β.
Sey nun CD der Balancier, so machen wir ef = ad, und α' sezen wir gleich α, so ist eg = ab die denselben bewegende Kraft, fg aber ein Seitendruk, welcher seine Zapfen
trifft.
Man sieht aus diesem, daß durch die schiefe Stellung der Kolbenstange durchaus kein
unmittelbarer Kraftverlust hervorgebracht wird, und daß überhaupt gar keiner
stattfände, wenn es möglich wäre, die Reibung auf 0 zu reduciren.
Dieser Kraftverlust, welcher durch die Reibung entsteht, wird immer sehr gering seyn.
Denn, bezeichnen wir mit m den Reibungscoefficienten
zwischen Kolben und Cylinderwand, mit k = ab die Kraft, womit der Kolben sich nach Aufwärts
zu bewegen strebt, und mit W den Reibungswiderstand, so
ist
W = mk
tang β.
Nun wird aber wohl nie der Werth von m größer als 0,1
seyn, noch der mittlere Werth von β 10 Grad
übersteigen, somit auch stets W < 0,018 k bleiben, und oft auch – da besonders β meist viel kleiner, als zuvor angenommen wurde,
seyn wird – nur 1/10 bis 2/10 dieses Werthes betragen, d.h. ganz
verschwinden. Es versteht sich übrigens von selbst, daß hier nur von jener Reibung
die Rede seyn kann, welche durch die schiefe Lage der Kolbenstange hervorgebracht
wird, keineswegs aber von jener, welche zur Erzielung eines dampfdichten Schlusses
nöthig ist.
Noch weit geringer ist die Reibung an den Zapfen des Balanciers oder der Kurbel, weil
sie hier zum Hebelsarm den Halbmesser eben dieser Zapfen hat, während der Hebelsarm
der überwältigenden Kraft der Länge der Kolbenstange, des Kurbelarmes, oder der
halben Länge des Balanciers gleich ist. Somit kömmt dieser Widerstand noch weniger
in Betracht, als der zuvor erwähnte.
Es wurde oben α' = α gesezt, d.h. die Lage des Balanciers als horizontal angenommen,
und senkrecht auf die Richtung, in welcher sich der Kolben bewegt. Diese Lage tritt
jedoch während eines Kolbenspieles nur zweimal ein, und ist außerdem immer mehr oder
weniger gegen die Kolbenfläche geneigt. Nachdem wir aber oben sahen, daß bei der
Transmission der Kraft vom Kolben an die Kurbel kein Kraftverlust statt hat, so
brauchen wir hier nur darauf aufmerksam zu machen, daß der Balancier nichts anders
als eine Kurbel ist, deren erster Arm länger ist, als der halbe Kolbenhub, und deren
zweiter Arm, an welchem die Last wirkt, statt an einem anderen Punkte der Achse sich
unter der Gestalt eines Zahnrades zu befinden, in der Verlängerung des ersten liegt.
Sie kann daher keinen ganzen Umlauf vollführen, sondern bloß eine oscillirende
Bewegung annehmen; sie unterliegt daher auch denselben Gesezen, welche bei der
gewöhnlichen Kurbel gültig sind, und pflanzt daher auch ohne Kraftverlust das ihr
mitgetheilte Bewegungsmoment fort. Der einzige Unterschied, welcher zwischen dem
Balancier und der Kurbel stattfindet, besteht in scheinbar verschiedener Richtung der
Bewegung, bei gleichbleibenden Werthen des Kraftmomentes.
Es fällt jedoch auch dieser Unterschied weg, wenn man den Bewegungen der Kurbel für
das Auf- und Absteigen des Kolbens verschiedene Zeichen beilegt, wo alsdann
für den Halbkreis ABC (Fig. 1) die, das
Bewegungsmoment der Warze ausdrükende Formel negativ, für den Halbkreis CDA aber positiv seyn, und daher mit der, für den
Balancier bei gleichen Stellungen des Kolbens statthabenden Formel, zusammenfallen
wird.
Hieraus geht hervor, daß Hrn. Neukrantz's Ansicht in
Betreff der Geradeführungsapparate ganz unrichtig ist. Diese werden bei den
Dampfmaschinen keineswegs aus den von diesem Gelehrten vermutheten Ursachen
angebracht, sondern lediglich deßhalb, damit die durch die schiefe Stellung der
Kolbenstange hervorgebrachte Seitenreibung den Cylinder nicht ungleich abnuze, und
dieser hiedurch seine Rundung verliere.
Das Verhältniß der Seitenreibung des Kolbens zu den Geradeführungsapparaten zu
erörtern, würde die Gränzen dieser Abhandlung allzusehr ausdehnen, und gehört auch
nicht mehr hieher. Es genüge daher zu sagen, daß durch diese Vorrichtungen die
Seitenreibung fast auf 0 reducirt werden, durch unzwekmäßige Einrichtung aber auch
über ihren natürlichen Werth gesteigert werden könne; daß ferner bei denselben, je
nach ihrer Construction, die Seitenreibung entweder ganz, oder auch nur zum Theil
den Geradeführungsapparat trifft, und daher der Uebelstand der ungleichen Abnuzung
des Cylinders ganz oder wenigstens zum größten Theil beseitigt wird.
Die in dem erwähnten Falle statthabende dynamische Wirkungsart der Kolbenstange ist
übrigens nahe verwandt mit jener der Kniepresse, worüber man in Poggendorrff's Annalen, neue Reihe, 11ter Bd., Seite 501
eine treffliche Abhandlung von Fechner nachlesen kann.
Sie unterscheidet sich von dieser im Wesentlichen nur dadurch, daß hier der eine
Schenkel der Kniepresse ganz wegfällt, und folglich auch das die Reibung
vermindernde Gelenk; dann daß die Kraft in einer andern Richtung wirkt, als jene
ist, welche Fechner, als zur Erreichung des größten
Nuzeffectes der Kniepresse nöthig, bezeichnet.
Weiter gehend, stoßen wir in Hrn. Neukrantz's Abhandlung
auf die Beschreibung eines Versuches, welcher nach der Absicht dieses Ingenieurs,
seine Ansichten auch physisch beweist.
Er läßt nämlich die Preßplatte einer hydraulischen Presse als Kraft auf eine
Kurbelwarze wirken, und sieht in dem Zerbrechen der Kurbel, bevor die Warze ihren
höchsten Punkt erreicht, einen unwiderstehlichen Beweis seiner Ansicht, welche
„glüklicher Weise“ ohnedem die Theorie auf ihrer Seite hat
(nämlich – wohlverstanden – nach Hrn. Neukrantz's Meinung).
Es sey daher erlaubt, den hiebei statthabenden Vorgang etwas näher zu beleuchten.
Soll A (Fig. 4) die Unterlage
bezeichnen, worauf das Lager des Kurbelzapfens ruht; B
sey die Preßplatte der hydraulischen Presse: so ist nun der Druk zu suchen, den A und B für einen gegebenen
Erhöhungswinkel α der Kurbel erleiden werden.
Es bezeichne also α (Fig. 5) den
Erhebungswinkel der Kurbel, deren Schwerpunkt in S
liege; ihr Gewicht sey = G, ferner aS = o und Sb = p, so wird die
Kurbel ruhen, wenn in a die Kraft P, und in b die Kraft G aufwärts wirkt,
wo P = Gp/(o + p) und
Q = Go/(o + p) nach bekannten Grundsäzen
der Statik seyn muß. Sezen wir nun noch den
Reibungscoefficienten zwischen b und der Preßplatte
(Fig. 4) =
μ, jenen bei α = μ' den Halbmesser des
Zapfens a = r, und die
Kurbellänge = L: so ist die Kraft zu suchen, welche für
den Neigungswinkel α (Fig. 5) der Kurbel nöthig
ist, um dieselbe, senkrecht an der Preßplatte aufwärts wirkend, zu bewegen.
Nennen wir diese Kraft k, so wird sie einmal den
beständigen Druk Go/(o +
p) (I) überwinden müssen.
Sie wird ferner die Reibung an b zu gewältigen haben.
Diese ist nach dem Vorausgegangenen = μk,
und wirkt parallel mit der Preßplatte. Die zur Ueberwindung derselben nöthige Kraft
ist = μk
tang α (II), denn
macht man ba = μk (Fig. 6), und verzeichnet das Parallelogramm abcd, so ist β = α und daher bd = ab
tang α = μk
tang α.
Endlich wird k auch die Reibung am Zapfen a zu überwinden haben, daher der Druk zu bestimmen ist,
welchem derselbe unterliegt. Sezen wir der Kürze wegen die zur Ueberwindung dieser
Reibung an der Preßplatte nöthige Kraft = k'''; sey
ferner μk
tang α = k'' und Go/(o + p) = k', so wird k = k' + k'' + k''' seyn. Die Kraft k' wird
durch Go/(o + p) ganz
aufgehoben, da diese beiden Kräfte entgegengesezt wirken. – Dagegen haben wir
(Fig. 6)
k'' in ba und ad zerlegt, wovon ba die Reibung μk
tang α überwindet, während ad
– nach der
Längenrichtung der Kurbel wirkend – einen Zug auf a ausübt. Wir haben aber:
ad : db = sec. β : tang
β, und da β = α und db = μk
tang α, so erhält man hieraus:
ad = μk sec. α
(A.).
Der Reibungswiderstand an a (Fig. 5) wirkt am Punkte
b senkrecht auf die Längenrichtung der Kurbel. Sey
bf (Fig. 7) dieser Widerstand,
so wird, wenn wir das Parallelogramm bfgh
verzeichnen, bg jene senkrecht aufwärts wirkende
Kraft seyn, welche nöthig ist, bf zu überwinden,
während zugleich der Zug gf auf die Kurbel wirkt.
Da nun nach dem Vorhergehenden bg = k''' gesezt wurde, und β = α, so ist gf = k''' sin α (B), und
daher der Gesammtzug, den k auf a ausübt, gleich (A + B) = μk
sec α + k''' sin
α.
Außer diesem Zug hält a noch den Druk Gp/(o + p) aus, und
daher sollte, streng genommen, für den Gesammtdruk, den a erleidet, die Resultirende der beiden Kräfte Gp/(o + p) und (μk
sec α + k''' sin
α) genommen werden, welche unter einem Winkel von α' + 90° zusammenwirken, und die wir R nennen wollen. Mit Beziehung auf oben erwähnte
Bedeutung von μ', r und L, wäre dann bf = r/L · μ'R und bg = k''' = bf/cos α = (rμ'R)/(L cos α') wo k''' jedoch noch in den Werth von R eingeht. Betrachten wir aber etwas näher die beiden Kräfte, woraus R entsteht, so sehen wir, daß für kleine Werthe von α, und für jene Dimensionen, wie sie Kurbeln
gewöhnlich zu haben Pflegen, μk
sec α + k''' sin
α gegen Gp/(o + p) verschwinden müsse. Denn alsdann ist k
nahe = Go/(o + p),
welches selbst wieder nie sehr von Gp/(o + p) differiren, also sehr klein seyn wird; es ist sec
α nahe = 1, und μ ein kleiner Bruch; eben so ist k'''
nahe an seinem Minimum, und sin α ein kleiner
Bruch. Wir können daher (da die Richtung von R nicht
berüksichtigt zu werden braucht), statt R sezen Gp/(o + p), wo dann
k''' = μ'
· r/(L cos α)
· Gp/(o + p).
Da nun aber μ' sowohl als r/(L cos α) hier kleine Brüche sind,
deren Product unter Voraussezung gewöhnlicher Verhältnisse 1/50 kaum erreichen wird,
und daher auch μ' r/(L cos α)
Gp/(o + p) gegen Go/(o + p) verschwindet, so kann
für kleine Werthe von α, bei der Bestimmung von
k, die Größe k''' ganz
vernachlässigt werden; d.h. bei kleinen Werthen von α ist der an a statthabende
Reibungswiderstand nur von einem Theil des Gewichtes der Kurbel abhängig, und die zu
dessen Ueberwindung an b nöthige Kraft verschwindet
gegen jene, welche erforderlich ist, um den auf b
lastenden Theil des Gewichtes der Kurbel zu überwinden.
Für größere Werthe von α hingegen wachsen k, sec α und sin
α, während Gp/(o + p) immer gleich bleibt.
Insbesondere durch den Factor sec α erhält der
betreffende Ausdruk einen größern Werth, indeß Gp/(o + p)
verhältnißmäßig noch mehr vernachlässigt werden kann. Hieraus geht hervor, daß wir
zur Vereinfachung der Formel, ohne ihrer Schärfe merklich Eintrag zu thun, statt R für alle Werthe von α sezen können μk
sec α + k''' sin
α.
Wir werden übrigens in der Folge sehen, daß wenn es sich nicht um sehr genaue
Bestimmungen handelt, die Reibung an a ganz
vernachlässigt werden kann, wodurch die Formel für k
sehr einfach wird.
Wir hatten also gefunden k''' = (rμ'R)/(L cos α); in Folge des
später Gesagten verwandelt sich diese Gleichung in k'''
= r
μ'/(L cos α)
(μk
sec α + k''' sin
α) und durch Umgestaltung
Textabbildung Bd. 78, S. 15
Summiren wir nun die Werthe I, II und III, so erhalten wir folgende Gleichung:
Textabbildung Bd. 78, S. 15
und hieraus
Textabbildung Bd. 78, S. 16
wenn wir die constante Größe Go/(o + p) wie
früher Q nennen:
Textabbildung Bd. 78, S. 16
woraus wir für jeden Werth von α jenen von k berechnen können.
Betrachten wir das lezte Glied des Nenners, so sehen wir, daß es (wenigstens bei den
gewöhnlichen Werthen von μ, μ', r und L, und bis zu jenen Werthen von α, wo der Nenner = 0 wird) gegen die anderen Werthe unbeträchtlich
ist, und daher vernachlässigt werden kann, wo dann k =
Q/(1 – μ tang
α)
wird. (V)
Aus dieser Formel geht hervor, daß (den Fall abgerechnet, daß μ und μ' = 0 wäre) die Kurbel
nie einen Erhebungswinkel von 90° erreichen könne, da α früher schon einen solchen Werth erlangen wird, wo k = ∞ und die weitere Bewegung der Kurbel
folglich unmöglich ist; ferner, daß die Kurbel brechen muß, noch bevor α diesen Werth erreicht.
Sezen wir, es sey bei Hrn. Neukrantz's Versuch μ = 1/5; μ' =
1/10; r = 1 Zoll; L = 20
Zoll gewesen, so finden wir jenen Werth von α, wo
k = ∞ nach der strengen Formel (IV) = 78° 24,24' und nach der kürzern Formel (V) = 78° 41,40'. Die Kurbel mußte also brechen,
bevor sie diesen Neigungswinkel erreichte, was nahe genug mit Hrn. Neukrantz's Angabe von beiläufig 70°
übereinstimmt, besonders in Anbetracht, daß hier μ,
μ', r und L willkürlich angenommen
wurden, und in der Wirklichkeit mehr oder weniger von den muthmaßlichen Werthen
abweichen werden.
Es geht hieraus hervor, daß dieses Brechen der Kurbel lediglich von der Reibung
abhing, und keineswegs im Wesen der Kurbel selbst begründet ist; daß dieser Versuch
also weder ein Beweis für Hrn. Neukrantz's Ansicht ist,
noch auch, wie er irrig meint, die Theorie für sich habe.
Es muß übrigens noch bemerkt werden, daß Hr. Neukrantz die
Preßplatte als an einer Treibstange wirkend angibt. Da ich indeß nicht weiß, welchen Theil er
unter dieser Benennung verstanden wissen will, so sind mir in dieser Hinsicht die
praktischen Details seines Versuches nicht ganz klar; es ist indeß abzusehen, daß
durch eine solche Abänderung bloß der numerische Werth von μ möglicherweise eine Abänderung erleiden kann.
Ich kann endlich nicht umhin, schließlich noch eines Punktes zu erwähnen, über den
mitunter ganz unrichtige Ansichten herrschen, und der, außer bei den Dampfmaschinen
mit Wechselbewegung, auch noch bei vielen andern Maschinen, besonders bei Pumpen und
Wassersäulenmaschinen seine Anwendung findet.
Bei Bestimmung der Gesammtkraft, welche zur Ausführung eines Kolbenhubes, z.B. bei
einer Wasserpumpe nöthig ist, wird jene Kraft als ein Theil dieser Gesammtkraft
betrachtet, welche nöthig ist, dem Kolben nebst allen damit in Verbindung stehenden
Theilen die Bewegung mitzutheilen. Diese Kraft ist gleich dem Gewichte des Kolbens
und der damit verbundenen Theile auf jene Höhe während der Dauer eines Kolbenhubes
gehoben, welche, als Fallraum betrachtet, dem Kolben eine Geschwindigkeit ertheilt
hätte, gleich der mittlern, womit er den Hub vollbringt. Dieser Ansicht ist z.B. Gerstner der Vater.
Es ist nun allerdings wahr, daß der Kolben diese Kraft benöthigt, um in Bewegung
gesezt zu werden; allein das Bewegungsmoment, welches der Kolben hiebei erhält, geht
für den Nuzeffect keineswegs verloren. Denken wir uns nämlich den Kolben den Weg von
einem Cylinderende zum andern zurüklegend, so fängt seine Geschwindigkeit mit Null
an, wächst allmählich, erhält in der Mitte des Hubes ihr Maximum, nimmt allmählich
wieder ab, und wird am andern Cylinderende wieder gleich Null. Während der ersten
Hälfte des Hubes muß daher allerdings die bewegende Kraft von einem Zeittheilchen
zum andern dem Kolben ein gewisses Bewegungsmoment mittheilen. Ist nun der Kolben in
der Mitte seines Hubes angelangt, so wird er, sich selbst überlassen, sich mit der
erlangten Geschwindigkeit fortzubewegen suchen. Da er dieß indeß nicht kann, so
nimmt seine Geschwindigkeit von einem Zeittheile zum nächsten wieder ab; aus dieser
Ursache muß auch der Kolben von einem Zeittheile zum andern einen Theil seines
Bewegungsmomentes verlieren, welches aber offenbar dem Nuzeffecte der Maschine
wieder zu Gute kommen muß; so daß durch die abwechselnde Bewegung des Kolbens
durchaus keine Beeinträchtigung des Nuzeffectes entsteht.
Ich hoffe, daß diese Zeilen etwas dazu beitragen werden, über die Wirkungsweise der
Kurbel richtigere Ansichten zu verbreiten, als es, nach Hrn. Neukrantz's Abhandlung zu urtheilen, bisher der Fall gewesen zu seyn scheint;
ich wünsche auch, daß gewichtigere Stimmen mit der meinigen sich verbinden mögen,
den hier ausgesprochenen, eine so wichtige mechanische Vorrichtung betreffenden
Ansichten Eingang zu verschaffen.
O. W. v. E.
Tafeln