| Titel: | Ueber eine Verbesserung an Regulatoren, die zur genauesten Zeitmessung bestimmt sind; von Dr. Mohr. |
| Autor: | Dr. Karl Friedrich Mohr [GND] |
| Fundstelle: | Band 81, Jahrgang 1841, Nr. XI., S. 39 |
| Download: | XML |
XI.
Ueber eine Verbesserung an
Regulatoren, die zur genauesten Zeitmessung bestimmt sind; von Dr.
Mohr.
Mit Abbildungen auf Tab. I.
Mohr, über Regulatoren zur genauesten
Zeitmessung.
Der Isochronismus der Schwingungen eines Pendels hängt von vier
Bedingungen ab: 1) daß das Pendel immer gleiche Länge behalte,
2) daß die Schwingungen des Pendels immer denselben
Elevationswinkel behalten, 3) daß die Schwingungen immer in
demselben Medium stattfinden, und 4) daß die anziehende Kraft
der Erde immer dieselbe bleibe. Von diesen vier Bedingungen wird
die lezte, nämlich das Gleichbleiben der Intensität der Schwere,
unbedingt zugegeben, auch würde, wenn sie nicht von selbst
vorhanden wäre, der Mensch durch keine Mittel dieselbe erhalten
oder corrigiren können.
Die erste Bedingung, nämlich die immer gleiche Länge des Pendels,
wird durch die Ausdehnungen der Wärme influencirt, und man hat
bekanntlich die Compensationen erfunden, um diesen Fehler durch
einen neuen, ihm gleichen, aber entgegengesezten zu corrigiren.
Obschon dieser Zweig noch immer neuer
Verbesserungen fähig ist, so ist es dennoch nicht die Absicht,
darauf hier einzugehen, sondern die Wärmecompensation als
gegeben anzunehmen, da die Verbesserungen, welche hier in der
Construction genauer Uhren beschrieben werden sollen, keine der
bekannten Compensationsmethoden ausschließen. Wir haben es hier
nur mit der zweiten und dritten der obigen Bedingungen zu thun,
welche darin bestehen, daß die Pendel immer gleiche Ausschläge
machen sollen, und daß dieselben immer in demselben Medium
stattfinden sollen.
Der lezte Punkt, der Einfluß der ungleichen Dichtigkeit der Luft,
ist an sich der unbedeutendste, und seine Correction ist nicht
direct bezwekt worden, sondern zugleich mit der Correction der
ungleichen Ausschlagswinkel erlangt worden. Es kommt im Effecte
auf das Gleiche hinaus, ob die Schwingungen immer in demselben
Medium geschehen, oder ob durch irgend andere Verhältnisse die
eintretenden Schwankungen in der Dichtigkeit der Luft
unschädlich gemacht werden. In der That ist das leztere der
Fall, denn es werden die Schwingungen des Pendels
außerordentlich klein genommen, dagegen das Gewicht des Pendels
bis zu einer ungewöhnlichen Höhe vermehrt.
Die Schwingungszeiten eines im Kreise schwingenden Pendels sind
bekanntlich, bei gleichbleibender Länge des Pendels, auch von
der Größe der Schwingungsbögen abhängig. Wenn durch t die Dauer einer unendlich kleinen
Schwingung bezeichnet wird, durch y
der halbe Schwingungsbögen und t¹ die Dauer einer Schwingung mit dem
Ausschlagwinkel y, so hat man
bekanntlich
Textabbildung Bd. 81, S. 39
aus welcher Formel man den Werth t¹ für jede beliebige
Elongation finden kann.
Je weiter die Schwingungen gehen, desto größer wird die Zeit t¹, weil y eine positive Größe ist, mit deren
Werth auch die Summe der ganzen Formel steigt. Eine Uhr, welche
also durch vermehrtes Zuggewicht zu größeren Schwingungen
veranlaßt wird und übrigens eine ruhende oder freie Hemmung hat,
muß nachgehen; wird das Zuggewicht vermindert, so wird sie
vorlaufen oder zum Stillstehen kommen; treten Umstände ein,
welche die Kraft des Zuggewichtes modificiren, so müssen auch
diese einen störenden Einfluß auf den Gang der Uhr haben; und
demnach haben vermehrte Reibung, Staub, Verharzung und Frieren
des Oehls, welche einen Theil der erhaltenden Kraft in Anspruch
nehmen, ebenfalls einen störenden Einfluß auf den Ganz
der Uhr. Es ist keine Frage, daß in früheren Zeiten manche
Unregelmäßigkeiten der Uhren, welche auf Rechnung einer
fehlerhaften Compensation geschrieben wurden, größtentheils dem
ungleichen Ausschlage des Pendels zuzuschreiben waren. Um den
Einfluß der Größe des Elongationswinkels deutlich zu machen,
theile ich das folgende, von Stampfer
berechnete Täfelchen mit, zu welchem ich der Uebersichtlichkeit
halber die dritte Columne hinzuberechnet habe.
ElevationswinkelinGraden.
TäglicheRetardation.
Differenz, oderZunahme der
Retardationfür jeden einzelnenGrad
mehr.
1°
0', 1'' . 6
0,'
1'' . 6
2°
0, 6 . 6
0, 5
3°
0,14 . 8
0, 8 .
2
4°
0,26 . 3
0,11 .
5
5°
0,41 . 1
0,14 .
8
6°
0,59 . 2
0,18 .
1
7°
1,20 . 7
0,21 .
5
8°
1,45 . 4
0,24 .
7
9°
2,13 . 4
0,28 .
0
10°
2,44 . 8
0,31 .
4
11°
3,19 . 5
0,34 .
7
12°
3,57 . 5
0,38 .
0
13°
4,38 . 8
0,41 .
3
14°
5,23 . 5
0,44 .
7
15°
6,11 . 6
0,48 .
1
16°
7,3 .
0
0,51 .
4
17°
7,57 . 7
0,54 .
7
18°
8,55 . 9
0,58 .
2
19°
9,57 . 5
1,1 .
6
20°
11,2 . 5
1,5 .
0
Man sieht hieraus den großen Einfluß des Elongationswinkels auf
den täglichen Gang der Uhr. Schwankt dieser Winkel zwischen 1
und 2 Grad, so ist der Gang der Uhr täglich um 5 Secunden
unrichtig, schwankt er zwischen 8 bis 10 Grad, so ist die
Unsicherheit eine ganze Minute; zwischen 18 und 19
beträgt diese Differenz auf einen einzigen Grad eine Minute.
Aus der dritten Columne, worin die Differenzen zweier
benachbarter Stellen angegeben sind, sieht man deutlich, wie die
Retardationen rasch mit der Größe des Winkels steigen, und
ebenso werden diese Differenzen um so kleiner, je kleiner der
Ausschlagswinkel selbst ist.
Es gibt nun zwei Mittel diesen Fehler zu corrigiren: erstlich
durch einen Apparat die Schwingungen selbst gleichzeitig zu
machen. Dieß ist die vom Erfinder der Pendeluhren Hüygens bereits in Vorschlag
gebrachte Anwendung cykloidischer Baken, auf denen sich die
Aufhängefeder des Pendels abwikelt. Diese Methode ist in
lezterer Zeit von Stampfer in Wien
mit Erfolg wieder aufgenommen worden, und von diesem
ausgezeichneten Forscher ist gezeigt worden, daß die Anwendung
cykloidischer Baken dem Uebel wirklich Abhülfe verschaffe,
allein durch die offene Darlegung der zu überwindenden
Schwierigkeiten bei der Darstellung der richtigen cykloidischen
Baken erscheint diese Methode als eine im Allgemeinen rein
unausführbare, und nur jenem zugänglich, welchem die
wissenschaftlichen Hülfsmittel eines Stampfer, unterstüzt durch die mechanischen Talente
eines Starck zu Gebote stehen. Die
Lemberger Uhr steht deßhalb mehr zur Bewunderung da, als zur
Nachahmung. Zwar hat Stampfer auch
gezeigt, daß man statt der cykloidischen Baken solche von
Cylinderform anwenden könne; allein auch hier treten die
Schwierigkeiten wieder aus dem Umstande hervor, daß jedes Pendel
ein Individuum ist, und daß nicht zwei Pendel von gleicher Länge
auch gleiche cylindrische Baken erhalten können.
Es hängt nämlich der Durchmesser der anzuwendenden Cylinderbaken
ab von der Natur der Feder, von der Größe des Ausschlagswinkels,
von der Schwere der Linse und von der Größe des Zuggewichtes.
Allen diesen Bedingungen zu genügen, möchte den meisten
Uhrmachern zu schwierig seyn, und Stampfer's Abhandlung zeigt selbst, daß man durch
unrichtige Form der Baken einen größeren Fehler herbeiführen
kann, als wenn man die Correction ganz wegläßt.
Ich habe deßhalb ein anderes Mittel gesucht, um den Fehler, der
von den ungleichen Ausschlagswinkeln herrührt, auf ein Minimum
zu reduciren.
Ich muß nun zuerst nachweisen, in welcher Art in theoretischer
Beziehung davon Abhülfe zu erwarten ist, und alsdann durch
welche mechanische Mittel ich dieses bezweke.
Wenn die Länge eines Secundenpendels bis an seine äußerste Spize,
wie dieß von einem wirklichen Pendel entnommen ist, 46 preuß. Zoll beträgt, so ergibt sich durch einfache Berechnung,
daß ein Nonagesimalgrad von der äußersten schwingenden Spize
eine Länge hat von
9,689
Linien;
eben so ist
1/2
Grad =
4,844
–
1/4
– =
2,422
–
1/8
– =
1,211
–
1/10
– =
0,9689
–
1/16
– =
0,605
–
1/32
– =
0,3025
–
Es ist nun die Absicht gewesen, die Elevation der
Pendelschwingungen auf eine ungewöhnlich kleine Größe
zurükzuführen. Bei den darüber angestellten Versuchen fand ich,
daß man sehr vortheilhaft einem Secundenpendel eine
Totalbewegung geben kann, welche an seiner äußersten Spize
zwischen 1/2 bis 1 Linie Länge liegt, so daß, wie aus obiger
Tabelle sich ergibt, der Elevationswinkel zwischen 1/16 bis 1/8
Grad liegt. Es hat keine Schwierigkeit, diese Größe sogar noch
zu vermindern, allein wir wollen bei diesen Angaben stehen
bleiben, und den Erfolg für eine Uhr berechnen. Bezeichnet y den halben Schwingungsbogen des
Pendels, so beträgt die tägliche Retardation oder x = 1,645 y² + 0,0000286 y⁴ + etc.
Da unsere Elevationswinkel überhaupt sehr klein sind, so kann man
das von y⁴ abhängige Glied
durchaus vernachlässigen.
Es sey nun y = 1/16°, so
ist
x = 1,645
(1/16)² = 1,645/256 = 0,0064''.
Die tägliche Retardation beträgt also 0,0064 Secunden, oder auf
156 Tage 1 Secunde.
Ebenso beträgt die Retardation für 1/10° täglich 0,01645
Secunden, oder auf 61 Tage 1 Secunde.
Und für y = 1/8° ist die
tägliche Retardation 0,026 Secunden, also auf 38 Tage 1
Secunde.
Nehmen wir nun an, das Pendel könne von 1/16 bis auf 1/8°
in seinen Elevationen schwanken, welche Annahme gewiß exorbitant
ist, da auch bei anderen Pendeln die Schwingung nie auf das
Doppelte gelangt, so beträgt die tägliche Retardation
0,026 – 0,0064 = 0,0196,
also ungefähr 1/50 Secunde, und in 50
Tagen 1 Secunde.
Da aber nun das Pendel niemals so große Schwankungen in seinem
Elevationswinkel erleiden kann, so kann die tägliche Retardation
auch bei weitem nicht 1/50 Secunde erreichen; ja sie wird
überhaupt neben den Fehlern, welche die Compensation noch
zuläßt, gar nicht mehr bemerkbar seyn.
Hiedurch ist nun die Anwendung cykloidischer Baken ganz
vermieden, die Ungleichheit der Schwingungen auf ein Minimum
reducirt, und der Widerstand der Luft wegen der Kleinheit der
Bewegung vollkommen unschädlich gemacht.
Stellen wir noch einige Zahlenresultate zusammen über den Einfluß
eines zunehmenden Elevationswinkels, so haben bis zum Anfange
jenes obigen Täfelchens folgende Zahlen:
Elevationswinkel y.
Tägliche Retardation in
Secunden.
1/16 Grad.
0,0064''
1/0 –
0,0164
1/8 –
0,026
1/4 –
0,102
1/2 –
0,410
5/4 –
0,926
1
–
1,645
Man ersieht also, daß, je kleiner man die Pendelschwingungen
macht, eine desto größere Gleichheit unter sich selbst die
abweichend großen Schwingungen haben müssen. Aus dem Berichte
Stampfer's über den wirklichen
Gang der Lemberger Uhr ergibt sich, daß diese ungeachtet der
cykloidischen Baken dennoch Schwankungen von 2 bis 3 Secunden
täglicher Retardation im Laufe eines Jahres zeigte, eine Größe,
welche die Möglichkeit der Unsicherheit in obiger Construction
um Vieles übertrifft.
Wir haben nun noch darzulegen, in welcher Art wir das Pendel mit
Bestimmtheit des Ganges in kleinen Schwingungen halten
können.
Das Pendel wird zu diesem Zwek oberhalb der Uhr aufgehangen, der
Haken unmittelbar an das untere Ende des Pendels befestigt, und
dieser Haken unmittelbar in das Steigrad eingreifen gelassen,
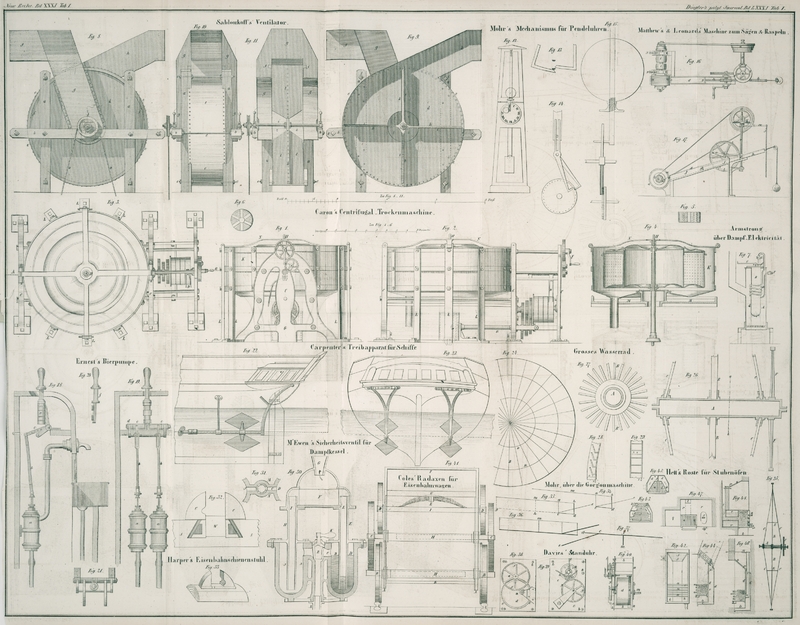
wie dieß in Fig.
12 mit Hinweglassung alles Ueberflüssigen dargestellt
ist. Durch diese höchst einfache, fast ohne Zeichnung
verständliche Einrichtung wird dem Pendel an seiner äußersten
Spize eine eben so große Bewegung mitgetheilt, als ihm sonst an
jener Stelle zu Theil wurde, welche der Länge des Hakens
entsprach.
Da der Haken hier unbeweglich am Pendel befestigt ist, so werden
durch diese Einrichtung erstlich die Reibungen der beiden Zapfen
der Hakenwelle erspart, dann aber auch die durch Elasticität der
Hebelvorrichtung und deren Bewegungen verloren gehenden Kräfte
ebenfalls gewonnen. Das unterste Ende des Pendels ist darum der
vortheilhafteste Punkt, die erhaltende Kraft anzubringen, weil
von hier aus die in Masse zunehmenden Dimensionen des Pendels
eine absolut vollkommene Fortpflanzung 5er erhaltenden Kraft
gestatten. Die äußersten Enden des Hakens haben nicht nothwendig
einen größeren Weg zu beschreiben, als daß eben die
Zähne des Steigrades passiren können.
Von allen verschiedenen Echappements habe ich den einseitigen
Stiftengang als den vortheilhaftesten gefunden.
Der Graham'sche Haken kann durch die
Verlängerung der Pendelstange allein ins Stoken gerathen, wenn
die Pendelstange nicht von Holz ist, wo alsdann durch die
Ausdehnung der Rükwand, woran das Pendel in lezter Instanz
hängt, diese Ausdehnung compensirt wird. Da beim Graham'schen Haken die Zähne in der
Ebene des Rades liegen, so würden die Ballets sehr bald den
Boden der Zahnreihen berühren, und also dem Pendel nur einen
sehr kleinen Schwung erlauben. Jede unvorhergesehene Bewegung
eines 60 bis 80 Pfd. schweren Pendels würde das Steigrad
zertrümmern oder den Haken verlezen.
Der einseitige Stiftengang dagegen bietet folgende Vorzüge
dar:
1) er verträgt bedeutende Senkungen und Hebungen der Ballets,
ohne in Unordnung zu gerathen;
2) beide Ballets wirken im selben Sinne entweder zugweise oder
stoßweise, während beim Graham'schen
Haken ein Ballet immer zieht, das andere aber stößt;
3) da die Stifte nicht in der Ebene des Steigrades liegen, so
kann der Haken eine Schwingung von beinahe dem Durchmesser des
Steigrades machen;
4) eine unrichtige Theilung des Steigrades hat fast gar keinen
Einfluß, sobald nur die beiden Ballets durch die Zahnlüken
passiren können. Der Grund davon liegt darin, daß beim
einseitigen Stiftengang gleich nach einander derselbe Stift an
beiden Ballets passirt, also seine Entfernung gegen andere
Stifte von keinem Belang ist. Beim Graham'schen Haken und dem zweiseitigen Stiftengange,
worunter ich denjenigen verstehe, wo die beiden Ballets um nahe
180° von einander entfernt in den Stiftenkranz
eingreifen, werden meistens 6 bis 10 Zähne eingeschlossen (bei
unserem Pendel würde es genau das halbe Steigrad oder 15 Zähne
seyn), und die Fehler aller dieser Zähne addiren sich
nothwendig, wodurch eine große Fehlersumme entsteht, die ein
Klemmen des Steigrades zur Folge haben kann. Der einseitige
Stiftengang aber macht keine solche genaue Theilung, selbst wenn
man sie haben kann, unumgänglich nothwendig.
5) Die Stellung der Ballets gegen einander läßt sich durch eine
Schraube leicht reguliren, und dadurch die Ruhe auf den Haken
auf ein Minimum reduciren.
Diese Gründe sind überwiegend, um dem Stiftengang den Vorzug vor
jeder anderen Hemmung zu geben. Um den Abfall möglichst klein
zu machen, werden die beiden Ballets so regulirt, daß wenn der
halbcylindrische Stift von dem ersten Ballet abgleitet, er mit
seinem untersten Punkte genau auf die äußerste Spize der Ruhe
des zweiten Ballets auffällt (Fig.
13), und das Zuggewicht der Uhr wird so regulirt, daß
wenn der Stift auf dem äußersten Punkte des zweiten Ballets
angekommen ist, die Pendelschwingung auch zu Ende ist, und der
Stift auf der Ruhe also nicht weiter fortgleitet, sondern im
folgenden Momente sogleich auf der schiefen Ebene abgleiten muß,
der er nun seine Beschleunigung mittheilt. Durch diese sehr
sorgfältige Anordnung wird die Reibung auf der Ruhe möglichst
vermindert, während die Kraft der schiefen Ebene das
Uebergewicht gewinnt. Der Gang nähert sich deßhalb einer
sogenannten freien Hemmung, und ist dieser in Hinsicht des
Effects in allem gleich.
Die Vortheile, welche nun das neue Pendel gegen die ältere
Construction gewährt, sind folgende:
1) der Isochronismus der Schwingungen wird auf ein Maximum
gebracht, indem die Differenzen zwischen den möglichen
Schwingungsbögen unendlich kleiner sind, als sie durch die
Anwendung cykloidischer oder cylindrischer Baken nur jemals
werden können.
2) Der störende Einfluß der ungleichen Dichtigkeit der Luft fällt
weg, weil die Bewegungen des Pendels sehr klein sind, die Massen
des Pendels aber sehr groß genommen werden. Es nähert sich also
die Erscheinung immer mehr der Bewegung im leeren Raume, oder,
wenn man will, der wirklichen Ruhe, wobei kein Widerstand
stattfinden kann.
3) Die Massen der Pendel können ungemein vermehrt werden, wodurch
jede Ungleichheit in der Intensität der erhaltenden Kraft
unschädlich wird.
4) Da bei den Pendelschwingungen der jedesmalige Ersaz an
verlorner Kraft gleich seyn muß der Kraft, womit die Feder hin
und her gebogen wird, und dem Widerstande der Luft, diese beiden
Größen aber hier auf ein Minimum reducirt werden, so geht diese
Uhr auch mit der geringsten Menge der erhaltenden Kraft, d.h.
mit dem leichtesten Gewicht. Hiemit hängt zusammen, daß die
Reibung der Zapfen, der Verschleiß der Räder und namentlich die
Abnüzung der Steigradstifte bedeutend vermindert werden.
Läßt man ein nur 20 Pfd. schweres Pendel in großen Bögen durch
einen Anstoß schwingen, so kommt es sehr schnell auf kleine
Bögen zurük, dann aber schwingt es in kleinen Bögen noch 12 bis
14 Stunden von selbst. Wird aber nun die Masse des Pendels auf
80 Pfd. vermehrt, so bleibt die Schwingungszeit der kleinen
Bögen bedeutend länger, und der Ersaz, welchen das Pendel bei jedem
einzelnen Schlage erhalten muß, wird äußerst gering.
5) Die Uhren werden, weil das Pendel über denselben, und nicht
hinter denselben hängt, weit flacher, und eignen sich deßhalb
besonders gut zum Einmauern; der Raum über einer Reguliruhr ist
ohnehin verloren, es kann also über denselben disponirt werden,
weil man an der Breite gewinnt.
6) Eine eingemauerte Uhr dieser Art kann leicht mit 2
Zifferblättern in 2 Zimmern versehen werden, weil die
Pendelstange dieser Anordnung nicht hinderlich ist, wie dieß bei
allen anderen Uhren der Fall ist.
Die Aehnlichkeit, welche das konische Pendel in der Art der
Aufhängung mit der obigen Construction hat, ist nur scheinbar,
und es kann das konische Pendel in Bezug auf exacte Zeitmessung
mit meinem Pendel nicht verglichen werden. Das lezte Rad beim
konischen Pendel macht alle 2 Secunden einen ganzen Umlauf,
während mein Steigrad nur alle Minuten einen Umlauf hat; die
Reibung beim erstem ist also ceteris
paribus 30mal so groß. Die Beschleunigung des konischen
Pendels nimmt mit der Größe seines Elevationswinkels ungemein
rasch zu, weil die Umlaufszeit gleich ist der doppelten
Schwingungszeit eines Pendels von der Länge der Kegelhöhe, in
dessen Mantel das konische Pendel läuft. Dann ist die Aufhängung
des konischen Pendels äußerst schwierig und der Umstand, daß
sein Schwerpunkt genau in der senkrechten Linie des
Treibestiftes liege, fast gar nicht zu erreichen. Beide Anstöße
fallen bei meiner Construction ganz weg.
Man kann dem Gewichte des Pendels und der Pendelstange beliebige
Formen geben; das Gewicht kann linsenförmig, eine Kugel, ein
Cylinder seyn; der Widerstand der Luft ist nämlich nicht zu
berüksichtigen. Am zierlichsten ist eine runde Pendelstange und
ein Gewicht von Kugelform. Man kann jede Art von
Wärmecompensation gebrauchen.
Oberhalb des Werkes befindet sich ein fester Boden von Holz,
welcher das Werk vor Zertrümmerung schüzt, im Falle das Pendel
sich einmal von seiner Feder losreißen sollte. Durch einen Spalt
geht das untere Ende der Pendelstange. Die Aufhängung des
Pendels mit einer sehr kurzen Feder geschieht an einem Apparate,
welcher kleine Verschiebungen nach Rechts und Links, so wie
aufwärts und abwärts zuläßt, welchen ich jedem sich selbst zu
construiren überlasse, da man diesen Zwek auf verschiedene Art
erreichen kann.
Man kann diese Construction mit Vortheil bei Thurmuhren anbringen
und den Haken so zart construiren, daß sie nie stillstehen
können, sondern durch die bloße Schwere des
Gewichts ohne Anstoß ins Gehen kommen.
Will man den Schlag des Ankers sehr hörbar machen, wie dieß bei
astronomischen Uhren nothwendig ist, so hat man dazu bekannte
Mittel. Man sezt die Stiften weiter aus einander, macht aber die
Breite der Ballets nicht größer; alsdann erhält das Steigrad
eine Beschleunigung von dem Momente, wo der Stift ein Ballet
verlassen hat, bis zu jenem, wo er das andere trifft, und der
Schlag wird stärker. Ein vermehrtes Gewicht wirkt ebenso.
Uebrigens steht die Bedingung eines starken Schlages in einigem
Widerspruch mit der Richtigkeit und Conservation des Werkes.
Eine fernere, sehr bequeme Anbringung des Pendels und des Hakens,
die von der obigen nur darin verschieden ist, daß der Haken
nicht unmittelbar am Pendel befestigt ist, ist durch Fig. 14 und 15
dargestellt.
Das Secundenzifferblatt kann wieder in der Achse der Uhr liegen.
Der Haken greift wie immer in das Steigrad ein, und trägt oben
eine Gabel, in welcher ein horizontaler, von der Pendelstange
ausgehender Stift geführt wird. Läßt man das Pendel in dieser
Gabel auf und ab, so kann man die Größe seiner Bewegung
willkürlich verändern und bei sehr kräftigem Schlage des Ankers
äußerst klein halten.
Tafeln