| Titel: | Ueber einen von Hrn. Combes erfundenen Windmesser, womit man die Luftströmungen in Bergwerksgängen, in Heizungsröhren und Kaminen, und überhaupt in Leitungen von großem Querschnitte messen kann. |
| Fundstelle: | Band 81, Jahrgang 1841, Nr. CVIII., S. 422 |
| Download: | XML |
CVIII.
Ueber einen von Hrn.
Combes erfundenen Windmesser, womit man die
Luftströmungen in Bergwerksgängen, in Heizungsröhren und Kaminen,
und überhaupt in Leitungen von großem Querschnitte messen
kann.
Aus dem Bulletin de la
Société d'Encouragement. Jul. 1841, S.
288.
Mit Abbildungen auf Tab. VII.
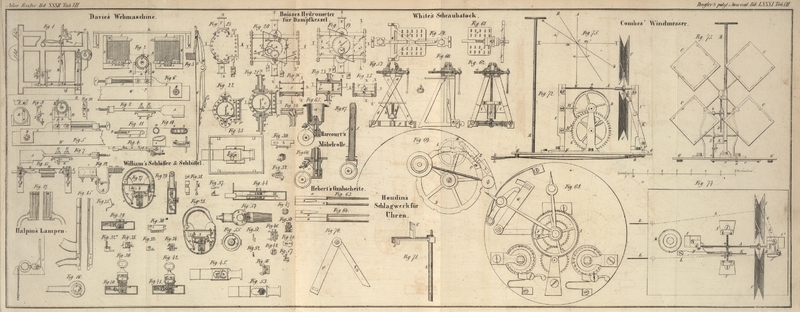
Combes' Windmesser.
Hr. Combes,
Ingénieur en chef des
mines, hat im Jahre 1837 eine Reihe von Versuchen in
Bezug auf die Luftreinigung in den Steinkohlenbergwerken des Dpt. du Nord et de la Belgique
angestellt. Um den Zwek, welchen er sich vorgenommen hatte, zu
erreichen, war es nöthig, die Luftmengen zu messen, welche in
den verschiedenen Minen durch die Wirkung der Saugmaschinen mit
Kolben etc. in Circulation gesezt werden, mit einem Wort, man
mußte die Luftströmungen, welche in gewissen Schachten oder
Gängen stattfanden, bestimmen. Zu diesem Zwek hat er einen
Windmesser ausführen lassen, womit er die Geschwindigkeit der
circulirenden Luft in den Gängen oder in einer Leitung bemessen
konnte, und zwar an verschiedenen Stellen eines und desselben
Querschnitts, senkrecht auf die Achse dieses Ganges.
Dieses Instrument ist von Vorn, von der Seite und von Oben in
Fig.
72, 73
und 74
dargestellt; es besteht aus einer sehr dünnen Achse A, welche in zwei sehr seine Zapfen
endigt, die sich in Lagern von Achat B drehen, und welche vier ebene Flügel C, C, C, C trägt, die alle gleich
gegen eine zur Achse senkrechte Ebene geneigt sind. In der Mitte
der Achse ist eine Schraube ohne Ende a angeschnitten, welche ein Zahnrad D von 100 Zähnen führt, so daß
dieses für jeden Umgang der Achse A
um einen Zahn fortrükt. Die Achse des Rades D trägt einen kleinen Daumen b, welcher auf das Sperrrad E mit 50 Zähnen wirkt; dieses
Sperrrad wird durch eine sehr elastische Stahlfeder F, die an der horizontalen Platte
G, auf welcher das Instrument
steht, angebracht ist, festgehalten. Bei jeder vollen Umdrehung
des Rades D schiebt der Daumen einen
Zahn des Sperrrades vorwärts. Diese beiden Räder sind von 10 zu
10 Zähnen numerirt; das erste von 1 bis 10 und das zweite von 1
bis 5. An der Säule I, die das eine
Lager der Flügelachse trägt, sind zwei Zeiger H, H' befestigt, welche die Zahl der
Zähne, um die jedes Rad fortgerükt ist und folglich die Zahl
der Umdrehungen der Achse A
anzeigen. Mittelst einer Sperrung K
und zweier Schnüre L, L, welche zu
ihrer Bewegung dienen, kann man, von dem Instrument entfernt,
die Kreisbewegung der Flügel hemmen oder ihnen ihre Bewegung,
welche durch den Anstoß der sie treffenden Luftströme entsteht,
gestatten; diese Schnüre sind an den Enden des Hebels c, c, der unter der Fußplatte
befestigt ist, angebracht, und dienen, ihn um den Bolzen d zu drehen. Diesen Hebel bewegt die
Sperrung K mittelst eines
Verbindungsstükes e, welches durch
die Oeffnung f, Fig.
74, der Fußplatte G
geht.
M ist ein kleines verticales, auf
der Platte G aufgeschraubtes
Stängelchen, welches zum Tragen des Windmessers und zum
Festhalten desselben in seinem Kästchen dient. Man kann dieses
Stängelchen bei den Versuchen abschrauben. Um das Instrument
anzuwenden, stellt man zuerst die Nullpunkte beider Räder ihren
Zeigern gegenüber, und bringt alsdann das Instrument auf einen
Fuß in den Querschnitt des Ganges, wo die Luft, die man messen
will, circulirt; die Achse mit den Flügeln wird in die Richtung
der Strömung gestellt, welche die Flügelchen von Vorne gerade so
trifft, wie der Wind die Flügel einer Windmühle. Die Sperrung
hält die Flügel so, daß sie sich nicht drehen können; alsdann
entfernt man sich von dem Instrument und hält dabei in der Hand
die beiden Schnüre der Sperrung; nachdem man sich außerhalb des
Luftstromes gestellt hat, zieht man in einem gegebenen
Zeitpunkte an der einen Schnur der Sperrung und macht dadurch
die Flügel frei, so daß sie sich drehen können. Man zählt nun
die Zeit der Dauer der Beobachtung, welche gewöhnlich mindestens
2 bis 3 Minuten betragen soll; ist die Zeit, welche man sich zur
Dauer der Beobachtung gewählt hat, verflossen, so zieht man an
der andern Schnur der Sperrung und hebt dadurch die Bewegung der
Flügel auf; man liest alsdann auf dem Instrumente die Zahl der
Umdrehungen ab, welche die Flügel während der Zeit ihres
Umlaufens gemacht haben. Jeder Zahn des durch die Schraube ohne
Ende geführten Rades entspricht einem Umgang der Flügelachse,
und die Hunderte von Umgängen werden durch das Rad E von 50 Zähnen angezeigt. Aus der
Zahl der von der Flügelwelle gemachten Umgänge schließt man dann
durch eine dem Instrumente angepaßte Formel auf die
Geschwindigkeit der Luft, welche die Bewegung erzeugt hat.
Das ganze Gewicht der Flügelachse und der Flügel ist 2,67 Gramme.
Die vierekigen Flügel, deren Seiten 0m,0225 lang sind,
wurden aus Rauschgold gefertigt und sind auf einem leichten
Rahmen festgemacht. Die Entfernung des Randes
der Flügel von der Achse, um welche sie sich drehen, beträgt
0m,013.
Mit dem Windmesser wurden 15 Versuche gemacht und der Erfinder
hat daraus eine sehr einfache Formel abgeleitet, worauf er durch
den Druk in Bewegung befindlicher Flüssigkeiten auf eine ebene
bewegliche Fläche geführt wurde. Der Windmesser hat dadurch
einen Grad von Genauigkeit erlangt, der ihn in allen Fällen
schäzbar macht, wo man die Geschwindigkeit der Luft, oder das
Volumen eines Stromes, welcher in einer Leitung von großem
Querschnitt circulirt, bestimmen will.
Es sey a
b, Fig.
75, der Querschnitt einer ebenen Fläche, welche sich
parallel zu ihr selbst nach der Linie X
Y bewegt, die mit der Ebene der
beweglichen Fläche einen Winkel aC
X macht, welchen der Verf. α nennt. Diese Fläche erhalte
den Stoß eines Luftstromes, dessen Geschwindigkeit nach der
Linie A
B, senkrecht zur Linie X
Y, gerichtet ist, und bewege sich
gleichförmig unter dem Druke dieses Stromes in der Richtung C
X. Angenommen nun, daß C
m die Geschwindigkeit des
Vorwärtsschreitens dieser Fläche, der Größe und Richtung nach
vorstelle, und C
n die Geschwindigkeit des Stromes,
so trägt man auf die Verlängerung der Linie C
X, von C
nach Y, die Länge C
m' = C
m, und vollendet das rechtwinkliche
Parallelogramm m
'Cn
r, worauf die Diagonale C
r ihrer Größe und Richtung nach die
relative Geschwindigkeit der Flüssigkeit in Beziehung auf den,
als unbeweglich betrachteten Flügel, darstellen wird.
Nach der allgemein angenommenen Theorie ist der normale Druk der
Flüssigkeit auf eine ebene schief gestoßene Fläche proportional
der Größe der Fläche, dem Quadrate der Geschwindigkeit des
Stromes, projicirt auf die Normale gegen die Fläche und der
Dichtigkeit der Flüssigkeit. Bezeichnet man durch I diesen Druk, durch a die Größe der gestoßenen Fläche
und durch U die relative
Geschwindigkeit, durch π das
Gewicht eines Kubikmeters der Flüssigkeit und durch g die Wirkung der Schwerkraft, so
wird man haben
I = k πa/g
U² sin² MCa (a),
worin k einen
numerischen Coefficienten bezeichnet, welcher sich mit der Größe
der gestoßenen Fläche ändert.
Oder, wenn man durch ν die
durch C
n repräsentirte Geschwindigkeit der
Flüssigkeit bezeichnet, und durch u
die Geschwindigkeit der Fläche ab, welche durch Cm
= Cm' repräsentirt ist, so hat
man
Cr² = U² = ν² + u²,
der Winkel
MCa = MCX –
α.
Ueberdieß gibt das rechtwinkliche Dreiek m'Cr
Textabbildung Bd. 81, S. 425
woraus folgt, daß:
Textabbildung Bd. 81, S. 425
Wenn man die Werthe von U und von sin
MCa in die Gleichung (a) sezt, so wird
I = k πa/g (ν cos α
– u sin
α)².
Weil die durch den mit constanter Geschwindigkeit getriebenen
Flüssigkeitsstrom gestoßene Fläche sich gleichförmig bewegt, so
muß der normale Druk auf die Fläche, projicirt auf die Richtung
der Bewegung, gleich dem Widerstand seyn, welchen diese Fläche,
geschäzt nach derselben Richtung, findet. Nennen wir diesen
Widerstand R und bemerken wir, daß
die Projection des normalen Drukes I
auf die Richtung CX der
Bewegung, gleich I sin α ist,
so hat man
R = I sin α = k πa/g (ν cos α
– u sin α)² sin α,
woraus
Textabbildung Bd. 81, S. 425
In dem zweiten Gliede dieser Gleichung muß man das Zeichen +
nehmen, denn ν muß größer als
u tang α seyn, damit der
Druk des Flüssigkeitsstromes die Fläche von C gegen X fortzutreiben strebt, wie vorausgesezt wurde.
Man kann die Bewegung der Flügel des Windmessers, wenn sie von
der Luft getroffen werden, mit der Bewegung der Fläche, welche
wir so eben betrachtet haben, vergleichen. Wenn man voraussezt,
daß die Widerstände, welche die Flügel, um sich zu bewegen,
erleiden, unabhängig von der Geschwindigkeit sind, so wird die
Formel (b) auf die Bewegung der
Flügel anwendbar seyn, indem man R
als eine Constante, unabhängig von den Geschwindigkeiten ν und u betrachtet. Da der Winkel α ebenfalls constant und die Anzahl der
Umdrehungen der Flügelachse in einer Secunde der Geschwindigkeit
des Mittelpunktes der Flügel proportional ist, so folgt, daß die
Geschwindigkeit ν des
Luftstromes, welcher die Flügel trifft, und die Anzahl der
Umdrehungen der Achse in der Zeiteinheit, durch eine Gleichung
von der sehr einfachen Form: ν = a + b × n verbunden seyn müssen, worin a und b
numerische Coefficienten sind, wovon der zweite nur von der
Neigung der Flügel abhängt, der erste aber nicht nur von dieser
Neigung, sondern auch von der Intensität der Reibung, welche die
Größe von R bestimmt, ferner von der
Dichtigkeit der Flüssigkeit, und endlich von der Größe der
Flügel, welche den Coefficienten k
abändern.
Der Coefficient a hängt von der
Dichtigkeit der Flüssigkeit ab, welche die Flügel des
Windmessers stößt und die im umgekehrten Verhältniß der
Quadratwurzel dieser Dichtigkeit variirt. Um mit großer
Genauigkeit zu operiren, muß man diesen Coefficienten a nach der Dichtigkeit der Luft,
deren Geschwindigkeit man messen will, corrigiren; ist diese
Dichtigkeit beträchtlich, so wird der Coefficient a sehr klein und verschwindet vor
dem zweiten Ausdruk der Formel, so daß die Geschwindigkeit des
Luftstromes alsdann nahezu proportional der Geschwindigkeit der
Flügel seyn muß.
Wenn man einen Luftstrom messen will, welcher in einer etwas
weiten Leitung circulirt, so genügt es, den Windmesser
nacheinander in verschiedene Punkte der Fläche eines und
desselben Querschnittes der Leitung zu sezen, wobei die Achse
der Flügel genau in die Richtung des Stromes gestellt wird. Das
Instrument muß übrigens auf einen geeigneten Fuß gestellt
werden, dessen Volumen sehr klein ist, damit seine Gegenwart in
der Strömung keine merkliche Veränderung erzeugen kann. Man
bestimmt in jedem Punkte die Anzahl der durch die Wirkung der
Strömung hervorgebrachten Umdrehungen der Flügelachse in der
Secunde. Die Flügel des Windmessers werden zuerst durch den
Vorfall stillgestellt, und man läßt sie erst in einem bestimmten
Augenblik laufen, indem man an der zugehörigen Schnur zieht; man
stellt sie nach zwei oder drei Minuten wieder still, indem man
an der zweiten Schnur zieht, und liest hierauf die Anzahl der
während der Dauer der Beobachtung verstrichenen Secunden ab.
Wenn mehrere Versuche in verschiedenen Punkten desselben
Querschnittes auf die Achse der Leitung gemacht wurden, so
braucht man nur das arithmetische Mittel der Zahlen n zu nehmen, die den verschiedenen
Versuchen entsprechen, und hernach durch die gegebene Formel die
Geschwindigkeit ν zu
berechnen, welche diesem arithmetischen Mittel entspricht. Diese
Geschwindigkeit wird die mittlere des Stromes seyn, und gibt,
mit der Fläche des Querschnittes multiplicirt, das Volumen der
in der Leitung circulirenden Luft in Kubikmetern ausgedrükt.
Will man das Volumen eines warmen Luftstromes messen, oder eines
Stromes, dessen Druk merklich von dem gewöhnlichen
atmosphärischen Druke abweicht, so muß man vorher die
Temperatur und den Druk der Luft in dem Strome messen.
Tafeln