| Titel: | Ueber einen von Hrn. Gressien bei Spinnmaschinen angewandten Mechanismus, um eine doppelte Geschwindigkeit mittelst Differenzial-Bewegung hervorzubringen. Von Hrn. B. E. Saladin. |
| Fundstelle: | Band 84, Jahrgang 1842, Nr. IV., S. 7 |
| Download: | XML |
IV.
Ueber einen von Hrn. Gressien bei Spinnmaschinen angewandten
Mechanismus, um eine doppelte Geschwindigkeit mittelst Differenzial-Bewegung
hervorzubringen. Von Hrn. B. E.
Saladin.
Aus dem Bulletin de la Soc. industr. de Mulhausen,
1841, No. 71.
Mit Abbildungen auf Tab.
I.
Saladin, über eine Differenzial-Bewegung für
Spinnmaschinen.
Hr. Gressien bekam eine sehr schwierige Aufgabe zu lösen;
er sollte nämlich Spinnmaschinen die doppelte Geschwindigkeit der ältern Stühle
unter folgenden Bedingungen geben: er durfte die vom Motor herkommende
Geschwindigkeit nicht verändern, mußte die Gestelle der Stühle unverändert lassen,
und durfte nicht mehr Plaz, als für die vorhandene einfache Geschwindigkeit, in
Anspruch nehmen. Durch die ganz besondere Art, wie Hr. Gressien die Differenzialbewegung anwandte, scheint er diese Frage auf
eine sehr sinnreiche Weise gelöst zu haben.
Ich versuche mittelst der Zeichnungen und mit Hülfe folgender Beschreibung den ganzen
Mechanismus verständlich zu machen.
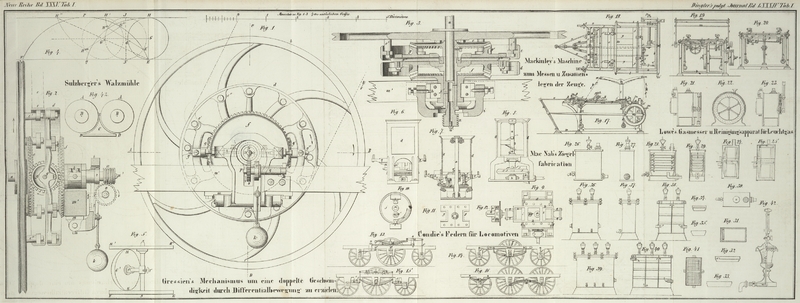
Fig. 1 ist die
Endansicht der Vorrichtung in 1/5 der natürlichen Größe gezeichnet.
Fig. 2 die
Ansicht von der schmalen Seite.
Fig. 3 ein
horizontaler Durchschnitt nach der Linie A
B der Fig. 1.
a Hauptwelle der Spinnmaschine.
b ein großes, auf der Achse a
befestigtes Rad mit Schnurlauf, welches den Spindeln die Bewegung gibt.
c eine festsizende Treibrolle; sie ist mit dem Rade b durch die Schrauben c′, c′ etc. verbunden.
d eine auf einer langen Röhre aufgezogene Treibrolle, die
sich frei auf der Achse a bewegen kann; sie erfüllt
abwechselnd zwei Verrichtungen, nämlich als lose Rolle und als Rolle für die
Erzeugung der doppelten Geschwindigkeit.
e ein auf der Achse a
befestigtes Winkelrad.
f ein Winkelrad mit einer langen Hülse, in Bezug auf die
Anzahl der Zähne dem erstern gleich; am Umfang seiner Hülse ist ein Hals f′ eingedreht.
g, g′ zwei
Winkelgetriebe, die beständig mit dem Rade e in Eingriff
sind; sie drehen sich frei auf ihren Achsen g″,
g′″, welche durch die Rolle d getragen werden, womit sie verbunden sind.
h ein aus zwei Stüken bestehender Ring, welcher die Hülse
des Rades f an der Stelle, wo der Hals f′ eingedreht ist, umgibt; er dient dazu, dieses
Rad fest zu halten und es nachher mit den zwei Getrieben g, g′ in Eingriff zu bringen.
i ein Bügel, welcher zum Ein- und Auslösen des
Rades f dient.
k ein an dem Bügel i
aufgehängtes Gewicht, um das Rad f außer Eingriff zu
bringen.
l ein Schieber mit einem Zapfen, an dem Bügel i befestigt.
m eine Stüze für den Bügel i,
sie ist an dem Gestelle m′ der Spinnmaschine
befestigt.
n eine auf der Achse a
festsizende endlose Schraube.
o das Getriebe des Zählers.
p Achse des Zählers.
q Stüze des Zählers.
r ein auf der Achse des Zählers befestigter Daumen,
welcher zum Abstellen der Maschine, wie bei den meisten Spinnstühlen dient.
s eine auf der Achse p
befestigte Scheibe; an derselben ist ein Einschnitt angebracht, welcher den Zapfen
des Schiebers I aufnimmt, wenn das Rad f ausgelöst werden soll.
t ein auf der Hauptwelle a
befestigter Ring, um zu verhindern, daß die Rolle d sich
zurükschieben und außer Eingriff mit den Getrieben g,
g′ kommen kann.
u ein in der Hauptwelle a
angebrachter Oehlbehälter. Um ihn zu füllen, schraubt man die Schraube n′ ab, und nachdem man mit einem Oehlkännchen
Oehl eingelassen hat, schraubt man sie wieder fest. Dieser Oehlbehälter dient zum
Schmieren des Rohres der Rolle d, so wie der Hülse des
Rades f; die Einrichtung hat das eigene, daß das Oehl,
wenn die Welle sich dreht, vermöge der Centrifugalkraft durch die Oeffnungen zu
entweichen strebt, die in dem Behälter seitwärts eingebohrt sind und so die
erwähnten Stüke gehörig schmiert. Diese Methode das Oehl in der Mitte aufzugeben, um
es nach dem Umfang zu führen, scheint uns bei weitem zwekmäßiger zu seyn, als die
umgekehrte, welche man gewöhnlich befolgt; weil hier zum Vortheil des guten
Schmierens die unvermeidliche Wirkung der Centrifugalkraft benuzt ist, welche im
anderen Falle ein Nachtheil wird.
Denken wir uns den Stuhl in dem Augenblik, wo der Faden anfängt, so umgibt der
Treibriemen die feste Rolle c und theilt dem Stuhl die
einfache Geschwindigkeit, nämlich die langsame und gewöhnliche Geschwindigkeit mit,
bis der Zähler den Riemen von der festen Rolle c auf die
lose Rolle d schiebt, um die doppelte oder beschleunigte
Geschwindigkeit zu erzeugen; aber kurz vorher ehe dieses stattfindet, drükt die
Scheibe s auf den Zapfen l,
so wie auf den Bügel i und das Rad f, bis lezteres mit den beiden Getrieben g, g′ in Eingriff
kommt, welche durch das Rad e bis zu diesem Augenblike
eine unnüze Kreisbewegung erhalten haben, jezt aber der Rolle d die doppelte Geschwindigkeit der Rolle c
mittheilen. Diese Rolle d läuft aber ohne Zwek herum,
bis der Riemen sich um sie gelegt hat und ihr die langsame Geschwindigkeit, welche
er der Rolle c gab, mittheilt; von diesem Augenblike an
wechseln diese beiden Rollen ihre Verrichtungen. Die doppelte Geschwindigkeit,
welche die Rolle d von c
empfing, erhält nun die Rolle c durch die Rolle d und trägt sie folglich auf die Trommeln und Spindeln
über, bis durch den Zähler der Einschnitt der Scheibe s
in Berührung mit dem Zapfen des Schiebers l gebracht
worden ist, so daß durch das Gewicht k das Rad f außer Eingriff gesezt wird und die Rolle d nun lose läuft, weil die Getriebe g, g′ sich frei auf
dem Rade e rollen, ohne eine Wirkung zu erzeugen.
Ich will versuchen, die Theorie dieses Mechanismus so zu erklären, daß mich die
Praktiker verstehen können.
Angenommen, ein Kreis E
G′ H, Fig. 4, rolle auf einer
geraden Linie E
F. Durch sein Fortschreiten wird der Mittelpunkt eine
zweite Gerade G′ G″ parallel mit der ersten E
F beschreiben, und die aufeinander folgenden Punkte
seiner Peripherie werden ebenfalls eine Gerade, mit E
F parallele Linie H
H″ beschreiben, welche doppelt so lange als G′ G″ ist; das
heißt, wenn der Mittelpunkt G nach G′ G″ geht, so befindet sich
der Punkt H in H′,
hernach in H″, wenn man sich die Punkte H′″ und H″″ auf die Gerade niedergeschlagen denkt. E wird ebenfalls nach E′ E″ etc. fortgegangen seyn.
Wenn man folglich, um wieder auf die Figuren 1, 2 und 3 zurükzukommen, annimmt,
daß der Kreis E
G′ H eines der
Winkelgetriebe g, g′
vorstelle, deren Achsen durch die Rolle d getragen
werden; daß ferner die Linie E
F die abgewikelte Peripherie des Rades f und die Linie H
H″ die des Rades e
vorstelle, so begreift man, daß die Rolle d durch die
Bewegung, welche sie den Getrieben g, g′ mittheilt, auf das Rad e dieselbe Wirkung hervorbringen wird, wie der Kreis E
G′ H auf die Linie
H
H″.
Zusaz.
Im Jahre 1813 hat Hr. Perrelet der Société d'encouragement eine AbhandlungSie ist uͤbersezt (mit einer Nachschrift von Hrn. Karmarsch) in den Jahrbuͤchern des k. k.
polytechnischen Institutes in Wien, Bd. VII. S.
242 übergeben, worin er das Princip, auf welchem obige Bewegung
beruht, erklärte; dasselbe wurde damals von einem französischen Künstler Namens Pecquer angewendet, um zweien Wellen, die einander
Bewegung mittheilen, jedes beliebige Geschwindigkeits-Verhältniß zu geben,
welches durch ein gewöhnliches Räderwerk nicht mehr erzielt werden kann; dieß ist z.
B. der Fall, wenn das Verhältniß der Räderachsen durch sehr große, nicht in Factoren
zerlegbare Primzahlen ausgedrükt wird. Da dieses Princip in neuerer Zeit mancherlei
Anwendung gefunden hat, und namentlich auch der Mechanismus, wodurch bei den neuern
Spindelbänken die Geschwindigkeit der Spulen verändert wird, darauf beruht, so
wollen wir einen Auszug aus obiger Abhandlung folgen lassen.
Wenn der Kreis E
G′ H, Fig. 4, sich auf der
geraden Linie E
F wälzt, so beschreibt irgend ein in demselben
angenommener Punkt, z. B. E, einen Weg E
E′, der eine Cycloide heißt, und zu dessen
wesentlichen Eigenschaften es gehört, daß der Abstand E
N zwischen dem Anfangspunkte der Bewegung und einem
beliebigen andern Punkte, in welchem der Kreis die Gerade berührt, dem zugehörigen
Bogen E′ N gleich
ist: E
N = arc. E′ N.
Nehmen wir an, daß der Kreis E
G′ H zwischen zwei
parallelen Linealen E
F und H
H″ sich befinde, von welchen E
F fest, H
H″ aber in der Richtung seiner Länge von E gegen F verschiebbar ist.
Bei dieser Bewegung wird der Kreis E
G′ H durch seine
Reibung an beiden Linealen genöthigt, auf E
F sich zu wälzen, und der Punkt E beschreibt
die Cycloide E
E′ E″ P
F. Aber während dieser Bewegung beschreibt der Punkt H einen Theil einer andern Cycloide H
H′″ Q, welcher
der zweiten Hälfte P
F der ersten gleich ist.
Wenn nun der Punkt E an dem Kreise bis nach E′ in die Höhe gekommen ist, so hat der
Durchmesser E
H die Stellung E′ G′ H′″
angenommen, so zwar, daß der Punkt H′″ in
der zweiten Cycloide liegt, welche der Lage E′
G′ H′″ des erzeugenden Kreises entspricht. Man sieht, daß wenn das
Lineal H
H″ von H nach H″ sich schiebt, der Punkt H dieses Lineals in H′ ankömmt, sobald
der Punkt H des Umkreises nach H′″ gelangt, vorausgesezt, daß die verschiedenen Punkte von
J
H′ nacheinander mit dem Kreise von H′ bis nach J in
Berührung gekommen sind, und daß folglich der Theil J
H′ der Geraden die Ausbreitung des Bogens J
H′″ vorstellt: J
H′ = arc. J
H′″, und da der Bogen E′ N gleich dem Bogen
J
H′″ ist (wegen der Gleichheit der Winkel
E′ G′ N und J
G′ H′″), so müssen auch die zwei ersten Glieder unserer Gleichung
sich gleich seyn, nämlich J
H′ = E
N = H
J. Mithin liegt J in der
Mitte zwischen H
H′, woraus hervorgeht, daß der Mittelpunkt G des Kreises, indem er nach G′ gekommen ist, während H den Ort H″ erreichte, mit einer nur halb so großen
Geschwindigkeit sich bewegt hat, als jene des Lineals H J P
H″ war.
Wenn man beide Lineale ringförmig zusammenbiegt, so erhält man das System Fig. 5; und es
leuchtet ein, daß wenn die obere Scheibe H′ H″ auf der Achse x
y sich dreht, während E
F unbeweglich bleibt, nothwendig die verticale Scheibe
E
G′ H mittelst der
Reibung im Kreise um die nämliche Achse x
y herumgeführt werden muß; und daß hiebei die
Geschwindigkeit, mit welcher der Arm C
V seinen Ort verändert, halb so groß seyn wird als jene,
womit H′ H″
sich dreht; H′ H″ wird einen ganzen Kreis beschrieben haben, wenn C
V erst den halben Umfang durchlaufen hat.
Dieses wird aber nur dann vollkommen richtig seyn, wenn durch die Reibung die
Bewegung genau fortgepflanzt wird. Um diesen Zwek zu erreichen, denke man sich vier
konische Räder so zusammengestellt wie in Fig. 3; die Theilkreise
der Räder e, f vertreten die
Stelle der geraden Linien E
F und H
H″ und die Theilkreise der Getriebe g, g′ die Stelle des
wälzenden Kreises E
G′ H; es wäre daher
nur ein Getriebe g oder g′ erforderlich, denn das zweite hat lediglich den Zwek, die Symmetrie
herzustellen und dem ersten als Gegengewicht zu dienen.
Betrachten wir den Mechanismus in Fig. 3 für sich bestehend,
und das Rad e festsizend auf irgend einer Achse a, während die Achsen der Getriebe g und g′, wie es hier
der Fall ist, mit einer Riemenscheibe d oder auf
dieselbe Art mit einem Zahnrade so verbunden sind, daß sie sich frei um ihre eigene Achse, zugleich
aber mit der Rolle d um die Achse a drehen können; nehmen wir ferner an, daß das Rad f beständig mit g, g′ in Eingriff erhalten werde, daß dieses Rad aber nicht feststehe,
wie in der Figur, sondern sich frei um die Achse a
drehen könne, oder auf einer besondern Achse festsize, die mit a in einer Linie liegt, und ihre besondere Bewegung
erhalten kann, so erhalten wir den Mechanismus, wie er gegenwärtig bei den
Spindelbänken angebracht ist.
Nehmen wir nun an, daß die Räder sich mit gleicher Geschwindigkeit und nach einer
Richtung um ihre Achse drehen, so ziehen sie die Getriebe g, g′ mit gleicher Geschwindigkeit nach
sich. Die Getriebe können sich nicht mehr um ihre Achse drehen, sondern sie werden
mit der Rolle d, womit sie verbunden sind und mit den
Rädern e und f so im Kreise
herumgeführt, als ob alles zu einem Ganzen miteinander verbunden wäre.
Nehmen wir nun an, daß sich zwar beide Näder in derselben Richtung, aber mit
verschiedener Geschwindigkeit drehen, daß z. B. das Rad e sich schneller als das Rad f drehe. Es sey
dabei die Geschwindigkeit des Rades e = V und die von f = V1. Da V größer als V′
angenommen wurde, so kann man die Geschwindigkeit V in
zwei Theile zerlegen in V′ und in V - V′, als dem
Ueberschusse über V′. Vermöge des ersten Theiles
erhält der Arm C
V, Fig. 5, oder die Rolle d in Fig. 3 die
gemeinschaftliche Geschwindigkeit V′, d. h. jene
des Rades f; vermöge des zweiten Theiles, für welchen
das Rad f als ruhend angesehen werden muß, erhält die
Rolle d eine Geschwindigkeit, welche der Hälfte dieses
Ueberschusses (V - V′) gleich ist. Durch Vereinigung dieser beiden Geschwindigkeiten
erhält man für die Geschwindigkeit C, womit die Getriebe
g, g′ und die
Rolle d im Kreise herumgeführt werden:
C = V′ + ½ (V - V′) = V′ - ½ V′ + ½ V= ½ (V + V′); das heißt
die Getriebe werden mit der mittlern Geschwindigkeit beider Räder im Kreise
herumgeführt.
Läßt man beide Räder e und f
sich nach verschiedener Richtung und mit derselben Geschwindigkeit drehen, so werden
sich zwar die Getriebe um ihre eigene Achse drehen, aber die Rolle d, womit die Getriebe verbunden sind, wird an ihrem
Plaze stehen bleiben. Nimmt man aber wieder an, daß die Geschwindigkeit von e in der einen Richtung = V
und die von f in der andern Richtung = V′, und daß V wieder
gleich V′ + V - V′ sey, so werden die Getriebe g, g′ vermöge der
gemeinschaftlichen Geschwindigkeit V′ in
entgegengesezter Richtung ihren Ort nicht verändern, vermöge des Ueberschusses V - V′ werden sie
aber in der Richtung der größern Geschwindigkeit mitgenommen werden, und ihre
Geschwindigkeit in dieser Richtung wird = ½ (V -
V′), d. h. gleich der halben Differenz beider
Geschwindigkeiten seyn.
Nach dem hier Gesagten wird es nicht mehr schwer halten, die Bewegungsweise jedes auf
diese Art zusammengesezten Räderwerkes einzusehen und berechnen zu können.
Tafeln