| Titel: | Anleitung zur Construction des hundertgradigen Aräometers; von Hrn. Francoeur, Mitglied des Instituts von Frankreich. |
| Fundstelle: | Band 85, Jahrgang 1842, Nr. LXXXIV., S. 350 |
| Download: | XML |
LXXXIV.
Anleitung zur Construction des hundertgradigen
Araͤometers; von Hrn. Francoeur, Mitglied des Instituts von Frankreich.
Aus dem Bulletin de la Société
d'Encouragement. Mai 1842, S. 181.
Mit Abbildungen auf Tab.
VI.
Francoeur's Anleitung zur Construction des hundertgradigen
Araͤometers.
1) Dieses Aräometer besteht, wie jene von Baumé,
Cartier u.s.f., aus einer dünnen, cylindrischen und graduirten Röhre M N, Fig. 7, einem
aufgeblasenen Theil oder der Kugel M, und dem Behältniß
eines beschwerenden Körpers L, welcher es beim Schwimmen
in einer Flüssigkeit senkrecht erhält. Nur die Scale mit ihren Abtheilungen ist
verschieden und wird nach folgendem Princip verfertigt.
Man wandelt in Gedanken die Kugel und das
Beschwerungsreservoir in einen Cylinder M A von dem
Volumen und vom Kaliber wie die Röhre M N um, von
welcher er eine Verlängerung ist und supponirt, daß der ganze Cylinder N A. dasselbe Gewicht hat wie das Instrument, welches
aus einem in A beschwerten Cylinder N A von gleichem Gewicht und Volumen wie das Aräometer
erzeugt wird.
Taucht man das Aräometer oder den äquivalenten Cylinder in destillirtes Wasser bei
einer Temperatur von 4°,1 C. oder 3°,28 R., dem Maximum der
Dichtigkeit, so wird das Niveau der Flüssigkeit bei O,
die Null der Scale, seyn. Die eingetauchte Länge O A des
Cylinders nennen wir den Model (module); sie wird in 100 gleiche Theile oder Grade abgetheilt und diese
Abtheilungen werden, von Null ausgehend, sowohl aufwärts als abwärts auf die Röhre
aufgetragen. Die oberen oder positiven Grade dienen für Flüssigkeiten, welche minder
dicht sind als das Wasser; die unteren, für die dichteren Flüssigkeiten, sind
negativ gerade so wie bei den Thermometern.
2) Allein dieses Aräometer von cylindrischer Form wäre sehr unbequem zum Gebrauch; es
wäre zerbrechlich, seine Null nahen Grade wären größtentheils unnüz; die Anwendung
desselben in Flüssigkeiten von geringer Dichtigkeit würde ein sehr tiefes Probeglas
nöthig machen, und in anderen Flüssigkeiten würde es sehr schwierig vertical stehen
bleiben wegen der Länge des über das Niveau hinausragenden Theiles. Auch wollen wir
dem Aräometer seine gewöhnliche Gestalt belassen und der nach der Theorie es
ersezende Cylinder dient uns nur zum besseren Verständniß der Eintheilungsweise der Scale. Es ist uns
nun bloß noch die Länge des Models unbekannt, so wie die der Grade.
3) Man untersucht, wie viel Gramme das Aräometer sammt
seiner Beschwerung wiegt; wir nennen dieß sein Normalgewicht. Senkt man es in reines Wasser, so wird das Niveau am Stiel
den Nullpunkt der Scale anzeigen; man belastet nun den Körper mit einem kleinen, in
Grammen bekannten Gewichte, wodurch er sich in die
Flüssigkeit in einer nach Centimetern bekannten Länge
einsenkt; man multiplicirt das beigefügte Gewicht mit 100
und dividirt das Product mit dem Normalgewicht; so wird
der Quotient die in der Länge der Einsenkung enthaltene Anzahl Grade seyn;
die Scale ist auf diese Weise leicht zu verfertigen, wenn man auch weder den Model
noch das Kaliber der Röhre kennt.
Wenn z.B. das Aräometer 25 Gramme wiegt und sich unter einer Beschwerung mit 1,25
Grammen um 2 Centimeter einsenkt, so findet man, da 100mal 1,25 gleich 125 ist,
welches, mit 25 dividirt, 5 als Quotienten gibt, daß in jeder Länge von 2
Centimetern der Röhre 5 Grade enthalten sind.
Um das behufs dieser Berechnung nöthige Gewicht zusezen zu können, läßt man die Röhre
(den Stiel) oben offen und bringt eine kleine, in Grammen bekannte Quantität
Queksilber hinein, welche man aber später, wenn die Scale fertig ist, wieder
herausnimmt, um den Körper wieder auf sein Normalgewicht zurükzubringen. Es ist gut,
wenn das beigegebene Gewicht so groß ist, daß das zweite Niveau dem oberen Ende nahe
kommt, dann wird damit nämlich eine größere Länge dividirt und die Grade werden um
so genauer.
Statt ein Gewicht beizufügen, kann man auch ein solches abziehen, wo es dann aber
wieder ersezt werden muß; dieselbe Regel hat auch für dieses abgezogene Gewicht ihre
Anwendung. Zum Hinwegnehmen und Zusezen eines Gewichts benuzt man die Erhizung,
gerade wie zum Entleeren und Anfüllen einer Thermometerkugel. Im Allgemeinen sind die Einsenkungen der Röhre unter verschiedenen
successiven Gewichten diesen Gewichten proportional.
4) Um diese Proben leicht anzustellen, läßt man das Ende der Röhre offen und
befestigt innerlich einen kleinen, in Millimeter abgetheilten Streifen Papier; es
ist dieß eine provisorische Scale. Man liest von demselben bei den zwei Proben
sowohl den Punkt ab, wohin Null kommt, also das Wasserniveau unter dem Normalgewicht
des Instruments nach seiner Verfertigung, als auch den Niveaupunkt unter der neuen
Belastung und theilt aus einem anderen Streifen vom selben Gewicht wie
die provisorische Scale, den Zwischenraum nach obiger Regel in Grade ab;
indem man dann diesen an die Stelle der provisorischen Scale bringt, läßt man seinen
Nullpunkt genau mit dem Niveaupunkt unter dem Normalgewicht zusammenfallen; man
befestigt ihn an das Glas mit etwas Siegellak; überzeugt sich endlich, ob dieses
Null richtig steht und das Normalgewicht beibehalten ist und schließt die Röhre an
der Lampe.
5) Gewöhnlich ist es der Fall, daß der Zwischenraum der beiden Niveaux, so wie auch
der Quotient, welcher die Anzahl der inbegriffenen Grade ausdrükt, Bruchtheile
enthält; die Scale ist dann schwer zu machen, weil eine Länge in eine Bruchzahl
gleicher Theile abgetheilt werden müßte; allein man kann diese beiden Zahlen durch
andere ganze ersezen, deren Verhältniß sehr nahe dasselbe ist; was man durch eine
sehr leichte Rechnung findet. (Siehe meinen Cours de
mathématiques pures, No. 595 und 29, 4. Auflage.)
Hat man z.B. gefunden, daß in einer Länge von 28,8 Centimetern 36,6 Grade sind, so
behandelt man das Verhältniß 288/366 wie folgt, nach der Methode des größten
gemeinschaftlichen Divisors:
Textabbildung Bd. 85, S. 351
statt aber den Bruch auf den einfachsten Ausdruk zu reduciren,
indem man seine beiden Glieder durch 6 dividirt, was ihn nur wenig vereinfachen
würde, vernachlässigt man den lezten Quotienten, als wenn 54 durch 24 genau dividirt
würde. Man schreibt 1 unter den lezten beibehaltenen Quotienten, der hier 2 ist; man
schreibt das Product 1 mal 2 = 2 unter den vorausgehenden Quotienten 1; man sagt
ferner 1 mal 2 ist 2 und addirt die Ziffer 1, welche zur Rechten ist, hinzu, wodurch
man 3 erhält; dann 3 mal 3 macht 9, plus 2 gibt 11; 11
mal 1 + 3 = 14; 11 nimmt nun die Stelle von 288 und 14 die von 366 ein und man hat
11/14 als 288/366, sehr nahen Bruch. Man hat also in 11 Centimetern 14 Grade, was
viel einfacher ist als 36,6 Grade in 28,8 Centimetern; wirklich sind, wenn in 11
Centimetern 14 Grade enthalten sind, 36,6 Grade in 28,76 Centimetern. Da übrigens
der Versuch, von welchem die Zahlen 36,6 und 28,8 herrühren, selbst etwas mangelhaft
ist, kann man die Resultate desselben ohne Anstand um ein Geringes abändern; man hat
nun eine bekannte Länge in eine ganze Zahl gleicher Theile einzutheilen.
Vernachlässigt man zwei Quotienten, so hat man 5/4 oder 5 Grade in 4 Centimetern, was zwar
weniger genau, aber auch weniger complicirt ist.
6) Man hat ganz und gar nicht nöthig, den Model zu kennen; kann ihn aber durch diese
Berechnung ebenfalls erhalten. Man messe den Umfang der Röhre mit sehr feiner Seide
ab, dann multiplicire man das Normalgewicht in Grammen mit 3
1/7 und dividire durch das Quadrat des halben Umfanges, in Centimetern; so ist
der Quotient der Model oder die Länge von 100 Graden, in Centimetern.
Wenn also die achtfache Länge irgend eines Theiles der Scale
mit dem Quadrat des Umfanges in Centimetern multiplicirt und durch das
Normalgewicht in Grammen dividirt wird, so ist der Quotient die Anzahl der Grade
dieser Länge.
7) Indem man der Beschwerung das passende Gewicht gibt, kann man es so einrichten,
daß Null ziemlich in der Mitte der Röhre steht; das Aräometer dient dann für
geistige Flüssigkeiten mit seinen positiven Graden aufwärts, und für die
Flüssigkeiten, welche dichter als Wasser sind, mit den gegen unten zunehmenden,
negativen Graden; aber ein solches Instrument könnte nur für solche Flüssigkeiten
gebraucht werben, deren Dichtigkeit jener des Wassers nahe kommt, weil die von Null
entfernten Grade auf der Röhre nicht wohl Plaz hätten.
Die Anwendung verschiedener Aräometer ist daher vorzuziehen; nämlich besonderer für
Flüssigkeiten, die dichter als Wasser sind, wobei der Nullpunkt oder das
Wasserniveau am oberen Ende der Röhre ist, und wieder anderer für minder dichte
Flüssigkeiten, deren Null etwas oberhalb der Kugel ist; man gibt diesen Instrumenten
ein diesen Bedingungen entsprechendes Normalgewicht. Bei den ersteren nehmen die
Grade von Oben nach Unten, bei den anderen von Unten nach Oben zu.
Im Uebrigen wird die Scale, wie schon erwähnt, mittelst eines abzuziehenden oder
zuzusezenden Gewichts verfertigt, welches, nachdem die Scale fertig ist, wieder
dazugethan oder hinweggenommen wird, um das Aräometer wieder auf sein Normalgewicht
zurükzubringen, so daß Null immer am Niveau des reinen Wassers ist.
8) Allein die Null nahen Grade sind selten von Nuzen und nehmen auf der Röhre einen
Raum ein, welcher besser benuzt werden könnte. Man pflegt es so zu machen, daß die
Graduirung auf Gränzen, welche den gewöhnlich zu bestimmenden Dichtigkeiten
entsprechen, beschränkt ist; Null fällt alsdann auf die Verlängerung der Röhre
entweder gegen Unten oder gegen Oben, je nachdem man geringe oder große
Dichtigkeiten bestimmen will. Vermindert man das Kaliber der Röhre, so erhält man
längere Grade und erhöht dadurch die Empfindlichkeit des Instruments, welches dann
nur eine kleine Anzahl Grade anzeigt, die weit genug auseinanderstehen, um noch
Zehntheile abschäzen zu können und die Scale enthält die schwachen Grade nicht mehr.
Auf folgende Weise hat man es in diesen Fällen zu machen.
9) Erster Fall. – Weingeistwaage. Angenommen, das Normalgewicht des belasteten Instruments
sey nicht schwer genug, daß die Kugel sich ganz in das reine Wasser einsenkt;
reducirt man nun in Gedanken das Aräometer auf einen Cylinder durch Verlängerung der
Röhre, so fällt Null auf einen unbekannten, tiefer liegenden Punkt.
Man beschwert das Instrument successive mit zwei kleinen Gewichten; zuerst mit einem,
welches die Kugel und ein kurzes Stükchen der Röhre einsenken macht, und bezeichnet
den Punkt der Wasserhöhe; dann mit einem zweiten, welches die Röhre beinahe ganz
einsinken macht und notirt auch dieses zweite Niveau. Der Zwischenraum dieser beiden
Niveaux ist in Centimetern bekannt. Wendet man nun die in Nr. 3 angegebene Regel
behufs der Graduirung der beiden Punkte an, so multiplicirt
man jedes der beiden zugegebenen Gewichte mit 100 und dividirt die Producte
durch das Normalgewicht. Der dem ersten Gewichte entsprechende Quotient ist
der Grad des ersten Niveau's; der aus dem zweiten zugelegten Gewichte hervorgehende
ist die Anzahl der zwischen den beiden Niveaux enthaltenen Grade und die Summa der
Quotienten ist der Grad des obern Niveau's. Die Scale ist leicht zu machen, weil der
Zwischenraum der Niveaux nur noch in so viele gleiche Grade zu theilen ist, als
dazwischen liegen. Da diese Anzahl der Grade in der Regel ein Bruch ist, so ersezt
man (wie oben Nr. 5 bemerkt wurde) die Zahl der dazwischenliegenden Grade und des
Abstandes durch zwei ganze Zahlen, welche sehr nahe in demselben Verhältniß zu
einander stehen.
Es wiegt z.B. ein Aräometer 21,9 Gramme, und er mußte mit 1,1 Gramm beschwert werden,
damit seine Kugel sich ganz unter das Wasser senkte; ein Gewicht von 2,3 Grammen
machte die Röhre bis nahe ihrem obern Ende einsenken; der Abstand der beiden Niveaux
endlich war 3,7 Centimeter. Dividirt man nun 110 und 230 mit 21,9, so erhält man als
Quotienten 5,02 und 10,50; das erste Niveau erhält 5°,02, das zweite
15°,52, die Summe der beiden Zahlen; es liegen 10°1/2 zwischen den
beiden Niveaux in einem Abstand von 3,7 Centimetern. Man ersezt nun das Verhältniß
10°,5 zu 3,7 Centimetern durch 17° zu 6 Cent., was beinahe dasselbe
ist:
Textabbildung Bd. 85, S. 354
Es müssen demnach in jede Länge von 6 Centimetern 17 Grade eingezeichnet werden und,
indem man den so erhaltenen Abcheilungen die Ziffern 5, 6, 7... 10, 11 gibt,
schneidet man den Papierstreifen so zu, daß er genau dasselbe Gewicht erhält wie die
provisorische Scale und bringt diesen Streifen statt lezterer in die Röhre, indem
man den Punkt des ersten Niveau's an die Ziffer 5°, und den zweiten an
15°1/2 anstehen läßt; man befestigt nun den Streifen an das Glas, schließt
die Röhre und das Gewicht des Aräometers muß 21,9 Gramme betragen.
10) Zweiter Fall. – Säure- und Salzwaage. Gehört das
Aräometer zum Untersuchen von Flüssigkeiten, welche dichtet als Wasser sind, so
nehmen die Grade von Oben nach Unten zu und Null, das Wasserniveau, befindet sich
hier an der obern Verlängerung der Röhre; in das Wasser getaucht, fällt das
Instrument bis auf den Boden des Gefäßes; es ist zu schwer, um zu schwimmen.
Um die Röhre zu graduiren, verfährt man gerade so wie oben gesagt, indem man das
Aräometer durch Hinwegnehmen zweier Gewichte nacheinander leichter macht, die aber
später, wenn die Scale fertig ist, wieder dazu gethan werden müssen; da dieses
Hinwegnehmen keinen andern Zwek hat, als die Länge und die Ziffern der Grade zu
bestimmen, so wird die Communication zwischen der Röhre und dem
Beschwerungs-Reservoir frei gelassen, wie in Nr. 3 erklärt wurde. Das erste
hinweggenommene Gewicht bewirkt, daß ein Stük des obern Theils der Röhre aus dem
Wasser hervorsteht; das zweite macht die Röhre tiefer sinken und man erhält so das
zweite Niveau, welches sich etwas oberhalb der Kugel befinden muß. Dividirt man das
Hundertfache jedes zugegebenen Gewichts durch das Normalgewicht, so ist der erste
Quotient der Grad des obern Niveau's, der zweite die Anzahl der zwischen beiden
Niveaux enthaltenen Grade und das untere erhält als Grad die Summe der Quotienten.
Man hat somit alle zum Eintheilen der Scale nöthigen Elemente.
Angenommen, ein 24 1/2 Gramme wiegendes Aräometer sey zu schwer, um über dem Wasser
zu schwimmen, man nehme 3,1 Gram. von seiner Beschwerung, und der obere Theil der
Röhre erhebe sich nun über das Niveau; beim Hinwegnehmen weiterer 1,5 Gramme sey das
Niveau etwas oberhalb der Kugel, 5,32 Centimeter vom ersten Niveau entfernt, so wird
die Scale auf folgende Weise construirt. Man dividirt 310 und 150 durch 24,5, was die Quotienten
12,65 und 6,12 gibt, woraus folgt, daß das obere Niveau 12°,65 erhalten muß
und daß 6°,12 bis zum untern Niveau vorhanden sind, welches 18°,77
erhält; da aber die Zahlen 6°,12 und 5,32 Cent. Bruchzahlen sind, so werden
sie durch 23° und 20 Centim. ersezt, welche beinahe in demselben Verhältniß
zu einander stehen.
Textabbildung Bd. 85, S. 355
Man sieht demnach, daß 20 Centim. in 23 Grade getheilt werden müssen, was eine Scale
von gleichen Theilen zu bilden gestattet, welche von Oben abwärts die Ziffern 12,
13, 14... bis 19 erhalten. Man bringt diese Scale anstatt der in Millimeter
abgetheilten in die Röhre (nachdem sie vorher im Gewicht gleich gemacht wurden)
indem man die beiden Niveau-Punkte, deren einer bei 12°,65 und der
andere bei 18°,77 erhalten wurde, genau anpaßt. Zulezt bringt man die beiden
herausgenommenen Gewichte, nämlich 3,1 Gram. + 1,5 Gram. = 4,6 Gram. wieder zur
Beschwerung, damit das Aräometer sein Normalgewicht, 24,5 Gram., wieder bekommt und
schließt die Röhre.
Es sind also folgende Operationen vorzunehmen, um die Scale eines Aräometers zu
construiren, wenn diese Scale die Null nahen Grade nicht zu enthalten braucht.
1) Bei einer Weingeistwaage muß ihr Normalgewicht leicht
genug seyn, damit die Kugel im Wasser nicht ganz untertaucht; man wägt diesen
Körper.
Dann gießt man in die Röhre etwas Queksilber, bis das Niveau des Wassers über der
Kugel ist, bezeichnet dieses Niveau und wägt; nun gießt man noch einmal Queksilber
zu, bis die Röhre beinahe ganz untertaucht; man notirt auch dieses zweite Niveau und
wägt den Körper. Man hat nun drei Gewichte, deren Differenzen die zwei zugesezten
Gewichte sind: man kennt diese Gewichte in Grammen, so wie den Abstand der beiden
Niveaux in Centimetern.
Nun dividirt man das Hundertfache jedes beigegebenen Gewichts durch das Normalgewicht
und multiplicirt die Quotienten mit diesen respectiven Gewichten; das erste Product
ist der Grad des untern Niveau's, das zweite ist die Anzahl der in dem die beiden
Niveaux trennenden Raume erhaltenen Grade; die Summe der Quotienten ist der obere
Grad. Die Scale ist leicht anzufertigen, weil man weiß, wie viel Grade zwischen den
Niveaux liegen; man braucht nur noch diese Zahl und den Abstand durch andere ganze Zahlen
zu ersezen, welche so ziemlich in demselben Verhältniß zu einander stehen.
Will man den Model finden, so multiplicirt man das Normalgewicht in Grammen mit dem
Abstand der Niveaux in Centimetern und dividirt das Product durch das zweite
zugesezte Gewicht; der Quotient ist dann der Model in Centimetern, wovon der
hundertste Theil die Länge eines Grades ist.
2) Bei einer Säurewaage belastet man zuerst die
Beschwerung nur mit einem Gewichte, welches hinreicht, um das Niveau des Wassers
etwas über die Kugel zu erheben; man notirt dieses Niveau und wägt; dasselbe
wiederholt man, nachdem man so viel Queksilber hinzugesezt hat, daß die Röhre
beinahe ganz untertaucht; man kennt die Differenz dieser Gewichte in Grammen und den
Abstand der beiden Niveaux in Centimetern. Endlich sezt man ein zweites beliebiges
Queksilbergewicht hinzu, um das Normalgewicht zu bilden, welches man so wählt, daß
man mit dem Instrument alle vorkommenden Dichtigkeiten jener Flüssigkeiten messen
kann.
Man dividirt das Hundertfache der beiden zugesezten Gewichte durch das Normalgewicht;
der erste Quotient ist der Grad des untern Niveau's, der zweite die Anzahl der
zwischen den Niveaux liegenden Grade und man bildet die Scale wie vorher; das
Uebrige ist eben so.
Es ist zu bemerken, daß je schwerer das Normalgewicht eines Aräometers ist, desto
länger der Model und die Grade bei einem gegebenen Kaliber der Röhre sind; die Grade
wachsen proportional den Normalgewichten; der Model und die Grade behalten aber ihre
Längen, wenn das Normalgewicht und das Kaliber der Röhre constant sind; es wechselt
also die Form und das Volumen der Kugel, ohne daß die Scale sich ändert, aber unter
Verrükung des Nullpunkts auf der Röhre. Nachdem man einmal die Scale gebildet hat,
kann man dieselbe also beibehalten, wenn man die Kugel verändert, vorausgesezt, daß
das Normalgewicht dasselbe bleibt und Null an der gehörigen Stelle befestigt wird.
Man wird bald finden, daß das Normalgewicht auch so gewählt werden kann, daß ein
gegebener Punkt der Röhre einen vorher bestimmten Grad enthält.
11) Man kann auf folgende Weise die Unannehmlichkeit vermeiden, daß man das
Beschwerungs-Reservoir ausleeren und wieder füllen muß, um die Scale zu
graduiren. Man nimmt eine hinlänglich dichte Flüssigkeit, z.B. eine Säure oder eine
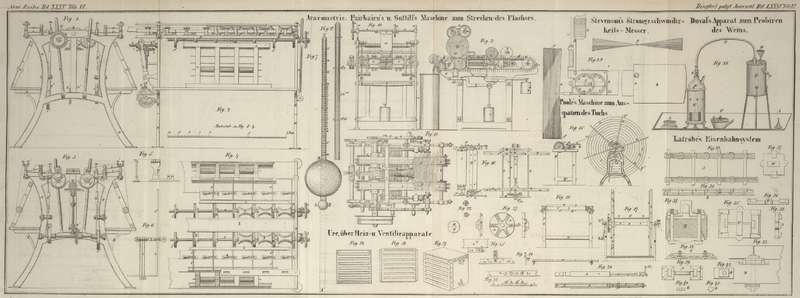
Salzlösung, senkt das zu graduirende Aräometer hinein und bezeichnet den Punkt i, Fig. 8, der
Flüssigkeitshöhe, dessen Grad man findet, indem man entweder das Aräometer mit einem
andern schon abgetheilten vergleicht, oder indem man das specifische Gewicht dieser Flüssigkeit
auf gewöhnliche Art ausmittelt: dividirt man dieses Gewicht
minus eins durch das Hundertstel desselben
Gewichts, so wird der Quotient der Grad des Niveau's i seyn. Man beschwert nun innerlich das Aräometer mit einem
kleinen Gewicht, welches die Röhre in derselben Flüssigkeit bis r einsinken macht; i r ist
in Centimetern bekannt. Die Anzahl der in dem Zwischenraum i
r der beiden Niveaux enthaltenen Grade ist der Quotient des Zusazgewichtes, multiplicirt mit 100, minus dem Grad des Punktes
i, dividirt durch das
Normalgewicht. Die übrige Operation ist nicht schwierig, weil es sich nur
darum handelt, den Raum i r in so viele gleiche Theile
abzutheilen, als Grade darin enthalten sind.
Man benuzt z.B. eine Säure, deren specifisches Gewicht 1,231 ist und taucht das
einzutheilende Aräometer hinein, welches 24,5 Gramme wiegt; das Niveau zeigt sich
bei einem Punkte i; der Grad dieses Punktes ist der
Quotient von 0,231, dividirt durch 0,01231, oder 18°,77. Man beschwert nun
die Röhre mit dem Gewicht von 1,845 Grammen, wodurch das Niveau auf r kommt; die Länge i r
beträgt 5,32 Centimeter. Multiplicirt man das Zusazgewicht 1,845 mit 81,23 =
100° – 18°,77, so ist das Product 149,869, welches, durch das
Normalgewicht 24,5 dividirt, den Quotienten 6,12 gibt; es liegen also 6,12 Grade in
dem Zwischenraum i r von 5,32 Centimetern, beinahe 23
Grade in 20 Centimetern.
12) Zu machen, daß das Normalgewicht eines Aräometers der Art
ist, daß ein gegebenes Gewicht der Röhre einen bekannten Grad bekommt.
Man wägt zuerst das Instrument und beschwert es dann im Wasser mit so viel Gewicht,
daß das Niveau mit dem an der Röhre angegebenen Punkt gleichsteht. Die Summe dieser beiden Gewichte oder das Gesammtgewicht des
so beschwerten Instruments, dividirt durch 1 + dem
Hundertstel der gegebenen Zahl der Graduirung, gibt als Quotienten das
Normalgewicht, welches das Instrument haben muß, um die auferlegte
Bedingung zu erfüllen. Man bringt also in das Beschwerungs-Reservoir die
gehörige Belastung, um dieses Normalgewicht zu erhalten, wohlverstanden mit
Hinweglassung des Zusazgewichts. Die übrige Operation laͤuft wieder auf das
schon Gesagte hinaus.
Handelt es sich um ein Aräometer zum Wägen dichterer Flüssigkeiten als Wasser, so ist
das Gewicht ein abzügliches und der in der Regel angegebene Divisor ist 1 – ein Hundertel des
für das erste Niveau gegebenen Grades.
Beispiel. Eine Weingeistwaage soll an einem Punkte ihrer
Röhre, etwas oberhalb der Kugel, 5 Grade zeigen. Damit dieser Punkt am Niveau des
Wassers steht, wurde gefunden, daß das Instrument beschwert werden müsse, bis sein
Gesammtgewicht 23 Gram. beträgt; dividirt man 23 durch 1,05, so ist der Quotient
21,9 Gr., woraus hervorgeht, daß das Normalgewicht des Aräometers 21,9 Gr. betragen
muß. Man nimmt also 1,1 Gram. von der Belastung weg und läßt das Uebrige in die
Beschwerung des Instruments eingehen, welches dann 21,9 Gramme wiegt und an dem
gegebenen Punkt der Röhre den Grad 5 hat.
Man will, daß eine Säurewaage 12°,65 an einem gegebenen Punkt der Röhre gegen
das obere Ende zu zeige und fand, daß, damit das Wasser an diesem Punkte sein Niveau
habe, das Instrument um so viel leichter gemacht werden müsse, daß es nur mehr 21,4
Gramme wiegt. Dividirt man nun 21,4 durch 1–0,1265 oder 0,8735, d.h. 214000
durch 8735, so ist der Quotient 24,5 Gramme das dem beschwerten Aräometer zu gebende
Gewicht. Man bringt demnach in das Beschwerungs-Behältniß außer dem, was von
der ersten Belastung bleibt, ein Gewicht von 3,1 Grammen, damit das Normalgewicht
zulezt 24,5 ist.
13) Aräometer mit mehreren Scalen. Aendert man das
Gesammtgewicht eines Aräometers, so ändert man auch seinen Model, folglich auch die
Länge seiner Grade und die Lage des Nullpunkts. Wird das Normalgewicht schwerer, so
werden der Model und die Grade länger. Man kann sonach an einer Aräometerröhre
mehrere Scalen anbringen, deren jede einem besondern Normalgewicht entspricht.
Belastet man also eine Röhre innerlich oder an ihrem obern Ende mit einem kleinen
Gewichte, so wird dasselbe Instrument eine neue Scale annehmen und kann zum Messen
anderer Dichtigkeiten dienen.
Wenn z.B. ein 100gradiges Aräometer von 10 bis 25° unter 0 zeigt, so kann man,
indem man ein passendes Gewicht zusezt, auf einer andern Scale die Dichtigkeiten von
25 bis 35 Graden messen; diese Grade werden länger seyn als die erstern: diese
zweite Scale wird nach demselben Verfahren graduirt. Man kann es so machen, daß der
stärkste Grad einer Scale der schwächste der andern wird und eine einzige Röhre
leistet nun dasselbe, wie wenn ihre Länge verdoppelt worden wäre. Eine dritte Scale
kann einem andern Normalgewicht entsprechen u.s.f.
14) Die Aräometer mit mehreren Scalen werden in der Regel von Metall, hohl und sehr
dünn gemacht. Die Scalen werden auf die Seiten einer prismatischen Röhre gravirt und
jede bezieht sich auf ein eigenes Normalgewicht, d.h. auf ein specielles
Zusazgewicht. Sie sind nicht so zerbrechlich wie die gläsernen, können aber für
Säuren nicht gebraucht werden. Man muß sich in Acht nehmen, daß sie keine Beulen
erhalten, wodurch sie fehlerhaft würden, weil das eingetauchte Volumen nicht mehr
dasselbe wäre. Die Zusazgewichte werden entweder oben an der Röhre oder innerlich
angebracht, und wenn man sie unten in der Nähe der Beschwerung anschraubt, um die
verticale Haltung des Instruments zu sichern, so müssen ihre Volume gleich seyn,
damit das eingetauchte Volumen immer dasselbe ist.
Falls man sich, nachdem die Scale eingetheilt ist, um die Communication der
Beschwerung und der Röhre abzuschließen, der Flamme bedient und die Kugel aus ihrer
Form bringt, so kann die Scale noch gebraucht werden, wenn man nur den Nullpunkt
auf- oder abrükt und ihn an das Wasserniveau sezt, oder, was auf dasselbe
hinauslaͤuft, den Angaben des Aräometers, als constante. Correction, die
Anzahl Grade hinzusezt oder hinwegnimmt, welche die beiden Stellungen des
Nullpunktes von einander trennt.
15) Aus dem Gesagten ersieht man die Vorzüge des hundertgradigen Aräometers im
Vergleich mit jenen von Baumé, Cartier und
anderen. Es ist nichts Willkürliches in seiner Construction als die Eintheilung des
Models in hundert gleiche Theile; die Scale ist stets leicht zu verzeichnen und
jeder kann ihre Genauigkeit durch sehr einfache Versuche prüfen, Vorzüge, welche
keines der gebräuchlichen Instrumente dieser Art besizt. Es hat im Uebrigen nur die
von jedem Aräometer unzertrennlichen Mängel.
Man kann hundertgradige Aräometer zum Wägen besonderer Flüssigkeiten construiren,
deren Dichtigkeiten zwischen gewissen gegebenen Gränzen begriffen sind und die Grade
ausgedehnt genug machen, um die gewünschte Empfindlichkeit herauszubringen, indem
man der Röhre ein dünnes, sehr ausgezogenes Kaliber gibt. So kann man Syrupwaagen machen, welche 18 bis 24 Centesimalgrade
angeben, Wein- oder Mostwaagen von 0 bis 7 Graden, Weingeistwaagen
von 4 bis 20 Graden, Milchwaagen von 0 bis 4 Graden, Aetherwaagen von 14 bis 41 Graden u.s.f.
16) Die zum Eintheilen der Scalen oben angegebenen Versuche sind nur zur Construction
der Musteraräometer und zur Prüfung der Instrumente,
welcher man sich bedient, nöthig; denn um für den Handel wohlfeile Aräometer liefern
zu können, machen es die Fabrikanten wie mit den Thermometern und bedienen sich der
Muster- (oder Aich-) Instrumente. Man verschafft sich mehrere
Flüssigkeiten, deren aräometrische Grade mittelst eines Muster-Instrumentes
ermittelt sind, taucht das einzutheilende Instrument in zwei dieser Flüssigkeiten,
worin es schwimmen kann und bezeichnet die Punkte, wo das Niveau ansteht; die
Graduirung dieser Punkte ist schon bekannt und man braucht nur mehr ihren
Zwischenraum in eine gewisse Anzahl gleicher Theile einzutheilen.
Das Gewicht und die Dimensionen der Theile eines Aräometers müssen, da sie die
constituirenden Elemente der Scale ausmachen, für diese Scale constant bleiben; man
muß daher zu verhüten suchen, daß sich Schmuz oder Luftbläschen auf seiner
Oberfläche anhängen.
17) Obwohl wir die Bedingung gesezt haben, daß das zu den Proben dienende Wasser auf
dem Maximum seiner Dichtigkeit (auf einer Temperatur von 4,1° C.) sich
befinde, so kann man doch, da die Dichtigkeit dieser Flüssigkeit mit dem Steigen der
Temperatur sich nicht stark verändert, auch bei der gewöhnlichen Lufttemperatur
operiren, um die Eintheilung der Scale zu erhalten, und einige Grade über 4°
sind auf die Graduirung von gar keinem Einfluß j da aber
die Wärme die Substanz des Aräometers selbst merklich ausdehnt und sein Volumen
vergrößert, so soll man bei Verfertigung einer aräometrischen Scale sich von 4 bis 6
Graden nicht zu sehr entfernen.
18) Die Flüssigkeit übt auf die Röhre beim Benezen derselben ihre Anziehungskraft
aus, besonders wenn die Röhre dünn und stark ausgezogen ist. Das Niveau, womit sie
sich anlegt, liegt etwas über dem des Wassers; lezteres aber ist es, welches
angezeichnet werden muß. Wenn man also die beiden, den Eintheilungen zu Grunde
liegenden Punkte festsezt, darf man den Fehler nicht begehen, die Spize der
Flüssigkeitssäule als das Niveau zu betrachten. Indem man die Röhre schwach mit Oehl
bestreicht, vermeidet man Fehler dieser Art.
19) Ein dem 100gradigen Aräometer eigenthümlicher Vorzug ist, daß es das specifische
Gewicht der Flüssigkeiten so genau angibt, als es bei Versuchen mit diesem
Instrumente nur immer möglich ist; d.h. die Irrthümer rühren niemals von der
Berechnung her, welche im strengsten Sinne genau ist, sondern von der Bestimmung des
Punktes der Röhre, wo das Niveau stehen bleibt, von dem Ablesen des Grades. Nach der
Theorie muß das erhaltene specifische Gewicht genau seyn; es kann nur in Folge
unrichtiger Beobachtung etwas fehlerhaft ausfallen. Die andern Aräometer bieten bei
weitem diese Genauigkeit
nicht; denn außer den so eben erwähnten Beobachtungsfehlern gibt es dabei noch viel
größere, von ihrer Scale-Einteilung herrührende Fehlerquellen. Wirklich sind
unter zwanzig von den geschiktesten Physikern gelieferten Tabellen zur Vergleichung
der Aräometergrade mit den Dichtigkeiten der Flüssigkeiten, nicht zwei auch nur in
einigen Graden übereinstimmend.
Zu solchen Vergleichungen dient folgende Regel:
Bei Weingeistwaagen dividirt man 100 durch 100 + dem Grade des
hunderttheiligen Aräometers, welcher das Niveau der Flüssigkeit angibt; der
Quotient ist das specifische Gewicht, jenes des Wassers als Einheit
angenommen.
Bei Säurenwaagen dividirt man 100 durch 100 – dem
Aräometergrad.
Ein Branntwein zeigt z.B. 6 Centesimal-Grade; der Quotient von 100 dividirt
durch 100 + 6 oder 106 ist 0,943396, das verlangte specifische Gewicht. Glaubt man,
daß die Beobachtung etwas zweifelhaft seyn könnte, so braucht man nur die lezten
Decimalen zu vernachlässigen, welche, wenn sie auch theoretisch höchst genau sind,
doch einen Einfluß erleiden konnten durch die Fehler des Versuchs, so daß man gerade
nicht genau 6 Grade für die Flüssigkeit erhalten hätte. Zeigt z.B. eine Säure 16
Centesimal-Grade, so dividirt man 100 durch 100 – 16 = 84 und der
Quotient 1,190476 ist das specifische Gewicht der Säure, wenn man in Berüksichtigung
der Beobachtungsfehler nicht bloß die ersten Ziffern beibehalten will.
Dieß ist der Grund, warum meine Tabellen die specifischen Gewichte nur mit drei
Decimalen angeben.
Vergleichung der positiven Grade des Hundertgradigen
Aräometers mit jenen von Baumé und Cartier, so wie mit den specifischen
Gewichten.
Textabbildung Bd. 85, S. 362
100gradig. Aräometer; Baumé;
Cartier; Specifisches Gewicht
Tabelle zur Vergleichung der negativen Grabe des
hundertgradigen Aräometers mit jenen von Baumé's Säurewaage und mit den
specifischen Gewichten.
Textabbildung Bd. 85, S. 363
100gradig. Aräometer; Baumé;
Cartier; Specifisches Gewicht
Tafeln