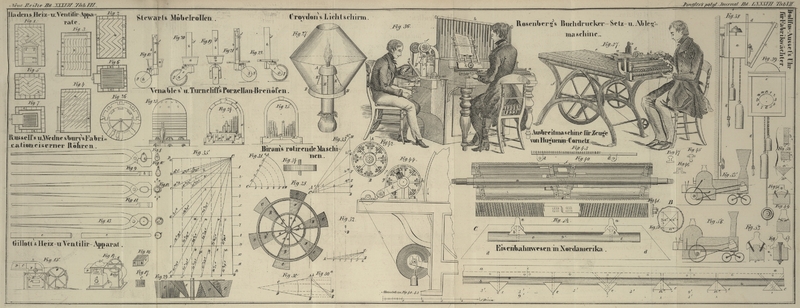
| Titel: | Biram's Verbesserungen in der Construction und Anwendung rotirender Maschinen (Windmühlen, Wasserräder, Ruderräder etc.). |
| Fundstelle: | Band 87, Jahrgang 1843, Nr. LXXXVII., S. 334 |
| Download: | XML |
LXXXVII.
Biram's Verbesserungen in
der Construction und Anwendung rotirender Maschinen (Windmuͤhlen,
Wasserraͤder, Ruderraͤder etc.).
Aus dem Mechanics' Magazine. Okt. 1842, S.
321.
Mit Abbildungen auf Tab.
VII.
Biram's Verbesserungen in der Construction und Anwendung
rotirender Maschinen.
Die Flügel der Windmühlen und anderer ähnlicher durch den Wind bewegten Maschinen
bestehen gewöhnlich aus ebenen Flächen, die unter beliebig gewählten, öfters höchst
ungeeigneten Winkeln schief zu der Ebene der Bewegung angeordnet sind; auch die
Schaufeln der Wasserräder bilden in der Regel ebene, jedoch rechtwinkelig zur
Bewegungsebene eingesezte Flächen. Hr. Biram weist
zunächst nach, daß in diesen beiden Fällen eine gewisse, den Flügeln oder Schaufeln
ertheilte Krümmung, oder mit andern Worten, eine stufenweise Reduction der schiefen
Winkelstellung im Verhältnis zu dem Abstande von der Achse, meistens einen größeren
Effect liefert als jede andere Form.
Es stelle z.B. ABC, Fig. 31, den sechsten
Theil eines durch die Rotation einer Windmühle beschriebenen Kreises vor, so ist die
Sehne des Bogens AB dem Halbmesser AC gleich. Es seyen ferner die Linien AC und CB in
sechs gleiche Theile 1, 2, 3, 4, 5, 6 getheilt, so daß die zu den Bögen der
Eintheilungen 55, 44, 33, 22 und 11 gehörigen Sehnen beziehungsweise den Abständen
C₅, C₄, C₃, C₂ und C₁ gleich sind. Um nun den Winkel zu ermitteln,
welchen ein Windflügel in jedem Abstande von der Achse C
bilden soll (den Winkel am äußersten Ende oder an irgend einem andern Punkte als
gegeben vorausgesezt), construire man den verticalen Durchschnitt Fig. 32, in welchem die
Linie AB dem Halbmesser AC in Fig. 31 gleich ist, und
theile denselben in sechs gleiche Theile 1, 2, 3, 4, 5, 6. Dann ziehe man ein Perpendikel C₆ von unbestimmter Länge und construire den
Winkel CAB, wenn derselbe am äußersten Ende, oder
den Winkel C₃B, wenn er in der Mitte des Segels
gegeben seyn soll. Der Abstand des Durchschnittspunktes C von 6 gibt die Tiefe des Cylinders oder des Raumes an, in welchem die
Windflügel sich drehen sollen, von der Seite nämlich betrachtet und unter der
Annahme, daß das Rad sechs Flügel besizt und so eingerichtet ist, daß es den ganzen
Windcylinder auffängt. Soll die Tiefe des Cylinders ein anderes Verhältniß erhalten,
oder soll die Dimension eines jeden Windflügels eine andere als der sechste Theil
eines Kreises seyn, so gibt eine in verhältnißmäßiger Höhe durch CB zu AB
parallel gezogene Linie die Tiefe des verlangten Cylinders an. Man ziehe nun von dem
Durchschnittspunkte C aus die schiefen Linien C₁, C₂, C₃, C₄ und C₅, so sind die Winkel C₁B, C₂B, C₃B, C₄B und C₅B diejenigen Winkel, welche der Windflügel in den Entfernungen
₁B, ₂B, ₃B, ₄B,
₅B von dem Mittelpunkte oder der Achse B, Fig.
32, mit der Ebene der Bewegung bilden sollte. Denn angenommen, der Winkel
CAB, Fig. 32, sey dem Winkel
des Flügels mit der Ebene der Bewegung an seinem äußersten Ende gleich und der Wind
habe die Richtung D₃, so trifft er das Flügelende
unter dem Winkel ACB, Fig. 32, und treibt es
zurük. Unter der Voraussezung, daß die Maschine unbelastet und ohne Reibung geht,
werden sich die Punkte 55, 44, 33, 22 und 11 um die Winkel C₁B, C₂B, C₃B, C₄B und C₅B bewegen, während der Wind die Streke CB, Fig. 32, zurüklegt.
Hieraus geht hervor, daß jeder Theil des Flügels nicht mehr als den seiner Lage
entsprechenden verhältnißmäßigen Widerstand dem Winde entgegensezen und genau mit
derjenigen Geschwindigkeit zurükweichen wird, welche der Bewegung des Windes die
geringste Störung darbietet.
Den Einfluß des Neigungswinkels auf die Geschwindigkeit des bewegten Körpers
erläutert Hr. Biram noch deutlicher, indem er Wasser
anstatt Luft als Mittel, worin der Körper sich dreht, annimmt.
ABCD, Fig. 33, sey ein
Parallelogramm gleich dem Umfange eines durch die Umdrehung der Flügel beschriebenen
Cylinders, und die schiefen Linien C₁, C₂,
C₃ und C₄ bilden die
verschiedenen Winkel der Flügelenden mit der Ebene der Bewegung, z.B. 14°, 26
2/3°, 45° und 56 1/3°. Gesezt nun, die Flügel seyen unter dem
Winkel C₄ = 14° gestellt, so wird sich das
Rad um die Streke DE, d.h. um 1/4 seines Umfanges
drehen, während diese Drehung bei einem Winkel C₃
= 26 2/3° doppelt so groß oder gleich DF,
bei einem Winkel C₂ = 45° das Vierfache
oder gleich DG seyn wird. Oder, um diese Resultate
im Zeitmaaße auszudrüken, ein Rad, dessen Flügel einen Winkel C₄ = 14° bilden, wird in derselben Zeit vier Umdrehungen
machen, in welcher es zwei Umdrehungen vollendet, wenn die Flügel einen Winkel von
26 2/3, oder eine Umdrehung, wenn die Flügel einen Winkel von 45° bilden. Ist
der Winkel bei C₄ = 14°, so muß zur
Erzeugung einer Umdrehung begreiflicher Weise eine Wassermenge gleich dem Inhalte
eines Cylinders von dem Durchmesser des Rades und der Tiefe ED durch das Rad gehen; der Winkel FCD würde die doppelte Quantität Wasser zu einer
Umdrehung erfordern.
Folgende Tabelle zeigt den Unterschied zwischen den Flügeln einer Windmühle mit
gewöhnlicher Winkelstellung und den nach Hrn. Biram's
Methode angeordneten Flügeln, deren Krümmung die oben erwähnten, stufenweise
abnehmenden Winkel darbietet. Hiebei ist angenommen, daß der Halbmesser in sechs
gleiche Theile getheilt sey, und daß der Flügel an seinem äußersten Ende einen
Winkel von 7° mit der Ebene der Bewegung bilde.
Aeußerstes Ende
Theilungspunkte des Halbmessers
1
2
3
4
5
6
Winkelnach der gewöhnlichen Methode
18°
19°
18°
16°
12 1/2°
7°
Winkel nach Biram's System
37 1/2°
20 1/2°
14°
10 1/2°
8 1/2°
7°
Eine bequeme Methode, die den Schaufeln oder Flügeln zu gebenden Winkel in jedem
beliebigen Abstande von dem Mittelpunkt zu ermitteln, wenn ein Winkel in beliebigem
Abstande gegeben ist, findet man in Fig. 35 dargestellt.
Unter der Linie BC stelle man sich die
Centrallinie, unter DE den Umfang des Rades vor;
Cb, Cc, Cd, Ce, C
f sind radiale Linien, welche mit CD beziehungsweise die Winkel von 14°2',
26°34', 45°, 56°19', 63°26' bilden; g, h, i, k, l, m, n, o, p, q, r, s, t, u andere schiefe
Linien, deren respective Winkel mit CD in der
Figur gleichfalls näher bezeichnet sind; 1, 2, 3, 4, 5 Verticallinien, parallel zu
der Centrallinie, welche die verschiedenen schiefen Linien in gleichen Abständen von
der Centrallinie durchschneiden. Der Winkel nun, welchen ein Flügel mit irgend einem
gegebenen Endwinkel an irgend einer dem Mittelpunkte näher gelegenen Stelle z.B. 5,
4, 3, 2, 1 bilden soll, ist gleich dem Winkel, den die schiefe Linie mit der einen
oder der andern an dieser Stelle sie durchschneidenden Verticallinie 5, 4, 3, 2, 1
bildet. So bildet z.B. ein Flügel, dessen äußerstes Ende unter einem Winkel von
45° gestellt ist, bei den bezeichneten Abständen vom Mittelpunkte des Rades
folgende Winkel:
Abstand.
Winkel.
1/6
80° 32'
2/6
71° 34'
3/6
63° 26'
4/6
56° 19'
5/6
50° 11'
Daß diese Winkel in der That diejenigen sind, welche den besten praktischen Effect
liefern, läßt sich auf folgende Weise erläutern. Mit Bezug auf Fig. 35 wird man
bemerken, daß die 45° geneigte Linie Cd
beide über ihr befindliche Radiuslinien c und b, welche die Basislinien zu den Winkeln von
beziehungsweise 26°34' und 14° 2' bilden, durchschneidet und zwar die
eine in ihrer Mitte, die andere in 1/4 ihrer Länge vom Mittelpunkte aus gerechnet.
Hieraus folgt, daß ein an seinem Ende 45° schief gestellter Flügel oder
deßgleichen eine Schaufel, wenn sie die Hälfte des Durchmessers einer 26°34'
oder 1/4 des Durchmessers einer 14°2' schief gestellten Schaufel zum
Durchmesser besizt, während einer Umdrehung dieselbe Streke wie jede der beiden
andern durchlaufen muß. Und was von dem einen Winkel gilt, gilt auch von allen
andern, so daß sich hieraus folgende allgemein anwendbare Regel herleiten läßt, um
den Winkel eines Flügels oder einer Schaufel in einem beliebigen Abstande auf dem
Halbmesser zu finden, wenn ein Winkel in irgend einem andern Abstande gegeben
ist.
Von dem Punkte C auf der Radiuslinie Ca aus trage man den gegebenen Distanzwinkel ab
und ziehe von der gegebenen Distanz aus eine Linie parallel zu CB, dann durch den Distanzwinkel eine andere
schiefe Linie, bis sie die erwähnte Parallellinie durchschneidet, und fälle von dem
Durchschnittspunkte ein Perpendikel auf die Linie CB. Die durch dieses Perpendikel auf der Linie CB abgeschnittene Linie dividirt durch den
radialen Abstand, ist die Tangente des gesuchten Winkels, woraus sich mit Hülfe der
trigonometrischen Tabellen leicht der Winkel selbst bestimmen läßt. Man nehme z.B.
den Durchschnitt der horizontalen Linie 9 mit der Verticallinie 3, so ist 9/3 = 3
nahe die Tangente des Winkels 71° 34'. Hr. Biram
führt ein sehr einfaches und interessantes Experiment an, mit dessen Hülfe man sich
durch den Augenschein überzeugen kann, daß Flügel oder Schaufeln, die nach obigem
Principe gekrümmt sind, einen weit größern Effect, als alle andern liefern. Man
streue auf die Wasseroberfläche eines Gefäßes von hinreichendem Rauminhalt kleine
Papierschnizel oder andere leichte Körperchen und tauche das Modell eines obigen
Verbesserungen gemäß construirten Rades in das Wasser und bewege das Rad in der
Richtung seiner Achse vorwärts. Das Rad wird sich alsdann frei drehen, ohne jedoch
das Wasser oder die auf demselben schwimwenden Körperchen merklich aufzuregen; nur die mit den Kanten des
Rades in unmittelbare Berührung kommenden Theilchen werden in Bewegung gerathen,
woraus deutlich hervorgeht, daß das Wasser eine rotirende Bewegung erzeugt, ohne
selbst im geringsten eine Störung seines Gleichgewichts zu erleiden. Nun mache man
denselben Versuch mit dem Modell eines nach dem gewöhnlichen System construirten
Rades mit ebenen Schaufeln, so wird man bemerken, wie sich das Wasser an der
Vorderseite des Rades mehr oder weniger aufstaucht und die schwimmenden Theilchen
mehr oder weniger in Bewegung gerathen, zum augenscheinlichen Beweis, daß eine von
der vorgeschriebenen Methode abweichende Form und Stellung der Schaufeln dem
Durchgang des Wassers ein unnöthiges Hinderniß in den Weg gelegt hat.
Bei Maschinen, welche auf Wasser oder Luft wirken, und ihre Bewegung aus irgend einer
andern Quelle, z.B. vom Dampfe oder thierischer Kraft herleiten, ist ein anderes
Princip als das im Vorhergehenden erläuterte vorherrschend. Biram untersucht zunächst solche Treibapparate, welche am Stern des
Schiffes angebracht werden und in einer zum Lauf des Schiffs senkrechten Ebene
rotiren. Hier kann man mit Bezug auf die Figuren 33 und 34 annehmen,
daß die durch eine Umdrehung des Rades hervorgebrachte Wirkung mit dem Winkel
wächst, welchen die Schaufeln mit der Ebene der Bewegung bilden, jedoch nur zwischen
gewissen Gränzen; denn wenn die Schaufeln des Rades W
einen Winkel von 56 1/3° bilden, so geht während einer Umdrehung ein
Luft- oder Wassercylinder von der Tiefe HD
durch dieselben, während bei einem Winkel von 45° die Tiefe der genannten
Säule nur GD, oder der Höhe des Radumfanges
gleichkommt. Das Resultat mehrerer Versuche, die mit solchen Treibapparaten, welche
am Stern des Schiffes ganz unter Wasser getaucht waren, angestellt wurden, zeigte,
daß sie dieselbe Wirkung wie gewöhnliche Schaufelräder von größerm Durchmesser
äußern, zugleich aber vor jenen den Vortheil voraus haben, daß sie unter Wasser
arbeiten und an einer Stelle des Schiffs, wo sie dessen Lauf nicht hindern. Außerdem
ist jene bei Dampfbooten öfters so lästig fallende zitternde Bewegung durch die
schiefe Lage, unter welcher die Schaufeln ins Wasser treten und durch die
verminderte Anzahl derselben beinahe ganz beseitigt.
Die Figuren 28
und 29
liefern die Seiten- und Endansichten eines an der Seite eines Dampfboots
anzubringenden Schaufelrades, bei dessen Construction die oben erläuterten
Bedingungen beobachtet sind.
A, A sind zwei parallele Metallgestelle, jedes mit sechs
Speichen und zwei
concentrischen Kränzen. Die Speichen beider Gestelle liegen zwar in parallelen
Ebenen, sind jedoch nicht selbst einander parallel; diejenigen auf der
entgegengesezten Seite des Rades sind mit a, a
bezeichnet. B, B sind sechs zwischen den concentrischen
Kränzen an die Gestelle geschraubte oder genietete Seitenplatten. C, C sind die in diagonaler Richtung quer über das Rad
gehenden Schaufeln, deren äußere Kanten mit der Seite des Rades einen Winkel von
45°, deren innere Kanten einen Winkel von ungefähr 68° bilden. Fig. 30 und
Fig.
30ª sind Skizzen in der Seiten- und Endansicht, welche einen
deutlichen Begriff von der Schaufelform dieses Rades geben mögen. AB stellt die äußere, CD die innere Schaufelkante dar.
Zur Ventilation der Gruben empfiehlt Hr. Biram dieselbe
Construction, welche er als Treibapparat für Schiffe für geeignet hält.
Tafeln