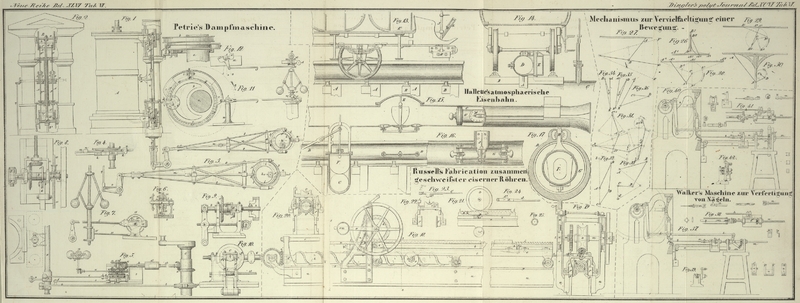
| Titel: | Mechanismus zur Vervielfältigung einer Bewegung. |
| Fundstelle: | Band 96, Jahrgang 1845, Nr. CVII., S. 428 |
| Download: | XML |
CVII.
Mechanismus zur Vervielfaͤltigung einer
Bewegung.
Aus dem Civil Engineer and Architects' Journal, März
1845, S. 69.
Mit Abbildungen auf Tab.
VI.
Mechanismus zur Vervielfältigung einer Bewegung.
Dieser Gegenstand wurde in neuerer Zeit durch die Anwendung der archimedischen Schraube zum Treiben von Dampfschiffen wieder vielfach
angeregt; sowohl durch praktische Versuche als durch mathematische Forschungen wurde
nachgewiesen, daß die Nüzlichkeit dieses Treibapparats größtentheils von der
Geschwindigkeit abhängt, womit sich die Schraube dreht. Die bis jezt gebräuchliche
Art, die hin und wiederkehrende Bewegung der Kolbenstange an einer Dampfmaschine in
eine kreisförmige umzuwandeln, besteht in der Anwendung des Krummzapfens, dessen
Umdrehungsanzahl immer gleich ist der Anzahl Doppelhube der Kolbenstange, so daß,
während leztere von ihrer niedersten Lage in ihre höchste übergeht, und von da
wieder zurük in ihre tiefste, sie eine vollkommene Umdrehung des Krummzapfens
hervorbringt. Die auf diese Weise hervorgebrachte Umdrehungsgeschwindigkeit wurde
aber zu klein befunden, als daß eine archimedische Schraube ohne Anwendung von
verzahnten Rädern oder Riemen wirksam arbeiten könnte, und leztere wurden deßhalb
angewandt, um die Umdrehungsgeschwindigkeit der Krummzapfen zu vervielfältigen. Die
Anwendung von verzahnten Rädern hat indessen manche beachtenswerthe Nachtheile; die
Reibung der Zähne an einander hat eine bedeutende Abnüzung zur Folge und die Räder
selbst greifen, wenn Abnüzung stattgefunden hat, nicht mehr gehörig in einander ein,
es kommen häufige Brüche vor, und endlich ist das Geräusch, welches sie
hervorbringen, wenn sie im Gange sind, ein Hauptgrund, weßhalb sie keine allgemeine
Anwendung fanden. Dieser lezte Nachtheil ist durch Anwendung von Rädern mit hölzernen Zähnen zum Theil
beseitigt; jedoch treten dann die ersteren beiden doppelt stark hervor.
Folgende Methode eine Bewegung bloß durch die Anwendung eines
Krummzapfen-Systems zu vervielfältigen, ist keineswegs als eine vollkommene
Lösung dieses wichtigen mechanischen Problems zu betrachten, sondern sie soll nur,
weil bis jezt noch nichts derartiges angewandt wurde, dazu beitragen, die in
Aussicht gestellte Lösung zu fördern.
Wir sagten oben, daß jeder Doppelhub der Kolbenstange bloß eine Umdrehung des Krummzapfens hervorbringe. Folgendes ist jedoch eine
Methode, mittelst welcher zwei Umdrehungen hervorgebracht werden können.
In Fig. 26
stellt A₂ das Ende einer Kolbenstange vor (die
Kolbenstange selbst ist, um Undeutlichkeit zu vermeiden, weggelassen), welches sich
in gerader Linie von A₁ bis A₄ bewegen kann. Es wird hier vorausgesezt, daß
das Kolbenstangen-Ende eine gerade Leitung oder Führung in einer Nuth oder
einem Schliz habe, wie dieß bei direct wirkenden Maschinen der Fall ist. A₃ ist die Mitte zwischen A₁ und A₄ und dieser Mitte
gegenüber liegt eine andere Nuth oder Leitung B₁
B₃ und zwar rechtwinkelig zu A₁ A₄ und
ungefähr von der halben Länge derselben. In dieser Nuth gleitet das eine Ende E einer Stange, während ihr anderes Ende mit A₂ verbunden ist. Es ist nun leicht einzusehen,
daß wenn A₂ sich von A₁ bis A₄ bewegt, B₂ von B₁ zu
B₃ geht und wieder zurük, und daß deßhalb
eine hin- und wiederkehrende Bewegung von A₂ zwei solchen Bewegungen von B₂
entspricht. Denn wenn A₂ bei A₄ ist, so hat die Stange die Lage der punktirten
Linie, und wenn sich A₂ von A₄ bis zu A₃
bewegt, so bewegt sich B₂ von seiner tiefsten bis
zu seiner höchsten Lage; B₂ geht aber wieder
abwärts, sobald A₂ den Mittelpunkt A₃ überschritten hat, und ist wieder in seiner
tiefsten Stellung, wenn A₂ zu A₁ kommt. Dasselbe geschieht, wenn A₂ wieder zurükgeht. Auf diese Weise bringt jede
vollständige Bewegung von A₂ zwei ähnliche an B₂ hervor, und wäre deßhalb ein Krummzapfen bei
B₂ angebracht, so würde derselbe sich doppelt
so oft drehen, als einer der bei A₂ angebracht
wäre.
Es ist einleuchtend, daß dieselben Mittel, durch welche die hin- und
wiederkehrende Bewegung von A₂ in eine doppelte
von B₂ verwandelt wurde, auch angewandt werden
können, um die Bewegung von B₂ noch einmal für
einen dritten, vierten etc. Krummzapfen zu verdoppeln, so daß man auf diese Weise
die Anzahl Hube einer Kolbenstange (oder Umdrehungen eines Krummzapfens) auf 2, 4,
8, 16 etc. vervielfältigen kann, oder um einen mathematischen Ausdruk zu gebrauchen, auf irgend eine
Potenz von 2. In der Praxis aber würde nach zwei oder drei Vervielfältigungen der
Mechanismus zu complicirt werden, um wirksam zu seyn; auch hängt mit demselben noch
ein anderer Uebelstand zusammen, nämlich der, daß die Größe der Bewegung von B₂ nur noch die Hälfte der Bewegung von A₂ beträgt. In der That wird sie, was man mit der
geringsten Kenntniß von Geometrie begreift, genau nur halb so groß, wenn B₁, das Ende der zweiten Führung, mit dem Punkt
A₃, der Mitte der ersten Führung,
zusammenfällt. Sollten nun mehrere solche Führungen angewandt werden, so würde die
Verminderung der Bewegung so oft wiederholt werden, daß die lezte Stange keine
hinreichend große Bewegung mehr hätte, um einen Krummzapfen treiben zu können.
Diesem Nachtheil kann jedoch abgeholfen, oder derselbe wenigstens vermindert werden.
Aus Fig. 26
ersieht man, daß es nicht absolut nothwendig ist, daß die Führung A₁ A₄
geradlinig sey. Die Wirkung würde genau dieselbe seyn, wenn die Führung ein
Kreisbogen wäre, oder was dasselbe ist, wenn A₂,
anstatt das Ende einer Kolbenstange zu seyn, das Ende eines Balanciers wäre, dessen
eines Ende sich um einen Zapfen dreht und dessen anderes sich von A₁ nach A₄ in
einem Bogen bewegt; die Bewegung der zweiten Stange bliebe dieselbe.
Die nächste Figur ist ein Beispiel hievon.
In Fig. 27 ist
nämlich der Balancier C, D, welcher sich um einen Zapfen
bei C₁ dreht, bei B
mit einer Stange verbunden, deren Ende A sich wie in
Fig. 26
in einer Führung bewegt. Die Größe der Bewegung von D
zwischen E und F₁ ist
beinahe dieselbe, wie die von A₁, und eine andere
Stange könnte nun bei D angebracht seyn, um die Bewegung
zu vervielfältigen. Auf diese Weise könnte die Bewegung einigemal vervielfältigt
werden, ohne daß ihre Ausdehnung unpassend verkleinert würde.
Diese Methode, eine abwechselnde Bewegung zu vervielfältigen, kann direct für eine
rotirende Bewegung angewandt werden, ohne daß dazwischen noch besondere
Maschinentheile nothwendig wären. Fig. 28 und 29 stellen ein
Schema dieser Art vor; A ist, wie in Fig. 26 das Ende einer
Kolbenstange, welches sich in einer Führung A₂
A₇ bewegt. (Es ist unwesentlich, ob die
Führung gradlinig ist, oder ob A sich in einem
Kreisbogen am Ende eines Balanciers bewegt.) C, der
Mittelpunkt, um welchen sich die Kurbel dreht, liegt A₅ gegenüber, was die Mitte der Bewegung von A ist. Fig. 28 und 29 zeigen den Krummzapfen
in verschiedenen Stellungen, indem in beiden Figuren gleiche Buchstaben dieselben
Gegenstände bezeichnen. A₁ B₁ ist
die Stange, welche den Krummzapfen mit A verbindet. Es
soll nun der Gang des Krummzapfens beschrieben werden, indem wir abwechslungsweise
auf beide Figuren hinweisen.
Der Krummzapfen und die Zugstange haben zuerst die Lage A₁ B₁ C₁, Fig. 28; der Krummzapfen bewege sich in der Richtung des Pfeils, und A₁ gegen A₂.
Sobald A₁ mit A₂ zusammenfällt, ist die Lage des Krummzapfens und der Zugstange die
der punktirten Linie A₂ B₂ C₄ und Krummzapfen und
Zugstange liegen in gerader Linie. Das Moment des Krummzapfens wird denselben noch
fortbewegen, und da A₁ nun von A₂ zurükgeht, so wird der Krummzapfen, wenn A₁ zu A₃
kommt, in der Stellung B₃ C₁ seyn. Die nächste Stellung ist dann A₄ B₄ C₁, Fig. 29, und die darauf
folgende B₅ A₅
C₁, so daß Zugstange und Krummzapfen
übereinander zu liegen kommen. Die folgende Stellung ist A₆ B₆ C₁, und bevor A₁ den Punkt A₇ erreicht hat, wird der Krummzapfen eine ganze
Umdrehung vollendet haben. Es wird nun nicht nöthig seyn, die Bewegung zu
beschreiben, nachdem die Theile die Lage A₇ B₇ C₁ erlangt
haben; denn man sieht leicht ein, daß wenn A₁
zurükgeht, die Bewegung wie zuvor fortgesezt wird, und daß, wenn A₁ wieder bei A₂ eingetroffen ist, der Krummzapfen und die Zugstange wieder die Lage
A₂ B₂ C₁ haben werden, und daß dadurch also die zweite
Umdrehung vollendet seyn wird. Eine vollständige hin- und wiederkehrende
Bewegung von A wird also zwei Umdrehungen des
Krummzapfens entsprechen.
Der einzige Unterschied zwischen diesem Krummzapfen und dem jezt gebräuchlichen
besteht in ihrer Lage. Bei dem neuen liegt der Drehungsmittelpunkt der Mitte der
Bahn von A gegenüber, bei dem gewöhnlichen liegt er in
der Fortsezung der geraden Linie, in welcher sich A
bewegt, und deßhalb hat auch jeder Kolbenhub nur eine
Umdrehung zur Folge.
Fig. 30 ist
eine Combination der in Fig. 28 und 29 und in Fig. 26
angedeuteten Ideen; in diesem Fall wird die Bewegung vervierfacht, denn bei jeder
abwechselnden Bewegung von A in seiner Führung wird B in der seinigen zweimal hin- und herbewegt, und
da bei jedem Laufe von B der Krummzapfen C, D sich zweimal dreht, so bringt jeder Hub von A eine viermalige Drehung der Kurbel hervor.
Wir sagten oben, daß es unwesentlich ist, ob die abwechselnde Bewegung in einer
geraden Führung stattfinde, oder ob sie die kreisförmige eines Balanciers sey;
entweder kann jede Weise für sich stattfinden, oder beide können auf irgend eine
passende Art mit einander verbunden werden. Fig. 31 ist ein Fall, wo
keine Führungen angewandt wurden, und wobei achtfache Bewegung stattfindet. Man darf nicht befürchten,
daß der Mechanismus complicirt wird, weil so viele Linien in der Figur sind; die
schwarzen Linien allein stellen die ganze Maschinerie dar; die punktirten Linien
zeigen bloß die äußersten Lagen der beweglichen Theile an.
A₁ C₁ ist der
erste bewegliche Balancier, welcher um den Zapfen C
schwingt. Bei jeder Oscillation von A₁ oscillirt
der Punkt A₂ auf dem Balancier A₂ C₂ zweimal
nach der punktirten Linie, in Folge der Verbindung durch die Stange A₁ A₂; ebenso
wird bei jeder Oscillation des zweiten Balanciers der Balancier A₃ C₃ zweimal
oscilliren, und aus dem Vorhergehenden ist klar, daß für jede Schwingung des dritten
Balanciers die Kurbel D, E sich zweimal drehen wird. Die
Bewegung ist daher achtmal vervielfältigt.
Nachdem wir nun verschiedene Arten betrachtet haben, wie abwechselnde Bewegungen
vervielfältigt in kreisförmige verwandelt werden können, gehen wir zu einem
Verfahren über, wodurch kreisförmig fortlaufende Bewegungen in vervielfältigte
kreisförmig fortlaufende Bewegungen umgesezt werden können. Dieß ist sehr einfach:
A, B, Fig. 32, ist eine Kurbel,
welche sich um A dreht, und durch eine Stange B, D, von derselben Länge wie A,
B mit einer kleineren Kurbel C, D verbunden
ist, die nur zwei Drittel oder die Hälfte der Länge von AB hat. CD dreht sich um C₁ und die Entfernung AC = CD. Bei
jeder Umdrehung von AB wird sich nun CD zweimal drehen. Es ist schwierig dieß durch
eine Skizze zu erklären; will aber der Leser seinen Scharfsinn durch Zeichnen der
verschiedenen Stellungen der beiden Krummzapfen in obigen Figuren üben, so wird er
sich von der Wahrheit überzeugen. Dieselben Buchstaben bezeichnen denselben
Gegenstand in allen fünf Figuren, und von den Kurbeln wird vorausgesezt, daß sie
sich, wie die Zeiger einer Uhr, in derselben Richtung drehen. In Fig. 32 hat AB gerade seine höchste Stellung verlassen und
beginnt sich abwärts zu bewegen; dasselbe ist bei CD der Fall (wenn AB mit der punktirten
Linie Ab zusammenfällt, so liegt CD in CA). In
Fig. 33
ist AB noch abwärts gehend und CD ebenfalls, bis es seine tiefste Stellung Cd angenommen hat, worauf es wieder steigt,
obgleich AB nach abwärts geht. In Fig. 34 ist AB noch nicht in seiner tiefsten Stellung und CD ist noch nicht bis in seine höchste Stellung
gestiegen; sobald AB seine tiefste Stellung
erreicht hat, hat CD eine Umdrehung vollendet,
während AB doch nur eine halbe gemacht hat. In
Fig. 35
beginnt AB eben wieder zu steigen und CD fängt seine zweite Umdrehung an. In Fig. 36 ist
AB ein wenig mehr gestiegen und CD hat eine Viertelumdrehung gemacht.
Es ist nun nicht nothwendig, die Bewegung weiter zu verfolgen; der Lauf von AB bei seinem Emporsteigen ist derselbe, wie beim
Abwärtsgehen, nur wird CD angezogen anstatt
geschoben; so bald nun AB seine höchste Stellung
erreicht hat, hat auch CD zwei Umdrehungen
vollendet.
Dieß ist vielleicht die passendste Art, eine Bewegung zu vervielfältigen. Die Achse
der zweiten Kurbel C, D könnte noch eine andere, die der
A, B gleich wäre, tragen, wodurch eine nochmalige
Verdoppelung der Bewegung, wie die erste war, hervorgebracht würde. Eine dritte
Verdoppelung könnte nun noch aus der zweiten hervorgehen, und so fort. Zu bemerken
ist noch, daß eine Vereinigung der in den lezten fünf Figuren dargestellten Methode
mit derjenigen Fig.
30 leicht die ursprüngliche Bewegung verachtfachen könnte.
Durch die angeführten Methoden könnte man in vielen Fällen eine Bewegung hinlänglich
vervielfältigen, ohne daß sie die Einwürfe treffen, welche den verzahnten Rädern
gemacht werden. Schließlich mag noch bemerkt werden, daß die hier beschriebenen
Mechanismen keinen KraftverlustDurch die viele Reibung und den oft bedeutenden Seitendruk möchte doch wohl
Kraftverlust stattfinden. Ferner wird die kreisförmige Bewegung durchaus
nicht gleichförmig, indem die Krummzapfen in gleichen Zeiten ungleiche
Winkel durchlaufen, was aus Fig. 28 recht
deutlich zu sehen ist. Während A von A₂ zu A₇ geht, macht der Krummzapfen mehr als 1 1/3 Umdrehungen, und
während A von A₇ wieder zurük zu A₂ geht,
nur noch 2/3. Schwungräder würden wahrscheinlich für jede Verdoppelung nach
Fig.
32 bis 36 sehr
nothwendig seyn.Walther. hervorbringen; dieß könnte für jeden einzelnen Fall bewiesen werden, aber es
wird genügen an den bekannten mechanischen Grundsaz zu erinnern, daß die Zunahme der
Geschwindigkeit die Veränderung der Kraft ausgleicht.
Die Anzahl der Umdrehungen einer Dampfmaschinenachse wird gewöhnlich durch Zahnräder
vervier- oder verfünffacht, wenn eine archimedische Schraube getrieben werden
soll.
Tafeln