| Titel: | Ueber den Reichenbach'schen Distanzmesser; von Professor G. Decher. |
| Autor: | Georg Decher [GND] |
| Fundstelle: | Band 116, Jahrgang 1850, Nr. IX., S. 29 |
| Download: | XML |
IX.
Ueber den Reichenbach'schen Distanzmesser; von Professor
G. Decher.
Mit Abbildungen auf Tab.
I.
Decher, über den Reichenbach'schen Distanzmesser.
Der Bericht über die Meßinstrumente des Hrn. Dr. Romershausen zu Halle (im polytechn. Journal Bd. CXIV S. 34) veranlaßt mich, diesen
Instrumenten gegenüber die Ehre des Reichenbach'schen Distanzmessers zu retten, von welchem Hr. Dr. August Wiegand zu Halle
in einer Lobrede auf die genannten Instrumente in Grunert's Archiv Bd. XIII Heft 2 meint, er sey
praktisch durchaus unbrauchbar.
Der Reichenbach'sche Distanzmesser steht keinem andern ähnlichen Instrumente in der Einfachheit
seiner Einrichtung und seiner Behandlung nach, übertrifft aber alle bis jetzt
bekannten, namentlich in solcher Weise angewendet, wie ich unten zeigen werde, weit
an Genauigkeit der damit erhaltenen Ergebnisse; denn er gibt die Entfernungen einer
richtig getheilten Latte von dem Instrumente sehr leicht auf 1/500 derselben durch
unmittelbares Ablesen, und zwar bei 25 bis 30maliger Vergrößerung des Fernrohres von
100' und selbst von 50' an bis 1000', eine Genauigkeit, welche mit dem Längenmesser (Diastimeter) von Dr. Romershausen bei weitem nicht erreicht
werden kann; denn – zugegeben, daß dieses Instrument, wie behauptet wird, die
Parallaxe des anvisirten Objects auf Secunden genau angibt – für ein Object
von 15 Fuß und eine Entfernung von 300' muß das Instrument 1',5 lang seyn, wenn die
Entfernung der Stahlspitzen 1'' betragen soll; ein Fehler von 1 Secunde entspricht
dann einem Fehler von 0'',015 im Einstellen der Stahlspitzen und demnach einem
Fehler von 15/1000 oder 1 1/2 Proc. der gemessenen Entfernung; und die Unsicherheit
der Messung wäre über 7mal so groß als bei dem Reichenbach'schen Distanzmesser. Dabei gibt letzteres Instrument zugleich
die Elevations- und Depressionswinkel für die geneigten Linien, und mittelst
einer Reductionstabelle können deren Horizontal-Projectionen ungleich genauer
und schneller gefunden werden, als dieß durch das sogenannte Reductionsniveau von Dr. Romershausen möglich ist.
Leider scheint der Reichenbach'sche Distanzmesser, welcher
richtig angewendet für die Detailvermessung auf gebirgigem Boden, sowohl bei der Aufnahme mit dem
Meßtische, als bei der polygonometrischen Vermessung, eine sehr große Ersparniß an
Zeit und Mühe gewährt, den meisten Verfassern von Lehrbüchern der praktischen
Geometrie nur dem Namen und dem Principe nach bekannt zu seyn; er findet sich
wenigstens meistens nur oberflächlich erwähnt und beschrieben; von einer genaueren
Theorie desselben, nach welcher die Theilung der Latte und die Tabelle für die
Reduction geneigter Linien auf den Horizont berechnet werden kann, ist nirgends die
Rede. Am ausführlichsten scheint derselbe in dem „Handbuch der Meßkunde von Dr. Barfuß“ abgehandelt zu seyn; der Verfasser
kennt aber auch nur eine empirische Theilung der Latte, und die Messung schiefer
Linien ist bei ihm mit Umständlichkeiten verbunden, wodurch dieselbe viel an
Sicherheit verliert. Wahrscheinlich hat auch Hr. Dr. Wiegand sein Urtheil an dieser Quelle geschöpft. Es
dürfte deßhalb nicht überflüssig seyn, eine genaue Theorie unseres Distanzmessers,
nach welcher ich schon für sechs verschiedene Instrumente die Theilung der Latten
sowie die erforderlichen Reductionstabellen ohne einen andern vorausgehenden
Versuch, als die Bestimmung der Brennweite des Objectives berechnet habe, nebst
einigen zweckmäßigeren Einrichtungen der Latte, als die bisher gebräuchlichen,
bekannt zu machen, da ich mich selbst durch mehrfachen Gebrauch jener Instrumente
von der Richtigkeit dieser Rechnungen und der Sicherheit der damit vorgenommenen
Messungen innerhalb der angegebenen Gränze überzeugt habe.
Der Reichenbach'sche Distanzmesser besteht im Wesentlichen
aus einem guten achromatischen Fernrohr, das mittelst eines Stativs fest aufgestellt
und um eine horizontal gerichtete Achse gedreht werden kann; zur Bestimmung der
Neigung der optischen Achse des Fernrohres gegen den Horizont ist dasselbe mit einem
verticalen Gradbogen und zum genauen Einstellen mit einer Mikrometerbewegung
versehen. Vor dem Oculare desselben sind zwei horizontale Fäden so angebracht, daß
deren gegenseitige Entfernung durch Schrauben, denen eine Feder entgegenwirkt,
vergrößert oder verkleinert, und ihnen dabei eine gleiche Entfernung von der
optischen Achse des Fernrohres gegeben werden kann. Diese Einrichtung läßt sich
demnach mit jedem Meßinstrument, mit der Kippregel wie mit dem Theodolit und dem
Nivellirinstrument einfach dadurch verbinden, daß man dem gewöhnlichen Fadenkreuze
vor dem Ocular des Fernrohrs dieser Instrumente noch die beiden horizontalen Fäden
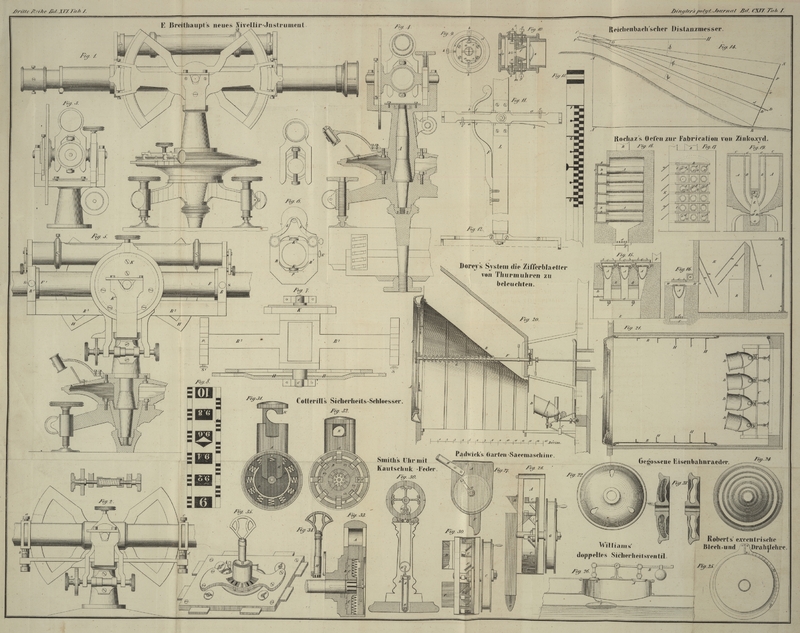
beifügt. In Fig.
9 und 10 ist ein solcher Ocularkopf für einen kleinen Theodoliten von vorn nach
Wegnahme der Ocularlinse und im Durchschnitt dargestellt; a,
a sind zwei prismatische Schieber, auf deren Rückseite vom Ocular aus
angesehen, die horizontalen Fäden zur Distanzmessung aufgespannt sind, und die durch die
Schrauben b, b, denen die Feder e entgegendrückt, in die gehörige Stellung gebracht werden können; die
Köpfe dieser Schrauben sind außen durch einen Ring d vor
einer zufälligen Drehung geschützt. Der conische Körper f trägt auf seiner dem Ocular zugewendeten Stirnfläche, also in der Ebene
lm, in welcher auch die Fäden für die
Distanzmessung liegen, das rechtwinkelige Fadenkreuz, oder was für die Winkelmessung
viel zweckmäßiger ist, außer dem die optische Achse schneidenden horizontalen Faden,
zwei sehr nahe liegende parallele Verticalfäden,
zwischen welche das Object viel genauer eingestellt werden kann, als es mittelst eines Fadens oder gekreuzter Fäden möglich ist; vier
Schrauben g dienen zum Centriren des Fadenkreuzes. Die
Schraube h hält den Ring i,
in welchem das Fadennetz befestigt ist, in seiner dem Auge des Beobachters
entsprechenden Stellung in Bezug auf das Ocular o fest,
und es ist eben sowohl für die Distanzmessung als für die Winkelmessung auf diese
Stellung eine besondere Sorgfalt zu verwenden. – Für stärkere Fernröhren und
mit einer größeren Distanz der Horizontalfäden, wie sie bei der bayerischen
Katastervermessung in Verbindung mit der Kippregel gebraucht wurden, ist es für das
richtige Ablesen besser, wenn vor jedem der beiden Horizontalfäden eine besondere
Ocularlinse angebracht wird; es hat dann das ungenaue Einstellen des Oculars oder
vielmehr der Fäden in Bezug auf das Bild der Latte einen weniger bedeutenden
Einfluß, als wenn beide Fäden durch eine und dieselbe Ocularlinse betrachtet
werden.
Dieses Instrument wird mit seiner Drehungsachse C, Fig. 14,
lothrecht über dem Anfangspunkt A der zu messenden Linie
aufgestellt, und ihm gegenüber am Endpunkte B derselben
die Distanzlatte BN
von dem Meßgehülfen in einer solchen Lage gehalten, daß das darauf senkrecht
stehende Visir oder Diopter Dd auf das Objectiv
O des Fernrohrs gerichtet ist, die Latte also auf
der Verbindungslinie OD senkrecht steht. Diese
Latte besitzt eine entsprechende Theilung, deren Nullpunkt am besten oben angebracht
wird, damit derselbe einestheils nicht so leicht durch Gebüsch, Getreide etc.
verdeckt wird, theils weil die Luft in einiger Höhe über dem Boden immer ruhiger
ist, als in der Nähe desselben, während die zu messenden Linien selten die größte
Länge, für welche die Latte ausreicht, besitzen, und demnach in den meisten Fällen
mit beiden Fäden in der ruhigeren Luft abgelesen werden kann. Ferner wird der
Nullpunkt am zweckmäßigsten durch die feine Mittellinie eines oben und unten schwarz
eingefaßten weißen Streifens gebildet, da auf diese Mittellinie, auch wenn sie gar
nicht mehr sichtbar ist, der entsprechende Horizontalfaden (der untere) selbst mit
einem wenig geübten Augenmaaße mit größter Schärfe eingestellt werden kann. Die Theilung selbst
dagegen, welche an dem oberen der beiden Distanzfäden des Fernrohrs abgelesen, die
senkrechte Entfernung der Latte von der Drehungsachse des Fernrohrs, also die Länge
der Senkrechten CD' angibt, besteht wie die
Theilung der Nivellirlatten, aus versetzten schwarzen und weißen Feldern, welche
aber höchstens 1 Zoll oder 2,5 Centim. Länge erhalten dürfen, damit sie noch durch
das Augenmaaß leicht in 10 gleiche Theile getheilt werden können; übrigens dürfen
sie auch nicht so klein gemacht werden, daß sie der Faden bei der größten Entfernung
der Latte ganz bedeckt. In Fig. 13 ist eine solche
Theilung dargestellt; jeder einzelne Theil entspricht hier einem Meter Entfernung,
und die angeschriebenen Ziffern 1, 2, 4 bedeuten Zehner von Metern, nämlich 10
Meter, 20 Meter, 40 Meter etc.
Am untern Ende ist die Latte mit einer eisernen Spitze versehen, um diese in den
Boden eindrücken, und die Latte auch in einer nicht verticalen Stellung sicher
halten zu können, was für einen festen Mann mit einigen durch die Uebung erlangten
Vortheilen in der Stellung des Körpers und namentlich in der Haltung der Arme, keine
so gar schwere Aufgabe ist, wenn die zu messende Linie sich nicht über 30°
gegen den Horizont neigt, ein Fall, der selten vorkommt und für den auch das
Fernrohr kaum mehr anwendbar ist.
Um endlich auch dem Diopter eine richtige und unwandelbare senkrechte Stellung zur
Latte zu sichern, habe ich demselben die in Fig. 11 und 12
dargestellte Einrichtung gegeben. Es dreht sich dasselbe nämlich auf einem auf der
schmalen Seite der Latte L angeschraubten conischen
Zapfen, auf dem es mittelst einer Mutter und Vorlegplatte so festgehalten wird, daß
es keine wankende Bewegung machen kann. Auf den schmalen Kanten sind zwei Federn a und b angeschraubt, eine
stärkere a, welche durch eine Schraube c in einer bestimmten Lage erhalten wird, und eine
schwächere freispielende b. Beim Richten des Diopters
legen sich diese Federn in den entsprechenden Einschnitt ef der großen an der vordern Fläche der Latte
angeschraubten Schnappfeder F ein, und geben dem Diopter
immer dieselbe Lage in Bezug auf die Latte, so daß dasselbe immer senkrecht darauf
stehen wird, wenn die Feder a einmal mittelst der
Schraube c für diesen Zweck richtig gestellt ist. In
unserer Darstellung ist auf den Fall Rücksicht genommen, wo die Latte auf beiden
Seiten zum Distanzmessen gebraucht wird, das Diopter also vorwärts und rückwärts muß
eingelegt werden können, wenn man nicht vorzieht zwei Dioptern anzubringen, damit
der Gehülfe für jede Seite der Latte, die er dem Instrumente zuwendet, das Diopter in derselben Lage vor sich
hat.
Zur Berechnung der Theilung der Latte und der Reduction der gemessenen geneigten
Linien auf den Horizont sey nun allgemein (Fig. 14):
die horizontale Distanz A
'B der Stationspunkte A und B
= d
die Entfernung CB der
Drehungsachse des Fernrohrs
vom Fußpunkt
B der Latte BN
= d₁
die senkrechte Entfernung CD' der Drehungsachse von
der Latte
oder die abgelesene Distanz
= d₂
die senkrechte Entfernung OD des Objectivs von der Latte
= d₃
die Entfernung OC des
Objectivs vom Drehungspunkt
= b
die Entfernung ON des
Objectivs vom Nullpunkt der Latte
= d₄
die Brennweite des Objectivs
= f
der Abstand des Bildes der Latte vom Objectiv
(Sammelweite)
= a
der halbe Abstand der beiden Distanzfäden f und f'
=e
der Abstand DN des Diopters
der Latte vom Nullpunkt
= L
der Abstand DB desselben
vom Fußpunkt der Latte
= l
die Länge des zwischen den Visirstrahlen ON und Ox liegenden
Theiles der Latte
= x
der Winkel zwischen der optischen Achse COP des
Fernrohrs und
der Senkrechten OD
= φ
der Winkel zwischen der optischen Achse und jeder der
Visirlinien ON und Ox oder Of und Of'
= α
der am Instrumente abgelesene
Winkel zwischen
der optischen
Achse und dem Horizont, der für die Depression positiv, für die Elevation
negativ genommen werde
= δ
endlich der Winkel, den die Senkrechte CD' mit der
Geraden CB bildet
= ψ.
Zuerst kann man wegen der Kleinheit des Winkels φ
und der Länge b im Verhältnisse zu d₂ die beiden Senkrechten CD
' und OD mit hinreichender
Genauigkeit der Richtung nach als congruent annehmen, und hat dadurch:
1) d₃ = d₂ – b;
ferner gibt das Dreieck ODN:
2) tang (φ + α) = L/d₃, 3) 1/d₄ = cos (φ + α)/d₃,
und die bekannte Formel der Dioptrik:
4) 1/a = 1/f – 1/d₄
bestimmt die Entfernung a, in
welcher das Bild des Nullpunktes der Latte vom Objectiv erscheint; man zieht
daraus
5) sin α = e/a
und kennt nun, wenn e als gegeben
vorausgesetzt wird, damit und durch das Vorhergehende, die Winkel α und φ, und
zuletzt findet man
x = L
– d₃ tang (φ – α)
= d₃ (tang (φ + α)
– tang (φ
– α))
oder sehr nahe
6) x = 2 d₃ tang α/cos²φ,
als Länge des der Distanz d₂ entsprechenden Theiles der Latte. Mittelst dieser Gleichungen können
also die Theile der Latte für verschiedene Entfernungen berechnet werden, und wenn
diese auf die Latte aufgetragen sind, kann man die Unterschiede derselben, ihrer
geringen Veränderlichkeit wegen, proportional in kleinere Theile abtheilen.
Zuvor müssen wir aber noch den halben Abstand der Distanzfäden genau bestimmen. Dieß
geschieht dadurch, daß man nach einer einfachen Proportion die Höhe H der Latte feststellt, welche dem am Instrumente
abgemessenen mittleren Abstande der Fäden und einer größten Entfernung D₂ der Latte vom Instrumente entspricht oder
entsprechen soll, und darnach die Größe e berechnet.
Bezeichnen wir dazu die Größen, welche in der Entfernung D₂ den Größen d₃, d₄, α, φ,
a und x entsprechen, mit D₃, D₄, α₁, φ₁, A und H, so haben wir wie
vorher:
D₃ = D₂ – b,
tang (α₁ + φ₁) = L/D₃, tang (α₁
– φ₁) = (H – L)/D₃
und finden daraus α₁
nach der bekannten Formel:
α₁ = 1/2 (α₁ + φ₁) + 1/2 (α₁ –
φ₁).
Es ist ferner
1/D₄ = cos (φ₁ + α₁)/D₃,
womit sich
1/A = 1/f
– 1/D₄
und zuletzt der gesuchte halbe Abstand der Fäden
e = A sin
α₁
berechnen läßt.
Ist dann die Latte auf diese Weise getheilt, so gibt man den Distanzfäden den eben
berechneten Abstand, indem man auf einem möglichst ebenen und wenig geneigten Boden
die Entfernung D₂ mit der Kette abmißt, am
Anfangspunkt das Instrument, am Endpunkt die Latte aufstellt, und die Lage der Fäden
mittelst der Druckschrauben so corrigirt, bis sie gleichzeitig auf den Punkten N und H einstehen. Um sich
dann zu überzeugen, ob die Fäden gleichweit von der optischen Achse abstehen,
bemerkt man sich die Stellung des Instrumentes am Verticalkreise und schlägt das
Fernrohr um, so daß der obere Faden der untere, der untere der obere wird, stellt
wieder auf die Latte ein, und sieht zu, ob der Gradbogen dieselbe Abweichung vom
Horizont angibt. Ist dieß nicht der Fall, so halbirt man den Unterschied, und
corrigirt die Fäden von Neuem so, daß sie die Punkte N
und H decken. Mit einem guten Augenmaaß erreicht man
übrigens denselben Zweck genauer und mit weniger Umständen. Bei dieser Correction
oder Prüfung der Distanzfäden, die nach längeren Zeiträumen immer wieder vorgenommen
werden muß, kann man sich zugleich von der Richtigkeit der Theilung der Latte
überzeugen und im Ablesen einüben, indem man beim Abmessen der Länge D₂ in mehreren Zwischenräumen Zeichen einstecken
und die entsprechenden Entfernungen notiren, und dann, wenn die Fäden corrigirt
sind, die Latte in den bezeichneten Punkten aufstellen läßt, um ihre Entfernungen
mittelst des Instrumentes zu bestimmen.
Die Reduction der abgelesenen Entfernung d₂ auf
den Horizont ergibt sich einfach wie folgt. Man hat in dem rechtwinkeligen Dreiecke
CD'B oder CDB
BD/CD =
1/d₂ = tang
ψ, CB = d₁ = d₂/cos ψ
und dann in dem Dreiecke CBA
A'B = d = d₁ cos (δ + φ + ψ)
als die gesuchte horizontale Entfernung der Stationspunkte A und B. Für die
Interpolation ist es jedoch zweckmäßiger, die an der abgelesenen Distanz d₂ anzubringende Reduction:
R = d
– d₂
zu berechnen, und diese nach den Werthen des durch die
Beobachtung gegebenen
Winkels δ in eine Tabelle, wie die unten folgende
zusammenzustellen. Man hat dann:
d = d₂ + R.
Das einfachste Mittel, sich in der Anwendung dieser Tabelle zu üben und von ihrer
Richtigkeit zu überzeugen, wird darin bestehen, das Instrument und die Latte an zwei
in verschiedener Höhe liegenden Punkten aufzustellen, und zwar zuerst das Instrument
oben, die Latte unten, und dann die Latte an der obern und das Instrument an der
untern Station, und die jedesmal abgelesenen Distanzen, die nicht gleich seyn
werden, mittelst der Tabelle auf den Horizont zu reduciren, wodurch jedesmal
dieselbe horizontale Distanz zum Vorschein kommen muß. Eine mehrmalige Wiederholung
dieses Verfahrens bei verschiedenen Entfernungen und Höhenunterschieden wird für den
Gebrauch des Instrumentes und der Tabelle der beste Lehrmeister und zugleich die
beste Empfehlung desselben seyn.
Nach der vorhergehend beschriebenen Einrichtung des Instrumentes, der Latte und
Reductionstabelle hat also der Geometer nur dafür zu sorgen:
1) daß die Distanzfäden die richtige Entfernung von einander haben;
2) daß die Drehungsachse des Fernrohrs lothrecht über dem Anfangspunkte A der zu messenden Linie, und das Instrument dabei so
aufgestellt ist, daß der verticale Kreis oder Gradbogen die Neigung der optischen
Achse gegen den Horizont richtig angibt;
3) daß die Fäden genau mit dem Bilde der Latte zusammentreffen, was man leicht durch
ein geringes Neigen des Kopfes darnach beurtheilen kann, ob die Fäden auf der Latte
unverrückt bleiben. Ist dieß nicht der Fall, so muß der Ocularkopf so lange verrückt
werden, bis es erreicht ist;
4) wenn der untere Faden auf Null eingestellt ist, so muß in demselben Augenblicke
bloß durch Verrückung des Auges mit Vermeidung jeder fühlbaren Bewegung des Körpers
auch die Stellung des obern Fadens abgelesen werden, was übrigens in kurzer Zeit
mehrmal wiederholt werden kann;
5) sogleich nachdem die abgelesene Distanz notirt, und ohne daß in der Stellung des
Instrumentes das Geringste geändert worden ist, wird die Elevation oder Depression
der optischen Achse am Gradbogen abgelesen und aufgezeichnet, und zwar genügt es,
wenn diese Winkel auf Zehntel-Grade bestimmt werden.
Der Gehülfe hat dabei nichts zu beobachten, als was früher schon erwähnt wurde,
nämlich daß die Latte in dem Endpunkte B fest
aufgestellt wird, daß das Diopter auf das Objectiv des Instrumentes zeigt, und die
schmale Seite der Latte in einer verticalen Ebene liegt. Das letztere kann übrigens
der Gehülfe nicht leicht selbst beurtheilen; es muß ihm daher von dem Geometer durch
Winken angedeutet werden. Die ganze Behandlung des Instrumentes und der Latte ist
also sehr einfach und erfordert gewiß den möglich kleinsten Zeitaufwand für die
Bestimmung der Entfernung eines Punktes aus einer
Station, wobei die Resultate hinsichtlich der Genauigkeit jede billige Anforderung
befriedigen, und namentlich den für Detailvermessungen nothwendigen Grad der
Genauigkeit selbst bei geringer Hebung des Beobachters erreichen.
Aus dem Vorhergehenden ersieht man, daß die Theilung einer Latte streng genommen für
jedes Fernrohr besonders berechnet werden muß; es geht indessen auch daraus hervor,
daß kleine Abweichungen in der Brennweite des Objectivs und in seiner Entfernung von
der Drehungsachse des Fernrohrs nur sehr kleine Aenderungen in jener Theilung
bewirken; es dürfte deßhalb für Manchen erwünscht seyn, wenn ich hier die Theilung
der Latte, sowie die Reductionstabellen für zwei verschiedene Instrumente, wie sie
meistens angewendet werden, mittheile, und bei einem derselben zugleich die Art und
Weise der Rechnung zeige.
Das erste dieser Instrumente ist ein Multiplications-Theodolit oder ein terrestrisches Universalinstrument mit einem Fernrohr zum Durchschlagen
von 12 bis 15maliger Vergrößerung; die beiden Kreise (Horizontal- und
Höhenkreis) sind nach der Centesimaltheilung in 400° und entsprechend weiter
getheilt; der Höhenkreis gibt an den Nomen Unterschiede von 5 Minuten an. Die
Brennweite f des Objectivs ist 0,2928 Meter, und der
Abstand desselben von der Drehungsachse 0,20 Meter. Die dazu gehörige Latte ist
etwas über 3 Meter lang, und nach dem metrischen Maaße getheilt, weil mir dieses für
das Ablesen die zweckmäßigste Eintheilung gab, nämlich Theile, die einer
Längeneinheit entsprechen, und nicht zu groß und nicht zu klein sind. Die Latte ist
nämlich auf der einen Seite von unten auf als Nivellirlatte in Centimeter
eingetheilt, welche bis zu Entfernungen von 50 Meter durch das Augenmaaß leicht noch
genau in 10 gleiche Theile getheilt werden können, so daß das mit einer sehr
empfindlichen Libelle versehene Fernrohr bei Stationen von 100 Meter von der Mitte
aus die Höhen auf 1 Millimeter sicher angibt. Auf der andern Seite ist die Latte als
Distanzlatte von oben herab, wie in Fig. 13 dargestellt ist, so getheilt, daß
jeder Theil, der etwa 1,5 Centim. groß ist, einem Meter Unterschied in der
Entfernung entspricht, und daß darauf die Distanzen von 10 bis 200 Meter leicht auf
1/500, und mit einiger Uebung des Beobachters, namentlich bei ruhiger Luft und guter
Beleuchtung selbst bis auf 1/1000 derselben genau abgelesen werden können.
Die Entfernung L des Diopters
dieser Latte vom Nullpunkte ist
= 1,623 Met.
„ „ l „
„ „ „
vom
Boden „
= 1,4 Met.
die Hauptdistanz D₂ zur
Correction der Fäden ist
= 200 Met.
und die entsprechende Höhe H der
Latte
= 3 Met.
Mit diesen Werthen berechnet sich zuerst der halbe Abstand der Fäden wie folgt.
Es ist:
1) D₃ = D₂
– b = 200,00 Met. – 0,20 = 199,80
Met.;
2) tang (α₁ +
φ₁) = L/D₃ = 1,623/199,80 = tang 0,5171°
3) tang (α₁
– φ₁) = (H – L)/D₃ = (3 – 1,623)/199,80 = tang
0,4387°
4) α = 1/2 (α₁ + φ₁) + 1/2 (α₁ – φ₁) = 0,4779°
5) 1/D₄ = cos (φ₁ + α₁)/D₃ = cos 0,5171/199,80 = 0,005005
6) 1/A = 1/f – 1/D₄ = 1/0,2928 – 0,005005 = 3,41029
7) e = A sin α₁
= 1/3,41029 sin 0,4779°
also:
e = 0,0022014 Met.
log e = 7,342694.
Die Berechnung der Theile der Latte, für welche es genügt, wenn sie für die
Entfernungen von 10, 20, 40, 60, 100, 150 und 200 Meter nach den obigen Formeln
durchgeführt wird, indem man damit die Werthe von x für
die dazwischen liegenden Zehner von Metern leichter durch Interpolation erhalten
kann, wird sich am einfachsten und sichersten in der nachstehenden tabellarischen
Form herstellen lassen, worin die Buchstaben d. E. decadische Ergänzung bedeuten.
Textabbildung Bd. 116, S. 39
Mit diesen Werthen ergibt sich dann durch eine leichte Interpolation die nachstehende
Tabelle für die Theilung der Distanzlatte, aus welcher man steht, wie die
Unterschiede in den Theilen allmählich mit der Entfernung zunehmen, und zwar im
Anfang sehr merklich, zuletzt aber nur sehr wenig. Man sieht ferner daraus, daß man
auch bei den kleinern Distanzen die Zwischenräume zwischen den angegebenen
Theilungspunkten in 10 gleiche Theile theilen darf, um die Theile für 1 Meter
Unterschied in der Entfernung ohne wahrnehmbaren Fehler zu erhalten.
Distanzen.
Entsprechende LängenderLatte von Null
an.
Unterschiede.
10
Met.
0,14659
Met.
20
0,29498
0,14839
30
0,44466
0,14968
40
0,59474
0,15008
50
0,74492
0,15018
60
0,89516
0,15024
70
1,04544
0,15028
80
1,19575
0,15031
90
1,34608
0,15033
100
1,49642
0,15034
110
1,64677
0,15035
120
1,79712
0,15035
130
1,94747
0,15035
140
2,09782
0,15035
150
2,24818
0,15036
160
2,39854
0,15036
170
2,54890
0,15036
180
2,69926
0,15036
190
2,84963
0,15037
200
3,00000
0,15037
Um ferner die Berechnung der Reductionstabelle in gleicher Weise durchzuführen, sucht
man zuerst den Winkel ψ und den Werth von d₁ wie folgt:
d₂ =d E. log d₂ =log l =log tang ψ
=ψ
=φ =
Met.10,009,000000,146139,14613 8°,86 9,97
Met.20,008,69897–8,84510 4°,45 4,74
Met.40,008,39794–8,54407 2°,23 2,12
Met.60,008,22185–8,36798 1°,49 1,25
Met.100,008,00000–8,14613 0°,89 0,56
Met.150,007,82391–7,97004 0°,59 0,21
Met.200,007,69897–7,84510 0°,45 0,04
φ + ψ =
18,83
9,19
4,35
2,74
1,45
0,80
0,49
d. E. log cos ψ =log d₂ =
0,004121,00000
0,001061,30103
0,000271,60206
0,000121,77815
0,000042,00000
0,000022,17609
0,000012,30103
log d₁
=
1,00412
1,30412
1,60233
1,77827
2,00004
2,17611
2,30104
und gibt der weitern Rechnung, bei welcher man sich darauf
beschränkt, die Winkel δ von 5° zu
5° zu nehmen, die nachstehende übersichtliche Einrichtung, wobei zu bemerken
ist, daß δ' für δ + φ + ψ steht.
Textabbildung Bd. 116, S. 41
Textabbildung Bd. 116, S. 42
Bezeichnet man dann die vier Werthe von R, welche
zwischen zwei in der vorstehenden Tabelle aufeinanderfolgende eingeschaltet werden
sollen, mit R', R'', R''', RIV, die letzteren selbst mit R und R₁, so hat man
nach der gewöhnlichen Interpolationsformel, indem man die dritte und die höhern
Differenzen vernachlässigt:
R' = R + 1/5
Δ R – 2/25 Δ² R,
R'' = R + 2/5
Δ R – 3/25 Δ² R,
R''' = R + 3/5 Δ R – 3/25 Δ² R,
RIV = R + 4/5 Δ R –
2/25 Δ² R,
oder für die fortgehende Berechnung zweckmäßiger:
R' = R + 1/5 Δ R – 2/25
Δ² R,
R'' = R' + 1/5 Δ R – 1/25 Δ² R,
R''' = R'' +
1/5 Δ R,
RIV = R''' + 1/5 Δ R + 1/25
Δ² R,
wozu dann das Glied
R₁ = R
IV + 1/5 Δ
R + 2/25 Δ² R
als Controle dienen wird.
Auf diese Weise erhält man die beiden Tabellen A und B, welche auf einen Streifen dünne Pappe aufgezogen, und
sogleich im Felde zur Reduction benützt werden können. In der Mitte einer jeden
derselben ist eine Spalte mit dem Kopfe: Δ
für 10 Met., welche die nahe constanten Differenzen der
in derselben Zeile stehenden Zahlen enthält (nur die beiden ersten Spalten unter 10
und 20 Met. machen davon eine fühlbare Ausnahme), und die Interpolation für die
Distanzen, welche zwischen die in der Tabelle angegebenen fallen, erleichtert. Ein
Beispiel wird die Anwendung klar machen:
Man habe auf der Latte die Distanz 113,70 Met. abgelesen bei einer Depression der
optischen Achse des Fernrohrs von 18,3°, und will dieselbe auf den Horizont
reduciren.
Die Tabelle B (Depression) gibt als Reduction für 110
Met. bei 18° Depression: 500 Met., bei 19°: 551, und demnach ist bei
18,3°
R = 500 + (551 – 500)/10 × 3 = 515
Centim.
Ferner hat
man bei
18°
für 10 Meter
die Differenz:
37
„
19°
„ „
„ „
42
–––––
also bei
18,3°
„
„ „
39
„
„
für 1 Meter
„ „
4
und „
„
für 3,7 Met.
„ „
15
Die vollständige Reduction der abgelesenen Distanz ist sonach 530 Centim. und
folglich
113,70 Met. – 5,30 Met. = 108,40 Met.
die auf den Horizont reducirte Entfernung des Stationspunktes
der Latte von der Station des Instrumentes.
Mit einiger Uebung läßt sich diese kurze Rechnung, wie dieß beim Meßtische nothwendig
ist, schon im Felde leicht und schnell ausführen; bei polygonometrischen Messungen
wird man besser thun, sich, wie schon bemerkt, die Neigungswinkel zu notiren, und
die Reduction zu Hause zu berechnen.
Das zweite Instrument, für welches hier noch die Theilung der Latte und die
Reductionstabellen folgen, ist ein Distanzmesser mit
Kippregel für die Aufnahme mittelst des Meßtisches; das Fernrohr besitzt
eine 25 bis 30malige Vergrößerung, und vor jedem Distanzfaden eine Ocularlinse; aber
kein Collectivglas. Die Brennweile des Objectivs ist = 1,675 bayer. Fuß, und der
Abstand desselben von der Drehungsachse = 0,833 Fuß. Die dazu gehörige Latte ist zum
Zusammenlegen eingerichtet, sie wird in ihrer ganzen Länge bis zu 1000 Fuß, die
Rückseite der untern Hälfte bis 500' gebraucht. Der Abstand des Diopters vom Boden
ist 4,8 Fuß; der Abstand von Null bei der ganzen (1000') Latte = 12', bei der 500'
Latte = 4'; der Hauptdistanz D₂ = 1000'
entspricht die Höhe H = 15',3. Die 1000' Latte ist in
Felder von 7''' bis 8''' Länge eingetheilt, welche einem Unterschiede von 5' in der
Entfernung entsprechen; bei der 500' Latte, die von 50' anfängt, haben die Felder
oder Theile bis zu einer Distanz von 250' nur 3''' Länge und entsprechen
Entfernungsunterschieben von 2 Fuß; von 250' bis 500' ist dagegen die Theilung auf
dieselbe Weise, wie auf der 1000' Seite beschaffen. Diese Latte hat ein Diopter wie
das in Fig.
11 und 12 dargestellte.
Mit den eben angegebenen Werthen berechnet sich die Theilung der Latte für dieselbe
durch die 1000' Latte bestimmte Fädendistanz wie folgt:
Distanzen.
Werthevon x bei der
500'Latte.
Werthevon x bei der
1000'Latte.
50'
0,7325'
–
100
1,4970
1,5147
150
2,2361
2,2752
200
3,0296
3,0376
300
4,5631
4,5679
400
6,0968
6,1000
500
7,6307
7,6328
600
–
9,1658
700
–
10,6992
800
–
12,2327
900
–
13,7663
1000
–
15,3000
Die Reductionstabellen folgen unter C, D, E und F und bedürfen nur der Bemerkung, daß die Werthe von δ hier gewöhnliche oder Sexagesimal-Grade
bedeuten.
A.
Textabbildung Bd. 116, S. 44
Reduction für die Elevation
A.
Textabbildung Bd. 116, S. 45
Reduction für die Elevation
B.
Textabbildung Bd. 116, S. 46
Reduction für die Depression.
B.
Textabbildung Bd. 116, S. 47
Reduction für die Depression.
Textabbildung Bd. 116, S. 48
Textabbildung Bd. 116, S. 49
Textabbildung Bd. 116, S. 50
Textabbildung Bd. 116, S. 51
Tafeln