| Titel: | Ueber das neue Planimeter des Kaspar Wetli, Ingenieur im Kanton Zürich; von Prof. Simon Stampfer. |
| Fundstelle: | Band 116, Jahrgang 1850, Nr. LXXXV., S. 424 |
| Download: | XML |
LXXXV.
Ueber das neue Planimeter des Kaspar Wetli, Ingenieur im
Kanton Zürich; von Prof. Simon
Stampfer.
Aus den Sitzungsberichten der mathem. naturw. Classe der kaiserl.
Akademie der Wissenschaften, durch die Zeitschrift des österr.
Ingenieur-Vereins 1850, Nr. 7.
Mit Abbildungen auf Tab.
VI.
Stampfer, über Wetli's neues Planimeter.
1. Die Aufgabe, aus geometrischen Karten oder Plänen den Flächeninhalt der
verschiedenen größeren und kleineren Figuren zu berechnen, kömmt den praktischen
Geometern unzähligemal vor; ja in der Regel werden geometrische Aufnahmen nur zu dem
Zweck gemacht, um den Flächeninhalt der verschiedenen Grundstücke mittelst der
erhaltenen Zeichnung kennen zu lernen. Man denke nur an den Kataster, wo die Fläche
eines jeden Grundstückes erhoben werden muß, mithin die Aufgabe nicht nur viele
tausendmal, sondern selbst millionenmal sich wiederholt. Es hat daher seit langer
Zeit nicht an Bemühungen gefehlt, diese Berechnungen durch mechanische Hülfsmittel
zu erleichtern und zu beschleunigen. Die zahlreichen Apparate dieser Art lassen sich
in zwei Classen theilen: 1) solche, welche nur die Abmessung von Grundlinie und Höhe
oder der Coordinaten erleichtern, indem sie die Anwendung des Cirkels beseitigen;
die Fläche selbst ergibt sich erst durch wirkliche Multiplication der Factoren oder
mittelst Multiplicationstafeln, dergleichen beim österreichischen Kataster wirklich
im Gebrauche sind.
Zur zweiten Classe gehören jene Apparate, welche auch die Multiplication ersparen und
die Fläche unmittelbar angeben sollen. Die große bisher nicht überwundene
Schwierigkeit besteht darin, das Product zweier variablen Factoren durch eine
einfache Operation mittelst einer Scale auszudrücken. Die
Erfinder der bisher bekannt gewordenen Vorschläge dieser Art leisten dieses auch
nicht unmittelbar, sondern sie reduciren sich mittelst ihres Apparates die Figur,
welche auf das Dreieck oder Trapez beschränkt ist, auf eine andere, deren eine
Factor eine constante Größe hat, wodurch die Fläche der Figur dem zweiten Factor proportional
wird. Hieher gehört das Wagner'sche Planimeter, zu den
vorzüglichsten dieser Art aber das neue patentirte Planimeter von Horsky und Kraft, welches die
Fläche durch zwei einfache Operationen wenigstens so sicher gibt, als die
gewöhnliche Berechnung mit Enkel und Maaßstab. Allein der Apparat ist nicht nur auf
die Elementarfiguren Dreieck und Viereck beschränkt, sondern die Anwendung
modificirt sich auch auf mehrere Arten, je nach der Größe der Figur oder nach dem
Verhältnisse der beiden Factoren. Die Planimeter der zweiten Art haben bis jetzt bei
den praktischen Geometern wenig Eingang gefunden; ihr Wirkungskreis ist zu
beschränkt, und es kommen zu viele Fälle vor, wo die Anwendung umständlich und
mühsam wird.
Alle bisher bekannten derartigen Hülfsmittel läßt das neue Planimeter von Wetli weit hinter sich zurück. Dieser sinnreiche Apparat
gibt die Fläche jeder beliebigen gerad- oder krummlinigen Figur immer durch
dieselbe höchst einfache Operation, nämlich indem man mit einer Spitze, die wie bei
einem Pantographen nach allen Richtungen beweglich ist, die Umfangslinie der Figur
beschreibt. Manche können im ersten Augenblick fragen, wie dieß seyn könne, da die
Fläche keine Function der Umfangslinie ist und Figuren von gleicher Umfangslinie
sehr verschiedene Fläche haben können. Allein die Sache ist, wie wir sehen werden,
ganz richtig.
Beschreibung des
Instrumentes.
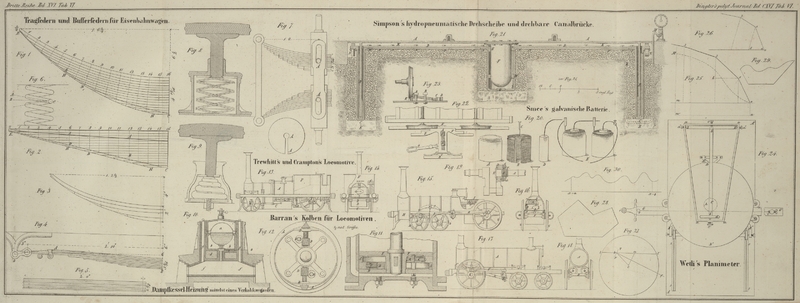
2. Figur 24
ist die horizontale Projection des Instrumentes in 1/3 der natürlichen Größe,
welches auf einer starken Metallplatte A, A' aufgebaut
ist. Ein dreifüßiges Gestell, ähnlich dem eines Theodoliten, läuft mittelst Rollen,
welche an den Enden der Füße bei B, B', B'' sichtbar
sind, auf parallelen Schienen s, s wie ein Wagen hin und
her. (Die mittlere Schiene und Rolle für den Fuß B ist
durch die Achse b, b' gedeckt.)
In der Mitte des Dreifußes erhebt sich eine senkrechte Achse, um welche die Scheibe
D, D' mit genau ebener Oberfläche nach Art eines
Theodolits sich dreht.
G, G' ist eine prismatische Stange, die sich zwischen
zwei Paar Rollen, welche mit dem Dreifuße in fester Verbindung stehen und in der
Zeichnung sichtbar sind, in einer zu den Schienen s, s
senkrechten Richtung bewegt.
Am Ende dieser Stange bei i befindet sich ein senkrechter
Stift, nach unten in eine Spitze auslaufend, welche, wie man sieht, auf einer unterlegten Zeichnung
nach allen Richtungen beliebig herumgeführt werden kann.
Längs der Stange G, G' ist ein Silberdraht e, e' ausgespannt, der sich um die unter der Scheibe an
ihrer Achse befindliche Welle h schlingt und beim
Hin- und Herschieben der Stange die Scheibe in Umlauf setzt.
Ferner ist E, E' ein auf der Platte A, A' senkrecht stehender Ständer, mit welchem der
Rahmen a, a, a, a mittelst der Schraubenspitzen a' wie ein Hebel verbunden ist. Dieser Rahmen trägt
durch die Schraubenspitzen c, c' die Achse b, b', an deren vorderem Ende sich die Rolle d befindet. Der ganze Rahmen sammt der Achse b, b' liegt mittelst der Rolle d auf der Scheibe auf, wobei die Anordnung so getroffen ist, daß die Achse
b, b' durch die Verlängerung der Achse C geht, und sowohl zu den Schienen s, s als auch zur Ebene der Scheibe parallel ist.
Die Rolle d rutscht nun, wie man leicht sieht, bei der
Bewegung des Wagens auf der Scheibe in einem Durchmesser derselben hin und her; eine
Verschiebung der Stange hingegen in der Richtung ihrer Länge dreht die Scheibe,
welche zugleich die Rolle d durch Friction in Umlauf
setzt. Die Scheibe besteht aus Messingblech, oder noch zweckmäßiger aus einer plan
geschliffenen Glastafel, und ist zur Vermehrung der Reibung mit feinem
gleichförmigem Papier überzogen.
Um die Achsendrehung der Rolle d zu messen, ist am
Ständer E, E' ein eingetheilter Kreis, und an der Achse
b, b' ein Zeiger befestigt; oder es befindet sich
umgekehrt der Kreis an der Achse und der Zeiger am Ständer. Welche Einrichtung
zweckmäßiger sey, wird weiter unten sich ergeben. Endlich befindet sich noch am
Ständer ein Rädchen, welches in ein bei b an der Achse
befindliches Getriebe eingreift und dazu bestimmt ist, die Umläufe der Rolle d zu zählen, während der vorhin erwähnte Kreis die
Theile eines Umlaufes angibt. Diese letzteren Bestandtheile sind in der Zeichnung
weggelassen, damit dieselbe nicht zu überladen erscheine.
Alle Schrauben, deren Spitzen als Umdrehungsachsen dienen, sind mit Gegenmuttern
versehen, überhaupt alle Theile mit großer Sorgfalt bearbeitet, um nicht nur
möglichst richtige, sondern auch möglichst leichte Bewegungen zu erzielen. Durch
eine besondere Vorrichtung läßt sich mittelst einer Schraube die Berührung der Rolle
d mit der Scheibe aufheben; der Wagen kann an dem
einen Endpunkte seiner Laufbahn arretirt werden u.s.w.
Der Erfinder überschickte einen solchen Apparat an den Werkmeister am hiesigen
polytechnischen Institut, Hrn. C.
Starke, und dieser hat in Gesellschaft mit ersterem sich ein ausschließliches
Privilegium auf die Verfertigung solcher Planimeter im Inlande erworben. Das
vorliegende Exemplar ist, außer einigen Abänderungen, die nach zahlreichen Versuchen
zweckmäßig erschienen, dem ursprünglichen Muster nachgebildet.Der Preis, um den solche Planimeter werden geliefert werden können, ist noch
nicht genau ermittelt, wird sich aber auf 150–180 fl. Conv.-M.
belaufen.
Theorie des Instrumentes.
3. Die gegenseitige Bewegung der Scheibe und der Rolle d
läßt sich als jene zweier Winkelräder ansehen, wobei der Halbmesser des einen Rades
stets veränderlich ist.
Sey der Halbmesser der Welle h + Halbmesser des Drahtes =
r, Halbmesser der Rolle = R; Abstand des Berührungspunktes der Rolle vom Centrum der Scheibe = ϱ, positiv bei der in der Figur angedeuteten
Lage. Die zu messende Figur werde auf Coordinaten bezogen, welche zu den beiden
Grundbewegungen des Apparates parallel sind, und zwar sollen die x zur Stange G, G', die y zu den Schienen s, s
parallel seyn, und der Anfangspunkt der x und y mit jenem der Bewegung zusammenfallen. Nur die
Bewegung nach x bringt eine Drehung der Scheibe hervor;
ist dieser Drehungswinkel = φ, jener der Rolle =
v (φ und v in Bogenmaaß vorausgesetzt), so ist
x = rφ
und Rv = ϱφ.
Die letztere Gleichung gilt jedoch nur, wenn ϱ
constant ist, allein ϱ ist veränderlich, daher
haben wir die Relation
Rdv = ϱdφ.
Der allgemeine Werth von ϱ ist = ϱ₀ + y wo ϱ₀ der Werth von ϱ für den Anfangspunkt o; ferner ist
aus der ersten Gleichung dφ = dx/r mithin Rdv = (ϱ₀ +
y) dx/r, woraus
Rrv = ϱ₀x + ∫ydx . . . . . . (1)
Die rechte Seite dieser Gleichung drückt offenbar eine Fläche aus, die demnach, da
Rr constant ist, der Winkelbewegung v proportional ist. Ist oM (Fig.
25) eine beliebige Curve, deren Gleichung y =
f(x), so ist für om = x, die Fläche oMm = ∫ydx. Macht man ao
= ϱ₀ und zieht am' parallel
zu om, so ist die Fläche aoMm' = ϱ
₀x
+ ∫ydx = Rrv, mithin die Bedeutung dieser Gleichung vollständig klar. Der Apparat
kann daher als eine Integrationsmaschine für das Differential f(x
)dx
angesehen werden, wenn die Curve y = f(x) in einer
Zeichnung gegeben ist.
Wir wollen nun (Fig.
25) als zu berechnende Figur ein geradliniges Polygon von n Seiten annehmen; seine Endpunkte seyen der Ordnung
nach mit 0, 1, 2, 3 ... (n – 1) bezeichnet; ϱ₀, ϱ₁, ϱ₂, etc. seyen die
Werthe von ϱ, wenn sich der beschreibende Punkt
i in 0, 1, 2 etc. befindet. Ist der Winkel der
ersten Seite mit der Abscissenachse = α₁,
so ist
y = x tang
α₁,
mithin nach (1), wenn das Integral von x = o bis x = x₁ genommen wird
Rrv₁ = ϱ
₀
x₁ + 1/2 x₁² tang α₁
= x₁ (ϱ₀ + 1/2 y₁).
Denkt man sich jetzt den Punkt 1 als Ursprung, b1 parallel zu am gezogen, und setzt b1 = x', b2 = y', so wird für
die Bewegung von 1 bis 2 ganz wie vorhin
Rrv₂ = x' (ϱ₁ + 1/2
y')
aber x' = x₂ – x₁; y' = y₂ – y₁,
mithin
Rrv₂ = (x₂ – x₁) [ϱ₁ + 1/2 (y₂ – y₁)]
eben so
Rrv₃ = (x₃ – x₂) [ϱ₂ + 1/2 (y₃ – y₂)] u.s.w.
Die letzte Seite, mit welcher die Spitze auf den Anfangspunkt zurückkehrt, gibt
Rrvn = (xn – xn – ₁) [ϱ
n – ₁ + 1/2 (yn – yn –
₁)].
Nun ist
ϱ₁ = ϱ₀ + y₁
ϱ₂ = ϱ₀ + y₂
überhaupt
ϱm = ϱ₀ + y
m
daher erhalten wir
RrΣv
= x₁ (ϱ₀ + 1/2 y₁)
+
+ (x₂
– x₁) [ϱ₀ + 1/2 (y₁ +
y₂)]
+ (x₃
– x₂) [ϱ₀ + 1/2 (y₂ +
y₃)]
.
.
.
+ (xn –
xn –
₁) [ϱ₀ + 1/2 (yn –
₁ + yn)]
xn, yn sind die Coordinaten
für den Anfangspunkt, mithin = 0; ferner ist der in ϱ₀ multiplicirte Theil
= ϱ₀ [x₁ + (x₂
– x₁) + (x₃ – x₂) + ... + (xn – xn –
₁)],
wo der eingeklammerte Factor, mithin der ganze Ausdruck
verschwindet. Es bleibt demnach, wenn wir jetzt Σv = V setzen und die ganze Gleichung
mit 2 multipliciren,
2 RrV = 2 F = x₁y₁ + (x₂
– x₁) (y₁ + y₂) +
+ (x₃ – x₂) (y₂ + y₃) + ... + (xn – xn – ₁) (yn – ₁ + yn)
ein bekannter Ausdruck für die doppelte Fläche eines Polygons,
der sich auch in den folgenden transformiren läßt:
2 F = y₁ (x₂ – x₀) + y₂ (x₃ – x₁) + y₃ (x₄ – x₂) + ...
+ yn – ₁ (x
n – xn – ₂),
wo x₀ und x
n = 0 und nur der Symmetrie wegen angesetzt
sind.
Da ϱ₀ aus dem Ausdrucke für die Fläche
verschwunden ist, so ist diese von der anfänglichen Lage der Rolle d gegen den Mittelpunkt C
unabhängig, und man kann diese Lage, die Stellung der Figur gegen den Apparat, sowie
den Anfangspunkt irgendwo am Umfange derselben beliebig wählen.
Der gegebene Beweis erstreckt sich auch auf alle wie immer gestalteten krummlinigen
Figuren, da jede solche als ein geradliniges Polygon von unendlicher Seitenzahl
angesehen werden kann.
Die Größe RrV, welche die Fläche der Figur angibt,
kann man sich als einen Kreissector denken, dessen Winkel, im Bogenmaaß ausgedrückt,
= V und dessen Halbmesser R'
= √(2Rr). Man
kann dieses R' den äquivalenten Halbmesser nennen.
4. Die Anordnung wird so getroffen, daß V nicht Gradmaaß,
sondern unmittelbar Flächenmaß gibt. Am vorliegenden Instrumente ist ein Umlauf, d.h. 2 Rr
π = 2 Wiener Quadratzoll gesetzt, wo dann
Rr = 1/π = 0,₃₁₈₃₁
wird. Nimmt man noch das Verhältniß der Halbmesser zweckmäßig
an, so ergeben sich diese einzeln. Die halbe Peripherie oder der Quadratzoll ist in
100 Theile getheilt und die Tausendtheile lassen sich leicht nach dem Augenmaaße
schätzen. Beim österreichischen Kataster ist bekanntlich der Quadratzoll = 1
österreichisches Joch, daher der Apparat in diesem Falle die Fläche unmittelbar in
Jochen und deren Decimalen angibt. Das oben erwähnte Rädchen zählt die ganzen
Quadratzolle. Der Spielraum der beiden Grundbewegungen beträgt bei gegenwärtigem
Apparate in der Richtung der Schienen 6, in der Richtung der Stange 8 Zoll, mithin
kann die größte noch unmittelbar meßbare Fläche bis 48 Quadratzoll steigen, ein
Umfang, der für die Praxis vollkommen genügen dürfte.
Genauigkeit des
Instrumentes.
5. Was die Schärfe betrifft, mit welcher der Apparat den Flächeninhalt angibt, so
hängt dieselbe von der Vollkommenheit der Ausführung von Seite des Mechanikers
sowohl, als auch, wie sich von selbst versteht, von der Genauigkeit ab, mit welcher
die Spitze auf der Umfangslinie der zu messenden Figur herumgeführt wird. Mein
erstes Bedenken war, ob denn wohl die bloße Reibung im Stande sey, die Rolle d genau der Bewegung der Scheibe gemäß ohne alles
Schleifen umzudrehen. Vielfältige Versuche zeigten jedoch, daß dieses wirklich im
hohen Grade der Fall sey, wenn die Bewegung nicht zu rasch ist und jeder plötzliche
Stoß vermieden wird. Ausführlicheres hierüber in §. 13 und 14. Ist der
Apparat in seinen Bewegungen gehörig fehlerfrei, so ist seine Genauigkeit so groß,
daß diese durch die gewöhnlichen Methoden, die Fläche einer gezeichneten Figur zu
berechnen, gar nicht controllirt werden kann, weil dieselben größeren Fehlern
unterworfen sind. Diese Schärfe bezieht sich begreiflich nur auf jene Figur, deren
Umfangslinie die Spitze i wirklich beschreibt. Um nun
dieselbe nachweisen zu können, ist eine Messingplatte beigegeben, auf welcher Kreise
und Rechtecke durch starke und tiefe Linien eingeschnitten sind, in denen die Spitze
mit großer Sicherheit herumgeführt werden kann. Diese Figuren wurden zugleich unter
den Mikroskopen des Comparators abgemessen, wodurch sich ihr wahrer Flächeninhalt ergibt, der für die
Angaben des Apparates als Controlle dient.
Wir lassen einige Abmessungen dieser Originalfiguren folgen, wobei bemerkt wird, daß
aus mehreren Versuchsreihen solche ausgewählt sind, die nicht zu den
bestharmonirenden gehören. Die erste Columne enthält die Angaben des Instrumentes
nach 1, 2, 3 etc. maliger Umschreibung der Figur, wobei die ganzen Quadratzolle nur
bei den zwei ersten Ablesungen angesetzt wurden, da selbe für die Fortsetzung
unnöthig sind. Die Differenz zweier auf einander folgender Ablesungen gibt die
Fläche der Figur.
Kreis Nr.
1.
Kreis Nr.
2.
Angabendes Instrumentes.
Flächein Quadratzoll.
Angabendes Instrumentes.
Flächein Quadratzoll.
6,050
......
23,269
......
13,114
7,064
28,176
4,907
182
068
084
908
246
064
993
909
312
066
903
910
383
071
809
906
450
067
719
910
516
066
624
905
582
066
535
911
652
070
441
906
720
068
350
909
Mittel . . .
F = 7,0670
Mittel . . .
F = 4,9081
Man kann auch das Endresultat aus den zweifachen, dreifachen u.s.w. Flächen ableiten,
indem man jede Lesung von jener nach zwei, drei etc. Wiederholungen abzieht,
überhaupt ganz so verfahren, wie bei der Multiplication der Winkel. Man erhält z.B.
aus den doppelten Werthen für den Kreis Nr. 1 im Mittel F
= 7,0671. Der Apparat gibt gegenwärtig die Flächen sehr nahe um 1/1000 F zu klein; gibt man diese Verbesserung hinzu, so erhält
man
F₁ =
7,0750 F₂ = 4,9130.
Die wahren Werthe (bei 13° R.) sind:
F₁ =
7,0741 F₂ = 4,9125.
Aus vorstehenden Versuchen folgt der mittlere Fehler einer einzelnen Messung beim
Kreis Nr. 1 = 0,0018 Quadratzoll oder nahe 1/4000 des Ganzen. Man sieht demnach, daß
der Apparat eine Genauigkeit zu erreichen im Stande ist, die jene der praktischen
Anwendung auf gezeichnete Figuren weit übertrifft, da man nicht im Stande ist, die
Umfangslinie mit mathematischer Strenge zu beschreiben. Und selbst wenn dieses der
Fall wäre, wäre kaum etwas gewonnen, da keine durch wirkliche Aufnahme entstandene
verjüngte Figur auf dem Papiere das Original auf dem Felde vollkommen getreu
darstellt, sondern mit den unvermeidlichen Fehlern behaftet ist, welche bei der
Aufnahme und Construction begangen werden. Die vorhin angegebene Genauigkeit läßt
sich jedoch nur nach einiger Uebung und mit Anwendung großer Vorsicht erreichen,
Bedingungen, die bekanntlich bei allen Messungsversuchen vorhanden seyn müssen, wo
der höchste Grad von Schärfe angestrebt wird. Die Biegung des vorderen Theiles der
Stange und des Stiftes, die Einwirkung der Temperatur u.s.w. treten bei diesen
feinen Versuchen störend auf, obschon diese Fehlerquellen für die gewöhnliche
Anwendung unmerklich sind, wenn der Apparat im Uebrigen gehörig adjustirt ist. Der
gefundene mittlere Fehler = 0,0018 Quadratzoll beim Kreis Nr. 1 entspricht einer
Aenderung = 0,0002 Zoll seines Halbmessers, und der geringste Druck der Spitze nach
der inneren oder äußeren Seite vermag dieselbe um eine so kleine Größe gegen ihre
wahre Lage zu verrücken. Wir haben bei diesen Versuchen den Stift i mit einem kleinen Gewichte beschwert, die Linien auf
der Messingplatte eingeölt und von Staub oder Schmutz frei gehalten, endlich die
Stange mit der Hand so herum zu führen gesucht, daß die Spitze keinen Seitendruck
erleidet. Auch muß die Unterlage, Tisch oder Reisbrett gehörig eben seyn. Für die
gewöhnliche Anwendung fallen alle diese Feinheiten natürlich weg; ich habe unsere
Erfahrungen nur anführen wollen, falls Andere eine ähnliche Schärfe zu erreichen
wünschen.
Da es von besonderem Interesse ist, die Genauigkeit kennen zu lernen, welche der
Apparat bei der gewöhnlichen Anwendung auf gezeichnete Figuren gibt, so füge ich die
Abmessungen von zwei Figuren an, welche in Fig. 28 und 29 in 1/3
ihrer Größe ungefähr vorgestellt sind.
Figur 28.
Figur 29.
Angabendes Instrumentes.
Flächein Quadratzoll.
Angabendes Instrumentes.
Flächein Quadratzoll.
3,290
......
29,374
......
14,098
10,808
33,901
4,527
24,922
824
38,444
543
713
791
979
535
513
800
533
554
333
820
083
550
151
818
622
539
Mittel . . . .
10,810
4,541
Mittlerer Fehler einer einzelnen Messung
±
0,010
± 0,009
Diese Abmessungen waren die ersten Versuche, welche ein in geometrischen Arbeiten
sehr geübter Ingenieur mit dem Apparate ausführte, wobei er sich auf meinen Wunsch
eines ängstlichen Strebens nach Genauigkeit absichtlich enthielt, was auch schon aus
dem Umstande hervorgeht, daß er zu einer einzelnen Messung der Fig. 28 sammt Ablesen und
Aufschreiben durchschnittlich nur 1 2/5 Minuten Zeit brauchte. Praktiker werden von
selbst sehen, wie befriedigend die Uebereinstimmung dieser Versuche ist, und daß
eine solche bei den gewöhnlichen Berechnungsmethoden selbst mit Anwendung großer
Sorgfalt schwer erreichbar sey, da z.B. bei Fig. 28 der mittlere
Fehler einer Messung nur etwa 1/1100 des Ganzen beträgt.
6. Die Vortheile, welche dieser Apparat bei der Flächenberechnung geometrischer
Zeichnungen gewähren muß, sind demnach so augenfällig, daß es überflüssig ist,
dieselben weiter auseinander zu fetzen. Der große Zeitgewinn wird vorzüglich dort
hervortreten, wo derlei Berechnungen in großer Anzahl vorkommen, z.B. beim Kataster,
wo der Apparat auch zu Revisionen besonders geeignet ist, weil er größere Partien
als eine Figur zu behandeln gestattet. Ferner bei
Eisenbahnbauten zur Berechnung der zu expropriirenden Parzellenstücke und der
zahlreichen Querprofile u.s.w. Practiker werden auch den wesentlichen Umstand zu
würdigen wissen, daß hier Rechnungsfehler fast gänzlich ausgeschlossen sind, da bei
jeder beliebigen Figur nur die Angaben des Instrumentes anfangs und am Ende, also im Ganzen zwei
Zahlen aufzuschreiben sind.
Auf eine besondere Anwendung des Instrumentes, welche in den Wirkungskreis der
Naturwissenschaften gehört, erlaube ich mir noch aufmerksam zu machen. Man hat in
neuerer Zeit angefangen, mehrere physikalische, besonders meteorologische
Erscheinungen durch mechanische Vorrichtungen, sogenannte Autographen, aufzeichnen
zu lassen, z.B. den Barometerstand, die Temperatur, die Richtung und Stärke des
Windes u.s.w. Diese Apparate stellen die zu messende Größe, z.B. den Barometerstand,
bekanntlich graphisch durch eine krumme Linie dar, wobei die Ordinaten den
Barometerstand vorstellen, und die Abscissen der Zeit proportional sind. Fig. 30 stellt
eine solche Curve dar. Wenn es sich nun darum handelt, den mittleren Barometerstand,
d.h. den mittleren Werth von y für ein gegebenes
Zeitintervall von x = a bis
x = b zu finden, so ist
streng richtig dieser mittlere Werth
= (∫abydx)/(b –
a)
d.h. gleich der Fläche zwischen der ersten und letzten
Ordinate getheilt durch das dazwischenliegende Stück der Abscissenachse. Solche
mittlere Werthe lassen sich, wie man sieht; mit dem neuen Planimeter eben so leicht
als genau finden. Wenn auch gegenwärtig derlei autographische Apparate noch nicht
jene Genauigkeit geben, welche erforderlich ist, um aus den graphischen Curven die
mittleren Werthe mit gewünschter Schärfe erhalten zu können, so läßt sich doch
erwarten, daß die Zukunft auch hierin Fortschritte machen, und solche Autographen
immer mehr vervollkommt bei dergleichen Beobachtungen in Anwendung bringen
werde.
Bemerkungen über die Construction und
Adjustirung des Apparates; Untersuchung der verschiedenen Fehlerquellen
desselben.
7. Die Richtigkeit der Leistungen des Apparates hängt von der richtigen Construction
seiner Theile, von der genauen Ausführung derselben, und von der scharfen
Rectification der Bewegungen ab, damit diese der theoretischen Voraussetzung
entsprechen. Ich will nun in Bezug auf die wesentlichen und unwesentlichen
Eigenschaften des Apparates dasjenige mittheilen, was ich durch vielfache Versuche
und Untersuchungen gefunden habe.
a) Es ist nicht nöthig, daß die beiden Grundbewegungen
genau auf einander senkrecht stehen, sondern sie können auch einen anderen
constanten Winkel mit einander bilden. Ist dieser = β (Fig. 26) und werden die schiefwinkligen Coordinaten mit x', y' bezeichnet, so ist für die Bewegung von 0 bis 1
gemäß §. 3
y = (x' sin
α)/sin (α + β)',
welcher Werth in Formel (1) gesetzt gibt
Rrv₁ =
ϱ₀x'₁ + 1/2 x'₁² sin
α/sin (α + β) = x'₁ (ϱ₀ + 1/2 y'₁),
eben so
Rrv₂ = (x'₂ – x'₁) [ϱ₁ + 1/2 (y'₂ – y'₁)] u.s.w.,
mithin folgt wie früher:
2 RrV = y'₁ (x'₂ – x₀) + y'₂ (x'₃ – x'₁) + y'₃ (x'₄
– x'₂) + ...
also auch
2 RrV
sin β = sin β
[y'₁ (x'₂
– x'₀) + y'₂ (x'₃ – x'₁) + ....]
Allein der zweite Theil der letzteren Gleichung ist = 2 F, wenn F die Fläche des Polygons, mithin ist auch
hier
F = RrV sin β
der Winkelbewegung V
proportional.
b) Die Achse der Rolle sey zwar zur Ebene der Scheibe
parallel, sie kann aber mit der Bewegung des Wagens einen beliebigen Winkel bilden,
auch ist es nicht nothwendig, daß die Berührungslinie der Rolle mit der Scheibe
durch den Mittelpunkt C gehe.
Sey (Fig. 27)
pq die Rolle, bf ihre Achse, ll' die Berührungslinie,
welche die Rolle auf der Scheibe bei bloßer Bewegung des Wagens beschreibt, und die
mit der Richtung der y parallel seyn muß. Ist c
a senkrecht auf b
f gezogen, so ist a ein
unveränderlicher Punkt auf ll', von welchem wir
die Bewegung nach y zählen wollen. Sey ab
= g, cb = ϱ, der constante < abf = γ, der
veränderliche Winkel bcf = α, so ist
Rdv = ϱ cos αdφ, ferner im ∆ abc : ϱ sin c = g
sin a,
aber < c = 90 – α; < a =
90 – γ,
mithin
ϱ = g
cos γ/cos α, und Rdv = g cos γ d
φ.
Setzt man das unbestimmte g = g₀ + y, wo g₀ mit dem früheren ϱ₀
gleiche Bedeutung hat, so folgt, da dφ =
d
x/r, ganz nach der früheren
Ableitung
Rrv/cos
γ = g
₀x
+ ∫ydx
und für das Polygon
F = Rrv/cos γ.
Man sieht leicht, daß die constanten Winkel β oder
γ in den Ausdrücken Rr
sin β, Rr/cos γ nicht bekannt zu seyn brauchen, indem die
Halbmesser R, r so adjustirt werden, daß der Apparat die
Flächen richtig gibt.
c) Endlich ist es nicht erforderlich, daß die Achse der
Rolle zur Ebene der Scheibe parallel sey, denn die gegenseitige Achsendrehung hängt
nur von den Halbmessern, nicht aber von einer constanten Neigung der Rolle gegen die
Scheibe ab.
Es ist demnach unnöthig, Correctionsschrauben anzubringen, um die Achse der Rolle
sowohl zur Ebene der Scheibe, als zu den Schienen s, s
genau parallel zu stellen, die Berührungslinie durch den Mittelpunkt C zu führen, oder die beiden Grundbewegungen auf
einander genau senkrecht zu bringen, sondern es genügt, wenn diese Eigenschaften
näherungsweise vorhanden sind.
8. Die Rolle von Stahl ist am Rande cylinderförmig abgerundet, und die an demselben
herumlaufende Berührungslinie soll genau in einer zur Umdrehungsachse senkrechten
Ebene liegen. Damit dieß der Fall sey, muß nicht nur die Rolle selbst richtig
bearbeitet, sondern auch die Scheibe senkrecht zu ihrer Achse, ihre Ebene zur
Bewegung des Wagens parallel und möglichst frei von Unebenheiten des Papiers seyn.
Um jedoch den Einfluß solcher Unebenheiten, die in aller Strenge nie vermieden
werden können, mehr unschädlich zu machen, soll der Halbmesser der Krümmung am Rande
der Rolle 1/4 bis 1/3 Linie nicht übersteigen. Durch häufigen Gebrauch wird der Rand
der Rolle, obschon gehärtet, sich wahrscheinlich etwas abschleifen, wodurch ihr
Halbmesser sich verkleinert und die Angaben des Instrumentes zu groß werden. Man kann diesem Fehler,
sobald er seiner Größe halber nicht mehr vernachlässigt werden kann, durch einen
etwas dickern Draht abhelfen, oder denselben mittelst einer Correctionstabelle
verbessern.
9. Die Bewegung des Wagens drückt die Achse b, b' gegen
die Spitze c oder c';
gleichzeitig entsteht ein ähnlicher Druck auf die Achse C nach der einen oder anderen Seite. Soll hiedurch kein Fehler entstehen,
so dürfen die Achsen keinen Spielraum in ihren Lagern haben. Dasselbe gilt von den
Rollen des Wagens und der Stange. In jedem dieser Fälle kann der schädliche Einfluß
als hinreichend weggeschafft angesehen werden, wenn durch das Gefühl mittelst der
Hand kein Spielraum mehr bemerkt wird. Man kann dabei auf folgende Weise verfahren.
Man öffne z.B. bei der Achse b, b' die Schraube c', bis man den Spielraum deutlich fühlt, schließe sie
wieder allmählich, bis kaum eine Spur des Spielraumes mehr bemerkbar ist, und gebe
noch eine ganz kleine Bewegung der Schraube hinzu. Indessen ist, besonders bei den
Achsen der Rolle und Scheibe, selbst ein sehr kleiner Spielraum der Erfahrung gemäß
ohne bedeutenden Einfluß, während ein zu starkes Klemmen dieser beiden Achsen
sogleich Störungen in der Nichtigkeit des Instrumentes erzeugen kann. Die
Rollenachsen am Wagen können auf folgende Art regulirt werden. Man hält den Wagen
so, daß die Rolle ganz frei ist, setzt sie mit dem Finger in Umlauf, und klemmt so
weit, bis die Leichtigkeit der Bewegung eben anfängt gehemmt zu werden. Bei der
Stange hat man nur den Spielraum in horizontaler Richtung zu beachten, an
verschiedenen Stellen der Länge nach zu prüfen und durch die angebrachten
Correctionsschrauben zu reguliren. Bei der Achse C
geschieht dieses durch die Schraubenspitze an ihrem unteren Ende. Die Spitzen a' können ohne Nachtheil etwas stärker geklemmt
seyn.
10. Die Spitze i soll eine gerade Linie beschreiben, wenn
die Stange bei feststehendem Wagen hin und her geführt wird. Deßhalb muß nicht nur
die Stange gerade seyn und während der Bewegung sich selbst parallel bleiben,
sondern es darf auch keine Drehung um ihre Länge vor sich gehen, wodurch die tiefer
liegende Spitze verrückt werden würde; oder mit anderen Worten, auch der senkrechte
Stift muß sich selbst parallel bleiben. Die Schienen, auf welchen der Wagen läuft,
müssen ebenfalls gehörig gerade und unter sich parallel seyn; am wichtigsten ist
dieß bei der mittleren Schiene, weil sonst während der Bewegung zugleich eine
Drehung des Wagens und der damit verbundenen Stange entsteht. Eine sichere Prüfung
in dieser Beziehung erhält man, wenn man ein kleines mit einem Fadenkreuze
versehenes Fernrohr mit dem Wagen parallel zu den Schienen verbindet und beobachtet, ob die Visur während
der Bewegung des Wagens an einem entfernten Objecte unverändert bleibt. Wenn die
Bewegung der Visur in der Entfernung = D die Größe D/2000 nicht übersteigt, während der Wagen seine ganze
Bahn zurücklegt, kann der Fehler als ganz unmerklich angesehen werden.
Der Draht ist immer auf jener Seite mehr gespannt, nach welcher die Stange sich
bewegt, wodurch beim Wechsel der Bewegung ein kleiner todter Gang in der Umdrehung
der Scheibe entsteht. Indessen ist dieser nach meiner Erfahrung unmerklich, wo es
nicht auf die höchste Schärfe ankommt, wenn der Draht gehörig gespannt und nicht zu
dünn ist, außer es wäre die Achse C zu stark geklemmt.
Die Dicke des Drahtes soll nicht wohl unter 1/100 Zoll betragen.
11. Folgende Versuche sind besonders geeignet, die Genauigkeit des Apparates zu
prüfen und seine Fehler zu entdecken.
1) Der Versuch mit den Kreisen auf der Messingplatte, worüber schon oben §. 5
Beispiele gegeben worden sind. Um den Fehler zu vermeiden, welcher dadurch entsteht,
daß am Ende der Bewegung die Spitze nicht ganz genau auf den Anfangspunkt zu stehen
kömmt, wird dieser in jenem Durchmesser gewählt, welcher zur Bewegung der Stange
parallel ist.
2) Indem man den Stift am Rande eines Lineals fortführt, welches mit den beiden
Grundbewegungen einen schiefen Winkel bildet und gehörig befestigt ist. Bei
beliebiger Länge dieser Bewegung soll, wenn die Spitze genau auf den Anfangspunkt
zurückgeführt wird, die Ablesung am Kreise mit jener am Anfange gleich seyn, weil
die Fläche einer Linie = 0 ist. Um hier den Anfangspunkt scharf zu treffen, kann man
entweder den Stift oder die Stange mit einem festen Punkte behutsam zur Berührung
bringen, oder die Lage so wählen, daß für den Anfang die Rolle über dem Centrum der
Scheibe steht, in welchem Fall eine Marke am Lineale hinreicht.
3) Der vorige Versuch, jedoch das Lineal zur Stange parallel. Für den Anfang kann man
ebenfalls die Berührung mit einem festen Punkte wählen, oder die Stange so weit
zurückschieben, bis der an ihrer unteren Seite befindliche Stift den Dreifuß
berührt.
12. Der Stift soll sich in seiner Hülse, jedoch ohne geringsten Spielraum, so leicht
bewegen, daß er durch sein eigenes Gewicht sinkt. Durch eine angebrachte Feder
läßt er sich schwebend erhalten und überhaupt mehr oder weniger in der Hülse
feststellen; auch sind kleine Gewichte beigegeben, welche oben auf den Stift
aufgesetzt werden können, um sein Gewicht zu vermehren. Für Zeichnungen wird der
messingene Stift angewendet, dessen etwas abgestumpfte Spitze leicht auf dem Papiere
fortgleitet; der Stahlstift hingegen wird nur zu den Versuchen auf der beigegebenen
Messingplatte benützt.
Denkt man sich in der Achse des Stiftes und in gleicher Höhe mit der Mitte der Stange
einen festen Punkt, wir wollen ihn den correspondirenden Punkt nennen, so sieht man
leicht, daß der Apparat eigentlich die Bewegung dieses Punktes angibt, mithin Fehler
entstehen müssen, wenn während der Meßoperation die senkrechte Lage des Stiftes
Störungen erleidet. Ich mache auf diesen Fehler besonders aufmerksam, weil er schwer
oder gar nicht vermieden werden kann. Er entsteht auf mehrfache Art: 1) wenn die
Spitze am Rande eines Lineals fortgeführt und zugleich an denselben angedrückt wird,
wobei die beiden Kräfte, der Druck der Hand und der Gegendruck an der tiefer
liegenden Spitze, den Stift aus seiner verticalen Lage zu drehen suchen; 2) die
Stange sowohl als die übrigen Theile des Instrumentes geben dem Drucke etwas nach,
welcher nöthig ist, den Wagen und die Stange in Bewegung zu setzen; und endlich 3)
strebt die Reibung am Lineale die Spitze zurück zu halten. Durch geeignete Versuche
ist es mir gelungen, jede dieser drei Fehlerquellen nachzuweisen. Die zwei letzteren
sind bei zweckmäßiger Behandlung des Apparates, wenn dieser sonst in Ordnung ist,
für die gewöhnliche Anwendung verschwindend, die erstere hingegen kann bei stärkerem
Drucke ziemlich merklich werden. Der Fehler wird noch vergrößert, wenn die Hand
durch schiefen Druck die Stange zugleich zu drehen strebt, oder den Druck am obern
Theile der Stifthülse ausübt. Auch ist es nicht rathsam, den Stift mit dem Finger
niederzudrücken, weil dabei leicht ein Seitendruck eintreten kann.
Dieser Fehler läßt sich leicht nachweisen. Wenn man bei dem oben angeführten Versuche
Nr. 1 einen schwachen Druck nach außen anwendet, erhält man eine zu große Fläche,
weil hier der correspondirende Punkt einen größeren Kreis beschreibt als die Spitze.
Das Gegentheil ergibt sich bei einem Drucke gegen den Mittelpunkt.
Ordnet man den Versuch Nr. 3 so an, daß die Rolle nahe am Rande der Scheibe sich
befindet, und wendet bei der Bewegung rückwärts einen andern Druck an als jenen nach
vorwärts, so wird der Fehler hervortreten, sowohl im Verhältniß des
Druckunterschiedes als der Länge des Weges, wie die Theorie es verlangt, indem der correspondirende Punkt
hier nicht eine Linie, sondern eine sehr schmale Fläche umschreibt. Dieser Fehler
muß unter übrigens gleichen Umständen um so geringer seyn, je kleiner der Abstand
der Spitze von der Stange und je steifer diese ist, daher bei der Construction des
Instrumentes darauf gesehen werden muß, diesen Bedingen möglichst nachzukommen.
13. Wir haben noch eine der wesentlichsten Fehlerquellen näher zu betrachten, nämlich
jene, welche von der Bewegung der Rolle auf der Scheibe abhängt. Die Theorie
verlangt, daß der abgewickelte Bogen der Rolle genau die Länge der Curve habe,
welche der Berührungspunkt auf der Scheibe beschreibt. Diese Curve wollen wir die
Berührungscurve nennen. Demgemäß ergeben sich folgende zwei Forderungen: 1) der
Berührungspunkt der Rolle mit der Scheibe soll sich möglichst einem mathematischen
Punkte nähern, mithin die Oberfläche der Scheibe eine ganz glatte Ebene seyn; 2) die
Abwicklung der Rolle soll ohne gleitende Bewegung vor sich gehen.
Wie man sieht, ist es unmöglich, diese beiden Bedingungen genau zu erfüllen, sondern
es kann dieses bei der erstern nur annäherungsweise geschehen, weil es unerläßlich
ist, die Scheibe mit Papier zu überziehen, um die nöthige Reibung zur Umdrehung der
Rolle zu erhalten. Auf einer solchen rauhen Oberfläche werden die auf einander
folgenden Berührungspunkte beständig über der wahren Berührungscurve, wenn auch sehr
wenig, hin und her schwanken, und es wird somit eine gestörte Berührungscurve
entstehen. Diese Schwankungen werden um so größer seyn, je unebener das Papier und
je größer der Halbmesser der Abrundung am Rande der Rolle ist; man kann denselben
auch nicht zu klein machen, weil dadurch das Fortgleiten der Rolle zu sehr erschwert
und ihr Rand schneller abgenützt werden würde. Diese Abnützung verkleinert nicht nur
den Halbmesser der Rolle, sondern zerstört auch die regelmäßige Rundung ihres Randes
und wird deßhalb nach längerem Gebrauche die Genauigkeit des Apparates etwas
verringern. Indessen fehlen hierüber noch die Erfahrungen. Je dünner, fester und
gleichförmiger der Papierüberzug ist, desto besser; auf dickerem oder lockerem
Papier macht die Rolle einen merklichen Eindruck und der Berührungspunkt geht in
eine Fläche über, was nach unsern Erfahrungen sogleich sehr merkliche Störungen im
Gesetze der Bewegung zur Folge hat. Die Fehler, welche durch solche Störungen der
Berührungscurve entstehen, sind leicht zu unterscheiden, weil sie die einzigen sind,
die gar kein erkennbares Gesetz befolgen. Zu diesem Zweck wiederhole man den Versuch Nr. 1
vielmal hintereinander mit einerlei Art des Druckes, mit gleicher Geschwindigkeit,
überhaupt unter möglichst gleichen Umständen, wobei man den Apparat von Zeit zu Zeit
etwas verrückt, um die Berührungscurve auf andere Stellen des Papiers zu bringen.
Auch der Versuch Nr. 2 kann auf ähnliche Weise benützt werden. Befestigt man dabei
das Lineal in gleicher Höhe mit der Stange, um das Stangenende selbst am Lineale hin
und her führen zu können, so werden dadurch die vorhin besprochenen, durch das
Schwanken der Spitze entstehenden Fehler vermieden. Werden diese Versuche unter
möglichst gleichen Umständen mehrmals wiederholt, und es zeigen sich dabei
gesetzlose Unregelmäßigkeiten oder Sprünge, so ist die Ursache sicher in der
Papierfläche zu suchen, welche dann vor Allem weggeschafft werden muß, weil sich
sonst die übrigen Fehlerquellen nicht trennen und einzeln entdecken lassen. Solche
Untersuchungen und Erfahrungen führten uns darauf, den Papierüberzug so
herzustellen, daß Fehler dieser Art, wenigstens bei einem neuen Instrumente,
unmerklich sind.
Die Umdrehung der Rolle soll ohne gleitende Bewegung vor sich gehen. Bewegt sich die
Rolle, während sie um ihre Achse rotirt, zugleich gegen den Mittelpunkt der Scheibe
hin, so soll ihre Umdrehungsgeschwindigkeit genau wie der Halbmesser ϱ abnehmen. Allein wegen der Schwungkraft der
Rolle und der übrigen mit ihr sich drehenden Theile wird sie ein beständiges
Bestreben zum Vorlaufen äußern. Der umgekehrte Fall tritt ein, wenn die Rolle sich
vom Mittelpunkte der Scheibe entfernt. Soll in dieser Beziehung kein Fehler
entstehen, so muß die Reibung auf dem Papier im Stande seyn, die Wirkung der
Schwungkraft gehörig zu beherrschen. Diese Wirkung nimmt zu einerseits wie das
Quadrat der Geschwindigkeit, andererseits wie das Bewegungsmoment der rotirenden
Masse, und ließe sich einer Rechnung unterwerfen; allein wir beschränken uns darauf
praktisch auszumitteln, unter welchen Bedingungen an unserem Apparate der aus dieser
Quelle entspringende Fehler unmerklich ist. Zu dieser Untersuchung ist besonders der
Versuch Nr. 2 geeignet. Ein messingenes Lineal wurde in gleicher Höhe mit der Stange
so befestigt, daß es mit den Coordinaten-Achsen ungefähr einen Winkel von
45° bildete, und die Bewegung von ϱ = 0
bis ϱ = 2,5 Zoll ausgedehnt, was für den Stift
einen Weg von 3,5 Zoll gibt. Es wurden zwei Reihen von Versuchen unter Anwendung
verschiedener Geschwindigkeiten vorgenommen. Bei der ersten war an der Achse der
Rolle ein leichter Kreis von Messing befestigt, dessen Durchmesser = 3 1/2 Zoll und
Gewicht = 0,80 Loth, wovon 0,53 Loth auf den äußern Kranz fallen. Bei der zweiten
Versuchsreihe wurde der Kreis durch eine Scheibe aus Zeichenpapier von gleichem
Durchmesser ersetzt, im Gewichte = 1/20 Loth. Ich lasse die Mittelwerthe der
Resultate dieser Versuche hier folgen. Die erste Columne enthält die Zeitdauer der
einfachen Bewegung des Stiftes durch 3,5 Zoll. Die beobachteten Differenzen zwischen
der ersten und zweiten Ablesung wurden um 0,002 verkleinert, weil dieser Betrag
selbst bei sehr langsamer Bewegung vorhanden war, mithin nicht von der
Geschwindigkeit, sondern von einer andern Ursache abhängt.
Zeitdauer.
Kreis von
Messing.
Papierscheibe.
6 Sec.
0,0022 Quadratzoll
0,0005 Quadratzoll
3 „
0,0100
„
0,0018
„
2 „
0,0220
„
0,0038
„
Wie man sieht, verhalten sich diese Differenzen oder Fehler so nahe wie die Quadrate
der Geschwindigkeiten, als mit Rücksicht auf die Unsicherheit solcher Versuche nur
erwartet werden kann. Es ist somit entschieden, daß diese Fehler durch das Gleiten
oder Rutschen der Rolle entstehen, und wir ziehen daraus folgende Regel:
An der Achse der Rolle darf nur ein leichter Zeiger, nicht aber der eingetheilte
Kreis befestigt seyn, und überhaupt soll an der Rolle und ihrer Achse jede unnöthige
Masse vermieden werden. Unter dieser Bedingung wird die Bewegung der Rolle von der
Reibung so vollständig beherrscht, daß, übertrieben rasche oder stoßweise Bewegungen
ausgenommen, von dieser Seite kein merklicher Fehler zu befürchten ist.
15. Die Grundsätze und Regeln, welche bei der Anwendung des Apparates auf
geometrische Zeichnungen beobachtet werden sollen, ergeben sich großentheils aus der
bisherigen Darstellung, daher ich hierüber nur noch einige Andeutungen beizufügen
mir erlaube.
Aus der Gleichung Rrdv = ϱdx geht hervor, daß ein Fehler in x oder in der Richtung der Stange um so größeren Einfluß
habe, je größer ϱ ist. Bei unsern Instrumenten
kann ϱ drei Zoll erreichen; ist dann dx = 1/100 Zoll, so wird ϱdx = 0,03 Quadratzoll als
correspondirender Fehler in der Fläche. Man sieht hieraus, was dazu gehört, wenn die
Fläche auf einzelne Tausendtheile des Quadratzolles sicher seyn soll. Die Fehler in
x sind also mit besonderer Sorgfalt zu vermeiden,
wenn die Rolle nahe am Rande der Scheibe ist. Die Sicherheit ist größer, wenn die
Rolle während der Meßoperation mehr in der Mitte der Scheibe bleibt.
Der Anfangspunkt ist entweder so zu wählen, daß die Rolle sich nahe in der Mitte der
Scheibe befindet, oder an einer Stelle des Umfangs, welche nahezu y parallel ist, weil in beiden Fällen der Fehler klein
wird, wenn der Endpunkt nicht genau mit dem Anfangspunkte zusammentrifft.
Kleinere Fehler, welche das Auge beim Umschreiben der Figur bemerkt, lassen sich
compensiren, ohne die Arbeit neu anfangen zu müssen. Fährt man z.B. über eine Ecke
der Figur hinaus, so darf man bloß in derselben Linie auf den wahren Punkt
zurückkehren; oder hat die Spitze an einer Stelle einen sichtbaren Flächenfehler
nach außen gemacht, so kann derselbe bei der Fortsetzung durch einen gleichen Fehler
nach innen verbessert werden u.s.w.
Wir haben vom §. 8 bis 14 die Ursachen und die Art ihrer Wirkung kennen
gelernt, welche bei der Anwendung des Apparates Fehler veranlassen, und die Mittel
angegeben, diese Ursachen entweder wirklich zu entfernen, oder durch ein geeignetes
Verfahren unschädlich zu machen. Die bedeutende Anzahl dieser Fehlerquellen könnte
vielleicht einiges Bedenken hinsichtlich der praktischen Anwendbarkeit unseres
Instrumentes erregen. Allein es ist nicht nothwendig, die verschiedenen
Untersuchungen wirklich durchzuführen. Stimmen die Versuche mit den Kreisen auf der
Messingplatte hinreichend überein, und erhält man auch dieselben Werthe bei
verschiedenen Lagen der Rolle auf der Scheibe oder bei mehr oder weniger lang
ausgezogener Stange, so kann man von der Richtigkeit des Apparates versichert seyn.
Durch denselben Versuch überzeugt man sich auch, ob nach einiger Zeit das Instrument
sich verändert habe oder nicht, und wird nöthigenfalls die Angaben desselben gehörig
verbessern.
Die schöne und sinnreiche Idee, welche diesem Instrumente zu Grunde liegt, und seine
überraschende Eigenschaft, das allgemeine Integral ∫f
(x
)dx
in aller Strenge mechanisch darzustellen, was selbst die Mathematik in
unendlich vielen Fällen nur näherungsweise vermag, wird gewiß den Beifall des
mathematischen Publicums erhalten. Noch wichtiger ist der große Gewinn, welcher für
die praktische Anwendung zur Flächenberechnung hervorgeht. Diese Ueberzeugung
sowohl, als der Umstand, daß das Instrument eben erst in die Welt tritt, veranlaßten
mich, dasselbe sorgfältig zu analysiren, um Grundsätze aufzufinden, welche sowohl
beim Baue als dem Gebrauche des Apparates von Nutzen seyn können.
Tafeln