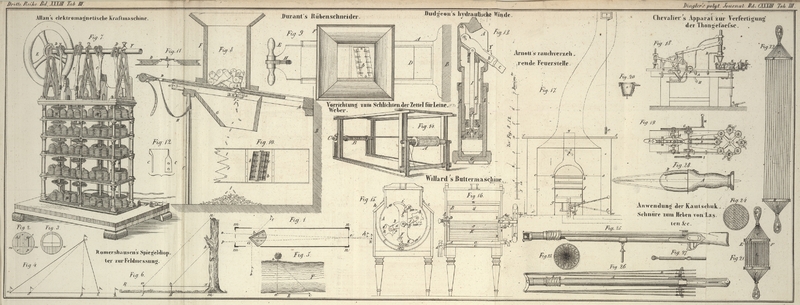
| Titel: | Romershausen's Spiegeldiopter zur Feldmessung. |
| Autor: | Dr. theol. Elard Romershausen [GND] |
| Fundstelle: | Band 133, Jahrgang 1854, Nr. XL., S. 161 |
| Download: | XML |
XL.
Romershausen's Spiegeldiopter zur Feldmessung.
Mit Abbildungen auf Tab.
III.
Romershausen's Spiegeldiopter zur Feldmessung.
Dieses im Jahr 1821 von mir construirte und nachgerade sehr vervollkommnete
WinkelinstrumentRomershausen's Spiegeldiopter, ein neues
mathematisches Instrument für praktische Feldmessung etc. Lithograph. Acken
1821. ist bereits vielfach im Gebrauch bei ökonomischen Messungen und hat sich
dabei, nach dem Urtheil der Sachverständigen, als das hülfreichste und sicherste
bewährt. Um daher die allgemeinere Benutzung desselben zu fördern und namentlich die
Mechaniker zu richtiger Ausführung desselben in Stand zu setzen, sehe ich mich bei
der unrichtigen Darstellung einiger neueren Schriftsteller veranlaßt, folgende
berichtigende Mittheilung zu machen:
I. Beschreibung des
Spiegeldiopters.
Eine Messingplatte Fig. 1, m, m, n, n, 6'' rheinl. lang und 1''
breit, bildet die Basis des Instruments. An beiden Enden dieser Platte bei m, m und n, n werden die
Diopterscheiben Fig.
2 und 3, bei den entsprechenden Linien m m und n n senkrecht und concentrisch festgelöthet. Beide
Scheiben haben einen Durchmesser von 1 1/4 Zoll.
Das Oculardiopter Fig. 2 ist mit den beiden parallelen, bis auf die Tragplatte
herablaufenden, feinen Sehschlitzen o und p versehen, wovon o mit
45° und p mit 90° bezeichnet ist.
Das Objectivdiopter Fig. 3 bildet bis zu der Linie n n herab
einen offenen Rahmen, in welchem das aus feinem Silberdraht bestehende Fadenkreuz
ausgespannt ist.
Auf der Tragplatte Fig. 1 werden die beiden feinpolirten, 4 Linien hohen Metallspiegelchen
a und b vollkommen
senkrecht und um der größern Uebersicht willen nahe an dem Ocular angebracht. Diese
Spiegel halbiren das Sehfeld, so daß über dieselben hinweg eine freie Durchsicht zu
dem Fadenkreuz des Objectivs stattfindet.
Nach optischen Grundsätzen wird die Spiegelfläche a in
dem Winkel = 45° gegen die Visirlinie p e
geneigt, damit ein außerhalb von der Seite einfallender Strahl d a, dem in p beobachtenden
Auge nur alsdann sichtbar wird, wenn er mit der Visirlinie p
e h auf das genaueste einen rechten Winkel bildet. Also
< p a d = < d a h = 90°.
Eben so schneidet die Spiegelfläche b die Visirlinie o k in einem Winkel = 22 1/2°, damit der von
außen einfallende Strahl c b nur alsdann zu dem Auge des
Beobachters in o gelangt, wenn derselbe mit der
Visirlinie o e k, im Durchschnittspunkt b, einen Winkel = 45° bildet. Also
< c b k = 45°,
mithin
< c b o = 135°.
Nachdem beide Spiegel für diese Winkelrichtungen auf das sorgfältigste rectificirt
sind, werden sie nicht allein auf der Tragplatte festgeschroben, sondern auch zum
Schutz gegen jede mögliche Verrückung, auf derselben verlöthet.
Zur Aufnahme und zu vollkommenem Schutz dieser Vorrichtung wird nun ein leichtes
Messingrohr gefertigt, welches nach allen seinen Dimensionen dazu passend, nach
Einfügung derselben durch die concentrischen Diopter m
und n dicht geschlossen ist. Dieses Rohr erhält zu
beiden Seiten für die Spiegel a und b zwei Fensteröffnungen, welche bis zur Bodenplatte
herabreichen und etwas höher als die Spiegel sind. Das Objectivdiopter wird durch
ein Planglas geschützt und beide Enden des Rohres werden mit einer ringförmigen
Schraubenfassung dicht verschlossen. Das Instrument gleicht demnach einem kleinen 6
Zoll langen und 1 1/4 Zoll im Durchmesser haltenden Taschenfernrohr, und kann bequem
und ohne irgend eine Beschädigung in der Tasche geführt werden.
II. Die Behandlung und Beobachtungen des
Spiegeldiopters.
Das Instrument wird ohne Stativ in freier Hand geführt, indem man dasselbe an einen
Meßstab anlehnt, welcher alsdann zur Bezeichnung der gefundenen Winkelpunkte
dient.
Sieht man vermittelst des Diopters für den 90sten Grad unter Einvisirung des
Objectivfadens e (Fig. 1) über den Spiegel
a hinweg, nach irgend einem entfernten Gegenstand,
hier nach dem Stab h hin, so erblickt man genau unter
demselben im Spiegel a das reflectirte Bild eines zur
Seite liegenden Gegenstandes, hier des Stabes d, wenn
derselbe, wie es hier der Fall ist, im Standpunkt des Beobachters mit dem
unmittelbar gesehenen Stab h auf das genaueste einen
rechten Winkel bildet, also die Linie a d senkrecht auf
p h steht.
Auf der andern Seite erfolgt dieses eben so bei dem Diopter des 45sten Grades. Der
direct gesehene und mit e einvisirte Stab k bildet im Schnittpunkt b
des Spiegels mit dem reflectirten Stabe c den Winkel k b c = 1/2 Rechter = 45°.
Da die Einrichtung des Spiegeldiopters eine weite Uebersicht des Terrains gestattet,
so ist die Absteckung dieser Winkelrichtungen leicht ausführbar, wenn der Geometer
bei Einvisirung des Objectivfadens auf den vorliegenden Stab den Spiegel im Auge
behält, bis der in der Gegend von d oder o befindliche Gehülfe in demselben erscheint und zur
richtigen Einsetzung seines Stabes angewiesen wird. Die mathematisch genaue
Feststellung dieser Richtungsverhältnisse ist bei der scharfen und unwandelbaren
Rectification des Instruments leicht und vollkommen ausführbar, indem sich das Bild
des reflectirten Stabes bei der Beobachtung an den über den Spiegel hinweg
unmittelbar gesehenen Stab so genau anschließt, daß beide ein Ganzes auszumachen
scheinen.
Um beide Diopter sowohl rechts als links zur Bestimmung dieser Winkelrichtungen zu
gebrauchen, darf man das Instrument nur umkehren, so daß die Spiegel oben und die
freie Durchsicht zum Objectiv nach unten liegt.
Auch reducirt das Spiegeldiopter seine Messungen stets selbst auf die
Horizontalebene, indem die senkrecht aufgestellten Stäbe k und h mit den gleichfalls senkrecht
stehenden reflectirten Stäben d oder c nur dann geradlinig aneinander schließen, wenn die
Visirlinie im Horizont liegt. Ist daher einer der Punkte c,
d, h oder k zu hoch oder zu tief gegen den
Standpunkt des Beobachters, so wird die Richtung desselben durch einen im Alignement
eingesetzten Stab bemerkt, welchen wir in der Folge mit R bezeichnen wollen.
III. Allgemeine Leistungen des
Spiegeldiopters.
Da der Raum eine vollständigere Darstellung der Messungen hier nicht gestattet, so
verweise ich in dieser Beziehung auf die diesen Gegenstand näher erörternden SchriftenRomershausen's Spiegeldiopter und Längenmesser
etc. Halle 1845. Desselben Meßkunde für Landleute
etc. Halle 1847.Hauptmann Helmuth, die Distanzmessung der
Artillerie und das militärische Croquiren mit Hülfe des Romershausen'schen Längenmessers etc. Halle 1848,
S. 57. (In Beziehung auf militärische Zwecke.) und bemerke nur im Allgemeinen, daß das Spiegeldiopter die Factoren zur
Flächenberechnung und zum Entwurf unmittelbar auf dem Felde gibt. Wir wollen dieses
an dem einfachen Beispiel Fig. 4 näher erörtern.
Um in der Grunglinie a b des ∆ a b c den Punkt p zu
bestimmen, wo das Höhenperpendikel c p einfällt, läßt
der Geometer zu seiner Führung im Alignement von a b
einen Richtungsstab R aufstellen. Er schreitet auf a b vorwärts, indem er den Objectivfaden des
Rechtwinkeldiopter auf b R richtet, bis ihm im Punkt p der Stab c im Spiegel
erscheint und mit den sich deckenden Stäben b R als ein
Ganzes erscheint und bezeichnet diesen Punkt. Nach Messung der Basis a b und Höhe p c ergibt sich
nun sofort der Flächeninhalt:
F = (ab × pc)/2.
Noch einfacher und namentlich bei coupirtem Terrain sicherer ist diese Messung, wenn
der Geometer auf der Basis a b vermittelst des Diopters
des 45sten Grades das rechtwinkelig-gleichschenkelige ∆ d p c errichtet. Er erhält hier die Factoren des
Flächeninhaltes des ∆ a b c, ohne die Grundlinie
zu verlassen; denn da die Katheten d p = p c, so ist:
F = (ab × dp)/2.
Durch diese Construction des rechtwinkelig-gleichschenkeligen ∆ ergibt
sich also auch auf einfachste Weise das Maaß unzugänglicher Linien und Entfernungen,
wie z.B. die Breite a b des Flusses F, Fig. 5, wo also: die
Breite a b = a c am
diesseitigen Ufer.
Ebenso gestattet endlich der aufwärts gerichtete Spiegel des Diopters des 45sten
Grades eine schnelle und sichere Messung senkrechter Höhen und Höhenabschnitte, wie
dieses Fig. 6
anschaulich macht. Wenn hier x m = a l die bemerkte Augenhöhe des Beobachters über dem
Boden ist, so ist nach Construction des ∆ a x n
die Höhe des Baumes m n = a x + x m und
da a n # b
h, so ist:
der gesuchte Höhenabschnitt h n = a b.
Diese und mehrere ähnliche hülfreiche Leistungen des Spiegeldiopters bedürfen für den
Sachverständigen keiner weitern Erörterung; sie gewähren, wie sich Jeder überzeugen
wird, bei der unwandelbaren und scharfen Winkelbestimmung des Instruments
vollkommne, der unmittelbaren Messung nicht nachstehende, mathematische
Genauigkeit.
––––––––––
Der alte Adam'sche Winkelspiegel gewährt dagegen,
abgesehen von seiner unbequemen Form und Beobachtungsweise, nicht die Hälfte dieser
Leistungen. Er gibt nur den rechten Winkel und ist bei den auf einem federnden
Metallblech angebrachten Glasspiegeln so unsicher und wandelbar in seiner
Rectification, daß dieselbe vor jedesmaligem Gebrauch mit vielem Zeitverlust
revidirt und regulirt werden muß.
––––––––––
Bei den wesentlichen und allgemein anerkannten Vorzügen des Spiegeldiopters empfehle
ich dasselbe den praktischen Feldmessern und wünsche umsomehr die Mechaniker durch
obige Darstellung zu richtiger Anfertigung desselben in Stand zu setzen, da Barfuß in der so eben erschienenen 3ten Auflage seines
HandbuchsDr. Barfuß, Handbuch
der höhern und niedern Meßkunde. 3te Auflage. Weimar 1854, S. 163. eine völlig unrichtige und nicht im entferntesten ähnliche Beschreibung
desselben gibt. Er vergleicht das Spiegeldiopter mit dem völlig heterogenen Fallon'schen Spiegellineal und entwirft davon eine völlig
entstellende Zeichnung. Nach ihm sollen die Diopter meines Instruments durch zwei
messingene Stifte gebildet und die Vorrichtung selbst in einem viereckigen Gehäuse
angebracht seyn u.s.w. Er hat hiernach das Spiegeldiopter offenbar weder gesehen
noch geprüft, sondern auch dießmal die vorliegende fingirte Beschreibung wörtlich
von Schneitler
Die Instrumente und Werkzeuge der höhern und niedern Meßkunst etc. von Schneitler. Leipzig 1848, S. 56. abgeschrieben, welcher bereits wegen mehrerer anderer Compilationen und
Verfälschungen sowohl in dieser Zeitschrift, als auch in Beziehung auf meine
Instrumente, von einem unserer ausgezeichnetem Mathematiker öffentlich zurecht
gewiesen wurde.Archiv der Mathematik und Physik von Grunert, Th.
XIII H. 2,1849, S. 162 und Th. XII H. 2, S. 638.
B. hätte daher besser gethan, in feinem sonst sehr instructiven Werke das ihm
unbekannte Spiegeldiopter, wie mehrere andere neuere MeßinstrumenteUeber den Reichenbach'schen Distanzmesser und Romershausen's Längenmesser, polytechn, Journal
Bd. CXVI S. 352.mit Stillschweigen zu übergehen, als vorliegende Unrichtigkeiten zu
verbreiten. Die Beurtheilung dieses Mißgriffs überlasse ich seiner eigenen bessern
Einsicht.
Marburg, im Juni 1854.
Dr. Romershausen.
Tafeln