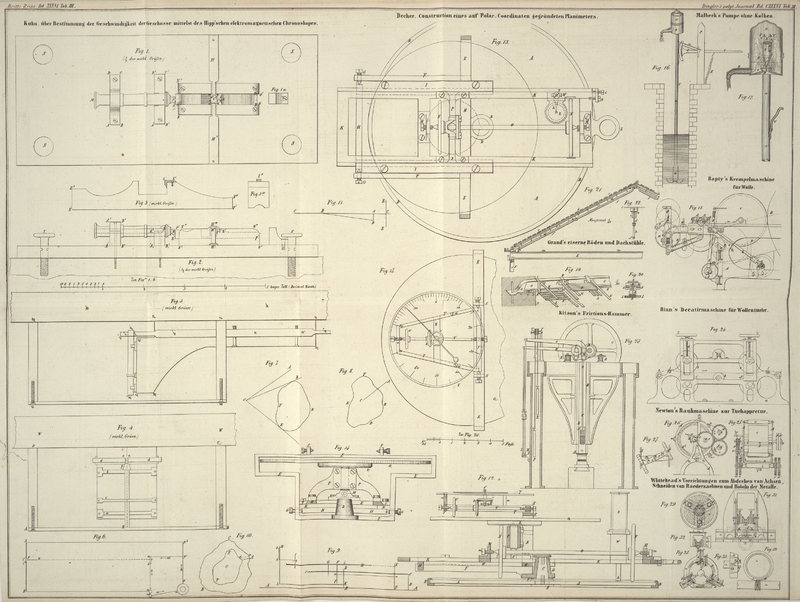
| Titel: | Theorie und Construction eines neuen, auf Polar-Coordinaten gegründeten Planimeters; von Professor G. Decher. |
| Autor: | Georg Decher [GND] |
| Fundstelle: | Band 136, Jahrgang 1855, Nr. XLI., S. 168 |
| Download: | XML |
XLI.
Theorie und Construction eines neuen, auf
Polar-Coordinaten gegründeten Planimeters; von Professor G. Decher.
Mit Abbildungen auf Tab.
III.
Decher, Beschreibung eines neuen Planimeters welches auf
Polar-Coordinaten gegründet ist.
Beim Durchlesen der im polytechn. Journal Bd. CXVI
S. 424 u. f. mitgetheilten Beschreibung des Planimeters von Wetli erwachte in mir sogleich das Bedenken, ob nicht die
drehende Wirkung, welche die den Stift führende Hand beim Nachfahren des Umfanges
der zu berechnenden Figur auf den Wagen oder Schlitten ausübt, und welche bald
vorwärts bald rückwärts
gerichtet ist, nach und nach eine tobte Bewegung erzeugen müsse, welche der
Genauigkeit des Instrumentes bedeutenden Eintrag thun dürfte; dieser Zweifel legte
mir den Gedanken nahe, daß der betreffende Uebelstand bei einem auf
Polar-Coordinaten gegründeten Instrumente, bei welchem
alle Bewegungen nur um oder gegen eine feste verticale Achse stattfänden,
vermieden werden könne, und veranlaßte mich, weiter über die Construction eines
solchen Instrumentes nachzudenken. Die Theorie desselben war bald festgestellt und
der darauf gegründete Entwurf versprach zugleich ein einfacheres und für viele Fälle
zweckmäßigeres Instrument als das von Wetli construirte;
ich wollte aber darüber nichts veröffentlichen, bis ein solches ausgeführt sey und
ich Versuche damit angestellt hätte. Die seitdem durch Prof. Dr. Bauernfeind bekannt gemachte complicirtere
Einrichtung, welche Hr. Hofrath Hansen dem Wetli'schen Planimeter geben zu müssen glaubte, um
dasselbe möglichst zuverlässig zu machen, war nicht geeignet, mich von meinem
obengenannten Bedenken zu befreien und meinen Glauben an die Vorzüge meines
Instrumentes, namentlich in Betreff der Einfachheit, Zweckmäßigkeit und
Bequemlichkeit in der Anwendung wankend zu machen, und diesem Glauben möge man es zu
gut halten, wenn ich meinem frühem Vorsatz untreu werde und die beabsichtigte
Einrichtung meines Instrumentes vor der noch in ziemlicher Ferne stehenden
Ausführung veröffentliche, in der Hoffnung, daß sich ein Mechaniker finden werde,
welcher dasselbe der Ausführung werth hält.
Betrachten wir zunächst die Theorie des Instrumentes. Die Polar-Coordinaten in
der Ebene bestehen bekanntlich in dem Fahrstrahl CM =
r, Fig. 7, welcher die
Entfernung eines Punktes M von dem Pol oder der zur
Ebene senkrechten Achse C mißt, und aus dem Winkel ACM = ω, welchen der
Fahrstrahl CM mit einer in der Ebene gezogenen
fixen Geraden CA einschließt. Ferner hat man für
die Fläche O₁ des Sectors CBDEC den Ausdruck:
Textabbildung Bd. 136, S. 169
worin α₀ und α₁ die Winkel ACB und ACE der begränzenden
Fahrstrahlen CB und CE mit der Geraden AC bedeuten und r₁ durch die Gleichung:
r₁ = f₁ (ω)
der begränzenden Curve BDE
in Function von ω gegeben vorausgesetzt wird.
Ebenso hat man für die Oberfläche O₀ des Sectors
CBFEC den Werth;
Textabbildung Bd. 136, S. 170
worin nun die Curve BFE
durch die Gleichung:
r₀ = f₀ (ω)
ausgedrückt gedacht wird. Für die Fläche O der geschlossenen Figur BDEF, welche den Pol C nicht einschließt,
findet man demnach den Ausdruck:
1) Textabbildung Bd. 136, S. 170
Schließt die zu berechnende Figur dagegen den Pol C ein,
wie in BDEF, Fig. 8, und ist nun
r = f (ω)
die Gleichung ihrer Begränzung, so hat man einfach
2) Textabbildung Bd. 136, S. 170
als Ausdruck für ihre Oberfläche.
Sey nun AA, Fig. 9, eine horizontale
Ebene, auf welcher wir die zu berechnende Figur aufgetragen annehmen wollen, BB eine dazu senkrechte feste Achse, CC eine unbiegsame Gerade, welche sich sowohl um
die Achse CC drehen, als auch durch dieselbe in
der Richtung ihrer Länge verschieben läßt, und welche an einem Ende den Stift D trägt, der dem Umfang der auszumessenden Figur folgen
soll; E, E und F, F seyen
zwei vertical-stehende Räder, welche auf derselben Achse a, a befestigt sind und mit dieser Achse in Bezug auf
die Gerade CC eine unveränderliche Lage behalten;
das erstere und etwas größere von beiden stützt sich auf die Ebene AA und wälzt sich auf dieser ab, wenn die Gerade
CC um BB
gedreht wird; auf dem kleinern F, F dagegen ruht die
horizontale Scheibe H, H, welche sich um die auch in der
Geraden CC befestigte und allen Bewegungen
derselben folgende Achse G dreht, mit hinreichendem
Drucke so auf, daß sie vermöge der Reibung durch das Rad F,
F umgedreht wird; endlich sey J, J ein
vertical-stehendes Rädchen, welches wieder auf der Scheibe H, H ruht, dessen Achse b, b
aber so mit dem Träger K, L, M verbunden ist, daß sie
mit der Geraden CC und den übrigen Achsen BB, aa und G in derselben Vertical-Ebene liegt, und daß sie
zwar auch wie die a, a an der drehenden Bewegung der
Geraden CC Theil nimmt, daß sie aber in Bezug auf B, B keine Verschiebung erleiden kann, daß also das
Rädchen J, J immer in derselben Entfernung von BB bleibt. Es wird dann einleuchten, daß der ganze
Apparat auf der Achse B, B ruhend sich mit dem Stifte
D um diese Achse dreht, daß die Räder E, E und F, F, die Scheibe
H, H und das Rädchen J,
J in Bezug auf ihre Achsen in Ruhe bleiben, wenn der Stift D längs einer durch B
gehenden Geraden oder längs eines constanten Fahrstrahls geführt wird, daß dagegen
eine drehende Bewegung dieser Theile des Apparates um ihre Achsen eintritt, sobald
der Stift D sich um die Achse B,
B bewegt oder einen Winkel Δω um den Pol B beschreibt, da
sich alsdann das Rad E, E auf der Ebene AA abwälzt, also sich und das Rad F, F und die auf ihm ruhende Scheibe H, H und diese wieder das Rädchen J, J umdreht; und die Aufgabe besteht nun darin, diese Bewegungen so
einzurichten, daß der auf der Achse des Rädchens J, J
sitzende Zeiger Z beim Umfahren der zu berechnenden
Figur einen Winkel Δϕ beschreibt,
welcher der Fläche dieser Figur proportional ist.
Bezeichnen wir dazu die Entfernung des Stiftes G von der
Achse B, B oder die Länge des Fahrstrahls mit r, die Halbmesser der Räder E,
E und F, F mit h₁ und h₂, den unveränderlichen
Abstand ED der Ebene des Rades E, E von dem Stifte D mit
a, die gleichfalls unveränderlichen Abstände GF und GE der
Räder F, F und E, E von der
Achse G der Scheibe H, H mit
h₃ und b, ferner
die constante Entfernung Ji des Rädchens J, J von der festen Achse BB mit c und den Halbmesser dieses Rädchens
mit h₄, so haben wir zuerst
BE = r – a, GJ = r +
c – (a + b).
Nehmen wir dann r einen Augenblick als constant an und
drehen die Gerade CC um den Winkel Δω, so wälzt das Rad E, E den Bogen (r –
a) Δω ab,
es dreht sich also dabei um den Winkel
Δψ₁ = (r – a)/h₁ Δω,
ebenso wie das Rad F, F, von
welchem deßhalb ein Punkt des Umfanges den Bogen
h₂Δψ
₁ = h₂/h₁ (r – a) Δω
zurücklegt. Der Berührungspunkt F
dieses Rades und der Scheibe H, H beschreibt denselben
Bogen und die letztere dreht sich um den Winkel
Δψ₂ = h₂/h₃ Δψ₁ = h₂/h₃ . (r – a)/h₁ Δω;
der Berührungspunkt J der Scheibe
und des Rädchens J, J beschreibt darnach den Bogen
(r + c
– (a + b)) Δψ₂ = h₂/h₃ (r – a)/h₁ (r + c
– a – b) Δω
und das Rädchen selbst dreht sich um den Winkel
Textabbildung Bd. 136, S. 172
Daraus ergibt sich das Verhältniß der Aenderung von ϕ in Bezug auf die Aenderung von ω
Textabbildung Bd. 136, S. 172
welches für ein veränderliches r
in das nur für eine augenblickliche Lage und Größe von r
geltende Aenderungsgesetz
3) Textabbildung Bd. 136, S. 172
übergeht, worin man sich nun r als
eine Function von ω zu denken hat. Macht man
demnach noch
4) c – b – a = a oder c = b + 2a,
so wird einfach
5) Textabbildung Bd. 136, S. 172
Bewegt sich also der Stift D längs der Curve BDE, Fig. 7, so dreht sich der
Zeiger Z um einen Winkel
Textabbildung Bd. 136, S. 172
folgt der Stift dann aber der Curve EFB, so geht der Zeiger um einen Winkel
Textabbildung Bd. 136, S. 172
zurück, und zeigt am Ende, wenn der Stift wieder in B angekommen ist, noch eine Drehung
Textabbildung Bd. 136, S. 172
oder
6) Textabbildung Bd. 136, S. 173
Dieser Ausdruck, verglichen mit dem Werthe (1) für die Fläche
O dieser Figur gibt die Beziehung:
7) Textabbildung Bd. 136, S. 173
und zeigt, daß die Fläche einer Figur,
welche den Pol
C (die Achse B, Fig. 9) nicht einschließt, unabhängig von der Constanten
a
unmittelbar durch den Drehungswinkel des Zeigers gemessen
wird.
Schließt dagegen die Figur welche berechnet werden soll, die Achse B oder den Pol C, Fig. 8, ein, so
wird sich der Zeiger fortwährend in demselben Sinne drehen und zwar, während der
Stift den ganzen Umfang der Figur beschreibt, um einen Winkel
Textabbildung Bd. 136, S. 173
Dieser Werth, verglichen mit dem Werthe (2) für die Fläche O der betreffenden Figur, gibt die Gleichung
8) Textabbildung Bd. 136, S. 173
man hat daher in diesem Falle, um die FlächeOzu erhalten, zu der Angabe des Zeigers noch die constante
Kreisfläche πa
² zu addiren, welche sich durch Versuche
leicht finden läßt, wenn man ein und dieselbe Figur einmal nach der ersten Art
ausmißt, d.h. so, daß die Achse B außerhalb der Figur
liegt, und dann nach der zweiten Art, indem man diese Achse in die Figur hinein
versetzt.
Der Werth von O wird dagegen wieder unabhängig von a, wenn die zu berechnende Figur von zwei geschlossenen
Linien begränzt wird und beide den Pol C einschließen,
wie in Fig.
10, wobei man aber der innern Linie mit dem Stift im Sinne der negativen
ω folgen, die Figur also in der Richtung ABCADEFDA umfahren muß, gerade so, als wenn bei
AD eine Unterbrechung des ringförmigen Raumes
wäre, in welchem Falle die Figur nur in der Richtung ABCadEFDA umfahren werden kann.
Nach dem Vorhergehenden ist die Angabe des Instrumentes unabhängig von den Größen c und b; diese stehen aber
unter sich und zu der Größe a in einer durch die Gleichung (4) ausgedrückten
Abhängigkeit, durch welche die Einrichtung des Instrumentes bedingt wird und zwar in
Verbindung mit den andern Bedingungen, daß das Rädchen J,
J immer auf der Scheibe H, H aufliegen muß, und
daß der Stift D nicht unter diese Scheibe kommen darf.
Bezeichnet man nun den größten Werth von r, d.h. die
größte Entfernung des Stiftes D von der Achse BB, mit R, so erhält
man als größten Abstand des Rädchens von der Achse G der
Scheibe den Werth: R + c
– a – b, oder
mit der Bedingungsgleichung (4) den Werth: R + a, welcher nach den ersten der genannten Bedingungen
zugleich die Größe des Halbmessers der Scheibe vorstellt. Darnach erhält aber diese
Scheibe, auch wenn man a möglichst klein macht, eine
ziemliche Größe im Vergleich zu der Größe der Figuren, für welche das Instrument
anwendbar ist. Es dürfte daher zweckmäßiger seyn, die Größe a negativ zu machen, d.h. den Stift D zwischen
die Achse B, B und das Rad E,
E zu setzen; man hat dann
BE = r + a, c = b
– 2a, GJ = r – a,
also noch wie früher (Gleichung 5)
Textabbildung Bd. 136, S. 174
der Halbmesser H der Scheibe wird
dadurch R – a, und
das Instrument kann überhaupt für gleiche Größe der Anwendbarkeit eine geringere
Ausdehnung erhalten; denn wenn auch durch die ebengemachte Annahme und die zweite
der obigen Bedingungen die Größe b so beschränkt wird,
daß sie nicht kleiner werden kann, als H + a oder kleiner als R, so
wird doch dadurch c nicht viel größer als R – a.
Durch die vorhergehende Annahme in Betreff der Größe a
entsteht aber die neue Schwierigkeit, daß der Stift D
oder die ihn ersetzende optische Achse der Loupe durch die Achse a, a der Räder E, E und F, F gehen müßte; diese Schwierigkeit läßt sich indessen
leicht heben, wenn man beachtet, daß der Stift D nicht
nothwendig in der durch BB und CC gehenden Ebene liegen muß. Denn ist D, Fig. 11, die
Horizontalprojection des Stifts, B die der festen Achse,
also BD der Fahrstrahl r, und bezeichnet man die Projection Bd
dieses Fahrstrahls auf die Gerade CC' mit r' und die constanten Entfernungen dC' und dD mit
a und f, so hat man nach
dem Frühern
9) Textabbildung Bd. 136, S. 174
es ist aber auch
r'² = r²
– f²
und daher wird im jetzigen Falle
10) Textabbildung Bd. 136, S. 175
Für eine geschlossene Figur, welche den Pol nicht einschließt, bleibt also die
frühere Gleichung
11) Textabbildung Bd. 136, S. 175
für eine solche aber, welche den Pol einschließt, wird
Textabbildung Bd. 136, S. 175
oder wenn man
Textabbildung Bd. 136, S. 175
setzt
12) O = kΔϕ + πl²;
es ändert sich also gegen die frühere Annahme nichts, weil die
Fläche πl² ebenso wie πa² durch den Versuch bestimmt
werden muß.
Endlich wäre noch das Instrument so einzurichten, daß der oben mit k bezeichnete Coefficient, welcher die von der
Winkel-Einheit (57°,29..) repräsentirte Fläche ausdrückt, nicht zu
groß wird, damit der der Flächeneinheit entsprechende Winkel Δϕ nicht zu klein ausfällt. Theilt
man, wie es am zweckmäßigsten ist, das Zifferblatt in 100 gleiche Theile und drückt
den Winkel Δϕ durch n solcher Theile aus, so hat man
Δϕ = 2π/100 n
und damit wird
13) O = h₃h₄ h₁/h₂ π/100 n;
für die einem solchen Theile entsprechende Fläche ergibt sich
also der Werth
14) f
= h₃h₄ h₁/h₂ π/100 n
und dieser wird, da h₁/h₂ immer größer als 1 werden muß, um so kleiner,
je kleiner h₃ und h₄ sind, d.h. je näher das Rad FF an
der Achse G der Scheibe H,
H, und je kleiner das Rädchen J, J ist.
Diesen Bemerkungen gemäß beabsichtige ich, dem Instrumente die in den Figuren 12 bis 15
dargestellte Einrichtung zu geben.
A ist eine kreisförmige ebene Scheibe von starkem
Spiegelglase, welche in einen messingenen Ring B gefaßt
und in der Mitte kreisförmig durchbohrt ist, um hier die conische Achse C befestigen zu können, und zwar mittelst der Schraube
g, deren Kopf zugleich als Stütze für die Mitte der
Scheibe A dient, wenn dieselbe auf die Ebene aufgesetzt
wird, auf welcher die zu berechnende Figur gezeichnet ist. Auf der Achse C und zum Theil von der Feder p getragen, dreht sich die conische Hülse D
mit dem Träger E, in welchem der ganze übrige Theil des
Instrumentes ruht. Dazu besitzt derselbe zwei horizontale Arme F und in den Enden derselben die conisch zugespitzten
Schrauben G, welche eine horizontale Drehungsachse für
den Rahmen H bilden, so daß sich dieser um dieselbe
zwischen dem Träger E passend auf und nieder bewegen
läßt. Auf diesen Rahmen H sind die abgeschrägten Leisten
J aufgeschraubt, welche dem an seinen Seiten in
gleicher Weise abgeschrägten Rahmen K zur Führung dienen
und demselben eine leichte aber sichere Verschiebung in der Richtung seiner Länge
gestatten. In der Mitte dieses Rahmens K (der Breite
nach) sind die kleinen Träger M befestigt, deren
Schrauben m der Achse O mit
den Rädern N und N' als
Drehungspunkte dienen; das Rad N ist etwas größer im
Durchmesser als N' und ruht auf der Ebene A auf und zwar mit einem Drucke, welcher hinreichend
seyn dürfte, um die gleitende Bewegung des Rades N auf
der Scheibe A zu verhindern, wenn der Rahmen K um die Achse C gedreht
wird, da sich das Gewicht der Rahmen H und K und der darauf befestigten Theile nur auf die Achse
G, G und das Rad N
vertheilt, und nach unserer Einrichtung die Länge der Arme F schon wegen des nöthigen Spielraumes für die Bewegung des Rades N' so bemessen ist, daß der Schwerpunkt aller dieser
Theile immer zwischen die Achse G, G und das Rad N fällt, auch wenn dieses bis an die Hülse D hin verschoben wird. Man könnte indessen, um in dieser
Beziehung vollkommen sicher zu seyn und zugleich zu verhindern, daß die
Spiegelscheibe A bei der nach der Länge des Rahmens K stattfindenden Verschiebung des Rades N verkritzt werde, dieses letztere auf dem Umfange mit
einem sehr dünnen Ueberzug von feinem Leder oder Kautschuk bekleiden; ich für meinen
Theil habe indessen die Ueberzeugung, daß bei dem stattfindenden Drucke das Rad N auch mit blanker Metallfläche nicht gleitet, wenn der
Rahmen K stetig um C gedreht
wird.
Auf dem Rahmen K ist ferner der Träger P aufgeschraubt, welcher das Lager für den cylindrischen
Zapfen der kreisförmigen ebenen Scheibe Q enthält; diese
Scheibe ist unterhalb noch durch eine kleinere ebene Scheibe R verstärkt und ruht mittelst dieser auf dem Rade N', auf das sie mit ihrem ganzen Gewichte drückt, und dadurch wieder
hinreichende Reibung erzeugt, um ein vollkommenes Abwälzen zwischen beiden zu bewirken, auch wenn die
Scheibe R eine blanke Metallfläche darbietet, welche
ebenso wie die obere Ebene der Scheibe Q nur fein
abgeschliffen und nicht polirt zu seyn braucht.
Endlich ist auf dem Rahmen K, welcher vorn in den
ringförmigen Griff L zur Führung desselben endigt, noch
der Träger W für die vertical stehende Loupe Z befestigt, und zwar so, daß die Schraube q durch einen länglichen Schlitz hindurchgeht, und der
Träger W sich mittelst der Druck- und
Zugschrauben i und k nach
der Länge des Rahmens K etwas verschieben läßt, um der
Bedingungsgleichung (4) in der Form:
a = (c – b)/2
durch Correction der Größe a so
genau wie möglich genügen zu können. Der Träger W ist
nach unten bis nahe an die Scheibe A hin verlängert und
trägt dort eine horizontale, bis in die Achse der Loupe reichende feine Stahlspitze
h, welche die Gestalt eines längs seiner Achse
durchschnittenen Kegels hat, und den ebenen Achsenschnitt der Scheibe A zuwendet, und deren äußerste Spitze beim Gebrauch des
Instrumentes auf der zu berechnenden Figur herumgeführt wird. Statt dieser Spitze
kann indessen, wenn man es vorzieht, eben so leicht ein mit einem kleinen Ringe
versehenes Glasplättchen angebracht werden; am besten dürfte es aber seyn, um jede
Parallaxe zu vermeiden (bei der von Hansen angewendeten
freien Loupe ohne begränzte Ocularöffnung scheint mir dieselbe ziemlich groß werden
zu können), statt der einfachen Loupe ein nur aus Objectiv und Ocular
zusammengesetztes Mikroskop von nicht starker Vergrößerung anzubringen und den
Index, Stahlspitze oder Glasplättchen mit Ring, wie gewöhnlich zwischen dem Objectiv
und Ocular zu befestigen, wobei aber das Centriren dieses Index nothwendig und die
Loupe wieder complicirter wird.
Der Träger E geht über die Scheibe Q hinweg und besitzt über derselben zwei Ansätze S mit Schrauben, von deren Spitzen der Rahmen T festgehalten wird mit der Freiheit, sich um diese Spitzen wie um eine
horizontale Achse zu drehen; in der Mitte dieses Rahmens dreht sich, ebenfalls in
Spitzen laufend, die Achse V, auf welcher das wie die
Räder N und N' am Rande
abgerundete Rädchen U und das etwas kleinere gezahnte
conische Rädchen b befestigt sind, und über demselben
Rahmen liegt, auf drei Stützen a befestigt, das
Zifferblatt Y. Die Zeigerachse f ruht in einer auf dem Rahmen T befindlichen
Querleiste X und trägt ein conisches Rädchen c, von gleicher Größe wie b,
in welches dasselbe eingreift, so daß der Zeiger mit dem Rädchen U in derselben Zeit einen Umgang macht. Der Druck des Rahmens T und der daran befestigten Theile vertheilt sich auf
das Rädchen U und die Achse i,
i nahezu gleich und bewirkt wieder die zur wälzenden Bewegung des Rädchens
U erforderliche Reibung. Endlich bietet jener Rahmen
und das darauf befestigte Zifferblatt Raum und Stützpunkte genug, um das Zeigerwerk
noch weiter und in der Art zu vervielfältigen, daß man auch die Anzahl der
Umdrehungen des Zeigers ablesen kann.
Nach dieser Beschreibung und der vorausgehenden Theorie des Instrumentes wird es kaum
nothwendig seyn, über dessen Anwendung etwas Weiteres zu sagen; es mögen daher noch
folgende Bemerkungen erlaubt seyn.
Wenn das Instrument in der Größe der Zeichnung ausgeführt wird, so kann der Rahmen
K oder die Loupe eine geradlinige Bewegung von 6,5
Centim. erhalten und damit die Fläche einer Figur berechnet werden, welche in einen
Kreis von 13Cm. Durchmesser beschrieben
ist, wenn die Achse C über den Mittelpunkt dieses
Kreises gestellt wird; es beträgt daher die größte Fläche, welche damit berechnet
werden kann, etwa 130 □Cm.. Die in
dem Entwurfe angenommenen Maaße, welche auf die Angabe des Instrumentes Einfluß
haben, sind
h₁= 20mm, h₂ = 18mm, h₃ = 9mm,
h₄ = 3mm,98;
man hat daher nach (13) und (14)
O = (20 . 9 . 3,98)/(18 . 100) πn□mm = 1,25 n□mm;
f = 1,25 □mm;
ein Theil des Zifferblattes entspricht also einer Fläche von 1
1/4 □mm, oder ein Umgang des Zeigers
einer Fläche von 125 □mm = 1 1/4
□Cm.. Würde man das Instrument
in der doppelten Größe ausführen und alle Verhältnisse beibehalten, so würde die
Fläche f viermal so groß, also
f = 5 □mm,
bei einer größten berechenbaren Fläche von 500 □Cm.
Gegen das Planimeter von Wetli oder Hansen steht das meinige in einem Nachtheil, welcher auf den ersten
Anblick vielleicht nicht unwesentlich genannt werden möchte, und welcher darin
besteht, daß die richtige Angabe des Instrumentes an die genaue Erfüllung der
Bedingung (4) gebunden ist. Wenn diese Bedingung nicht genau erfüllt ist, wenn man
hat
r + c – b + a = r – a + δ statt r –
a
so wird
dϕ/dω = 1/k (r² – a²) + 1/k (r + a) δ
und
Textabbildung Bd. 136, S. 179
oder
Textabbildung Bd. 136, S. 179
der Fehler γ in der Angabe
des Zeigers ist also im ersten Falle, wo der Pol außerhalb der Figur liegt,
Textabbildung Bd. 136, S. 179
im zweiten, wo er von der Figur eingeschlossen wird,
Textabbildung Bd. 136, S. 179
und daher offenbar am größten, wenn r constant ist und seinen größten Werth R hat;
dieser größte Fehler ist demnach
Γ = 2π
δ/k (R + a);
setzt man in diesen Ausdruck die obigen unserer Construction
zu Grunde liegenden Maaße und noch R = 65mm, a = 10mm, und drückt Γ in Theilen des Zifferblattes aus, so wird
Γ = 100/2π .
(18 . 2π)/(10 . 9 . 3,98) . 75 δ = 188,4 δ,
und man hat für δ = 0,01mm, Γ =
1,884; dieser Fehler in der Angabe des Zeigers entspricht aber einer Fläche von
2,355 □mm, um welche die Fläche des
Kreises zu groß oder zu klein gefunden wird, je nachdem δ positiv oder negativ ist.
In dieser Größe des Fehlers liegt aber auch das Mittel ihn zu beseitigen; denn wenn
man denselben für diesen größten Kreis, welcher ohne unterliegende Figur, also auch
ohne die mit dem Nachfahren unzertrennlichen Fehler beschrieben werden kann, indem man den Rahmen K durch die Leisten J
festklemmt, durch Correction der Stellung der Loupe so klein als möglich gemacht
hat, so wird er für kleinere Figuren, und namentlich für solche, bei welchen auch
eine Bewegung im Sinne der negativen ω
stattfindet, verschwindend klein werden.
Dieser Nachtheil meines Instrumentes, wenn man ihn nach dem Vorhergehenden noch so
nennen kann, da er nur auf eine vorzunehmende Correction zurückkommt, dürfte
indessen nach meiner Ansicht durch die Vorzüge desselben mehr als aufgewogen
werden.
Außerdem, daß die bei dem Wetli'schen Planimeter
stattfindende, den Principien der angewandten Mechanik widerstrebende Bewegung eines
Wagens mittelst eines einarmigen Hebels und der daraus folgende schon von Stampfer bemerkte Fehler beseitigt ist, und hier alle
Bewegungen in ungezwungener Weise stattfinden, halte ich auch die Beseitigung des
bei jenem Planimeter angewendeten Drahtes zur Bewegung der Scheibe für einen Vorzug,
da sich dieser Draht bei längerer Anwendung des Instrumentes dehnen und durch die
fortwährende Biegung und Streckung selbst zerreißen wird, und mit dem Einspannen
eines neuen Drahtes eine Aenderung in der Angabe des Instrumentes eintritt, wenn der
neue mit dem alten nicht vollkommen gleiche Dicke hat.
Die Angabe des Wetli'schen Planimeters kann nur dadurch
geprüft werden, daß man einer vorgezeichneten einfachen Figur nachfährt, und die
Angabe des Instrumentes mit der geometrischen Berechnung vergleicht, während bei
meinem Instrumente Kreise von verschiedenen Halbmessern beschrieben werden können,
ohne daß man mit dem Auge der Figur folgen muß, also auch ohne die von diesem
Nachfahren unzertrennlichen Fehler.
Bei jenem Instrumente kann der Werth eines Theiles auf dem Zifferblatte nur durch
Abdrehen oder Abschleifen des Rädchens U auf eine
bestimmte Fläche zurückgeführt werden; dieser Zweck kann daher nur nach vielen
Proben und nach den Versuchen von Stampfer und Bauernfeind kaum so erreicht werden, daß nicht eine
Correction nothwendig würde. Bei meinem Instrumente kann man dagegen, ohne das
Rädchen U zu ändern, durch eine kleine Verschiebung der
Achse O mittelst der Schrauben m das Verhältniß h₃/h₂, also auch den Coefficienten k und den Werth eines Theiles auf dem Zifferblatt ändern
oder corrigiren, und diese Operation kann gleichzeitig mit der Correction der
Stellung der Loupe vorgenommen werden.
Ferner dürfte auch die bei meiner Einrichtung erzielte Bequemlichkeit, daß man das
Zifferblatt direct vor sich hat und bei jeder Stellung des Instrumentes leicht
ablesen kann, nicht zu übersehen seyn.
Endlich glaube ich noch erwähnen zu müssen, daß mein Instrument sich namentlich für
die Berechnung der Mittelwerthe aus physikalischen Beobachtungen, welche durch
sogenannte Auto- oder Metrographen aufgezeichnet worden, eignen dürfte, da diese Instrumente
viel einfacher werden, wenn man jene Beobachtungen auf eine gleichförmig sich
umdrehende Scheibe aufzeichnet, als wenn man dazu einen geradlinig sich bewegenden
Papierstreifen anwendet; auf diese Scheibe kann dann mein Planimeter unmittelbar
aufgesetzt und die Fläche des Sectors berechnet werden, welcher von der
aufgezeichneten Figur und den beiden, Anfang und Ende der Beobachtungszeit
bezeichnenden Radien begränzt wird. Nennt man diese Fläche S, die Umlaufszeit der Scheibe T, die Zeit der
Beobachtung t und den gesuchten Mittelwerth h, so hat man für den der Beobachtungszeit
entsprechenden Drehungswinkel ω den Werth
ω = 2π T/t
und da der mit dem constanten Mittelwerth h beschriebene Kreissector der Sectorfläche S gleich seyn muß, die Gleichung
1/2 h²ω = πh² T/t = S,
woraus sich jener Mittelwerth in der Form
h = √(ST/πt)
ergibt.
Zum Schluß erlaube ich mir, noch auf eine Probe dieser Instrumente aufmerksam zu
machen, welche weder von Stampfer noch von Bauernfeind erwähnt wird und welche mir besonders
geeignet erscheint, über die Genauigkeit des Instrumentes Aufschluß zu geben,
namentlich in Betreff der etwa vorhandenen todten Bewegung. Diese Probe besteht
darin, daß man zuerst eine Figur ein- oder mehrmal vorwärts, im Sinne des
Zifferblattes, und dann wieder eben so oft rückwärts umfährt, wobei der Zeiger am
Ende auf den frühern Standpunkt zurückgehen müßte, wenn keine todte Bewegung
vorhanden ist, während sich im entgegengesetzten Falle die Größe derselben schon bei
einmaligem Umfahren der Figur verdoppeln wird; dadurch kann also das Vorhandenseyn
einer solchen todten Bewegung leicht erkannt und ihre Größe ermittelt werden, da
sich die Fehler ist der Führung des Index nahezu compensiren werden.
Tafeln