| Titel: | Ueber Ballistik; von L. Georg Treviranus. |
| Autor: | Ludwig Georg Treviranus [GND] |
| Fundstelle: | Band 143, Jahrgang 1857, Nr. I., S. 2 |
| Download: | XML |
I.
Ueber Ballistik; von L. Georg Treviranus.
Mit einer Abbildung auf Tab. I.
Treviranus, über Ballistik.
Unter Ballistik versteht man gewöhnlich die Wissenschaft, nach mechanischen und
physikalischen Grundsätzen genau die Form der krummen Linie zu bestimmen, welche ein
aus einem über die Horizontale erhöhten Geschütz abgeschossenes Projectil in der
Luft beschreibt, und man nennt die Aufgabe eine solche Kugelbahn zu bestimmen, sehr
passend das ballistische Problem, indem diese Aufgabe selbst bis zum heutigen Tage
noch nicht genügend gelöst ist. Doch sind hier zwei Fälle zu unterscheiden. Einmal
abstrahirt man von dem Widerstand der Luft, betrachtet die Sache so, als wenn sich
das Geschoß in einem leeren Raum bewegte und nennt die für diesen Fall entwickelte
Theorie die parabolische. Diese so schöne Theorie läßt in der That schon seit langer
Zeit wohl nichts mehr zu wünschen übrig, indem sie von allen competenten
Mathematikern als vollkommen richtig, also keiner weitern Verbesserung mehr fähig
anerkannt worden ist. Aber mit Berücksichtigung des Widerstandes der Luft ist dieses
durchaus nicht mehr der Fall. Die hierauf bezügliche Theorie nennt man zum
Unterschied von jener, die Theorie des Widerstandes, und wenn sich auch nicht
verkennen läßt, daß auch auf deren Vervollkommnung von den dazu Befähigten nicht
minder viel Zeit und Scharfsinn verwendet worden ist, so war doch, so viel man weiß,
noch keiner so glücklich, den beabsichtigten Zweck zu erreichen, und die praktische
Artillerie hat bis jetzt nur einen sehr spärlichen Nutzen aus den Resultaten der
gelehrten Untersuchungen ziehen können. Nahe dasselbe dürfte auch, wie mir scheint,
der Fall in Bezug auf die Versuche seyn, welche mittelst des sogenannten
ballistischen Pendels in England, Frankreich und Amerika angestellt wurden. In dem
Aufsatz „über die Gesetze des Widerstandes der Luft
gegen Projectile
von großer Geschwindigkeit“
Polytechn. Journal Bd. CXLI S.
275. hält der Verfasser, Hr. Didion, die zu Metz
mittelst des ballistischen Pendels angestellten Versuche unter allen für die
verläßlichsten. Dem soll hier zwar keineswegs widersprochen werden; aber was lernt
man unter anderm (in den für die praktische Artillerie besonders wichtigen Fällen,
aus der Anfangsgeschwindigkeit des Geschosses und dem Höhenwinkel des Geschützes
entweder die Kernschußweite auf der Horizontale im Niveau mit der Kugelsohle, oder
die Wurfweite aufs Bett zu bestimmen) aus dem Aufsatz? Ich selbst habe mindestens
keine Regel daraus entnehmen können, welche auf die genannten Fälle anwendbar wäre,
und ein Freund von mir, welcher als ein guter Mathematiker betrachtet wird, hat sich
auch vergebens darum bemüht. Dagegen mag richtig seyn, was man übrigens auch schon
früher vermuthete, daß der Widerstand der Luft, eine geringe Geschwindigkeit des
Geschosses als Norm angenommen, nicht nach Newton's Satz
nach den Quadraten derselben, sondern mit vergrößerter Geschwindigkeit in einer
höheren Progression zunimmt. In welchem speciellen Betrag dieses der Fall ist, soll
eine Formel lehren, welche Didion dafür gibt. Aber was
sich Nutzbares daraus wird machen lassen, scheint auch die Zukunft erst lehren zu
müssen.
Was ich mir nun erlauben werde über Ballistik in praktischer Beziehung mitzutheilen,
macht, wie ich im voraus bemerke, auf wissenschaftliche Begründung aus den
Grundsätzen der Mechanik, bezüglich der bewegenden Kraft, wohl einige, aber aus
denen der Physik, bezüglich des Luftwiderstandes, vorläufig keine Ansprüche, sondern
das Ganze beruht zur Zeit noch auf einer Hypothese, welche sich aber, wie weiterhin
gezeigt werden wird, den wirklichen Versuchen so gut anschmiegt, daß ich hoffe man
wird zu der Ueberzeugung gelangen: die wahre Theorie des Widerstandes muß,
mindestens sehr nahe, in dem von mir aufgefundenen Ausdruck enthalten seyn; so daß
Mathematiker vom Fach wahrscheinlich nur noch die Aufgabe haben werden, den näheren
Zusammenhang der Sache herauszufinden.
Die Gründe daß ich, der bis vor sechs Jahren, etwa 30 Jahre lang, Mechaniker,
hauptsächlich für den Bau der größeren, durch die Kraft des Dampfes und des Wassers
bewegten Maschinen war, nebenbei auch die Ballistik zu meinem Studium machte, liegen
einestheils in dem Umstand, daß ich in jüngeren Jahren Veranlassung dazu fand,
anderntheils daß sie mich als ein Zweig der Mechanik, eben wegen des Dunkels worin
sie gehüllt ist, ansprach, endlich darin, daß mir seitdem, etwa so wie Anderen eine Liebhaberei fürs
Scheibenschießen, die für die Ballistik geblieben ist, obgleich, was ich in dieser
Beziehung auf eigene Hand unternahm, stets nur im kleinen Maßstab geschah, während
ich Versuchen Anderer im Großen beizuwohnen nur selten Gelegenheit hatte, so daß ich
mich auch nicht rühmen kann ein praktischer Artillerist zu seyn, worauf es aber hier
auch gar nicht ankommt, indem ich nicht etwa meine eigenen, sondern die Versuche
Anderer, mir nur dem Namen nach bekannter Personen, als Norm für meine Berechnungen
annehmen werde.
Bei der Ansicht solcher Versuche, wie sie in den Schieß- und Wurftabellen der
Handbücher über das Artilleriewesen mitgetheilt sind, schwebte mir oft die Idee vor:
daß es möglich seyn möchte, durch eine oder die andere Modification der
trigonometrischen Linien des Zirkels einen Ausdruck oder eine Formel zu finden,
welche der Forderung, aus dem Elevationswinkel die Schuß- und Wurfweiten,
wenn auch nur bis zu einem gewissen Grad, mit den wirklichen Versuchen
übereinstimmend darzustellen, ein Genüge leistet. Indessen die Tabellen welche mir
bis dahin zur Hand waren, gaben alle nur die Distanzen für gewisse Höhen der
Aufsätze aufs Visir der Geschütze, und ohne ganz speciell mit deren Dimensionen
bekannt zu seyn, erschien es mir zu unsicher, die Höhenwinkel daraus zu
berechnen.
Dieß war so bis zum Jahre 1848, wo ich mit dem Werke bekannt wurde: „Versuch eines Handbuches für die königl. bayerische
Artillerie, mit 12 Steindrucktafeln
, bearbeitet von Joseph Hütz und Joseph Schmölzel (München, Druck und Verlag von Georg Franz 1847), welches ganz meinem Wunsche entsprach, da es
nicht nur die Höhe der Aufsätze, sondern auch die dazu correspondirenden Winkel der
Elevation in Graden und Minuten angibt. Ich wählte daraus die Schieß- und
Wurftafel für die leichte lange 7pfünder Haubitze mit Granaten bei 20 und 40 Loth
Ladung (S. 488) zum Vergleich mit meiner beabsichtigten Berechnung der Distanzen,
fand aber damals Schwierigkeiten eine Formel zu finden, nach welcher sich bloß aus
dem Elevationswinkel und der Erhöhung der Haubitze über dem Bett die in der Tafel
angegebenen Wurfweiten aufs Bett berechnen ließen, obgleich ich gegenwärtig die
Möglichkeit einsehe, mindestens umgekehrt aus genannter Wurfweite etc. den
Elevationswinkel zu berechnen.
Zur Aushülfe wurden also alle in dem Handbuche angegebenen Entfernungen als aus zwei
Größen bestehende Wurfweiten betrachtet, wovon die eine gleich der Kernschußweite
auf der Horizontalen im Niveau mit der Kugelsohle des Rohrs, und die andere, in
Bezug auf die Kugelbahn, eine Ordinate in der Länge gleich der Entfernung des letzten Berührungspunktes der
Granate mit der Horizontalen und dem Aufschlag aufs Bett sey.
Die parabolische Theorie lehrt, daß wenn c = der
Anfangsgeschwindigkeit des Geschosses, m = dem
Höhenwinkel des Geschützes über der Horizontalen und 2 g
= der Endgeschwindigkeit eines fallenden Körpers am Ende der ersten Secunde ist,
dann die Schußweite auf der Horizontalen wird:
b = (c² × sin 2 m)/2 g
Wird nun bei dem gleichen Geschütz und gleichbleibender Pulverladung c² als unveränderlich angenommen, so läßt sich,
da 2 g es ebenfalls ist, die Formel auch ausdrücken
durch:
b = ϐ × sin 2 m,
wo also ϐ eine Constante,
entstanden aus c² : 2g, ist.
Die Formel, welche ich aus den Versuchen ableitete, lautet:
Textabbildung Bd. 143, S. 4
und man sieht, sie ist, bis auf die Wurzel n aus sin 2 m, mit derjenigen der parabolischen Theorie
übereinstimmend.
Nur ist zu bemerken, daß, soweit meine Wissenschaft bis jetzt in der Sache reicht,
n nur aus zwei wirklichen Schießversuchen gefunden
werden kann; denn erstens muß b bekannt seyn bei m = etwa 1 1/2 bis 2 Graden, und zweitens bekannt seyn
bei, wo nicht dem höchsten, doch einem diesem nahe kommenden Winkel m, welcher bei dem Geschütze (Haubitze oder Kanone
dürfte gleich seyn, aber kein Bombenmörser) noch zulässig ist; jedoch wahrscheinlich
nicht über 18–20°. (2).
Je größer die Anfangsgeschwindigkeit des Geschosses, desto größer fällt auch n aus, ohne jedoch anscheinend 2 erreichen zu können,
während es umgekehrt = 1 wird, wenn man den Widerstand der Luft = 0 setzen kann,
weßhalb mindestens zu vermuthen ist, daß wenn man die Sache einmal klarer als jetzt
durchschaut haben wird, n sich auch aus der
Anfangsgeschwindigkeit c, oder vielmehr aus dem
Widerstandscoefficienten des Geschosses, wird ableiten lassen, wobei dann die dafür
von Didion aufgestellte FormelSeine Formel für den Widerstand lautet: W =
(0,027 (1 + 0,0023 v) v² × Q, worin v die Geschwindigkeit des Geschosses bezeichnet,
und der Meter, das Kilogramm sowie die Secunde als Einheiten angenommen
sind, der Widerstandscoefficient R = W/(Q × v). Ob dieß wohl richtig ist? Mir scheint, das
absolute Gewicht des Geschosses und dessen mechanisches Moment muß bei R mit in Anschlag kommen. Der Verf. vielleicht gute Dienste leisten könnte, und auch die bis jetzt mittelst des
ballistischen Pendels angestellten Versuche nicht mehr als nutzlos erscheinen
würden.
Wird also, um zuvörderst den Exponenten von n zu finden,
der kleinere der beiden Winkel mit m' und die dazu
gehörige Schußweite mit b', der größere der Winkel mit
m'' und die Schußweite mit b'' bezeichnet, so verhält sich:
Textabbildung Bd. 143, S. 5
Das Ganze zur nten Potenz
erhoben:
Textabbildung Bd. 143, S. 5
Textabbildung Bd. 143, S. 5
Nachdem jetzt der Exponent der Wurzel n bekannt ist,
braucht bloß noch der Betrag der Constanten vor dem Wurzelzeichen ermittelt zu
werden, um sowohl auf die als Grundzahlen angenommenen Schußweiten b' und b'' wieder zu kommen,
als auch alle dazwischenliegenden aus dem jedesmaligen Elevationswinkel berechnen zu
können; so ist mindestens meine Annahme. Die Gleichung für die Schußweite ist, wie
schon bekannt,
Textabbildung Bd. 143, S. 5
und daraus findet sich
Textabbildung Bd. 143, S. 5
Hat man jetzt n genau genug ermittelt, so ist es
einerlei, ob die Constante ϐ aus b' und m' oder aus b'' und m'' berechnet wird:
man bekommt in beiden Fällen einen gleichen Werth für ϐ, sonst nimmt man, nach Gutbefinden, das eine oder das andere der
beiden ϐ, oder auch das Mittel aus beiden.
Ist die Schußweite auf der Horizontalen gegeben und die Frage nach dem Winkel m, so findet sich
Textabbildung Bd. 143, S. 5
woraus sich mittelst der
logarithmisch-trigonometrischen Tabellen der Winkel von 2m und, durch Halbirung, der einfache Winkel m leichtWeil m sich hier auf die Horizontale bezieht;
aber m fürs Bett richtig zu finden, ist, wie
bereits angedeutet, viel schwieriger. Der Verf. finden läßt.
Es handelt sich jetzt in Bezug auf die Wurftafeln von Hütz
und Schmölzel noch darum, einen Werth für die Länge der
schon erwähnten Ordinaten zu bekommen, um nach dessen Abzug von den Wurfweiten, die
Schußweiten auf der Horizontalen darstellen zu können. Dabei ist nun vor acht
Jahren, wie schon angedeutet, minder wissenschaftlich verfahren worden, als, wie ich
jetzt einsehe, es wohl hätte der Fall seyn können. Aber die beiden Tabellen, welche
ich liefern werde, gegenwärtig nach der neuen Ansicht der Sache nochmals zu
berechnen, geht aus mehreren Gründen nicht an. Man muß sich also schon mit Dem
begnügen was ich damals berechnete, und hoffentlich wird dieß auch meiner
Beweisführung: die Schußweiten richten sich nach
Textabbildung Bd. 143, S. 6
nicht nur keinen wesentlichen Eintrag thun, sondern vorzüglich
Praktiker im Artilleriewesen mögen nebenbei daraus entnehmen, wie man diese
Ordinaten mindestens der Wahrheit nahe kommend berechnen kann.
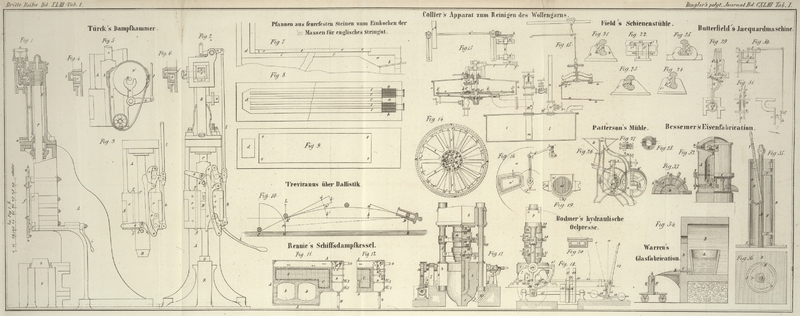
Um also in Bezug auf die Ordinate mich ganz verständlich zu machen, bedeutet in Fig. 10
CHB das Bett oder die waagerechte Sohle des
Erdreichs, über welches das Geschütz D in der Höhe BD = UK
aufgestellt ist. Die Kugel im Rohr wird dabei concentrisch mit der Schildzapfenmitte
angenommen, und wenn dieses in der Wirklichkeit auch nicht der Fall ist, so kann
doch daraus kein wahrnehmbarer Fehler entspringen. So genommen, nenne ich die
Waagerechte im Niveau mit der unteren Kante der Kugel im Rohr, die Kugelsohle oder die Horizontale, in der Figur mit KD bezeichnet, welche hier auch zugleich die
Schußweite, von der Schildzapfenmitte gerechnet, sowie CB die Wurfweite ist.
Zur Ermittelung der Länge der Ordinate CH, welche
y genannt wird, handelt es sich jetzt zunächst
darum, durch Versuche zu bestimmen, in welcher Entfernung hinter der Schießscheibe
HL die Kugel das Bett berührt, wenn die
Elevation des Geschützes so ist, daß es bei der festgesetzten Pulverladung auf der
Horizontalen den Kernschuß KD gibt. Der dazu
gehörige Höhenwinkel m scheint mir am einfachsten in der
Art gefunden werden zu können, daß man nach der beiläufigen Anfangsgeschwindigkeit
des Geschosses und der Höhe der Horizontalen über dem Bett die Distanz KD so wählt, daß, bei genau waagerechter Lage der
Seele des Rohrs, das Geschoß noch die Scheibe etwa in den Punkt p trifft, wo sich dann aus der Tiefe von p unter K und der Distanz
KD der aus der Schwerkraft des Geschosses
resultirende Depressionswinkel KDp leicht
berechnen läßt.
Macht man nun bei den folgenden Schüssen den Elevationswinkel m dem eben gefundenen Depressionswinkel gleich, so muß, wenigstens theoretisch genommen, der
Kernschuß erfolgen und man kann dann auch aus der Entfernung des Aufschlags c der Kugel von H und aus
der Höhe HK den Depressionswinkel, welchen die gerade
Linie dKc mit CH macht und
den ich m₁ nenne, berechnen. Dieser Winkel m₁ wird jederzeit größer als m befunden werden; die DifferenzDistanzm₁ – m wird β genannt, wobei, wie in der
parabolischen Theorie, der Winkel a'Kb' dem Winkel aDb = m, gleich gesetzt
wird; indem um soviel als a'Kb' in der Wirklichkeit
größer als m, dka' = β kleiner ausfällt und so die Sache sich ausgleicht.
Der Winkel β ist jetzt als eine Konstante zu
betrachten, nach welcher man, zu m hinzugefügt, wie
meine Annahme ist, CH = γ zu berechnen hat. Man schließt zu dem Ende, daß wenn HK = h genannt wird, sich verhält:
tang
m₁ : sin t = h : y
tang m₁ : sin = h : y
weßhalb für den Radius = 1
Textabbildung Bd. 143, S. 6
Die vollständige Formel für die Wurfweite wird demnach:
Textabbildung Bd. 143, S. 7
Um diese Formel auf wirkliche Fälle in Anwendung bringen zu können, muß jedoch nicht
nur der Winkel β bekannt seyn, sondern man muß
auch n und δ kennen,
welche zu finden die Gleichungen I bis V lehren, nämlich aus zwei Schußweiten b' und b'' auf der
Horizontalen und den dazu gehörigen Winkeln m' und m''. Die Schießscheibe welche ich zur Ermittelung von
β als die passendste betrachte, ist indessen
für b' und b'' nicht mehr
anwendbar, sondern ich würde, um auch in diesem Falle leicht zum Ziel zu gelangen,
das Geschütz so tief in dem Bett versenken bis die Kugelsohle im Niveau mit der
Ebene des Bettes zu liegen käme, dieses also gewissermaßen die Stelle der
Horizontalen verträte.
Ich wende mich jetzt in Bezug auf das Handbuch von Hütz
und Schmölzel zuerst zur Berechnung der Schuß- und
Wurfweiten der 7pfünder Granate bei 20 Loth Ladung der Haubitze (S. 488), und
bemerke zuvörderst, daß es mir nicht gelingen wollte eine ganz bestimmte Angabe zu
finden: wie sich die Kugelsohle des Geschützes in den Versuchen, worauf sich die
Tabelle bezieht, über dem Bette befand. Diese Höhe ist von mir = 4 Fuß, oder weil
sich die Schuß- und Wurfweiten auf Schritte von 2,4' beziehen, = 4 : 2,4 = 1
2/3 = 1,667 Schritt angenommen worden, und ich hoffe, daß darin nicht viel gefehlt
seyn wird. Der Winkel β wurde nach mehreren Berechnungen, welche ich
deßhalb anstellte, = 0° 27' gesetzt, dann nach 1,667 : tang (m + β
= m₁) die Werthe für γ gefunden, welche von den Wurfweiten D
abgezogen, die Schußweiten b gaben.
Für m' = 1° 42' fand sich b' = 357,1; für m'' = 15° 38' ist b'' = 1894,0 Schritte, und diese Daten als Grundlage zur
Berechnung von n angenommen, ergab sich als
Verhältnißzahl von b' : b''=
357,1 : 1894 = 1 : 5,304 = 1 : z.
Die Winkel verdoppelt und nach der Formel III gerechnet, ist:
log sin
31° 16'
=
0,715186 – 1
–
log sin 3° 24'
=
0,773101 – 2
––––––––––––––––––––––––––––––––
die Differenz der log
=
0,942085
––––––––––––
= n = 1,300
und
getheilt durch log
5,304
=
0,724590
Es wird also nach Formel IV die Schußweite für jeden der Winkel m
Textabbildung Bd. 143, S. 8
Damit sich nun einestheils die Division des log sin 2 m durch 1,3 verrichten läßt, und anderntheils die
Constante ϐ eine passende Größe bekommt, nehme
ich den Radius für den sin 2 m = 1000, also die Kennziffer = 3 an.
Für m' = 1° 42', 2 m'
= 3° 24' und b' = 357,1 Schritt wird nach Formel
V für ϐ
3 + log sin
3° 24' = 17,773101
–––––––––––––––––––––––––––
= 1,363924
getheilt durch n
= 1,3
welches abgezogen von log 357,1
= 2,552790
–––––––––––
ergibt die log
Differenz
= 1,188866
–––––––––––
und gibt die dazu gehörige Zahl ϐ
= 15,448.
Wird die Berechnung nach dem Winkel m'' = 15° 38'
und b'' = 1894 gemacht, so ist
3 + log sin
31° 16' =
2,715186–––––––––––––––––––––––––––getheilt
durch n = 1,3
= 2,088605
welches abgezogen von log 1894
= 3,277380
––––––––––
gibt den log
von ϐ
= 1,188775
und die dazu gehörige Zahl ϐ
= 15,445
also sehr nahe dieselbe Zahl wie oben. Es ist jedoch in der
Tabelle und der Berechnung der Werthe für b als
Constante 15,45 angenommen worden. Für 20 Loth Ladung der Haubitze ist demnach
Textabbildung Bd. 143, S. 8
nebstdem nach Formel VII, und dem darauf folgenden Text, γ =1,667 : tang (m + 0° 27') für den Radius = 1. Daß in der jetzt folgenden Tab. Nr.
1 γ dem b vorangeht,
hat seinen Grund, wie schon angedeutet wurde, in dem Gang meiner Untersuchung; in
anderen Fällen möchte es passender seyn, γ auf
b folgen zu lassen.
Betrachtet man jetzt die Tabelle Nr. 1 und vergleicht die berechneten Wurfweiten oder
Distanzen D₁ mit dem durch die Versuche
gefundenen D, so finden sich zwischen m = 0° 4' und m =
16° 46' nicht weniger als 12 Punkte, wo die Differenz im + oder – und
im Maximum nur 1/400 von D beträgt.
Bei m =1° 42', gehörend zu einer der Grundzahlen,
sollte freilich D₁ genau = 400 statt 401 seyn,
welches indessen nur andeutet, der Winkel β hätte
in Bezug auf m = 1° 42' etwas größer als
0° 27' angenommen werden sollen, wogegen er auf m
= 0° 59' und 15° 38' genau paßt, sich auch in der Mitte der Reihe bei
m = 8° 15' D₁ nur um 1/600 zu hoch, dagegen gleich darauf bei m = 9° 9' um 1/433 zu niedrig stellt, also
zwischen diesen beiden Winkeln, zwischen D und D₁, fast gar keine
Differenz sich finden würde. Kurz, die Annahmen: bei 20 Loth Ladung, der Haubitze
richtete sich b nach
Textabbildung Bd. 143, S. 9
und γ nach h : tang m₁ paßt innerhalb der angegebenen Gränze
vom Anfang bis zum Ende der Reihe. Daß bei m = 0°
4' D₁ sich um 1/20 größer als D findet, kann wohl nur seinen Grund in dem Umstand
haben, daß in dem Elevationswinkel Bruchtheile von Minuten mit aufzunehmen, den
Tabellen des Handbuches nach zu urtheilen, nicht üblich ist, und so genommen
0° 4' am besten zu der Distanz von 200 Schritte correspondirt.
Dasselbe gilt auch von Tab. Nr. 2, für 40 Loth Ladung der Haubitze, wo bei m = 0° 3' D₁
sogar um 1/42 größer als D ist. Aber bei m = 0° 29' vermindert sich das + schon bis auf
1/50; bei 0° 53' auf 1/88 und bei m = 1°
19' verwandelt es sich in – 1/85, so daß zwischen 0° 53' und 1°
19' die Differenz zwischen D und D₁ = 0 angenommen werden muß, wie sie
sich auch für 1° 49' und 15° 36' correspondirend zu den Grundzahlen
findet. Auch bei 6° 37', nahe der Mitte der Reihe, findet sich, nachdem ein +
= 1/175 vorausgegangen, ein – = 1/500 in der Berechnung, so daß auch in
diesem Fall eine wiewohl höhere Wurzel, als in Tab. Nr. 1, nämlich
Textabbildung Bd. 143, S. 9
auf b und für γ der Winkel β
= 0° 15 1/3' paßt.
In der ersten Reihe Tab. Nr. 1 sind freilich über 15° 36' hinaus die
Differenzen D – D₁, bedeutend größer als zwischen 0° 4' und 15° 38' und
die Berechnung gibt D₁ für m = 16° 51' und 18° 10' zu klein; in der 2ten Reihe Tab. Nr. 2 findet
sich indessen über 15° 36' hinaus das Gegentheil, so daß sich die Sache
einigermaßen ausgleicht, mindestens sich anscheinend vorläufig nicht ergibt, daß die
Formeln auf höhere Elevationswinkel als etwa 15 bis 16° nicht mehr anwendbar
seyen.
Wegen der Ungewißheit, in welcher ich mich, wie erwähnt, in Bezug auf die Höhe der
Kugelsohle befand, die der Tab. S. 488 des Handbuchs, namentlich den Wurfweiten zu
Grunde liegt, habe ich noch zu bemerken, daß wenn sie auch verschieden von den von
mir angenommenen 4 Fuß seyn sollte, dieß doch in meinen Berechnungen keinen andern
Unterschied machen würde, als daß, wenn ich z.B. h
größer als 4' angenommen hätte, die Ordinaten γ
länger und dagegen D –yD₁ = b kürzer ausgefallen seyn würde, deßgleichen
der Exponent der Wurzel n und die Constante ϐ sich etwas verändert hätten; so auch umgekehrt
bei h kleiner als 4 Fuß. Dieß gilt von beiden Tabellen.
In der 2ten bezieht sich wie in der 1sten der Radius des sin 2 m aus schon angegebenen Gründen wieder
auf 1000 und in der Berechnung der Werthe für b wurde
statt der beschwerlichen Division von log sin 2 m durch 1,571 gerechnet log
sin 2 m × 7/11, weil 11/7 auch = 1,571
ist. Weiter finde ich auch über Tab. Nr. 2 nichts zu bemerken, und ich wende mich
jetzt zu einem für das Geschützwesen sehr wichtigen Gegenstand.
Man wird nämlich bemerkt haben, daß ich mich bis jetzt insbesondere nur bemühte in
den beiden Tabellen aus den erfahrungsmäßigen Elevationswinkeln die dazu gehörigen
Wurfweiten darzustellen. Dieß ist, wie wohl zugegeben werden wird, zwar gelungen,
indessen umgekehrt aus den gegebenen Wurfweiten D, bei
bekannter Erhöhung der Horizontale über dem Bett, die dazugehörigen Elevationswinkel
zu berechnen, dazu findet sich bei mir noch keine Formel, jedoch in den
„Vorlesungen über Mathematik“ von Georg Freiherrn v. Vega, Bd. III S. 110 eine auf die parabolische Theorie
bezügliche, für den Fall entwickelt, wenn der Wurf von einem höheren nach einem
tiefer gelegenen Punkt erfolgt; sie lautet:
sin (2
m + u) = (b × cos
u)/a – sin u
(sin 2 m + u) = (b × cos u)/a
in welcher, wie bei mir, b die
Horizontale und a die größtmögliche Schußweite für m = 45°, ferner mit Bezug auf Fig. 10
u den Depressionswinkel DCB bedeutet. Aber in der Anwendung auf meine Berechnungen ist cos u das Hinderniß, weil sich, wie es scheint, nicht
leicht wird angeben lassen wie cos u modificirt werden
muß, um in Einklang mit meinen übrigen Formeln zu kommen und in Bezug auf m ein richtiges Resultat zu geben. Ein Werth für a ließe sich aus
Textabbildung Bd. 143, S. 10
wohl berechnen. Die Schwierigkeit der Modification der obigen
Formel fand ich auch schon vor acht Jahren, hielt es dann nicht für passend die
Sache weiter zu verfolgen, und überlasse es jetzt Anderen sich daran zu
versuchen.
Dagegen habe ich gegenwärtig eine Berechnungsart für m
aus D entdeckt, wo cos u und
der Werth von a gar nicht vorkommt, und welche, wenn sie
auch nicht als ganz theoretisch richtig anerkannt wird, doch, wie sich bei einem
halben Dutzend Berechnungen fand, nach Tab. Nr. 1 und 2 geurtheilt, die
Elevationswinkel in für die Wurfdistanzen stets bis auf einige Minuten genau gab,
und diese Berechnungen erlaube ich mir zur vorläufig möglichen Vervollständigung der
Sache noch anzuführen.
Wenn also D die Wurfdistanz festgesetzt und die Höhe h der Horizontalen über dem Bett bekannt ist, dann läßt
sich zuvörderst aus h : D
für den Radius = 1 die tang des Depressionswinkels u berechnen und daraus u
selber finden. Wird jetzt D = b als Schußweite auf der
Horizontalen angenommen, so hat es auch keine Schwierigkeit, für den Radius = 1000
nach der Formel
sin 2 m = (b : ϐ)n
den einfachen zu obigem b
gehörigen Winkel m + u = m*
zu finden, so daß man anscheinend u nur von m* abzuziehen braucht, um den Elevationswinkel für D zu bekommen. Indessen aus Gründen welche mir bis jetzt
nicht klar genug sind um sie hier angeben zu können, genügt der Abzug des einfachen
u von m* nicht, sondern
m* – un
gibt das richtigere m.
Es folgen hier einige Berechnungen des Winkels m aus D.
Nach Tab. Nr. 1
ist für m = 0° 59', D = 300; h =
1,667, n = 1,3
––––––––––––––––––––––––––––––––––
log 1,667 = 0,21194
–
log 300 =
2,47712
––––––––––––––––––––––––––––––––
log
tang u = 0,73482 – 3
der Winkel u
= 0° 18,6'
log
300 = 2,47712
– log 15,45 =
1,18893
––––––––––––––––––––––––––––––––––––––––––––
log
sin 2 m* = 1,28819 × 1,3
= 1,67465 – 3
der Winkel m* = 2°
42,6' : 2
= 1°21,3'
abgezogen der Winkel 0° 18,6' × 1,3
= 0°24,2'
––––––––––––––––––––––––––––––––––––––––––––
statt obiger
0° 59' ergibt sich m
= 0°57,1'
also zu wenig 0°1,9'.
Nach Tab. Nr. 1.
Für m = 8° 15' und D = 1200 findet sich
der
Winkel der tang
u = 0°
4,7'
Winkel sin m* = (1200 : 15,45)1,3/(2 × 1000) = 8°
19,7'
abgezogen
u × n = 0°
4,7' × 1,3 = 0° 6,1'
––––––––––––––––––––––––––
bleibt
statt 8° 15' der Winkel m =
8° 13,6'
und die Berechnung
gibt – 0° 1,4'.
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Für
m = 15° 38' und D = 1900
ist
Winkel der tang u =
0°3'
der Winkel sin m* = (1900 : 14,45)1,3/(2 ×
1000) = 15°42,1'
abgezogen u × n =
0° 3' ×
1,3 = 0° 3,9'
––––––––––––––––––––––
bleibt
statt 15° 38' der Winkel m = 15°38,2'
und
die Berechnung gibt + 0° 0,2'.
Nach Tab. Nr. 2
ist für m =
1°49', D =
700, h =
1,667 und n =
1,571
––––––––––––––––––––––––––––––––––––––––––––
log
1,667 = 0,21194
– log 700 = 2,84510
––––––––––––––––––––––––––––––––
log tang u = 0,36684 – 3
der Winkel u = 0°8'
log 700 = 2,84510
– log
46,73 = 1,66960
––––––––––––––––––––––––––––––––––––––––––––––––
log
sin 2 m* = 1,17550 × 1,571 = 1,84721
– 3
Der Winkel m* = 4°2,0' : 2
= 2° 1,0'
abgezogen
der Winkel 0° 8' × 1,571
= 0°12,6'
–––––––––––––––––––––––––––––
bleibt statt 1°49' m
= 1°48,4'
also zu wenig um 0° 0,6'.
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Für m = 6° 37' und D = 1500 findet sich
der
Winkel der tang
u = 0° 3,7'
Winkel sin m* = (1500 : 46,73)1,571/(2 × 1000) = 6° 44,0'
abgezogen u × n = 0° 3,7' ×
1,571 = 0° 5,8'
–––––––––––––––––––––––––––––––
bleibt statt 6° 37' der Winkel m = 6°
38,2'
und die Berechnung gibt dießmal + 0° 1,2'.
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Für
m = 15° 36' und D
= 2500
ist der Winkel u =
0° 2,3'
der Winkel sin m* = (2500 : 46,73)1,571/(2 × 1000) = 15° 39,9'
abgezogen
u × n = 0° 2,3' × 1,571
= 0° 3,6'
bleibt statt 15° 36' der Winkel m
= 15° 36,3'
und
die Berechnung gibt + 0° 0,3'.
Man sieht, die Art wie in diesen Beispielen aus h und D der Elevationswinkel m für
den Wurf der Granate aufs Bett berechnet wurde, paßt auf die wirklichen m gar nicht übel, und sie muß also mindestens als der
Wahrheit nahe kommend betrachtet werden, obgleich darin einiges problematisch ist;
denn wie man z.B. in der parabolischen Theorie rechnet, sollte m nicht = (2 m* : 2)
– un, sondern = (2 m* – u) : 2 seyn, was sich indessen in
den Berechnungen nicht bewährt hat.
Ob nun meine Berechnungsart für m hinreichend genau ist,
um darnach, für den praktischen Gebrauch der Artillerie, die Wurftabellen für
Granaten anfertigen zu können, müssen genauere und weitere Untersuchungen lehren, wo
nicht, so dürften doch die nach (2 m* : 2) – un für D gefundenen
m genau genug seyn um daraus, wie in den beiden
Tabellen, mit Berücksichtigung des Depressionswinkels m
+ β = m₁ die
Ordinaten γ nach h :
tang m₁ für den Radius 1 zu berechnen und
zuletzt aus D – γ, der Schußweite d auf der Horizontalen, wie in den obigen Berechnungen,
nur ohne Abzug von un,
(b : ϐ)n/(2 × 1000) = m;
und finden keine Fehlschlüsse statt, so sollte das eben
gefundene m dem aus m*
– un gefundenen gleich seyn; man bekommt
mindestens zwei Werthe für m, zum Vergleich und zur
Auswahl.
Wenn der Formel für die Ordinate γ auch eine
wissenschaftliche Begründung fehlt, so hat sie doch die Erfahrung für sich, indem
sie mindestens bei Versuchen im Kleinen, wo die Kugel durch eine stets gleiche
mechanische Kraft getrieben wurde, und obgleich das Verhältniß der Höhe von h zu D viel größer war als
es in der Regel beim wirklichen Geschütz ist, sich stets bewährt hat, wie auch in
den Tabellen.
Im Anfang dieser Abhandlung stellte ich die Vermuthung auf, daß sich im Laufe der
Zeit ein gewisses Verhältniß zwischen der Wurzel aus sin
2 m und dem Widerstandscoefficienten des Geschosses
möchte ermitteln lassen; indessen der Coefficient setzt voraus: daß man, außer dem
Durchmesser und dem absoluten Gewichte des Geschosses auch dessen
Anfangsgeschwindigkeit kennt, weßhalb es mir zur ferneren Erweiterung der Ballistik
zweckmäßig erscheint noch den Weg anzugeben, auf welchem sich mittelst meiner
modificirten Formel und einer Formel der parabolischen Theorie die
Anfangsgeschwindigkeit mindestens annähernd richtig finden läßt.
1) Wird also in Tab. Nr. 1 die auf Schritte berechnete Formel für b auf Fuß 2,4 gebracht, so wird sie
Textabbildung Bd. 143, S. 13
nimmt man ferner den Elevationswinkel m
= 0° 3' an, so ergibt sich auf der Horizontalen die Schußweite
Textabbildung Bd. 143, S. 14
d. i. beiläufig nur so groß als man bei den Versuchen mittelst
des ballistischen Pendels auch genöthigt ist von diesen mit dem Geschütz sich zu
entfernen, und berechnet man zuletzt zu der Schußweite von 56,52 Fuß und m = 0° 3' nach der parabolischen
Theorie die Anfangsgeschwindigkeit c, so findet
sich:
Textabbildung Bd. 143, S. 14
aber in der Wirklichkeit, nämlich mit Rücksicht auf den
Widerstand der Luft, jedenfalls noch etwas größer, indem wegen der Abnahme des
Widerstandes während des Fluges, die Geschwindigkeit von 1002' nur eine mittlere
genannt werden kann.
2) Wird in Tab. Nr. 2 die Formel für b ebenfalls auf Fuße
gebracht, so ergibt sich:
Textabbildung Bd. 143, S. 14
und den Elevationswinkel m wie
oben = 0° 3' angenommen, bekommt man als Schußweite
Textabbildung Bd. 143, S. 14
zuletzt die Anfangsgeschwindigkeit
Textabbildung Bd. 143, S. 14
dieß wäre bei 20 und 40 Loth Ladung im Verhältniß = 1002 :
1688 = 1 : 1,68 mehr.
3) Aber fraglich ist, wenn von dem Verhältniß des Exponenten von n zum Widerstandscoefficienten von c die Rede ist: ob man c für
gleiche Elevationswinkel oder für gleiche Schußweiten berechnen soll? denn,
berechnet man nach der ersten, auf Tab. Nr. 1 bezüglichen Formel das zu m = 0° 11,5' gehörige b nach
Textabbildung Bd. 143, S. 14
so findet sich b = 160 Fuß, also
nur um eine Kleinigkeit größer als 159,87' in der vorigen Berechnung, aber in diesem
Fall wird
Textabbildung Bd. 143, S. 14
woraus folgt, daß bei der gleichen Pulverladung von 20 Loth,
durch Vergrößerung der Schußweite von 56,52 auf 160 Fuß, die mittlere
Geschwindigkeit der
Granate umgekehrt von 1002 auf 861 Fuß per Secunde
abgenommen hätte. Dieß erscheint zwar auch mir als sehr viel; aber ich sehe dagegen
auch nicht ein, was sich Erhebliches gegen die Berechnungen könnte einwenden lassen,
es müßte denn seyn daß sich darthun ließe: die Schußweiten richten sich bei so
flachen Winkeln als bei den letzten drei Beispielen in Rechnung kamen, nicht mehr
wie bei den höheren Winkeln und im Durchschnitt genommen nach
Textabbildung Bd. 143, S. 15
sondern nach einem anderen Gesetze, etwa nach
Textabbildung Bd. 143, S. 15
oder auch nach
Textabbildung Bd. 143, S. 15
oder von 2 m, was mir auch nicht
unmöglich erscheint, jedoch erst durch wirkliche, auf die flachen Winkel bezügliche
Versuche, festgestellt werden müßte.
So lange als man übrigens über den Punkt nicht ganz im Klaren ist, wie sich aus der
Schußweite die Anfangsgeschwindigkeit in allen Fällen, nämlich für jedes Geschoß,
verläßlich ableiten läßt, wird sich auch nicht wohl ermitteln lassen: ob und welches
Verhältniß zwischen dem Exponenten von n und dem
Widerstandscoefficienten bestehen mag; indem dieser doch wohl auf keine andere als
die wirkliche Anfangsgeschwindigkeit sich beziehen kann. Hat man aber genanntes
Verhältniß einmal festgestellt, dann glaube ich dürfte sich in wissenschaftlicher
Beziehung manches Nützliche daraus folgern lassen und man in praktischer Beziehung
dadurch in den Stand gesetzt seyn, etwa bei einem neu projectirten Geschütze dessen
Schußweite im voraus mindestens annähernd richtig bestimmen zu können.
Auf Vollkugeln haben sich meine Untersuchungen freilich nicht so speciell erstreckt,
daß ich hier Mittheilungen darüber machen könnte, indessen hoffe ich doch, daß auch
bei diesen entweder
Textabbildung Bd. 143, S. 15
oder die Wurzel aus der einen oder der anderen der oben
benannten trigonometrischen Linien anwendbar seyn dürfte, nur, wie ich schon anfangs
bemerkte, nicht auf das Werfen der Bomben und über Winkel von 45°, weil man
z.B. für m = 15° und m = 75°, wie nach der parabolischen Theorie, in beiden Fällen eine
gleiche Wurfweite bekommen würde und doch nach Maßgabe als das Geschoß länger in der
Luft verweilt, es mehr von seiner anfänglichen Geschwindigkeit verlieren muß,
folglich die Wurfweite bei 75° nie so groß als bei 15° ausfallen kann,
wie auch die Erfahrung lehrt.
Tabelle Nr. 1, enthaltend eine Berechnung der Wurfweiten
der 7pfünder Granate bei 20 Loth Ladung der Haubitze, zum
Vergleich mit den wirklichen Wurfweiten nach dem Handbuche von Hütz und Schmölzel S. 488.
Textabbildung Bd. 143, S. 16
Winkel der Elevation = m;
Wurfweite, wirkliche = D; Winkel β; Wurfweite unter der Horizontalen;
Schußweite auf der Horizontalen; Wurf- u. Schußweite aufs Bett; Die
Berechnung gibt gegen D + oder –
Tabelle Nr. 2, enthaltend eine
Berechnung der Wurfweite der 7pfünder Granate bei 40 Loth
Ladung der Haubitze, zum Vergleich mit der wirklichen Wurfweite, nach dem Handbuch
von Hütz und Schmölzel S.
488.
Textabbildung Bd. 143, S. 17
Winkel der Elevation = m;
Wurfweiten, wirkliche = D; Winkel β; Wurfweite unter der Horizontalen;
Schußweite auf der Horizontalen; Wurf- und Schußweite aufs Bett; Die
Berechnung gibt gegen D + oder –
Tafeln