| Titel: | Das Zahnexcentricum, ein neuer Bewegungsmechanismus; von Prof. F. Reuleaux in Zürich. |
| Fundstelle: | Band 148, Jahrgang 1858, Nr. V., S. 16 |
| Download: | XML |
V.
Das Zahnexcentricum, ein neuer
Bewegungsmechanismus; von Prof. F.
Reuleaux in Zürich.
Aus dem Civilingenieur, 1858 Heft 1, durch das
polytechnische Centralblatt, 1858 S. 151.
Mit Abbildungen aus Tab.
I.
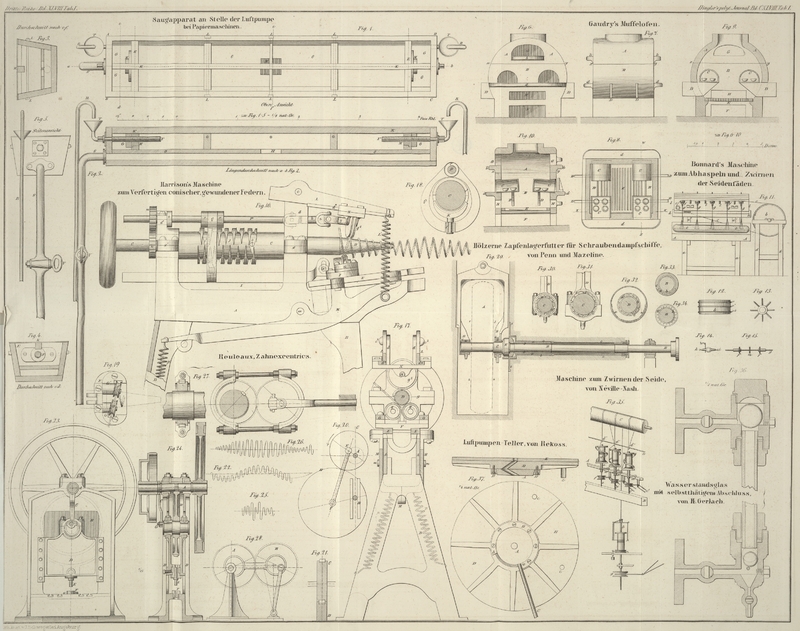
Reuleaux' Zahnexcentricum.
Mit dem Namen „Zahnexcentricum“ hat
der Verfasser einen wesentlich neu scheinenden Mechanismus belegt, welchen er durch
eine gewisse Zusammensetzung von Zahnrädern erhielt, und welcher so vieler
praktischen Verwendungen fähig ist, daß seine Veröffentlichung nützlich seyn möchte.
Es folgt deßhalb hier die Darlegung der Grundidee, der
Theorie und einiger der wichtigsten praktischen Anwendungen des neuen Mechanismus.
1. Der allgemeine Fall. Gibt man zwei runden,
cylindrischen, sich außen berührenden Scheiben von beliebiger Größe excentrische
Achsen, wovon man die eine nur drehbar, die andere aber außerdem noch in einer
geraden oder gekrümmten Bahn verschiebbar anbringt, so wird sich bei der Drehung der ersten Scheibe die Achse der zweiten verschieben, vorausgesetzt, daß die Umfänge der Scheiben
nicht auf einander gleiten, und zwar wird die Bewegung der Achse eine hin- und hergehende
seyn, wenn dafür gesorgt wird, daß die Scheibenumfänge nicht außer Berührung kommen.
Das Gesetz dieser Hin- und Herbewegung wird sich nach der Größe der Scheiben
und Excentricitäten und nach einigen anderen Verhältnissen richten, läßt sich aber eben
dadurch, wie man auf den ersten Blick sieht, auf sehr mannichfache Weise gestalten.
Die praktische Verwirklichung dieses Mechanismus ist das Zahnexcentricum.
A, Fig. 20, ist die
unverschiebbar gelagerte Achse der Scheibe C, welche auf
A excentrisch befestigt ist, B die Achse der zweiten Scheibe D, hier in
einer geraden, durch den Mittelpunkt von A gehenden Bahn
verschiebbar. Damit die Umfänge der Scheiben nicht aufeinander gleiten können, sind
die letzteren als Stirnräder hergestellt; jedoch unterscheiden sie sich von den
gewöhnlichen Zahnrädern dadurch, daß sie seitlich mit abgedrehten Rändern vom
Durchmesser ihrer Theilkreise versehen sind, s. Fig. 21. Diese Ränder
rollen beim Eingreifen der Räder aufeinander, so daß die letzteren im Stande sind,
auch radial gerichtete Pressungen aufeinander auszuüben. Es ist nun noch
erforderlich, eine Vorrichtung anzubringen, vermöge deren die Scheibenränder immer
in gegenseitiger Berührung erhalten werden. Hierzu könnte man ein die Achse B gegen A treibendes
Gegengewicht oder auch eine Feder anwenden, wie man es nicht selten bei
Kniehebelpressen oder Kurbelpressen (z.B. bei der Vorsig'schen Stanzmaschine) findet. Allein die Sache läßt sich hier in der
Regel weit einfacher machen. Da nämlich die Punkte E und
F als Mittelpunkte der Räder stets dieselbe
Entfernung einhalten müssen, so braucht man den Rädern nur außer den excentrischen
Zapfen auch noch centrische zu geben und diese durch eine Zugstange zu verbinden, wie es in Fig. 20 angedeutet
ist.
Das Ganze läßt sich, wie man noch weiter unten sehen wird, sehr leicht constructiv
ausführen, und die Vorrichtung wird dann beim Drehen des Rades C das folgende Spiel haben. Treibt man das Rad C, welches zur Unterscheidung von dem verschiebbaren oder Schubrade
D das feste Rad heißen möge,
in der Richtung des beigezeichneten Pfeiles um, so wird D in der entgegengesetzten Richtung in Drehung versetzt, und dadurch B nach unten geschoben. Wird dabei dem Punkte B ein (überwindbarer) Widerstand entgegengesetzt, so
ruft derselbe einestheils einen Druck der Scheibenränder aufeinander hervor, und
zugleich, wenn die hierbei auf den Rändern entstehende Reibung nicht zum Mitnehmen
genügt, auch noch einen Druck zwischen den Radzähnen. Durch diese Pressungen
gemeinschaftlich wird die treibende Kraft nach B
verpflanzt. Ist B am Ende seines Schubes angelangt, so
wird es durch den Zug der Stange E, F und die
umtreibende Kraft der Radzähne wieder in die Höhe bewegt, um nach Durchlaufung eines
gewissen Weges wieder nach unten getrieben zu werden.
Um zu einer allgemeinen Anschauung über das Gesetz der Bewegung des Punktes B zu gelangen, werde vorerst das Rad D lose auf seiner centrischen Achse F, und zugleich diese nur in einer zu AB parallelen Richtung verschiebbar gedacht,
alsdann wird D beim Drehen des Rades C die Stelle einer Reibungsrolle vertreten, und BF in ganz ähnlicher
Weise auf- und niedergeschoben werden, als ob die Bewegung durch eine Kurbel
vom Halbmesser AF erzeugt würde. D ist aber in der That fest auf F, und mit diesem nur drehbar um B; in Folge
dessen wird der Punkt B bei jeder ganzen Umdrehung des
Rades D auch noch eine ganze Hin- und Herbewegung
machen, welche einer solchen sehr ähnlich seyn muß, die ihm eine Kurbel vom
Halbmesser BF ertheilen würde. Es wird also die
Bewegung von B aus zwei schwingenden Bewegungen
zusammengesetzt seyn, von denen die eine, durch AF
erzeugte, ihren Schwingungsmittelpunkt fortwährend nach dem Gesetz einer zweiten,
durch BF erzeugten Schwingung ändert. Eine solche
Bewegung läßt sich etwa durch das Diagramm in Fig. 22
versinnlichen.
Einen Bewegungsmechanismus von ähnlicher Wirkung besitzt man aber bereits, und zwar
in dem, welchen Redtenbacher in seinem Werke über die
Bewegungsmechanismen den „Interferenzmechanismus“ nennt und den man wohl nach seinem
Erfinder mit dem Namen „Römer'sche Räder“ bezeichnet. Hier verschieben zwei
durch Zahnräder gekuppelte Kurbeln mittelst Schubstangen und eines Gelenkes einen
Punkt, und ertheilen diesem, ganz ähnlich wie oben besprochen wurde, gleichzeitig
zwei schwingende Bewegungen. Diese Uebereinstimmung oder Aehnlichkeit der
Wirkungsweise zwischen den beiden Mechanismen ist sehr interessant und verdient
namentlich darum bemerkt zu werden, weil das Zahnexcentricum weit mehr zur
Construction geeignet ist, als die Römer'schen Räder, und
man daher mittelst desselben die Interferenzbewegung weit häufiger wird anwenden
können als bisher.
Nachdem hierauf der Verf. den mathematischen Ausdruck für das Bewegungsgesetz der
losen Achse des Zahnexcentricums ermittelt hat, geht er auf besondere Fälle über, in
welchen das Zahnexcentricum mehr als in dieser allgemeinen Form anwendbar ist.
2. Das feste Rad sey centrisch aus seiner Achse befestigt.
Man erhält dann dieselbe Wirkung wie durch einen gewöhnlichen Kurbelmechanismus, und
hieraus ergibt sich sogleich eine ganze Reihe von Anwendungen des Zahnexcentricums,
und zwar werden diese in constructiver Beziehung darum sehr brauchbar seyn, weil bei
ihnen die Kurbelbewegung und die Uebersetzung aus dem Langsamen ins Schnelle oder
umgekehrt von einem und demselben Mechanismus hervorgebracht
werden.
Macht man das feste Rad größer als das Schubrad, welch letzteres in der Regel das
getriebene seyn wird, so entstehen bei einer Umdrehung
des treibenden Rades mehrere (R/R₁ Mal so viel) Hin- und Herbewegungen
der losen Achse. Doch möchten in dieser Form Zahnexcentricum und Kurbelmechanismus
weniger vorkommen als in der Anordnung, daß das treibende Rad kleiner ist als das
getriebene. Der Kurbelmechanismus findet in dieser Weise für Pressen mancherlei Art,
als für Lochmaschinen, Nuthstoßmaschinen, kleine Hobelmaschinen, Eisenscheren
u.s.w., vielfache Anwendung. Bei allen diesen Maschinen wird er aber durch das
Zahnexcentricum meist mit großem Vortheil ersetzt werden können, und zwar aus
folgenden Gründen:
1) fällt beim Zahnexcentricum die immer sehr kostspielige Kurbel
oder Wellenkröpfung weg, indem die Achse ein ganz einfaches Stück wird;
2) ist auch die Schubstange beseitigt, indem beim Zahnexcentricum
nur eine ganz leichte Zugstange anzubringen ist;
3) können in Folge der an den Radumfängen entstehenden Reibung
die Radzähne weit schwächer gemacht werden als beim Kurbelmechanismus, und
werden deßhalb die Räder kleiner als dort, wie der
Verf. durch eine besondere Untersuchung nachweist;
4) ist die Anlage und constructive Ausführung des
Maschinengestelles beim Zahnexcentricum weit leichter zu machen als bei der
anderen Anordnung.
Die constructive Ausführung des Zahnexcentricums von der vorliegenden Gestalt läßt
sich auf sehr mannichfaltige Weise bewerkstelligen, wovon hier einige Beispiele
folgen.
Die Fig. 23
und 24 zeigen
eine Durchstoßmaschine, bei welcher der neue Mechanismus
angewandt ist. A ist das feste, B das verschiebbare Rad, C die Zugstange,
welche die Achsen der beiden Räder verbindet. Der Schlitten D wird durch die Drehung des festen Rades A
auf- und niedergeschoben, und trägt unten den Lochstempel E, welchem eine im Gestell angebrachte Matrize F entspricht. Die Abmessungen sind so gewählt, daß der
Stempel einen Druck von 50,000 Kilogr. ausüben kann. Die Achse des festen Rades
erfährt hier einen eben so großen Druck als die des Schubrades. Um sie nicht deßhalb
sehr dick machen zu müssen, sind Zapfen und Rad gleich dick gemacht, und der so
entstehende Cylinder von einer seine ganze Länge fassenden Oberschale bedeckt,
welche durch einen starken (schmiedeisernen) Lagerdeckel mit vier kräftigen
Deckelschrauben niedergehalten wird. Um die äußere cylindrische Form anwenden zu können, und
überhaupt die Anfertigung der Räder einfach zu halten, sind dieselben nach der Geradflankenverzahnung verzahnt. Die Zähne des Rades A werden hier dadurch gebildet, daß in die glatte
cylindrische Achse Vertiefungen mit radialen Flanken eingearbeitet werden, was ganz
leicht geschehen kann, überhaupt auch für kleine schmiedeiserne Getriebe zu
empfehlen ist. Man muß beim Verzeichnen der Verzahnung nur darauf achten, daß die
Eingriffdauer der Räder nicht kleiner als eine Theilung ausfällt, dieß ist durch gute Wahl der
Zahnabmessungen leicht zu erreichen, wenn die Zähnezahl nicht gar zu klein (nicht
unter 6) ist. Der excentrische Zapfen G des Schubrades
ist hier als aus einem Stück mit der Achse bestehend angenommen. Man sieht, daß das
Gestell der Maschine sich sehr günstig anordnet, und das Ganze für die Ausführung
keine Schwierigkeiten bietet, indem keinerlei schwierige Guß- oder
Schmiedestücke vorkommen.
Manchmal wird es für die Construction bequem seyn, die Ebene des Schubrades nicht
parallel, sondern senkrecht zu den Schlittenführungen
anzuordnen. Man erhält dann einen schmälern Schlitten, und kann das Gestell dann
auch gut so einrichten, daß der Tisch zugänglicher wird als hier, was z.B. für
Nuthstoßmaschinen nöthig ist. Auch bei liegendem Schlitten, den man nach Art eines
Drehbanksupports führt (z.B. bei Nietpressen), würde eine solche Anordnung
zweckmäßig seyn.
Hier und da möchte es auch von Vortheil seyn, das Schubrad B
zweischildig zu machen; der Schlitten brauchte dann nicht
gabelförmig gemacht zu werden, und man könnte die Schilde und die Achse als Ein
Gußstück herstellen; es müßte dabei übrigens sehr sorgfältig beim Abdrehen der
cylindrischen Theile des Schubrades verfahren werden, um die beiden Cylinderachsen
parallel zu erhalten.
Zu einer nützlichen Anwendung des Mechanismus leitet auch dessen Eigenthümlichkeit,
daß bei passend gemachten Verhältnissen die Zahnkraft unter allen Umständen gleich
Null (oder negativ) ausfällt, wo also die Reibung der Radränder zur Kraftübertragung
genügt, und man demnach die Zähne ganz weglassen kann. Die beiden Räder erhalten
dann glatte cylindrische Umfänge. Bringt man an einer so construirten Maschine eine
Vorrichtung an, mittelst deren man die Zugstange leicht ein wenig verlängern oder
verkürzen kann, so erhält man darin eine sehr einfache Abstellvorrichtung der Maschine. Es wären, beiläufig bemerkt, hierbei
statt einer einzigen zwei symmetrisch wirkende Zugstangen anzubringen, damit kein
einseitiger Druck stattfinden könnte: man kann dann z.B. daran die die feste Achse
fassenden Augen etwas länglich machen und einen Hebel oder eine Schraube anbringen, mittelst deren
man die Zugstangen nach der festen Achse hin ziehen könnte. Es würde dann ein ganz
leises Gegeneinanderpressen der Räder genügen, die Bewegung augenblicklich
einzuleiten, während man ebenfalls durch eine ganz geringe Verschiebung, von 1 bis 2
Millimeter etwa, die Radränder wieder außer Berührung bringen, also die
Bewegungsübertragung wieder aufheben könnte. Bedarf die Behauptung, daß die
Randreibung die Bewegung trotz dem heftigsten Widerstand zu übertragen vermag, noch
eines Beleges, so braucht man sich nur der Presse mit
Evolventensegmenten zu erinnern; bei dieser zeigt sich, daß die Reibung an
den Segmentumfängen bei gut gewählten Abmessungen niemals ein Gleiten entstehen
läßt.Eine andere interessante Folgerung des Obigen möge noch an dieser Stelle
Platz finden, und zwar eine Bemerkung über die
Anwendung der Reibungsräder überhaupt. Man kann diese nämlich, wie
das oben Gesagte bewies, sehr häufig so bauen, daß sie ganz so sicher wirken
wie Zahnräder, d.h. daß gar kein Gleiten der Umfänge
eintreten kann, selbst wenn diese eingeölt seyn sollten. Man
braucht zu diesem Ende das große Reibungsrad auf jeder Welle nur stets 10
bis 12mal (bei trocknen Umfängen nur 5 bis 6mal) so groß zu machen, als das
auf derselben Achse sitzende kleinere Rad (Reibungsrad, Zahnrad), durch
welches die Kraft in die Welle eingeleitet wird, muß aber zugleich das
nächstangreifende Reibungsrad so anordnen, daß es von
dem aus der Umfangskraft des vorhergehenden Räderpaares entstehenden
Achsendruck stets getroffen wird. Dann entsteht nämlich in jedem
Falle eine genügende Reibung, und zwar regulirt die Maschine den dazu
nöthigen Umfangsdruck selbstthätig, und genau nach Bedürfniß. Auf diese
Weise könnte man z.B. sogar die gewöhnliche
Wagenwinde ganz mit Reibungsrädern ausführen (das Zahnstangengetriebe
ausgenommen), und kann überhaupt bei Windwerken mancherlei Art die Zahnräder
durch Reibungsräder ersetzen; auch bei manchen Umtriebsmaschinen würde dieß
angehen. Bei vorhergehendem Riemenbetrieb würde sich das
Halbmesserverhältniß noch weit günstiger, etwa 3 bis 3 1/2mal kleiner als
oben herausstellen, indem dort der Achsendruck von selbst schon so viel
größer ausfällt; dieß wäre z.B. bei Uebersetzungen ins Schnelle anzuwenden.
Auch bei den sogenannten Keilrädern würde ein
weit kleineres Halbmesserverhältniß ausreichen. Auf solche Weise zur
Anwendung gebracht, können die bisher so wenig nutzbar gemachten
Reibungsräder (von den Locomotiv-Triebrädern abzusehen) oft
treffliche Dienste leisten.
Es ist klar, daß sich das Zahnexcentricum nicht nur statt des Kurbelmechanismus,
sondern auch an der Stelle anderer Kraftmechanismen gebrauchen läßt, z.B. statt des
Hebels mit Hebedaumen bei manchen Eisenscheren und Quetschwerken, statt des
Kniehebels u.s.w. So würden sich unter andern die Münzprägewerke, bei denen man sich
des Kniehebels bedient, und die dadurch nicht wenig unbehülflich und schwerfällig
werden, bei Anwendung des Zahnexcentricums sehr einfach und constructiv gestalten.
Hierbei ist noch zu bemerken, daß die Zugstange, welche beim Zahnexcentricum die
Mittelpunkte verbindet und dabei so gute Dienste leistet, sich auch beim
Kniehebel und ähnlichen Mechanismen nützlich verwenden läßt.
3. Die Räder seyen ungleich groß, aber gleich excentrisch.
Das Bewegungsgesetz der losen Achse nimmt dabei insofern eine interessante Gestalt
an, als die zu Anfang erwähnten Verschiebungen des Schwingungsmittelpunktes nun eben so groß ausfallen, als die Schwingungen, welche das
feste Rad erzeugt. Es entstehen dadurch periodische
Veränderungen in der Größe des wirklichen Hubes der losen Achse, und zwar
so, daß deren Schwingungen einen sehr wenig veränderlichen Mittelpunkt haben. Das
Bewegungsgesetz stimmt hierbei mit dem physikalischen Gesetz der Interferenzen
überein. Das die Bewegung versinnlichende Diagramm fällt je nach dem Verhältniß R/R₁ verschieden aus und kann z.B. eine Gestalt
wie Fig. 25
annehmen, wo große Hübe mit kleinen in eigenthümlicher Weise abwechseln. Das Gesagte
gilt fast wörtlich auch von den Römer'schen Rädern, wenn
man denselben gleiche Kurbeln bei ungleichen Zahnrädern gibt, und es werden solche
Mechanismen nicht selten praktisch angewandt. So z.B. findet man sie bei einzelnen
Spinnereimaschinen als Fadenführer, indem die
fortwährende Hubänderung benutzt wird, den aufzuwindenden Faden zweckentsprechend an
der Spule hin- und herzuführen; auch findet man solche Römer'sche Räder bei einzelnen Tuchdruckmaschinen dazu benutzt, die Farbewalzen und Kissen in bestimmter
Weise zu bewegen. Macht man die Räder sehr wenig verschieden, so gehen die
Hubänderungen der losen Achse sehr gleichförmig vor sich, und es entsteht eine
Bewegung, deren Gesetz sich etwa durch das Diagramm in Fig. 26 darstellen läßt.
In dieser Anordnung hat Spiller die Römer'schen Räder zur Bewegung der Pumpen solcher hydraulischen Pressen benutzt, deren Widerstand nach und nach steigt. Spiller läßt die Pumpen beim Beginn der Pressung mit
großem Hub arbeiten; der Mechanismus vermindert aber dann nach und nach den
Pumpenhub, und somit auch die zugeführte Wassermenge, bis beinahe auf Null. Zu den
angeführten und ähnlichen Zwecken kann man das Zahnexcentricum sehr gut benutzen;
doch braucht wohl nicht auf nähere Erläuterungen eingegangen zu werden.
Der einzige Punkt ist die Dauer der Perioden, innerhalb deren sämmtliche
Hubänderungen durchlaufen werden. Eine Hubperiode wird durchlaufen seyn, sobald die
beiden Räder gleichzeitig wieder ihre anfängliche Stellung eingenommen haben; die
Frage führt sich daher auf eine bei den Zahnrädern vorkommende zurück, und man
erhält für die gesuchte Periodendauer das folgende Gesetz: Die
einer Hubperiode entsprechende Umdrehungszahl des treibenden Rades ist die dem
getriebenen Rade zukommende von den beiden relativen Primzahlen, welche das
Zähnezahlverhältniß der Räder ausdrücken. (Dieser Satz gilt für die Römer'schen Räder eben so wohl als für das
Zahnexcentricum.) Verhält sich z.B. das treibende Rad zum getriebenen wie 5 : 6, so
ist die Hubperiode 6 Umdrehungen des kleineren Rades lang; hat das eine Rad 50, das
andere Rad 51 Zähne, so gehen auf die Hubperiode 51 Umdrehungen des kleineren Rades;
hat das eine Rad 18, das andere 20 Zähne, so ist die Hubperiode 9 Umdrehungen des
20zähnigen, oder 10 Drehungen des 18zähnigen Rades lang.
Die constructive Ausführung des Zahnexcentricums der vorliegenden Form läßt sich ganz
ähnlich derjenigen der folgenden Abänderung ausführen, weßhalb dieselbe hier
unbesprochen bleiben kann.
4. Die Räder seyen gleich groß und gleich excentrisch. Die
Vorrichtung in dieser letzten Form, welche der Verf. im Gegensatz zu den bisher
besprochenen, wo die Räder stets unsymmetrisch waren, als symmetrisches Zahnexcentricum bezeichnet, hat mehrere Eigenthümlichkeiten,
welche sie zu mannichfaltigen Anwendungen fähig macht, von denen im Folgenden einige
angegeben werden sollen.
Anwendung auf die Dampfschieber. Die Bewegung nach dem
Sinusverhältniß ist für die Dampfschieber so zu sagen die angemessenste, und sucht
man dieselbe durch das Excentricum mit langer Schubstange zu verwirklichen. Der von
der Schubstange herrührende Fehler ist auch in der Regel klein genug, um ganz
unberücksichtigt bleiben zu können. Doch kommt es nicht selten vor, daß für eine
genügend lange Schubstange nicht Raum ist, und hier könnte man sich dann sehr gut
des symmetrischen Zahnexcentricums bedienen, indem dasselbe ja eine sehr geringe
Längenausdehnung hat. Die constructive Ausführung kann dabei so gemacht werden wie
es Fig. 27
zeigt. Hier ist die Zugstange als ein die beiden Räder umfassender Zaum construirt,
bei welchem die Abnutzung durch Nachstellen der beiden Schrauben leicht ausgeglichen
werden kann. Dieser Zaum hat beim Zurückgehen den ganzen Zug auszuüben, während beim
Vorwärtsgehen die Radränder aufeinander drücken und die Verschiebung
bewerkstelligen. Die Excentricität der beiden Räder wäre, da der ganze Hub der losen
Achse = 4r ist, gleich dem vierten
Theil des Schieberhubes, also halb so groß als bei dem gewöhnlichen
Excentricum zu machen, sie fallen also auch kleiner als dieses aus. Der
Voreilwinkel, mit dem man sonst das Excentricum auf der Kurbelwelle befestigt, würde
auch hier beim Anbringen des festen Rades auf der Kurbelwelle
anzuwenden seyn, während hingegen das Zahnexcentricum selbst ohne Voreilen
einzurichten wäre. Auch kann man mit dem Zahnexcentricum unmittelbar eine
Schieberstange bewegen, deren Schubrichtung nicht durch die
Kurbelwelle geht, wo man also beim gewöhnlichen Excentricum Zwischenhebel
anbringen müßte.
Es entsteht hier gewiß sogleich die Frage, ob man nicht das Zahnexcentricum zur
Construction der Coulissen- oder Taschensteuerungen anwenden, und damit die für den
Locomotivenbau oft so wichtige Aufgabe lösen könne, eine gute Coulissensteuerung mit
sehr kurzen Excentricumstangen herzustellen. Diese Frage ist mit Ja zu beantworten.
Es lassen sich mit dem Zahnexcentricum mehrere Arten von Coulissensteuerungen
bilden, und zwar läßt sich z.B. die Sache so einrichten, daß
bei Anwendung nur eines Zahnexcentricums sich eine Coulissensteuerung ohne jeden
Fehler in der Schieberbewegung ergibt, für welche also das bekannte Zeuner'sche Diagramm, und zwar ein solches für constantes
Voreilen, in aller Strenge richtig ist. Bei anderen
Anordnungen entstehen trotz der kurzen Stangen keine größeren Fehler als bisher bei
Anwendung von langen Excentricumstangen.
Anwendung für Zwecke der Spinnerei Maschinen. In den
Maschinen, welche die Spinnerei anwendet, kommt manchmal die Forderung vor, einer
Welle eine hin- und hergehende und zugleich eine drehende Bewegung zu
ertheilen; man bedient sich hierzu des sogenannten Kniees. Für dieselben Zwecke
eignet sich das Zahnexcentricum sehr gut. Es wäre etwa wie in Fig. 28 anzuordnen. Hier
sind die Zapfen für die Zugstange so dick gemacht, daß sie excentrische Achsen der
Räder einschließen. Da die Kräfte zum Verschieben nicht groß sind, so können in dem
vorliegenden Falle die Radränder ganz wegbleiben, so daß also die Räder A und B gewöhnliche
Stirnräder werden. Bei einer gleichförmigen Drehung der Welle von A erhält auch B eine
gleichförmige Drehung (von dem durch die Schwingstütze hineingebrachten kleinen
Fehler abzusehen), während ihr zugleich durch die excentrischen Räder die verlangte
Hin- und Herbewegung ertheilt wird. Die Verstellbarkeit des Hubes von B durch Aenderung des Zahneingriffes könnte hier
manchmal nützlich seyn.
5. Andere Verwirklichungen der Grundidee des Zahnexcentricums.
Mehrfaches Zahnexcentricum. Man kann, wie schon oben bei dem
Spinnereimechanismus angedeutet wurde, das Zahnexcentricum auch so verwirklichen,
daß man die Radränder wegläßt und dafür das bisher als Zugstange bezeichnete Stück so stark ausführt, daß es den ganzen
Achsendruck übertragen kann. Es würde dann genau die Stelle der Schubstange des Kurbelmechanismus
vertreten. Allein mit dieser Aenderung würde nichts gewonnen, sondern nur verloren
werden, indem nun die Zähne wieder den ganzen, nicht durch die Randreibung
verminderten Umfangsdruck erführen, die Räder also wieder so groß gemacht werden
müßten wie früher. Zugleich würde dann auch die Schubstange in der Regel doppelt
angebracht werden müssen, um keine einseitigen Pressungen auftreten zu lassen.
Hierdurch würde aber der Mechanismus seiner constructiven Einfachheit, die ihn so
auszeichnet, beraubt.
Eine andere Verwirklichung des Zahnexcentricums, welche in die allgemeine Reihe
seiner Abänderungen gehört, ist die, bei welcher das eine Rad ein Hohlrad (innen verzahntes Rad) ist. Hiebei ergeben sich
ähnliche Wirkungen, wie bei den oben betrachteten Arten. Dem symmetrischen
Zahnexcentricum unter 4 entspricht in den Bewegungserscheinungen dasjenige, bei welchem das Hohlrad doppelt so groß ist als das
andere. Es wiederholen sich hier, unter der Beschränkung, daß r₁ = R₁
gemacht werden muß, die eigenthümlichen, oben gefundenen Bewegungen, wie dieß auch
aus der Theorie der Cycloiden bekannt ist. Die Anwendbarkeit des Hohlexcentricums
ist übrigens jedenfalls weit geringer als die des oben besprochenen; die
theoretische Vollständigkeit erforderte aber hier seine Erwähnung.
Endlich ist noch anzuführen, daß man durch Vereinigung von drei oder mehr Rädern in
einem Zahnexcentricum noch weitere Mechanismen bilden, auch durch Verbindung zweier
oder mehrerer vollständiger Zahnexcentrics noch zahlreiche Abänderungen des einem
Mechanismus schaffen kann, wie man es z.B. auch bei den Römer'schen Rädern gethan hat.
Tafeln