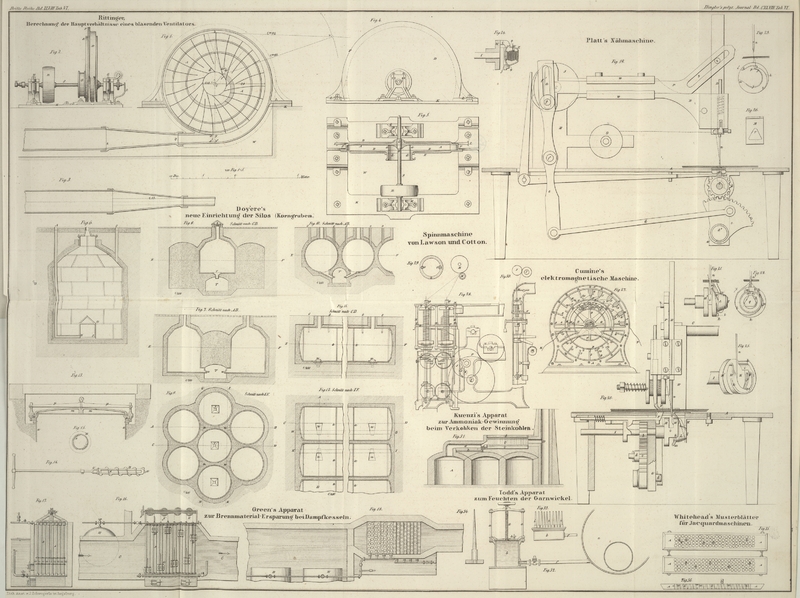
| Titel: | Berechnung und Construction eines blasenden Ventilators nach P. Rittinger. |
| Fundstelle: | Band 148, Jahrgang 1858, Nr. LXX., S. 323 |
| Download: | XML |
LXX.
Berechnung und Construction eines blasenden
Ventilators nach P. Rittinger.
Aus dem polytechnischen Centralblatt, 1858 S.
497.
Mit Abbildungen auf Tab.
VI.
Rittinger's Berechnung und Construction eines blasenden
Ventilators.
Das kürzlich bei Carl Gerold's Sohn in Wien erschienene
Werk: „Centrifugalventilatoren und Centrifugalpumpen, von P. Rittinger“, verfolgt den Zweck, eine
streng wissenschaftliche Anleitung zur Berechnung und Construction der
Centrifugalventilatoren zu liefern, und löst seine Aufgabe in sehr befriedigender
Weise. Das Buch zerfällt in zwei Abtheilungen, und enthält in der ersten die Theorie
der Gebläse überhaupt und in der zweiten die Theorie der Centrifugalventilatoren im
Speciellen. In dieser letzten Abtheilung sind zugleich die Resultate einer großen
Menge Versuche aufgeführt, die der Verf. mit genau nach seiner Theorie ausgeführten
Ventilatoren erlangt hat. Dadurch sind die Coefficienten geliefert, welche zur
Berücksichtigung der Widerstände in die Rechnung eingeführt werden müssen.
Schließlich ist die aufgestellte Theorie auf die verwandten Centrifugalpumpen
angewendet, und zuletzt in einem Anhange die Literatur der Centrifugalventilatoren
zusammengestellt. Als ein Beispiel der Behandlungsweise heben wir aus diesem Werke
hier die specielle Berechnung der Hauptverhältnisse eines blasenden Ventilators
heraus, welche auf S. 217 u. f. enthalten ist.
Der zu construirende Ventilator soll die Bestimmung haben, hochgepreßten Wind zu
erzeugen, wie solcher zum Betrieb eines Eisenhohofens gefordert wird. Um sogleich
die schwierigsten Verhältnisse zu Grunde zu legen, wird die Aufgabe dahin gestellt,
einen Hochdruckventilator zu entwerfen, welcher
M = 1 Kubikmeter = 31,7 Kubikfuß Luft in einer Secunde
mit einer Pressung von
H₄ = 0,m8 = 30,4 Zoll (Wiener)
effectiver Wassermanometerhöhe zu liefern im Stande ist; ein
Fall, wie solcher bei einem Eisenhohofen von größten Dimensionen vorkommt, welcher
mit harter Holzkohle betrieben werden soll. Nimmt man an, daß die Windmenge M = 1m in einer
Secunde bei der obigen effectiven Manometerhöhe H₄ = 0,m8 durch zwei Düsen in
den Hohofen hineingeblasen werden soll, so muß jede derselben einen Durchmesser
(1) Textabbildung Bd. 148, S. 324
erhalten, wo Mm, die Windmenge für eine Düse und eine
Minute, also Mm =
60/2 = 30 Kubikmeter zu setzen ist; es ergibt sich also:
Textabbildung Bd. 148, S. 324
Mit Rücksicht auf die Länge L der Windleitung und auf den
Durchmesser D derselben läßt sich aus H₄ die effektive Manometerhöhe H₃ berechnen, welche der Wind im Blaseraume
besitzen muß. Diese Höhe muß überdieß der Zahl und Beschaffenheit der Biegungen und
Brechungen der Windleitung angemessen vergrößert werden. Der Wahl des Durchmessers
D der Windleitung legt man die Voraussetzung zu
Grunde, daß die Luft mit einer Geschwindigkeit von 10 Metern sich darin bewege; der
gedachte Durchmesser ergibt sich dann aus
10 D²π = M,
(2) D =
√(M/10π) =
0,178√M
Da H₄ = 0,m8 ohnedieß sehr hoch angenommen wurde, so soll hier von der Röhrenreibung
abgesehen, und daher die effective Manometerhöhe im Blaseraume H₃ jener vor den Düsenmündungen gleich, also
H₃ = H₄
gesetzt werden.
Nimmt man endlich an, daß die Luft im Blaseraume mit der für die Windleitung
gewählten Geschwindigkeit sich bewege, daß also
(3) U₃ = 10m
ist, so hat man es im vorliegenden Falle mit nachstehenden
gegebenen Größen zu thun:
H = 0
U = 0
weil unmittelbar aus der atmosphärischen
Luftgesaugt wird,
H₃
= 0,m8,
U₃
= 10m,
M
= 1 Kubikmeter.
Den Halbmesser R₀ der Saugöffnung findet man unter
der Voraussetzung, daß auch im Einlauf die Geschwindigkeit
U₀ = 10m
betragen solle,
(4) R₀ = 0,18 √M =
0,m18.
Der innere Flügelhalbmesser ist
(5) R₁ = R₀.
Der äußere Flügelhalbmesser R₂ in Verbindung mit
der Zahl n der Umgänge des Flügelrades in einer Minute
ergibt sich aus
n = 845/R₂
√(H₃ – H)
Wegen H = 0 hat man
(6) n = 845/R₂ √H₃ = 845/R₂
√0,8 = 755/R₂
Man findet für
R₂ = 0,m4
den Werth von
n = 1887,
R₂ = 0,m5
„
„ „
n = 1510,
R₂ = 0,m6
„
„ „
n = 1258,
R₂ = 0,m7
„
„ „
n = 1079,
R₂ = 0,m8
„
„ „
n = 944,
R₂ = 0,m9
„
„ „
n = 839,
R₂ = 1,m0
„
„ „
n = 755,
Um eine zu große Zahl der Umgänge zu vermeiden, die stets nachtheilig auf die Dauer
und den Effect des Ventilators einwirkt, und um zugleich eine möglichst große Länge
R₂ – R₁ des Flügelraumes zu erzielen, wird man im vorliegenden Falle die
Combination
R₂ = 0,m8 und n = 944
mit Vortheil wählen.
Für den inneren Flügelwinkel α₁ hat man
(7) tg
α₁ = 0,1047nR₁/U₀ = 0,01047 nR₁
= 0,01047 . 944 . 0,18 = 1,794, α₁ = 60°50'.
Der Kreisbogen, nach welchem die Flügel gekrümmt werden müssen, um überdieß an der
äußeren Peripherie radial zu verlaufen, erhält den Halbmesser
(8) Textabbildung Bd. 148, S. 325
Die Breite des Ventilators ergibt sich zu
(9) B = 1/2 R₀ = 1/2 .
0,18 = 0,m9,
und die Höhe des Blasehalses aus
(10) Textabbildung Bd. 148, S. 325
oder, weil (R₀/R₂)² U₀² gegen das zweite Glied unter dem Wurzelzeichen
vernachlässigt werden kann,
(11) Textabbildung Bd. 148, S. 326
Für den Querschnitt A₃ der äußeren Mündung des
Blasehalses hat man die Gleichung
A₃ = M/U₃
Macht man diese Mündung rechteckig, und gibt ihr eine Breite B gleich jener des Ventilators, bezeichnet ferner ihre Höhe mit J₃, so folgt
J₃B = A₃ = M/U₃,
(12)
J₃ = m/BU₃ = M/(1/2R₀U₃) = 2M/R₀U₃.
Für die vorliegende Aufgabe würde man erhalten:
J₃ = 2/(0,18 . 10) = 1,m11.
Da jedoch die Dimensionen
B = 0,m09 und
J₃ = 1,m11
für die äußere Mündung des Blasehalses unpassend wären, so
wird man besser thun, dieser Mündung die quadratische
Form zugeben, und daher
J₃² = A₃ = M/U₃
zu setzen; daraus findet man die Quadratseite
(13) J₃ = √(M/U₃) = 0,m316.
Diese quadratische Form der Auslaufmündung hat den Vortheil, daß durch dieselbe der
Anschluß an einen gemauerten Canal, wie solcher in vielen Fällen zur Windleitung mit
Vortheil sich anwenden läßt, sehr erleichtert wird.
Sollte aber die äußere Mündung des Blasehalses wegen Anschluß an eine cylindrische
Röhrenleitung die Kreisform erhalten, so hätte man
R₃²π =
M/U₃
(14) R₃ =
√(M/U₃π) = √(M/10π) = 0,178√M =
0,m178.
Ueber die zweckmäßigste Länge des Blasehalses mangeln
verläßliche Daten; im Allgemeinen wird man den Anforderungen eines allmählichen
Ueberganges um so besser entsprechen, je länger man den Blasehals hält.
Die Zahl der Flügel wird
(15)
n = 30R₂ = 30 .
0,8 = 24.
Endlich hat man für den theoretischen Nutzeffect die Gleichung
(16)
E = MH₃γ,
weil der Voraussetzung zufolge H =
0 ist; es ergibt sich daher
E = 1 . 0,8 . 1000 = 800 Kilogrammmeter,
E = 800/75 = 10,7 Pferdekräfte.
Man sieht schon aus diesen Berechnungsresultaten, daß die Constructionsverhältnisse
eines Hochdruckventilators keine besonderen Schwierigkeiten für die Ausführung
darbieten können, indem weder die Zahl der Umgänge (n =
944), noch der äußere Flügelhalbmesser R₂ = 0,m8 eine übermäßige Größe annehmen.
Eine hohe Pressung läßt sich mittelst Ventilatoren auch
dadurch erzielen, daß man zwei Ventilatoren in der Art mit einander verbindet, daß
der zweite die vom ersten herausgeblasene und bereits verdichtete Luft aufnimmt, und
weiter auf einen höheren Grad der Pressung bringt. Da der zweite Ventilator eine
gleiche Windmenge wie der erste in Bewegung zu setzen hat, so folgt, daß alle
Dimensionen desselben, welche von der Windmenge abhängen, mit jenen des ersten
Ventilators übereinstimmen müssen; dieß gilt namentlich von R₀, R₁ und B vermöge (4), (5) und (9).
Nimmt man ferner an, daß durch jeden der beiden Ventilatoren die Steigerung der
verlangten effectiven Manometerhöhe H₃ = 0,m8 im gleichen Grade bewirkt werden solle,
so daß im Blaseraume des ersten und beziehungsweise im Saugraume des zweiten
Ventilators die effective Manometerhöhe = 1/2 H₃
= 0,m4 ausfällt, so ist die den Werth von
n und R₂
bestimmende Differenz H₃ – H
für den ersten Ventilator
1/2 H₃ – 0 = 1/2 H₃ = 0,m4,
für den zweiten aber
H₃ – 1/2H =
1/2 H₃ = 0,m4,
also für beide gleich groß; hieraus geht hervor, daß diese
beiden Ventilatoren einen gleichen Durchmesser und eine gleiche Zahl der Umgänge
erhalten, und überhaupt durchaus gleich construirt seyn müssen.
Wollte man jeden dieser beiden Ventilatoren mit dem ursprünglich berechneten Einen
gleich schnell umlaufen lassen, so folgt aus (6), wenn man dort 1/2 H₃ statt H₃
substituirt:
R₂ = 845/n
√(1/2 H₃) = 0,71 . 845/n √H₃.
Es wird daher der Halbmesser der beiden gleichen Ventilatoren 71 Proc. von jenem
Halbmesser betragen, welcher für den Einen Ventilator gefunden wurde.
Bei dem Umstande, daß die höhere Pressung sich eben so gut durch einen einzigen Ventilator erreichen läßt, wenn man demselben
einen etwas größeren Durchmesser gibt, bedarf es keiner weiteren Begründung, daß ein
Doppelventilator einem einfachen Hochdruckventilator
in praktischer Beziehung nachstehe, weßhalb auch darauf hier nicht weiter
eingegangen werden soll.
Die geometrische Verzeichnung dieses Ventilators beginnt
am einfachsten mit dem Flügelrade in der Seitenansicht
(Fig. 1
auf Tab. VI), um welches herum man sodann den spiralförmigen Theil des Auslaufes
etc. construirt.
Zu diesem Ende beschreibt man aus c mit den
Halbmessern
cb = R₂ =0,m8 und cd = R₁ = 0,m18
zwei Kreise, durch welche der Flügelraum begränzt wird, und
errichtet auf dem Durchmesser cb eine Senkrechte bz, auf welche man den unter (8) gefundenen
Krümmungshalbmesser bz = ρ = 1,m92 aufträgt.
Der mit b
z aus z beschriebene
Kreisbogen stellt die radial auslaufende Flügelcurve dar, bei welcher die Luft in
den Flügelraum ohne Stoß eintritt. Die übrigen Flügelcurven lassen sich leicht
verzeichnen, wenn man aus c mit cz einen Kreis beschreibt, und dessen Peripherie von z angefangen in n = 24
gleiche Theile theilt. Die erhaltenen Theilpunkte sind sodann die Mittelpunkte der
Flügelbögen.
Um den spiralförmigen Auslauf zu verzeichnen, macht
man
xy = i = 0,159 J₂ = 0,159 . 0,14 = 0,m022,
und zieht durch den so erhaltenen Anfangspunkt x der Spirale den Halbmesser cx, auf dessen Verlängerung man sogleich xx₁ = J₂ = 0,m14 aufträgt, weil hier die Spirale ein
schwaches Ansteigen hat.
Nun kann zur Construction der Spirale geschritten werden. Zu diesem Zwecke wurde xx₁ in 12 gleiche Theile getheilt, und auf die
Verlängerung der betreffenden 12 Halbmesser die entsprechende Zahl dieser Theile
radial aufgetragen. Der leichteren Ausführung wegen setzt hier der Auslaufraum in
gleicher Weite sich bis q fort, wodurch ein Auslaufhals gebildet wird, an welchen sich sofort der
Blasehals
qt anschließt. Die Länge
qt wurde in der Art gewählt, daß das größte Ansteigen
der geneigten Seitenwände, wie solches im Grundrisse Fig. 3 vorkommt, 1/10 der
Länge beträgt. Da nun vermöge (13) die Seite J₃
der quadratischen Halsmündung = 0,m316 und
B = 0,m09
gefunden wurde, so beträgt die Steigung einer Seitenwand im Grundrisse
(0,316 – 0,090)/2 = 0m113,
daher die Länge der Halswände = 1,m13.
Den Einlauf erhält man, indem man in Fig. 5
ca = R₁ = 0,18, cb = B = 0,09 abschneidet,
und aus a und b mit dem
Halbmesser
r = 0,957 R₁ = 0,957
. 0,18 = 0,m172
Kreisbögen beschreibt, welche sich in d schneiden. Diese Punkte sind die Mittelpunkte der beiden Kreisbögen ab des sphäroidischen Einlaufkegels.
Zu der in Fig.
1 bis 5 dargestellten Construction des berechneten Hochdruckventilators mögen
hier nachstehende Erläuterungen dienen.
Das Flügelrad besteht aus einer dünnen gußeisernen Scheibe
A von 1,m6
Durchmesser, an welche eine gußeiserne Nabe angeschlossen ist; letztere erhält gegen
die Saugöffnung die Gestalt des Einlaufkegels, der auf die so eben beschriebene Art
verzeichnet ist, und wird auf eine starke Spindel von wenigstens 0,m07 (2 1/2 Zoll) im Durchmesser aufgekeilt.
Die andere Scheibe B des Flügelrades, in welcher die
Saugöffnung sich befindet, besteht aus starkem Blech.
In diese beiden Scheiben sind die blechernen Flügel mit kurzen Zapfen festgenietet.
Um durch die Dicke der Flügel den Eintritt der Luft in den Flügelraum nicht zu sehr
zu verengen, werden die Kanten der Flügel an der inneren Peripherie zugeschärft;
überdieß wird jeder zweite Flügel gegen die innere Peripherie verkürzt. Das
Flügelrad läßt sich übrigens auch ganz in einem Stücke aus Gußeisen herstellen.
Das Gehäuse ist aus zwei Theilen D und E zusammengesetzt, deren Kränze F durch Schrauben luftdicht mit einander verbunden sind.
Die beiden Seitenwände D und E sind dem Flügelrade entsprechend tellerförmig vertieft, so daß die
inneren Seitenwände der Flügelscheiben und des Gehäuses in eine Flucht fallen, und
beide daher gleich weit abstehen. An die Seitenwand E
ist der kurze Einlaufhals G angegossen, sein innerer
Durchmesser stimmt mit jenem der Saugöffnung überein und mißt 0,m36.
Das Flügelrad schließt sich im Bereiche der Saugöffnung an die Wand E des Gehäuses an. Zu diesem Ende ist die in der Scheibe
B angebrachte Saugöffnung mit einem schmiedeeisernen abgedrehten Ringe
von 0,m020 Breite eingefaßt, welcher in
einer entsprechenden ringförmigen und gleichfalls abgedrehten Vertiefung der
Seitenwand E spielt, ohne sie wirklich zu berühren.
Dieser Anschluß findet jedoch nur in einer auf die Achse senkrechten Ebene statt,
und nicht an der äußeren Peripherie des Ringes, um welche vielmehr ein Spielraum von
etwa 0,m010 freigehalten wird. Die normale
Stellung der beiden Schlußflächen erzielt und regulirt man mittelst einer
Stellschraube m (Fig. 2) und einer Feder
l, welche beide eine kleine Verschiebung der Spindel
S in der Richtung der Achse zulassen, und einander
entgegenwirken. Es muß sorgfältig darauf gesehen werden, daß zwischen den beiden
Schlußflächen kein gegenseitiger Druck stattfinde, welcher zu einem unnöthigen
Arbeitsaufwand in Folge der Reibung Veranlassung geben würde.
Diese Art der luftdichten Verbindung des Flügelrades mit dem Gehäuse ist leicht
herzustellen, da sich der luftdichte Schluß bloß auf einen Ring von nur 0,m36 im Durchmesser bezieht; es unterliegt
aber auch keinem Anstande, diesen luftdichten Schluß für die Dauer zu erhalten, weil
die beiden gegen einander gekehrten Flächen sich nicht berühren, also sich auch
nicht wechselseitig abnutzen, sondern nur möglichst nahe neben einander laufen. Eine
allmähliche Abnutzung der Spindellager beirrt nicht die Genauigkeit dieses
Abschlusses, weil hierbei bloß eine gegenseitige Verschiebung der beiden Flächen in
verticaler Richtung stattfindet. Das erste Zusammenpassen dieser Flächen kann durch
Anwendung von Schmirgel sehr leicht erzielt werden.
Auch an der Rückseite des Flügelrades wird dessen Anschluß an das Gehäuse, und zwar
dort bewirkt, wo die Spindel oder die Nabe aus demselben heraustritt. Dieß geschieht
ganz einfach mittelst einer auf die Spindel angeschobenen Lederscheibe und eines
zweitheiligen hölzernen Ringes, welcher zwischen das Zapfenlager und das Gehäuse
eingetrieben wird, und so die Lederscheibe an letzteres anpreßt.
Das Gehäuse ruht mittelst der beiden daran angegossenen breiten und verrippten Lappen
L auf der durchbrochenen Fundamentplatte
K, die durch Schrauben an das gemauerte Fundament
festgezogen wird. Keile und Schrauben sichern die feste Verbindung der beiden Lappen
mit der Fundamentplatte und geben dem Gehäuse jene feste Stellung, welche bei
Ventilatoren von großen Durchmessern nicht genug beobachtet werden kann.
Die Spindel
S, an welcher das Flügelrad festgekeilt ist, ruht mit
ihren beiden Zapfen auf den Lagerständern G und H, die gleichfalls auf der gemeinschaftlichen
Lagerplatte K festgekeilt und verschraubt sind.
Es ist von Wichtigkeit, die Lagerschalen recht lang zu machen, um den Spindelzapfen
eine größere Auflagfläche darzubieten; in der Zeichnung sind die Lager 0,m16 oder 6 Zoll lang gehalten. Auch ist es
vortheilhaft, den Lagerschalen überdieß von Außen die Kugelform zu geben, und
darnach auch ihren Sitz zuzurichten, weil hierdurch das gleichmäßige Aufliegen der
Zapfen ihrer ganzen Länge nach gesichert wird.
Die Treibrolle
R läßt sich ganz zweckmäßig auf der angegebenen Stelle
aufkeilen, wenn dort die Spindel verstärkt wird.
Bei t wird der Blasehals mit der gleichweiten Windleitung
in Verbindung gebracht, welche bei schwacher Windpressung bloß aus Ziegelmauerwerk
bestehen kann, und dann nach allen Seiten mit Letten umstaucht wird. Für stark
gepreßten Wind erhält die Windleitung einen kreisförmigen Querschnitt, und wird aus
gußeisernen oder blechernen Röhren angefertigt; in letzterem Falle läßt man den
rechteckigen Querschnitt des Auslaufhalses bei q
allmählich in einen kreisförmigen übergehen, und gibt dem gußeisernen Blasehalse zu
diesem Behufe die entsprechende pyramidal-conische Form. Der äußere
Durchmesser des Blasehalses muß dann vermöge (14) 0,m356 betragen.
Die Verbindung bei q und t
läßt sich einfach mittelst eines Muffes und einer Holzverkeilung
bewerkstelligen.
Soll das Flügelrad aus dem Gehäuse herausgenommen werden, so hat man bloß die vordere
Wand E desselben von der rückwärtigen Wand D abzuschrauben, und die Treibrolle R loszuketten; es läßt sich dann das Rad sammt Spindel
in der Richtung ihrer Achse herausziehen. Einen bequemen Zutritt für diese Arbeit
gewährt in diesem Falle die Fundamentgrube W.
Der in Fig.
1–5 dargestellte Ventilator unterscheidet sich in mehreren Punkten
wesentlich von den gewöhnlich angewendeten Ventilatoren, und zwar:
a) durch seine kleine
Saugöffnung;
b) durch seine geringe Breite;
c) durch seine einwärts gekrümmten und
radial auslaufenden langen Flügel;
d) durch den Bau des spiralförmigen
Mantels;
e) durch den luftdichten Anschluß des
Flügelrades an das Gehäuse an der Seite der Saugöffnung mittelst eines Ringes
von geringem Durchmesser;
f) durch die Anwendung eines besonderen
Blasehalses von pyramidaler oder conischer Gestalt;
g) durch mehrere Eigenthümlichkeiten in
den Details.
Tafeln