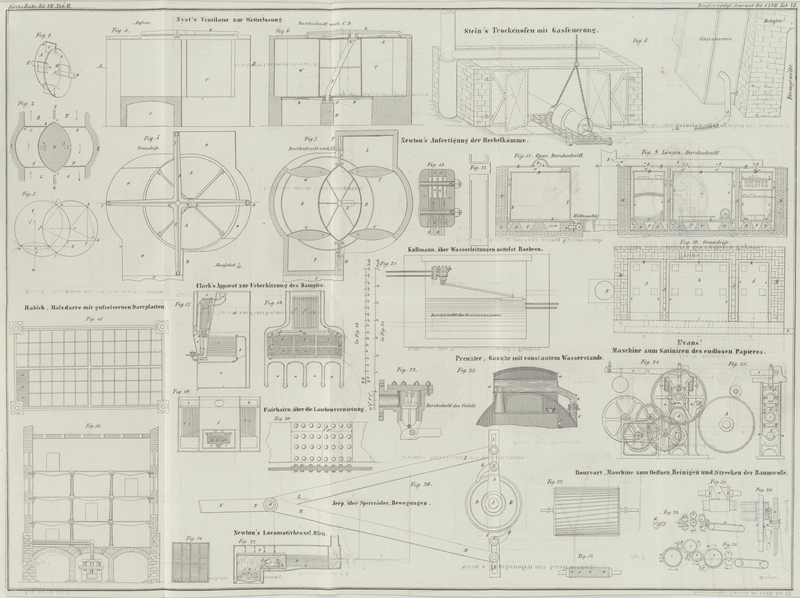
| Titel: | Neuer Ventilator für die Wetterlosung; von Fr. Nyst in Lüttich. |
| Fundstelle: | Band 157, Jahrgang 1860, Nr. CIV., S. 418 |
| Download: | XML |
CIV.
Neuer Ventilator für die Wetterlosung; von
Fr. Nyst in
Lüttich.
Aus der Revue universelle des mines, März und April 1860,
S. 326.
Mit Abbildungen auf Tab.
VI.
Nyst neuer Ventilator für die Wetterlosung.
Eine der interessantesten Fragen für den Bergmann ist ohne Zweifel diejenige der
Zuführung von Wettern in die Gruben, d.h. die Herstellung eines Luftzuges, welcher
hinreichend stark ist, um die irrespirabeln Gase in dem Maaße zu verdünnen und
fortzuführen als sie entstehen. Die Wetterversorgung ist nicht nur ein wichtiger
Theil des Grubenhaushaltes und der Schwierigkeiten des Grubenbetriebes bei großen
Teufen, sondern auch ein Gegenstand der Humanitätsrücksichten.
In einer Grube mit schlechten Wettern werden die Grubenhölzer sehr bald zerstört und
die Lichte brennen schlecht. Der Arbeiter empfindet Beängstigung, welche durch die
eingetretene Erhöhung der Temperatur vermehrt, die Arbeiten erschwert und so
nachtheilig auf das Arbeitsquantum wirkt. Endlich ist derselbe den größten Gefahren,
wie z.B. der traurigen Krankheit des Blutmangels dem Erstickungstode und den
Explosionen ausgesetzt.
Die Wichtigkeit einer gehörigen Ventilirung der Gruben ist in Belgien lebhaft
empfunden und die Mehrzahl der tiefen Gruben ist mit den erforderlichen Apparaten
versehen worden.
Die Mittel zur Hervorbringung der Ventilirung sind sehr zahlreich. Sie zerfallen in
zwei große Kategorien:
1) in solche, welche durch Erhitzung der Luft, und
2) in solche, welche mechanisch wirken.
Die Erhitzung der Luft (sogen. Wetteröfen) scheint in England gute Resultate zu
geben, wo die Strecken einen großen Querschnitt haben, aber in Belgien ist dieses
Mittel als durchaus unzulänglich befunden und bei den Gruben mit schlagenden Wettern
selbst verboten worden. So kommt es denn, daß während in England fast nur Wetteröfen
angewendet werden, diese bei den Steinkohlengruben des Continentes allmählich durch
mechanische Ventilirungen verdrängt worden sind.
Diese mechanischen Ventilirungen bestehen
a) in pneumatischen Maschinen,
b) in Ventilatoren mit Centrifugalkraft,
c) in Maschinen mit übertragener Bewegung,
d) in rotirenden Pumpen.
Ein jedes dieser Systeme hat Vortheile und Uebelstände, woraus folgt, daß man für
jeden speciellen Fall eine besondere Wahl zu treffen hat.
Die Maschinen welchen der Vorzug gegeben wird, sind die rotirenden Pumpen oder
pneumatischen Räder (Aspiratoren), und unter diesen ist der Ventilator von Fabry der verbreitetste.Man zählt gegenwärtig in Belgien mehr als 60 solche Ventilatoren. (Derselbe
ist beschrieben im polytechn. Journal Bd.
CXXX S. 336.) Diese sinnreiche Maschine verdient auch in jeder Beziehung den Vorzug,
welchen man ihr ertheilt. Indessen ist sie nicht ohne Unvollkommenheiten. Die
Schwierigkeiten der Adjustirung, welche ihre Construction darbietet, machen sie sehr
kostspielig und die starke Abnutzung der Zahnräder oder Zapfenlager veranlaßt
nachtheilige Stöße.
Der neue Ventilator ist eine rotirende Pumpe und scheint
uns mehrere Vortheile darzubieten, welche wir im Verlauf der Beschreibung erörtern
werden.
Princip, auf welchem diese Maschine
beruht.
Man stelle sich ein Rad vor, dessen Schaufeln anstatt in fester Lage gegen das
Centrum zu verharren, eine zweite Bewegung haben, welche bewirkt, daß sie mit sich
parallel bleiben; die Punkte dieser Schaufeln in verschiedenen Entfernungen von der
Achse werden gleiche Peripherien beschreiben, deren Mittelpunkte aber alle
verschieden sind und sich in einer geraden, zu den Schaufeln parallelen Linie
befinden. Aus dieser Bewegung geht hervor, daß der Inhalt des Raumes zwischen zwei
Schaufeln in zwei verschiedenen Stellungen sehr verschieden seyn wird.Man sehe den unten folgenden mathematischen Beweis dieses Princips. Auf dieser Verschiedenheit der Volume beruht die ganze Construction des
Ventilators.
Bewegung der Schaufeln.
Die erforderliche Bewegung wird den Schaufeln auf folgende Weise ertheilt.
Zwei gleiche und parallelstehende Scheiben A und B, Fig. 1, drehen sich um
zwei parallele, und in einer verticalen Ebene unter
einander liegende Achsen D und E.
Die beiden Scheiben haben dieselbe Anzahl von gleich weit von einander abstehenden
Löchern, und in diesen Löchern drehen sich Zapfen, welche am Ende der Diagonale
einer Schaufel angesetzt sind und der großen Achse derselben parallel liegen.
So tritt der Zapfen a der Schaufel C in das Loch a der Scheibe A, und der Zapfen b
derselben Schaufel tritt in das Loch b der Scheibe B. Wenn nun die beiden Scheiben gleichzeitig und gleich
schnell sich drehen, wird der Punkt b einen Bogen um den
Mittelpunkt β beschreiben und der Punkt a wird denselben Bogen um den Mittelpunkt α beschreiben, und da diese beiden Punkte
dieselbe Bewegung machen, so wird die Schaufel immer parallel mit sich selbst
bleiben.
Zwischen beiden Scheiben sitzen vier unter einander parallele Schaufeln.
Benutzung dieser Bewegung.
In Fig. 2,
welche einen senkrechten Durchschnitt durch die Achsen darstellt, sind die Schaufeln
durch C, D, E und F
dargestellt. Der Zapfen b der Schaufel C sitzt in der Scheibe welche sich um β dreht, und ihr Zapfen a sitzt in der Scheibe welche um α sich
dreht.
Nun sey H ein festliegender Kern, und I und K seyen zwei
Seitenwände, welche an die Schaufeln genau herantreten. Wenn nun die Bewegung in dem
Sinne, welchen die Pfeile bezeichnen, stattfindet, so wird, sobald die Schaufel E die Stellung der Schaufel C annimmt, die Schaufel F die frühere Stellung
der Schaufel E einnehmen, und da diese bei ihrem
Fortschreiten von E bis C
stets an die Umgebung sich eng angeschlossen hat, so wird eine Communication zwischen der äußeren Luft
M und der Grubenluft L
verhindert. Derselbe Vorgang vollzieht sich an der anderen Seite des Kernes. Die
Schaufeln saugen daher bei ihrer Bewegung die Grubenluft durch die Oeffnungen L und N an, und stoßen sie
durch die Oeffnungen M und O
in die freie Luft aus.
Gestalt der Schaufeln.
Wenn die Schaufeln an den Enden i und i' des Kernes vorüberstreichen, müssen sie stets mit
diesen Kanten in Berührung bleiben, damit die äußere Luft in die Räume L und N nicht eintritt.
Dieses läßt sich nur dadurch erreichen, daß den Schaufeln eine gewisse Krümmung
gegeben wird, deren Bestimmung in folgendem Satze enthalten ist:
Eine gerade Linie mn (Fig. 3) bewege
sich parallel zu ef in der Weise, daß m stets im Kreise e und n im Kreise f bleibt;
welches ist die krumme Linie, die während der ganzen Bewegung der Schaufel durch den
Punkt i (der fest liegt) und durch m und n geht?
Denken wir uns die gerade Linie mn festliegend und
die Kreise f und e
beweglich, so daß fe immer parallel zu mn bleibt und daß die Kreise f und e während der ganzen
Bewegung respective durch die Punkte m und n gehen, so wird an der Aufgabe nichts geändert und die
gesuchte Curve wird durch den Punkt i beschrieben
werden.
Nehmen wir nun als Achse der Größen x die gerade Linie
mn und als Achse der Größen y die Senkrechte in deren Mitte an. Es seyen x und y die Coordinaten des
Punktes i, α und β diejenigen des Centrums e, und α' und β'
diejenigen des Centrums f.
Die Bedingung, daß i stets in den Kreisen e und f sich befindet, wird
erfüllt seyn, wenn:
(I) (x
– α)² + (y – β)² = R²,
(II) (x
– α')² + (y – β')² = R².
Bedingung des Parallelismus zwischen mn und ef ist, daß:
(III) β = β'.
Die Mittelpunkte e und f
müssen in der Entfernung R bleiben:
(IV). (α
– α')² + (β – β')² = R².
Endlich geht der Kreis e immer durch den Punkt m, für welchen 0 die Abscisse und 1/2 R die Ordinate ist.Die Bedingung, daß der Kreis f immer durch den
Punkt n geht, ist in den Bedingungen des
Parallelismus von mn und ef und der gleichbleibenden Entfernung
zwischen f und e
einbegriffen.
(V) (1/2 R – α)² + β² = R².
Diese Gleichungen zusammen enthalten die nothwendigen und hinreichenden Bedingungen
um die Bewegung zu bestimmen.
α, α', β und β' sind die Größen, welche
die Lage der Kreise feststellen; wenn man sie eliminirt, so erhält man ein
Verhältniß zwischen x und y
und der bekannten Größe R, ein Verhältniß, welches die
Gleichung der gesuchten Curven seyn wird.
Substituirt man den durch (III) gegebenen Werth von β', so werden die Gleichungen (I), (II), (IV) und (V):
(I') (x
– α)² + (y – β)² = R²
(II') (x
– α')² + (y – β)² = R²
(IV') (α
– α')² = R²
(V') (1/2 R –
α)² + β² = R²
(IV') gibt als Werth für α'
α' = α – R.
Aus Gleichung (I') und (II) finden wir den Werth von α:
α' = x + 1/2 R,2x (α – α') –
(α² – α'²) – (α² – α'²) = 02x (α – α') –
(α + α') (α – α') = 02x = α + α' 2x = 2α – R
also: α' = x – 1/2 R.
substituiren wir diesen Werth in Gleichung (V'), so bekommen wir für β:
= ± √(R² – x²).β² = 3R²/4 + Rα – α²β² = 3R²/4 + Rx +
R²/2 – x² – xR – R²/4β² = R² – x²
Substituirt man endlich diese Werthe von α und β in Gleichung (I'), so erhält man die
Gleichung:
(x – x – 1/2 R)² + (y ∓ √(R² – x²))² = R²,
welche nach verschiedenen Operationen die Gleichung der Curve
gibt:
x² + (y ∓ R/2 √3)² = R².
R²/4 + y² ∓ 2y √(R² – x²) + R² – x² = R²y² – x² + R²/4 = ± 2y √(R² – x²)y⁴ – 2x²y² +
y²R²/2 + x⁴ – x² R²/2 + R⁴/16 = 4y²R²
– 4y²x²x⁴ + 2x² – R²x²/2 + y⁴ – R²y²/2 + R⁴/16 = 3R²y²x² + y² – R²/4 = ± Ry√3x² + y² ∓ Ry√3 – R²/4 =
0x³ + y³ ± Ry√3 – 3R²/4 =
0
Diese Gleichung repräsentirt zwei Kreise vom Halbmesser R. Der Kreis x² + (y – R/2 √3)² =R² entspricht der Bedingung für den Punkt i, und der Kreis x² + (y + R/2 √3)² = R² für den Punkt i'.
Die Schaufel wird also gebildet werden müssen durch zwei Kreisbogen von demselben
Radius als f und e, deren
Mittelpunkt in der auf der Mitte der Linie mn
errichteten perpendicularen Linie und in einer Entfernung gleich R²/2 √3 liegt. (Dieses bestätigt sich
durch die Construction, da die Linie mn = dem
Radius, und folglich die Seite eines eingezeichneten Sechsecks, und da R/2√3 ihre Entfernung vom Mittelpunkte ist.)
Theoretisches Volumen.
Suchen wir jetzt das erzeugte Volumen. Es wird gleich seyn zweimal dem zwischen zwei
Schaufeln enthaltenen Luftvolum, im Augenblicke wo eine Schaufel aufhört oder die
andere anfängt zu saugen, und da während eines Umganges diese Stellung viermal
wiederkehrt, so ist das bei jeder Umdrehung gesogene Luftquantum gleich dem
achtfachen Volum zwischen zwei Schaufeln.
Dieses Volum ist gleich der Oberfläche abcd (Fig. 3),
multiplicirt mit der Entfernung l den beiden Scheiben.
Die Oberfläche abcd ist gleich dem Sector bed
plus den beiden Parallelogrammen abef und fecd, minus dem Sector afc. Aber der Sector fac ist gleich dem Sector bed, die
Oberfläche ist daher gleich der Summe der beiden Parallelogramme abef und dcef,
also:
Oberfläche abcd = fe × gb
Oberfläche abcd = fe × bd
sin α.
Diese Oberfläche ist für verschiedene Stellungen der Schaufeln verschieden. Da fe und bd
constant sind, so wird sie mit dem sin α sich
ändern; sie wird am größesten seyn, wenn α =
90°, und am kleinsten, nämlich = 0, wenn α
= 0.
Wird der Gangraum so gestaltet, daß die Oberfläche abcd am größesten ist, so haben wir:
Oberfläche abcd = fe × bd.
Da wir aber fe = R und
bd = r√2
der Seite eines eingezeichneten Quadrates genommen haben, so erhalten wir:
Oberfläche abcd = R²√2.
Das pro Umgang ausgesogene Volum ist daher = 8 l R²√2.
Bringt man die Dicke der Schaufeln in Anschlag, so muß man von der Oberfläche abcd zweimal das Segment nomp abziehen, welches = ist dem Sector o''npm, minus dem Dreiecke
o''nm, nämlich:
R/2 × 2πR/6 – R/2 oo''Weil oo“ die Entfernung der Seite des
Sechsecks vom Mittelpunkte oder die Hälfte der Seite eines eingezeichneten
Dreiecks ist.
oder πR²/6 – R²√3/4 = (2π – 3√3)/12 R² =
1,087/12 R².
Das pro Umgang gesogene Luftvolum ist demnach:
8lR² (√2 –
1,087/12).
Drei Schaufeln würden ebenfalls genügen. Dann erhielte man als pro Umgang geschöpftes Luftquantum nur das sechsfache Volumen zwischen
zwei Schaufeln, aber bd würde = R²√3, der Seite eines eingezeichneten
Dreieckes seyn, so daß das pro Umgang erfolgende Volumen
wäre:
6lR² (√3 –
1,087/12),
ein geringerer Werth als der vorige.
Wenn man sechs Schaufeln nähme, würde das Volumen größer ausfallen, nämlich:
12lR² (1 –
1,087/12),
wir glauben aber, daß eine geringere Anzahl vorzuziehen ist,
damit es nicht zu viele bewegliche Theile gibt.
Vergleich mit dem Ventilator von
Fabry.
Wir wollen nun das ausgesogene theoretische Luftquantum mit demjenigen eines Fabry'schen Ventilators von gleichen Dimensionen
vergleichen; der Correctionscoefficient für das theoretische Volumen zur Bestimmung
des effectiven ist für beide Maschinen gleich anzunehmen, wie wir später beim
Nutzeffecte nachweisen werden.
Es sey bei einem Fabry'schen Ventilator
R
= 1,70 Meter
r
= 1,00 „
l
= 2,00 „
Das pro Umdrehung ausgesogene Luftquantum ist
demnach:
V = 2t
(3,14 R² – 3,402 r²) = 22,690 Kubikmeter
und bei 30 Umdrehungen pro
Minute:
V' = 680,70 Kubikmeter.
Bei einem Nyst'schen Ventilator sey:
R
= 1,70 Meter,
l
= 2,00 „
dann beträgt die pro Umdrehung
geschöpfte Luftmenge:
V = 8lR² (√2 – 1,087/12) = 62,128 Kubikmeter
und pro Minute bei 30
Umdrehungen:
V' = 1863,84 Kubikmeter.
Dieses Volumen ist mehr als zwei und ein halbes Mal so groß als das von einem Fabry'schen Ventilator von gleichen Dimensionen
gelieferte.
Reducirt man die Geschwindigkeit auch auf die Hälfte (15 Umgänge), so ist das dabei
erhaltene Volumen noch viel größer als dasjenige des Fabry'schen Ventilators (30 Umgänge), nämlich 931,42 Kubikmeter.
Wenn der Ventilator nur drei Schaufeln hätte, so würde das ausgesogene Volumen pro Umdrehung sich belaufen auf:
V = 6lR²√3 = 59,99 Kubikmeter
und pro Minute
V' = 2080,80 Kubikmeter,
nämlich über dreimal mehr als dasjenige des Ventilators von
Fabry.Bei der Berechnung dieser beiden letzten Volume ist die Dicke der Schaufeln
nicht berücksichtigt worden, wie bei dem Fabry'schen Ventilator.
Nutzeffect.
Das theoretische Luftvolumen Q ist = Vn/60. Das effective wird weit kleiner ausfallen, weil
die Luft durch den Raum zwischen den Schaufeln und dem Canal derselben wieder
eintritt. Es sey:
S der Querschnitt dieses Zwischenraumes,
K der Contractionscoefficient,
H der Unterschied der Luftpressung,
dann tritt pro Secunde eine
Luftmenge wieder ein, welche proportional ist:
KS√2gH.
Das effective Luftvolumen ist demnach:
Q – KS√2gH = Q'.
Das mechanische Moment wird = seyn dem theoretischen Volumen der ausgesogenen Luft,
multiplicirt mit dem Unterschiede der Pressung plus der
Reibung auf den Zapfen, also Q (H + h').
Die effective Leistung ist gleich dem Volumen der ausgesogenen Luft, multiplirt mit
dem Unterschiede der Pressung, also Q'H.
Der Nutzeffect ist folglich:
Textabbildung Bd. 157, S. 426
Man ersieht hieraus, daß der Nutzeffect mit Q steigt, und
da diese Formel eben so gut auf die neuen Ventilatoren als auf den Fabry'schen Ventilator anwendbar ist, so sieht man auch,
daß der Nutzeffect bei den erstern weit größer seyn wird, denn S wird nahezu bei beiden gleich und h' wenig verschieden seyn.
Bei dem Fabry'schen Ventilator tritt eine schädliche
Luftmenge bei jedem Vorübergange eines Zahns ein und zwar in einem derjenigen der
Grubenluft entgegengesetzten Sinne; dadurch entstehen Stöße, Wirbel und
Kraftverluste. Dieses ist bei dem in Vorschlag gebrachten Ventilator nicht der Fall
und selbst die Schaufeln stoßen die Luft nicht, da sie dieselbe so zu sagen bis zu dem
Augenblick in welchem solche gefaßt ist, nur abschneiden.
Einzelheiten der
Construction.
Wie bei dem neuen Ventilator von Lemielle
Beschrieben im polytechn. Journal Bd. CL.
S. 194. ist die Achse E (Fig. 4, 5, 6 und 7) vertical gestellt. Ihr
unteres Ende steht in einer auf dem gemauerten Fundamente M befestigten Pfanne S und ihr oberes Ende
wird von dem Kreuze K gehalten, welches mit dem Mantel
O zusammengegossen ist. Sie hat an diesem ihrem
oberen Ende einen Bund N, auf welchem die Scheibe A sich dreht, während die untere Scheibe B auf der Pfanne S sich
dreht, in welcher die Achse derselben mit dem einen Ende liegt. Die Luft tritt durch
den Canal G unter der untern Scheibe ein und von da
steigt sie durch die Oeffnungen L und P nach dem Raume zwischen den Schaufeln.
In dem Mauerwerke F und H
befinden sich 2 Gleit- oder Liederungsstücke f
und h, welche mittelst einer Feder oder eines
Gegengewichtes gegen die Kante des Kernes getrieben werden und die Communication
zwischen der äußern Luft und den Räumen L und P abschneiden. Die Schaufeln treten wie ein Keil
zwischen den Kern und die Gleitstücke, welche zurückweichen. (Wir haben früher
gesehen, daß die Luft durch einen Raum zwischen der Schaufel und dem Kerne nicht
wieder eintreten kann.)
An der oberen und unteren Seite vor jedem Gleitstücke sind zwei kleine Rollen
angebracht, welche die gleitende Reibung in eine rollende verwandeln. Man würde
diese Gleitstücke auch durch Excentrica in Bewegung setzen können.
Es sey noch erwähnt, daß bei einem kleinen Modelle, welches wir ausgeführt haben, die
eine gedrehte Scheibe die andere zwar ganz gut mit fortzieht, daß es aber
vorzuziehen seyn dürfte, jeder der beiden Scheiben Bewegung zu ertheilen.
In Betreff der übrigen Einzelheiten verweisen wir den Leser auf die Fig. 4, 5, 6 und 7 (welche indessen nur als
Entwurf zu betrachten sind); wir behalten uns vor, auf diesen Gegenstand
zurückzukommen, sobald ein vollständiges Modell zur Ausführung gelangt seyn wird und
Versuche auf eine unzweifelhalte Weise die Vortheile erwiesen haben, welche diese
Maschine darzubieten scheint und die Modificationen ermittelt seyn werden, welche in
deren Construction anzubringen seyn möchten.
Tafeln