| Titel: | Ueber die Ausflußcoefficienten der Wassergerinne, welche in der Gemeinde Remscheid und deren Umgegend bei Hammerwerken und Schleifkotten gebräuchlich sind, über die Wirkung der Hammerräder und einzelne zweckmäßige Umänderungen an Hammer- und Schleifwerkstätten; von Rob. Röntgen. |
| Autor: | Robert Röntgen [GND] |
| Fundstelle: | Band 158, Jahrgang 1860, Nr. I., S. 1 |
| Download: | XML |
I.
Ueber die Ausflußcoefficienten der Wassergerinne,
welche in der Gemeinde Remscheid und deren Umgegend bei Hammerwerken und Schleifkotten
gebräuchlich sind, über die Wirkung der Hammerräder und einzelne zweckmäßige
Umänderungen an Hammer- und Schleifwerkstätten; von Rob. Röntgen.
Mit Abbildungen auf Tab.
I.
Röntgen, über die Ausflußcoefficienten der Wassergerinne, welche
bei Hammerwerken und Schleifkotten in Remscheid gebräuchlich sind.
In der Gemeinde Remscheid und deren nächster Umgegend ist besonders die Eisen- und Stahlwaaren-Industrie zu Hause. Es befinden sich hier auf einem
Flächenraume von etwa 2/3 Quadratmeilen nicht weniger als 200 Hammerwerke und
Schleifkotten, die hauptsächlich zur Darstellung des Raffinirstahls und zum
Schleifen und Poliren derjenigen Werkzeuge dienen, welche in den Kleinschmiedereien
der gedachten Gemeinde und einigen angrenzenden kleineren Ortschaften fabricirt
werden. Nur einige wenige Hämmer werden auch zum Breiten der Sägen und Sensen
benutzt. Die Gewerke erhalten ihr Betriebswasser von zwei größeren und mehreren
kleineren Bächen, von denen sich die letzteren in die ersteren ergießen. Der eine
größere Bach bildet die nördliche und westliche, der andere die östliche und
südliche Grenze der Gemeinde.
Die sämmtlichen Wassergerinne der Hammerwerke und Schleifkotten sind von derselben
Construction. Nur bei denjenigen Kotten, welche unterschlägig betrieben werden, hat
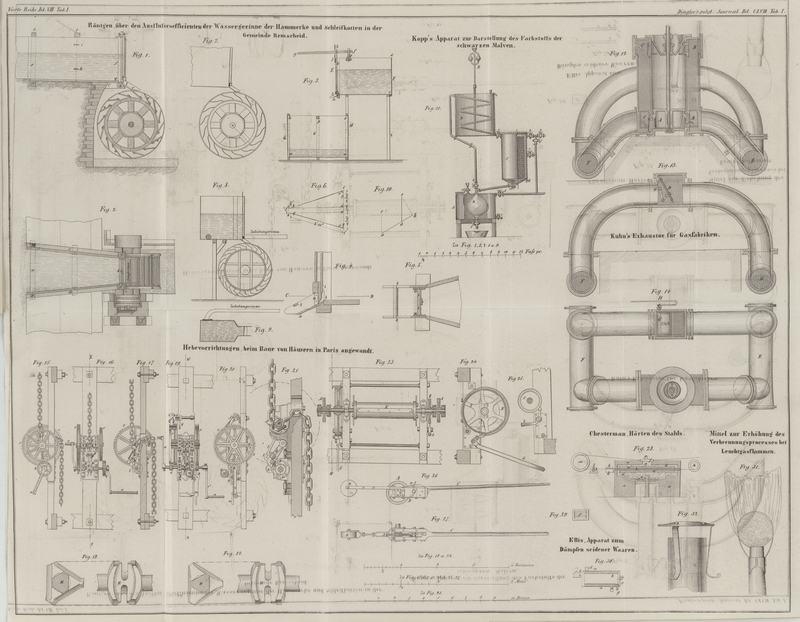
die Schußrinne eine größere Neigung als bei den übrigen Gewerken. Fig. 1 zeigt den genauen
Durchschnitt eines oberschlägigen Hammerrades nebst dem dazu gehörigen
Wassergerinne, welches man hier zu Lande wohl Eishaus zu
nennen pflegt. Die Räder haben durchschnittlich einen Durchmesser von 8 Fuß, selten
steigt derselbe bis zu 9 Fuß und in noch selteneren Fällen wird er kleiner als 8 Fuß
genommen. Die lichte Weite beträgt bei den älteren Rädern 2 2/3 bis 3 1/4 Fuß, erst
in neuerer Zeit hat man angefangen hier und da Räder von 3 Fuß 9 Zoll bis zu 4 Fuß
Weite zu bauen. Die Radkränze macht man in der Regel 10 Zoll bis 1 Fuß tief. Fast alle Räder haben 16
Schaufeln, deren Richtung mit dem Radhalbmesser an der äußeren Peripherie einen
Winkel von 41 bis 42 Grad einschließt.
Die älteren Wassergerinne bestehen noch sämmtlich aus Holz, die neueren jedoch sind
aus dicken, steinernen Platten zusammengesetzt, von denen vier die beiden
Seitenwände und zwei den Boden des Gerinnes bilden; die Vorderwand besteht jedoch
auch hier, wie bei den ältern Gerinnen, aus etwa 1 1/2 Zoll dicken Bohlen. Die
Platten, welche etwa eine Dicke von 3 Zoll besitzen, werden durch ein einfaches
Zimmerwerk zusammengehalten. Dasselbe besteht zunächst aus den vier Grundschwellen
a, b, c und d, Fig. 2, welche
ein Trapez bilden, sodann aus den verticalen Pfosten e, f,
g und h, welche in die ersteren eingezapft und
die oben durch horizontale Balken s und t, Fig. 1, verbunden sind.
Die Platten werden durch eiserne Klammern i, k
festgehalten und die Fugen zwischen je zweien mit einem wasserdichten Kitt
ausgefüllt. Die Länge der Gerinne beträgt durchschnittlich 12 Fuß, hinten sind sie 5
Fuß bis 5 Fuß 6 Zoll weit und die vordere Weite richtet sich nach der Breite des
Rades, die man etwa 5 bis 6 Zoll größer nimmt als die des Gerinnes. Die Schußrinne
q, r ist auf der vorderen, etwas abgeschrägten
Grundschwelle b befestigt und bildet mit dem Horizont
einen Winkel von 28 bis 32 Grad. Das Schutzbret n von
etwa 3 Zoll Dicke, ist unten mit einer zugeschärften Kante versehen, mit welcher es
auf der Schußrinne ruht. Diese Kante liegt durchschnittlich 4 bis 5 Zoll tiefer als
der Boden des Gerinnes bei q. Letzterer ist geneigt und
liegt hinten mehrere Zolle höher als vorne. Die Länge der Schußrinne ist
verschieden, bei einigen Hammerwerken beträgt sie nur 1 Fuß, bei anderen 3 1/2 bis 4
Fuß; dieß richtet sich besonders nach dem Gefälle, welches etwa zwischen 13 und 20
Fuß variirt. Bei einem Gefälle von 20 Fuß gibt man dem Rade eine Höhe von 9 1/2 Fuß,
nimmt etwa 5 Fuß für die senkrechte Höhe der Schußrinne und 5 1/2 Fuß für die
Druckhöhe im Gerinne.
Die Wirkung der hiesigen, sowie auch der märkischen Hämmer, die sich besonders auf
der Ennepe und Volme, zweien Nebenflüssen der Ruhr, befinden, ist, so viel ich weiß,
zuerst von dem verstorbenen Geh. Rath Professor Dr.
Egen genauer untersucht worden. Er bediente sich hierzu
eines Dynamometers, dessen Bremse aus einem gegliederten Eisenbleche bestand,
welches um die Welle gelegt und vermittelst Schraubenmuttern fest angezogen werden
konnte. Der gewöhnliche Prony'sche Zaum hätte sich hier
nicht wohl anwenden lassen, weil zwischen der Welle und dem Boden des Gebäudes zu
wenig Raum vorhanden ist. Egen's Untersuchungen über
diesen Zweig der Mechanik sind in dem von ihm herausgegebenen Werke: „Untersuchungen
über den Effect einiger in Rheinland-Westphalen bestehenden
Wasserwerke“ (Berlin, gedruckt bei A. Petsch), enthalten. Es heißt dort S. 82: daß der Ausflußcoefficient für
sämmtliche Hammerwerke zu 0,80 angenommen worden sey und zwar, wie an einer andern
Stelle angegeben ist, weil die Gerinne mit denen für die Poncelet'schen Wasserräder am meisten Aehnlichkeit hätten. Die Zahlen
jedoch, welche man für die Wasserconsumtion pro Secunde
aus der Druckhöhe und dem Inhalte der Schützenöffnung berechnet hat, beweisen, daß
der Coefficient 0,72 der Rechnung zu Grunde gelegt wurde. Weßhalb diese 8 Procent
abgezogen sind, finde ich an keiner Stelle angegeben.
Wenn nun auch die Poncelet'schen Gerinne mit denen der
hiesigen Gewerke in manchen Punkten übereinstimmen, so sind sie doch auch in
anderen, die besonders auf den Ausflußcoefficienten influiren können, von diesen
ziemlich verschieden. Während bei den ersteren die vordere Wand des Gerinnes eine
Neigung von 45 bis 63 1/2 Grad gegen den Horizont hat, steht sie bei den letzteren
senkrecht, und während bei jenen die Schußrinne etwa um 12 bis 14 Grad geneigt ist,
beträgt diese Neigung bei den anderen 28 bis 32 Grad; hierzu kommt noch, daß bei den
hiesigen das Schutzbret auf der stark geneigten Schußrinne steht.
Ob also die Ausflußcoefficienten für beiderlei Gerinne dieselben sind oder nicht,
konnte nur durch Versuche entschieden werden. Daß aber eine solche Entscheidung für
die Ermittelung der Wassermenge, welche in einer gewissen Zeit durch die
Schützenöffnung fließt und damit gleichzeitig für die genaue Berechnung des
Nutzeffectes der Räder, welche durch jenes Wasser betrieben werden, nothwendig ist,
müssen wir hier als bekannt voraussetzen. – Ich habe es deßhalb unternommen,
durch eine Reihe von Versuchen den Ausflußcoefficienten für die hiesigen Gerinne bei
Hammerwerken und Schleifkotten zu bestimmen, um darnach für die verschiedenen
Beobachtungen, welche Hr. Egen im Jahre 1828 an einem
Hammer auf der sogenannten Müggenbach in der Gemeinde Remscheid angestellt hat, und
die in dem eben citirten Werke aufgeführt sind, die Wassermenge und den Nutzeffect
der Hammerräder zu berechnen. Meine Arbeit zerfällt demnach zunächst in zwei Theile.
Der eine handelt über die Bestimmung der Ausflußcoefficienten, der andere über den
Nutzeffect der gedachten Räder. Hieran schließt sich noch ein dritter Theil, in
welchem ich einzelne Vorschläge zu Verbesserungen an Hammerwerken und Schleifkotten
mitgetheilt habe, die nicht allein von der Theorie gefordert werden, sondern die
auch den Grundsätzen der Praxis durchaus angepaßt sind. Die einzelnen Theile sind
mit I, II und III überschrieben.
I.
Der Apparat, den ich zu meinen Versuchen benutzt habe, war etwa 8 bis 10 mal kleiner
als die hiesigen Gerinne, nur die Länge und Höhe desselben betrug 1/4 bis 1/5 von
der der letzteren. Was aber die Einrichtung der Schütze und Schußrinne betrifft, so
stimmte er hierin ganz mit den hiesigen Gerinnen überein. Ein seit mehreren Jahren
mit dem Bau von Hammerwerken und Schleifkotten beschäftigter praktischer Zimmermann
hat den Apparat angefertigt. Die verschiedenen Ansichten und Durchschnitte desselben
sind in den Figuren
3, 4, 5
und 6
dargestellt.
Er besteht aus zwei hölzernen Kasten, von denen der obere E,
F,
Fig. 3, das
eigentliche Gerinne repräsentirt, der untere G, H aber
zur Ansammlung des Wassers dient, welches aus dem ersteren während des Versuchs
ausfließt. Fig.
3 stellt den verticalen Durchschnitt durch beide Kasten dar, und die Figuren 4 und
5
bezeichnen den verticalen und horizontalen Durchschnitt der Schütze und Schußrinne
in dreifacher Größe. Fig. 6 gibt endlich die genauen Größenverhältnisse des oberen
Wasserkastens oder des eigentlichen Gerinnes an. Die Aufstellung oder
Zusammensetzung des ganzen Apparates ist aus Fig. 3 ersichtlich.
Die untere Kante der Schütze h, k, i,
Fig. 3 und
4, liegt
1/2 Zoll tiefer als das vordere Ende b des Gerinnbodens.
Die Schußrinne a, b hatte bei den Versuchen eine Neigung
von 32° 20'. Das Schutzbret i, Fig. 4 und 5, ist an den Seiten so
ausgeschnitten, daß es sich wasserdicht zwischen den Leistchen u, u auf und ab bewegen kann; diese haben zusammen eine
Dicke von 2,12496 Linien und sind an die Seitenbreter s,
s der Schußrinne mit ein paar Stiftchen festgeschlagen. Dieselbe Anordnung
finden wir auch im Großen bei den Hammerwerken und Schleifkotten. Der Zwischenraum
zwischen den Leistchen u, u, die eigentliche Weite der
Schütze, betrug nach mehrmaliger genauer Messung 2,64583 Zoll und die lichte Weite
zwischen den Seitenbretern s, s 3 Zoll. Um zu erfahren
wie hoch die Schütze gezogen war, wurde an die Schützenstange i, h bei k ein in Linien und halbe Linien
getheilter Maaßstab befestigt, dessen Nullpunkt oben lag und auf den bei
geschlossener Schütze die Spitze eines Index zeigte, der dem Maaßstabe gegenüber in
dem Seitenbrete des Gerinnes befestigt war.
Der Inhalt der Schützenöffnung wird nun erhalten, wenn man die Weite mit der
senkrechten Höhe derselben multiplicirt. Auf dem Maaßstabe konnte man aber nur die
schräge Höhe ablesen. Aus der letzteren findet man indessen die senkrechte, durch
Multiplication mit dem Cosinus des Neigungswinkels der Schußrinne. Denn ist Fig. 10
abc der Winkel, unter welchem die Schußrinne ab gegen die Horizontale bc geneigt ist; bezeichnet ferner ed die schräge Höhe der Schützenöffnung: so stellt
die auf ab senkrechte Linie eb die wirkliche oder senkrechte Höhe derselben
dar. Es ist aber < bed = < abc. Man hat nun: eb = ad. cos
bed = ad. cos
abc. Da aber < abc = 32° 20' beträgt, so ist:
eb = ad. cos 32° 20' = ad . 0,8526.
Um also die wirkliche Höhe der Schützenöffnung zu finden, hat man die auf dem
Maaßstabe abgelesene noch mit 0,8526 zu multipliciren, und wenn man nur drei
Decimalstellen beibehalten will, mit 0,853.
Die Ausflußcoefficienten sind nach der Formel bestimmt worden, nach der man die Zeit
berechnet, in welcher sich ein Gefäß mit Wasser ganz oder theilweise entleert, wenn
kein Zufluß stattfindet. Bezeichnen wir die anfängliche Druckhöhe im Gefäße mit h, die nach der theilweisen Entleerung mit h₁, den Querschnitt des Gefäßes mit Q, den Inhalt der Schützenöffnung mit q, endlich die Zeit in welcher der Wasserspiegel von der
Höhe h bis zu der h₁
herabsinkt, mit s und den Ausflußcoefficienten mit c, so hat man für die Zeit:
s = 0,253 Q/(c . q) (√h – √h₁).Die Entwickelung
dieser Formel kann in jedem vollständigen Werke über Mechanik nachgesehen
werden.
Ist aber umgekehrt die Zeit s bekannt, so ergibt sich der
Ausflußcoefficient c nach der Formel:
c = 0,253 Q/(s . q) (√h
– √h₁).
Die Versuche wurden nun in der Weise angestellt, daß man zuerst den oberen Kasten E, F,
Fig. 3, bis zu
einer gewissen Höhe (h) mit Wasser füllte, dann die
Schütze zog und an einer Secundenuhr die Zeit beobachtete, welche zum Sinken des
Wasserspiegels von der Höhe h bis zu der h₁ nothwendig war. Aus diesen Stücken, der Höhe
der Schützenöffnung und dem Querschnitt des Gefäßes, läßt sich mit Zugrundelegung
obiger Formel c berechnen.
Der Querschnitt Q des Gerinnes E,
F,
Fig. 3, ergibt
sich aus den Zahlen der Fig. 6, die nach
mehrmaliger und sorgfältiger Messung erhalten worden sind.
Die Kanten f und c waren mit
Leisten xyf und xyc, deren Querschnitt ein ∆ bildet, ausgefüllt, um den Apparat an
diesen Stellen dicht zu
bekommen; die Inhalte dieser Dreiecke, sowie der Querschnitt der Schützenstange
gehen von dem Flächenraume cbahgf ab.
Die beiden Dreiecke bcd und gef sind gleich groß, denn sie haben gleiche Höhe
(bd) und gleiche Grundlinie (cd oder ef). Es
ist nun bc = 2' 11'' = 35'' und cd = 10,2187 Zoll; daher
bd = √(bc² – cd²) = √(1225 – 104,4218) = √1120,5782,
oder bd = 33,47 Zoll.
Der Inhalt der beiden Dreiecke bcd und gef ist:
bc × cd =
342,0199 Quadrtz.
Der Inhalt des Rechtecks
bdeg =
bd × ah =
100,4100 „
„ „
„ „
abgh =
ab × ah =
2,6250 „
–––––––––––––––––––––––––––––––––––––––––––
Summa:
445,0549 Quadrtz.
Hiervon geht ab:
a) Inhalt der beiden Dreiecke
xyc und xyf
= 0,3125
Quadratzoll
b) Querschnitt der Schützenstange
= 0,2344
„
––––––––––––––––––
Im Ganzen
= 0,5469
„
0,5469 Quadrtz.
–––––––––––––––––––––––––––––––––––
Differenz:
444,5080 Quadrtz.
Dieß ist der Werth von Q.
Es sind nun die Ausflußcoefficienten für 2, 3, 4, 5 und 6 Linien schräge Schützenhöhe
bestimmt worden. Wir erhalten hieraus die senkrechte durch Multiplication mit
0,8526, wie dieß S. 5 gezeigt worden ist.
Für 1''' = 0,08333... Zoll schräge Schützenhöhe ist die senkrechte
= 0,0833 × 0,8526
= 0,071 Zoll.
Hiernach beträgt die senkrechte
Höhe
für 2'''
= 0,142 „
ferner
für 3'''
= 0,213 „
für 4'''
= 0,284 „
für 5'''
= 0,355 „
für 6'''
= 0,426 „
Da die Weite der Schützenöffnung = 2,64583 oder, weniger genau, = 2,646 Zoll beträgt,
so ist der Inhalt der Schützenöffnung für 1''' = 0,071 × 2,646 = 0,188
Quadrtz., und der Werth von
0,253 . Q/q = 0,253 × 2364,4 =
598,19
Für 2''' Schützenöffn. hat 0,253 . Q/q den
Werth
299,09
„
3''' „ „
0,253 . Q/q
„ „
199,39
Für 4''' Schützenöffn. hat 0,253 . Q/q den
Werth
149,54
„
5''' „ „
0,253 . Q/q „ „
119,63
„
6''' „ „
0,253 . Q/q „ „
99,69.
In unseren Versuchen haben wir für die Druckhöhe den senkrechten Abstand des
Wasserspiegels im Gerinne bis zur Mitte der Schützenöffnung genommen. Ist die Höhe
von der unteren Kante der Oeffnung bis zur Oberfläche des Wassers = H, die senkrechte Höhe der Schützenöffnung = a, so ist die eigentliche Druckhöhe
h oder h₁ = H – 1/2 a.
Hiernach wollen wir nun die vollständige Berechnung von zwei Ausflußcoefficienten für
3 Linien schräge Schützenhöhe folgen lassen.
Nr. 1.
Schräge Höhe der Schützenöffn. = 3''', also senkrechte = 0,213''.
Druckhöhe vor dem Versuche = 7'' 9 1/2''', nach demselben 2'' 1/2'''.
Dauer der Beobachtung = 90 Secunden.
Es ist also h = 7'' 9 1/2''' = 0,6493
Fuß und h₁ = 2'' 1/2''' = 0,1701 Fuß
√h = √0,6493 = 0,806;
√h₁ = √0,1701 = 0,412,
mithin:
√h – √h₁ = 0,806 – 0,412 = 0,394.
Der Werth von 0,253 . Q/q für 3'''
Schützenöffn. beträgt 199,39; man hat daher 0,253 . Q/q
(√h – √h₁) = 199,39 × 0,394 = 78,5597. Dividiren wir dieß durch die
Dauer der Beobachtung = 90 Secunden, so erhalten wir den Ausflußcoefficienten
c = 0,873.
Nr. 2.
Schräge Höhe der Schützenöffn. = 3''', also senkrechte = 0,213''.
Druckhöhe vor dem Versuche = 8'', nach demselben 3'' 8'''.
Dauer der Beobachtung = 60 Secunden.
Es ist demnach h = 8'' = 0,6666 Fuß
und h₁ = 3'' 8''' = 0,3055 Fuß.
Ferner √h = √0,6666 =
0,816, √h₁ = √0,3055 = 0,553,
also √h – √h₁ = 0,816 – 0,553 = 0,263
und 0,253 . Q/q (√h – √h₁) = 199,39 × 0,263 = 52,439.
Dieß durch 60 getheilt, gibt für den Ausflußcoefficienten
c = 0,874.
Wir stellen nun die mittleren Werthe, welche sich aus den übrigen Beobachtungen und
Berechnungen ergeben haben, übersichtlich zusammen.
Nr.
AnzahlderVersuche.
MittlereDruckhöhein Fußen.
Höheder Schützenöffnung,
MittlererAusflußcoefficient.
GrößteAbweichung dereinzelnen
Beobachtungenvom Mittel
schrägein Linien.
senkrechte in Zollen.
1
8
0,5297
6
0,426
0,941
+ 5,5 Proc.
2
6
0,5447
5
0,355
0,926
– 5,9
„
3
6
0,5644
4
0,284
0,888
+ 3,9
„
4
9
0,4902
3
0,213
0,899
+ 5,1
„
5
6
0,4861
2
0,142
0,903
– 4,7
„
Mittel aus den Mitteln:
0,911
Erwägt man nun, daß die Versuche mit kleinen Ausflußöffnungen angestellt sind, daß
mit dem ersten Augenblicke der Zeitbestimmung die Schütze nicht gleich vollständig
geöffnet und mit dem letzten nicht momentan geschlossen war, daß ferner die
Druckhöhe nicht bis auf 1/2 oder 3/4 Linie genau ermittelt werden konnte, und
endlich, daß die Zeit nur mit Hülfe einer gewöhnlichen, aber richtig gehenden
Secundenuhr bestimmt wurde: so wird man gegen die Genauigkeit der Resultate nichts
Erhebliches einwenden können. Der mittlere Ausflußcoefficient für die hiesigen
Wassergerinne wird also zu 0,91 oder weniger genau zu 0,90 angenommen werden müssen.
Derselbe ist also um 18 Proc. größer als ihn Egen in
seinen Untersuchungen angenommen hat.
Bei genauerer Durchsicht der vorstehenden Tabelle gelangt man zu folgenden
Schlüssen.
In den drei ersten Nummern weichen die Druckhöhen nur um 1,5 bis 2 Proc. von einander
ab. Berücksichtigt man diesen geringen Unterschied nicht, so darf man annehmen, daß
die Ausflußcoefficienten abnehmen, wie die Höhen der Schützenöffnungen. Die
Coefficienten für 6,5 und 4 Linien würden sich wahrscheinlich in einem kleineren
Maaße vermindern, als in
der Tabelle, wenn die Druckhöhen vollkommen gleich wären. Bei Nr. 4 und 5 weichen
diese von denen der vorhergehenden Nummern um 7,4 bis 7,8 Proc. ab. Wären die
letzteren Druckhöhen in demselben Verhältniß größer geworden wie die ersteren, so
würden auch wohl die Ausflußcoefficienten für die letzten Nummern etwas kleiner
ausgefallen seyn. Dieß vorausgesetzt, ist es dann auf der andern Seite gewiß, daß
die Ausflußcoefficienten zunehmen, wie die Druckhöhen abnehmen. Es wird demnach die
Zuschärfung des etwa 3 Zoll dicken Schutzbretes und die Anordnung der Schußrinne mit
Schütze bei unseren Wasser-Gerinnen ähnlich wirken, wie cylindrische oder
parallelepipedische Ansatzröhren, die auch einen um so größern
Ausfluß-Coefficienten geben, je kleiner die Druckhöhe ist.
Berechnet man nach der Tabelle das Verhältniß der Höhe der Schützenöffnung zur
Druckhöhe, so ergibt sich Folgendes:
Für Nr. 1 ist dieß
Verhältniß
= 1 : 13 (beinahe).
„ Nr.
2 „ „
„
= 1 : 16 „
„ Nr.
4 „ „
„
= 1 : 24 „
„ Nr.
5 „ „
„
= 1 : 35 „
Man hat also für das erste Verhältniß den Ausflußcoefficienten 0,94, für das zweite
0,93 und für die. folgenden etwa 0,90 zu nehmen. Beträgt z.B. bei einem Gerinne für
einen Hammer die Höhe der Schützenöffnung 5 Zoll, und dieß ist durchschnittlich das
Maximum derselben, die Druckhöhe aber etwa 6 Fuß, so wird der Coefficient 0,94 der
richtigere seyn. Dagegen wird man für eine Druckhöhe von 5 Fuß und eine
Schützenöffnung von 2 bis 3 Zoll 0,90 als den richtigeren Ausflußcoefficienten
annehmen dürfen. U.s.f.
II.
Hiernach wollen wir nun die Wassermenge und die Nutzwirkung der Hammerräder für
einige von den Versuchen berechnen, welche Herr Egen im
Juli 1828 an dem Wagenhammer auf der Müggenbach in der Gemeinde Remscheid angestellt
und die er auf Seite 82 seines oben angeführten Werkes in einer Tabelle
zusammengestellt hat. – Wir lassen dieselbe hier im Auszuge folgen.
Textabbildung Bd. 158, S. 10
Nr. des Versuchs; Schützenöffnung;
Wasserconsumtion; Breite; schräge Höhe; Druckhöhe; pr. Secunde; pr. Schaufel;
Kraftmoment; Zeit eines Radumlaufs; Effectmoment; Nutzeffect; Ganzer Widerstand;
Ganzes Gefälle; Linien; Kubikf.; Fußpfd.; Sec.; Prc.; Pfd.; Zoll.
Unsere Berechnungen beziehen sich auf die Nummern 1, 2, 4, 5, 7 und 10 der
vorstehenden Tabelle. Die Effect-Momente des Rades sind nach den besten
Formeln ermittelt worden, unter Zugrundelegung größerer, nach einem genauen
Transversalmaaßstab angefertigten Zeichnungen. Da es nothwendig ist, daß. man zu
derartigen Berechnungen die Größenverhältnisse des Rades genau kennt, so theilen wir
dieselben hier so mit, wie sie Egen in seinem Werke
aufgeführt hat.
Der Durchmesser des Rades betrug 8,58 Fuß, die Breite desselben im Lichten 3,30 Fuß,
die Tiefe des Radkranzes im Lichten 11,25 Zoll. Das Rad hatte 16 Schaufeln und die
Richtung derselben bildete mit dem Radius an der äußeren Peripherie einen Winkel von
41 Grad. Die senkrechte Höhe der Schußrinne betrug 1,75 Fuß, sie war unter einem
Winkel von 28 1/5 Grad gegen den Horizont geneigt.
Nr. 1.
Nr. 2.
Nr. 4.
Nr. 5.
Nr. 7.
Nr. 10.
Senkrechte Höhe der Schützenöffnung
0,1437 Fuß
0,207 Fuß
0,1241 Fuß
0,183 Fuß
0,137 Fuß
0,229 Fuß
Breite derselben
2,1215 Fuß
2,1215 Fuß
2,1215 Fuß
2,1215 Fuß
2,1215 Fuß
2,1215 Fuß
Inhalt derselben
0,3046 Qdrtf.
0,4388 Qdrtf.
0,2631 Qdrtf.
0,388 Qdrtf.
0,290 Qdrtf.
0,485 Qdrtf.
Druckhöhe
4,125 Fuß
4,09 Fuß
3,687 Fuß
3,653 Fuß
5,319 Fuß
5,18 Fuß
Theoretische Ausflußmenge
4,88 Kbkf.
7,01 Kbkf.
3,99 Kbkf.
5,857 Kbkf.
5,28 Kbkf.
8,72 Kbkf.
Ausflußcoefficient
0,90
0,92
0,90
0,92
0,90
0,90
Wirkliche Ausflußmenge
4,39 Kbkf.
6,45 Kbkf.
3,59 Kbkf.
5,38 Kbkf.
4,76 Kbkf.
7,85 Kbkf.
Eintrittsgeschwindigk. des Wassers bei
3 bis 5 Proc. Verlust auf der
Schußrinne
18,7 Fuß
18,57 Fuß
17,97 Fuß
17,84 Fuß
20,40 Fuß
19,01 Fuß
Zeit eines Radumlaufs
3,59 Sec.
2,61 Sec.
4,46 Sec.
3 Sec.
3,47 Sec.
3,22 Sec.
Geschwindigk. des Rades an der
Stelle wo das Wasser die Schaufeln
trifft
7 Fuß
9,62 Fuß
5,63 Fuß
8,37 Fuß
7,24 Fuß
7,8 Fuß
Wirkung durch den Stoß
751,5 Fpfd. (a)
1142,7 Fpfd. (a)
517,3 Fpfd. (a)
879,5 Fpfd. (a)
940,0 Fpfd. (a)
1417,3 Fpfd. (a)
Höhe des Ausgußbogens (nach
der Zeichnung gemessen)
2,62 Fuß
4,00 Fuß
2,73 Fuß
3,26 Fuß
3,0 Fuß
4,42 Fuß
Wirkung im Ausgußbogen
389,4 Fpfd. (b)
714,8 Fpfd. (b)
305,5 Fpfd. (b)
504,0 Fpfd. (b)
366,4 Fpfd. (b)
1052,0 Fpfd. (b)
Höhe des darüber liegenden
Bogens (gemessen)
2,80 Fuß
1,23 Fuß
3,10 Fuß
2,13 Fuß
2,61 Fuß
1,01 Fuß
Wirkung in demselben
811,1 Fpfd. (c)
523,4 Fpfd. (c)
734,5 Fpfd. (c)
756,4 Fpfd. (c)
816,4 Fpfd. (c)
523,0 Fpfd. (c)
––––––––––––––
––––––––––––––
––––––––––––––
––––––––––––––
––––––––––––––
––––––––––––––
Effect-Moment oder Totalleistung
1952,0 Fpfd. = (a + b + c)
2380,9 Fpfd. = (a + b + c)
1557,3 Fpfd. = (a + b + c)
2139,9 Fpfd. = (a + b + c)
2122,8 Fpfd. = (a + b + c)
2992,3 Fpfd. = (a + b + c)
Der Versuch mit dem Dynamomet. gab:
1917,1 Fpfd.
2636,9 Fpfd.
1541,8 Fpfd.
2292,9 Fpfd.
1982,0 Fpfd.
2985,4 Fpfd.
––––––––––––––
––––––––––––––
––––––––––––––
––––––––––––––
––––––––––––––
––––––––––––––
Differenz
+ 34,9 Fpfd.
– 256,0 Fpfd.
+ 15,5 Fpfd.
– 153,0 Fpfd.
+ 140,8 Fpfd.
+ 6,9 Fpfd.
Da bei der letzten Berechnung (Nr. 10) die Höhe der Schützenöffnung am größten war,
so hätte man hier auch 0,92 oder sogar 0,93 als Ausflußcoefficienten nehmen müssen.
Dann würde aber freilich die berechnete Wirkung des Rades mit der beobachteten
weniger genau übereingestimmt haben, als dieß in der Tafel geschehen ist, indessen
kann auch eine solche Uebereinstimmung nur eine zufällige seyn.
Der Unterschied der beobachteten und berechneten Leistung des Rades beträgt in Nr. 2
stark – 9, in Nr. 5 beinahe – 7 und in Nr. 7 stark + 7 Proc. von der
ersteren. Diese Unterschiede sind natürlich theils den Beobachtungsfehlern mit dem
Dynamometer u.a., theils den mehr oder weniger ungenauen Zahlen, welche in derartige
Rechnungen eingeführt werden müssen, zuzuschreiben. Da die ersteren bis zu 5 Proc.
und die durch Rechnung entstandenen mindestens ebensoviel betragen können, so kann
sich möglicherweise zwischen beiden ein Unterschied von 10 Proc. ergeben. Diese
Differenz hat sich in Nr. 2 beinahe herausgestellt. Uebrigens beweisen die
erhaltenen Effect-Momente wohl unzweideutig, daß die Ausflußcoefficienten,
welche wir den Berechnungen unterlegt haben, als die richtigeren angesehen werden
können, da Beobachtung und Rechnung noch nicht um 10 Proc. von einander
abweichen.
Als die Höhe der beiden wasserhaltenden Bogen des Rades – des obern, in
welchem noch keine Entleerung stattfindet, und des untern, in welchem das Ausgießen
der Zellen erfolgt – nach den trigonometrischen Formeln berechnet wurde,
welche Hr. Professor Weisbach in dem II. Theile seiner
Ingenieur- und Maschinen-Mechanik entwickelt, ergaben sich folgende
Werthe für die Totalleistung des Rades:
Für:
Nr. 1.
Nr. 2.
Nr. 4.
Nr. 5.
Nr. 7.
Nr. 10.
Fußpfund.
1969,1.
2539,2.
1605.
2147,3.
2218.
2987,4.
Hier findet sich allerdings in Nr. 7 eine Abweichung von beinahe 12 Proc. gegen die
Beobachtung; die übrigen Resultate stimmen indessen sehr gut überein.
Wir wollen nun aus den berechneten Werthen und denen der Beobachtung das Mittel
nehmen und darnach die Nutzleistung des Rades für unsere sechs Fälle ermitteln.
Wirkungen des Rades
für:
Nr. 1.
Nr. 2.
Nr. 4.
Nr. 5.
Nr. 7.
Nr. 10.
1952,0
2380,9
1557,3
2139,9
2122,8
2992,7
1969,1
2539,2
1605,0
2147,3
2218,0
2987,4
1917,1
2636,9
1541,8
2292,9
1982,0
2985,4
–––––––––––––––––––––––––––––––––––––––––
Mittel:
1946,1
2519,0
1568,0
2193,3
2107,6
2988,5
Die Gefälle betrugen nach der Tabelle S. 10
für:
Nr. 1.
Nr. 2.
Nr. 4.
Nr. 5.
Nr. 7.
Nr. 10.
178'' = 14',8.
178'' = 14',8.
173'' = 14',4.
173'' = 14',4.
191'' = 16'.
190'' = 15',8.
Demnach das Kraftmoment
für:
Nr. 1.
Nr. 3.
Nr. 4.
Nr. 5.
Nr. 7.
Nr. 10.
Fußpfund.
4354.
6300.
3412.
5111.
4963.
8179.
Dividiren wir diese Zahlen in die obigen für die mittleren Wirkungen des Rades
erhaltenen, so ergibt sich der Nutzeffect für:
Nr. 1.
Nr. 2.
Nr. 4.
Nr. 5.
Nr. 7.
Nr. 10.
= 45 Proc.
= 40 Proc.
= 46 Proc.
= 43 Proc.
= 41 Proc.
= 37 Proc.
(beinahe)
(beinahe)
(beinahe)
(beinahe)
(stark)
(beinahe)
Vergleicht man diese Werthe mit denen auf Seite 10, so stellt sich ein Unterschied
von 12 bis 15 Procent heraus, um welchen die ersteren größer sind, als die
letzteren. Nr. 4 gibt von allen die größte Nutzleistung; dieß läßt sich aber auch
schon von vornherein erkennen, da hier am wenigsten Wasser auf das Rad geschlagen
wird, da dasselbe die kleinste Geschwindigkeit besitzt und die Höhe des
wasserhaltenden Bogens am größten ist.
Aus alle dem geht nun hervor, daß die oben erhaltenen Nutzeffecte als die größten für
Hammerräder nach hiesiger Construction zu betrachten sind. Sie beziehen sich auf die
Fälle, wo das Rad eine mittlere Geschwindigkeit von 7 bis beinahe 10 Fuß besitzt, wo
also die Dauer einer Umdrehung zwischen 2,6 und 3,6 Secunden schwankt und der
Hammer, wenn 10 Daumen in der Welle vorhanden sind, wie dieß bei dem untersuchten
Hammer der Fall war, in der Minute 180 bis 230 Schläge macht. Diese Zahl kann für
Stahlraffinirhämmer, insbesondere auch für Sägenbreithämmer, als eine kleine
betrachtet werden, die nur selten beim Betriebe vorkommt. (Die Breithämmer für
Sensen machen etwa 200 bis 230 Schläge in der Minute.) Bei einer Druckhöhe von 3'
8'', einer Schützenöffnung von 5'' 3''' Höhe und 2' 2'' Weite, machen die hiesigen
Stahlraffinirhämmer nach den Beobachtungen des Verfassers 380 Schläge pro Minute und wenn die Welle 10 Daumen enthält. Dieß
ist denn auch die Zahl, welche beim vollen Gange des Hammers erreicht wird, wenn
unter demselben die weißglühenden Stahlschienen zu einem Stücke zusammengeschweißt
werden, welche Operation etwa die Hälfte der Betriebszeit in Anspruch nimmt. Das Rad
besitzt alsdann eine solche Geschwindigkeit, daß durch die erzeugte, ungeheure
Centrifugalkraft das Wasser nicht vollständig in die Zellen eintreten kann, und
mindestens 2/3 der Gesammtwirkung des Wassers in der Stoßwirkung besteht. In Nr. 3
der Tabelle Seite 10 wurde diese Geschwindigkeit beinahe erreicht. Das Rad machte
in 1,82 Secunden
eine, also in 60 Secunden gleich einer Minute 33 Umdrehungen, die Anzahl der Schläge
betrug demnach 330. Es scheint mir aber, als sey hier die Bremsung des Dynamometers
etwas zu stark gewesen, da die Hämmer bei dieser Druckhöhe und Schützenöffnung 350
bis 360 Schläge pro Minute machen. Demnach muß auch der
Nutzeffect des Rades bei diesem Versuche größer ausgefallen seyn, als er beim
Betriebe des Hammers ausgefallen seyn würde. In der Tabelle ist er für den
Ausflußcoefficienten 0,72 zu 44 Proc. berechnet und mit Zugrundelegung unseres
Ausflußcoefficienten würde derselbe also 32 oder 29 Proc. betragen, da nach unseren
Berechnungen der Nutzeffect um 12 bis 15 Proc. kleiner genommen werden muß, als ihn
Egen berechnet hat. Von diesen 32 oder 29 Proc. sind
aber noch etwa 2 bis 3 Proc. abzuziehen, da die Bremsung etwas zu stark war. Wir
dürfen hieraus schließen, daß diese Räder bei 350 bis 360 Schlägen in der Minute
einen Nutzeffect von 27 bis 29 Proc. geben, daß derselbe aber beim vollen Gange, wo
380 bis 400 Schläge in der Minute gemacht werden, jedenfalls bis auf 25 Proc.
heruntersinkt.
Aus dem Gesagten erhellet nun, daß die hiesigen Hammerräder bei einer mittleren
Geschwindigkeit von 7 Fuß eine Nutzwirkung von etwa 46 Proc. geben, die vielleicht
in einzelnen Fällen auf 50 Proc. steigt, und daß dieselbe bei vollem Gange etwa 25
Proc., selten aber mehr beträgt.
(Der Schluß folgt im nächsten Heft.)
Tafeln