| Titel: | Pyrometrischer Apparat; von C. Schinz. |
| Autor: | C. Schinz |
| Fundstelle: | Band 163, Jahrgang 1862, Nr. LXXXI., S. 321 |
| Download: | XML |
LXXXI.
Pyrometrischer Apparat; von C. Schinz.
Mit Abbildungen auf Tab.
V.
Schinz's pyrometrischer Apparat.
Unter den Anwendungen der Wärme-Meßkunst sind diejenigen die ökonomisch
wichtigsten, welche sich auf sehr hohe Temperaturen beziehen. Das Studium und die
Vervollkommnung derselben sind aber sehr gehemmt durch den Mangel eines geeigneten
Pyrometers.
Diesem Mangel abzuhelfen, war daher seit Jahren mein eifrigstes Bestreben, und die
folgende Mittheilung ist das Resultat, zu welchem mich meine Bemühungen geführt
haben.
Ueber das Pyrometer von Wedgwood ist es Wohl nicht nöthig
eine Kritik anzustellen.
Diejenigen Pyrometer, welche auf der Ausdehnung fester Körper beruhen, sind für sehr
hohe Temperaturgrade ganz unbrauchbar, weil einerseits der
Ausdehnungs-Coefficient bei zunehmender Temperatur nach einem unbekannten
Gesetze wächst, und andererseits die Abkühlung in dem Momente, wo man den Körper aus
dem Ofen entfernt, im Verhältniß zu der absorbirten Wärme außerordentlich groß
ist.
Ganz dieselben Ursachen stehen der Anwendung der pyrometrischen Methode entgegen,
welche sich auf die specifische Wärme stützt.
Die photometrische Methode entbehrt der Kenntniß des Gesetzes, welches das Verhältniß
zwischen Temperatur und Lichtstärke festsetzt.
Das Verfahren, die Temperatur durch schmelzende Metalle oder Legirungen zu bestimmen,
gibt unter den bisher erwähnten Methoden die besten Anhaltspunkte; wenn man aber
bedenkt, daß selbst die Schmelzpunkte der einfachen Metalle noch nicht mit
Sicherheit bestimmt sind, und daß die Schmelzpunkte von Legirungen keineswegs dem
berechneten mittleren Schmelzpunkte ihrer Bestandtheile entsprechen, so muß
zugestanden werden, daß auch diese Bestimmungsart unmöglich zuverlässige, in
Thermometergraden ausdrückbare Resultate zu geben vermag.
Die Wärme-Leitungsfähigkeit der Metalle zum Messen hoher Temperaturen zu
benutzen, ist deßhalb unzulässig, weil der Contact mit derzu messenden Wärmequelle
unmöglich gleichförmig gemacht werden kann, und überdieß die Abkühlung in dem der
Wärmequelle zugekehrten Stücke von der benachbarten Ofenwand mehr oder weniger
beeinflußt wird.
Das thermoelektrische Pyrometer von Pouillet ist wohl nur
für Temperaturen anwendbar, bei welchen das den einen Bestandtheil der Säule
bildende Eisen seinen Aggregatzustand nicht ändert.
Das Luftpyrometer von Regnault
Polytechn. Journal Bd. CLXII S. 361. ist das einzige Instrument, welches unter Anwendung sehr vieler
Vorsichtsmaßregeln und in den Händen eines geschickten Experimentators zuverlässige
und in Thermometergraden ausdrückbare Resultate zu geben vermag.
Diese Eigenschaft verliert aber das Instrument, sobald dasselbe in der Praxis
außerhalb dem Laboratorium benutzt werden soll, da vor einem großen heißen Ofen und
in unmittelbarer Nähe desselben die erforderlichen Vorsichtsmaßregeln unanwendbar
sind; es wären dazu wenigstens sehr complicirte Vorrichtungen und eine große
Geschicklichkeit erforderlich, weßhalb dieses Instrument dem Praktiker nicht zusagen
würde.
Um häufige Beobachtungen anstellen zu können, ist ein Apparat nöthig, welcher leicht
gehandhabt und schnell und mühelos in Function gesetzt werden kann, überdieß keine
gar zu große Geschicklichkeit beansprucht.
Dieser Anforderung wird am besten genügt, wenn man die
Leitungsfähigkeit der Ofenwand als pyrometrisches Mittel benutzt. Es ist
dann nur nothwendig, die Temperatur der äußeren Wandfläche genau zu bestimmen, um
daraus die Temperatur der inneren Fläche durch einfache Rechnung zu erhalten, da
diese beiden Temperaturen nothwendig in einem gewissen Verhältnisse zu einander
stehen.
Hierzu ist es erforderlich, einerseits die Leitungsfähigkeit
der Wand zu kennen, und andererseits die Mittel zu haben, durch welche sich die
Temperatur der äußeren Fläche genau bestimmen läßt.
Denken wir uns eine hohle Kugel, deren Wände eine gewisse Dicke haben, und welche aus
der Substanz besteht, deren Leitungsfähigkeit man prüfen will; der hohle Raum im
Innern dieser Kugel sey mit warmem Wasser von bekannter Temperatur und bekanntem
Gewicht gefüllt, und dann die Kugel in ein bekanntes Gewicht von kaltem Wasser
getaucht, so wird das warme Wasser im Innern der Kugel zuerst Wärme an die Substanz
abgeben, aus der die Kugel besteht, und dann wird die Wärme durch diese
hindurchgehen und das kalte Wasser dieselbe aufnehmen.
Hätte das heiße Wasser das Gewicht 10 Pfd. (5 Kilogr.) gehabt, und wäre dessen Temperatur
80° C. gewesen, hätte das kalte Wasser 40 Pfd. gewogen und 10° gehabt,
und hätte nach einiger Zeit das Wasser in der Kugel 75° und das Wasser
außerhalb 11°, so hat ersteres 50 Wärmeeinheiten verloren und letzteres 40 W.
E. aufgenommen, und es sind also in dieser Zeit 40 W. E. durch die Kugel gegangen
und 10 W. E. von derselben absorbirt worden.
Angenommen, die Zeit in welcher diese 40 W. E. durchgegangen sind, habe 126 Secunden
betragen, so ist die Transmission per Stunde = (3600 .
40)/126 = 1143 W. E. gewesen.
Es habe ferner die Kugel eine Oberfläche von 2,3 Quadratfuß gehabt, so ist die per Stunde und per
Quadratfuß durchgegangene Wärmemenge = 1143/2,3 = 497 W. E.
Hätte endlich die Kugel 0,2 Fuß Wanddicke = e gehabt, so
würde die Transmission für eine 1 Fuß dicke Wand = 497 . 0,2 = 99,4 W. E.
betragen.
Nun ist noch zu bestimmen, bei welcher Temperatur-Differenz zwischen der
inneren und der äußeren Kugelwand, diese Transmission stattgefunden hat.
Nachdem die Wand die ihr zuströmende Wärme absorbirt hatte, war die Temperatur des
Wassers in der Kugel noch 79°, und am Ende des Versuchs 75°, daher die
mittlere Temperatur desselben = t = (79 + 75)/2 =
77°.
Die Temperatur des Wassers, welches die Kugel umgab, war anfangs 10°, und nach
dem Versuche 11°, daher dessen mittlere Temperatur = t'' = (10 + 11)/2 10°,5.
Erfahrungsgemäß transmittirt 1 (metrischer) Quadratfuß Fläche an Wasser per Stunde 778 W. E. = Q,
wenn diese Fläche eine Temperatur hat, die um 1° höher ist als diejenige des
sie berührenden Wassers. Daher ist die Temperatur der Kugelwand 497/778 =
10°,5 = t' = 11°,14 gewesen.
Wir haben somit:
Q
= Transmissions-Coefficient für Wasser
= 778 W. W.
e
= Wanddicke
= 0,2 Fuß.
t
= Temperatur der inneren Wandfläche
= 77°.
t'
=
„ der
äußeren „
= 11°,14.
t''
=
„ des
Wassers außer der Kugel
= 10°,5.
Die Leitungsfähigkeit des Materials, woraus die Kugel besteht = C, per Stunde pro 1 Quadratfuß – für
die Wanddicke 1 Fuß und für 1° Temperatur-Differenz zwischen der
inneren und äußeren Wandfläche – bestimmt, wird in Wärmeeinheiten
ausgedrückt, und ist:
Textabbildung Bd. 163, S. 324
in unserem Falle
Textabbildung Bd. 163, S. 324
Ist einmal C bekannt und t'
und t'', so können wir t
bestimmen durch:
Textabbildung Bd. 163, S. 324
Ebenso läßt sich t' bestimmen durch:
Textabbildung Bd. 163, S. 324
Im Vorhergehenden ist im Allgemeinen eine der Methoden angegeben, durch welche die
Leitungsfähigkeit verschiedener Körper bestimmt werden kann, und es ist nicht nöthig
genauere Angaben über diese Methode zu geben, da wir dieselbe nicht ferner in
Anwendung bringen, weil es nicht nur sehr schwierig, sondern sogar unmöglich seyn
würde, alle auf ihre Leitungsfähigkeit zu untersuchenden Materialien in die Form von
gleichförmig dicken hohlen Kugeln zu bringen. Sonst muß allerdings anerkannt werden,
daß diese Methode die natürlichste ist, da nicht nur das Wasser als wärmeaufnehmende
Flüssigkeit große Genauigkeit in der Beobachtung zuläßt, sondern auch die
transmittirende Wärme der ganzen Fläche in Rechnung kommt.
Da, wie die vorstehenden Formeln zeigen, die Leitungsfähigkeit aus t, t', und t'' bestimmt
werden kann, so kann auch eine andere Methode angewandt werden, wobei diese
letzteren drei Werthe durch Beobachtung erhoben werden. Nur ist es dann nöthig, daß
die Transmission der Wärme durch die zu prüfende Substanz hindurch – anstatt
an Wasser, an Luft – stattfinde, wodurch dann der Werth von Q ein mit der Temperatur-Differenz wechselnder
wird.
Dieses Verfahren besteht im Allgemeinen darin, daß man eine thermoelektrische Säule
zwischen zwei Flächen bringt, von denen die eine durch den von einer Seite mit Dampf
geheizten zu untersuchenden Körper gebildet ist, die andere aber aus einem mit
Wasser gefüllten dünnen Metallgefäße besteht, dessen Temperatur willkürlich
verändert werden kann, bis das mit der Säule verbundene Rheometer auf 0 steht und dadurch anzeigt, daß
die zugekehrten Flächen von einerlei Temperatur sind. Da nun die Temperatur des
Wassers direct durch das Thermometer angegeben werden kann, die Temperatur der
anderen Fläche aber dieselbe ist, so erhält man dadurch den Werth von t'.
Die Werthe von Q sind dann nach der Formel von Dulong:
Q = S m a
t'' (a
t0 – 1) + Lnt
0b
zu berechnen, in welcher t''
dieselbe Bedeutung hat wie oben, t⁰ die
Temperatur-Differenz der transmittirenden Fläche gegen diejenige der Luft
bezeichnet, S den Strahlungs-Coefficienten der
Fläche, und L den Transmissions-Coefficienten für
die Luft. a ist = 1,0077; m
und n sind zwei Constante.
Da die Wärme-Transmission sich auf l⁰
Temperatur-Differenz = t' – t'' = t⁰ bezieht, so
ist obige Formel noch durch t⁰ zu dividiren, und
wir erhalten:
Q = (S m
a
t'' (a
t0 – 1) + Lnt
0b)/t⁰
Die Werthe von S und L sind
nach der Natur der wärmeausstrahlenden Fläche und nach der Höhe derselben zu
bestimmen.
Die Werthe für S sind:
0,7218 für Kienruß,
0,6786 für Papier,
0,6678 für Oelfarbe-Anstrich.
Damit beide Flächen gleiche Temperatur anzeigen, ist nothwendig, daß beide gleiche
Strahlung haben; zu diesem Ende hat Peclet beide Flächen
mit Papier überzogen, ich habe es aber bequemer gefunden, sie mit Oelfarbe
anzustreichen, da Papier an manchen Flächen nicht leicht haftet.
Der Transmissions-Coefficient L wechselt mit der
Höhe der sich abkühlenden Fläche; da die Luft, indem sie unten an die verticale
Fläche antritt, sogleich Wärme aufnimmt und dann an der Fläche emporsteigt, und je
höher sie heraufkommt, eine immer kleiner werdende Temperatur-Differenz hat,
so ist die Transmission an den höher gelegenen Stellen kleiner, an den tiefer
gelegenen Stellen größer; der Werth von L muß also die
mittlere Transmission bestimmen, und ist:
L = 0,3175 + 0,209/√h
worin h die Höhe der Fläche in
Fußen ausdrückt.
Ist nun h = 0,3', so wird der Werth von L = 0,7054.
Die Werthe von Q für t₀ = t' – t'' = 30° bis 249° habe ich in folgender Tabelle
zusammengestellt, vermittelst welcher die Beobachtungsresultate mit dem nun zu
beschreibenden Apparate zu berechnen sind.
Werthe von Q
zur Bestimmung der Leitungsfähigkeit verschiedener Körper.
Werth von S
= 0,6678 für Oelfarbe-Anstrich.
„
von L
= 0,7054 für Platten von 9 Centimeter = 3'' Höhe.
Werthe
von:
t₀
Q
t₀
Q
t₀
Q
5°
1,3238
45°
1,83221
85°
2,1438
6
1,3568
46
1,84051
86
2,1513
7
1,3800
47
1,84877
87
2,1587
8
1,4030
48
1,85746
88
2,1662
9
1,4222
49
1,86487
89
2,1738
10
1,4416
50
1,87348
90
2,1813
11
1,4592
51
1,88094
91
2,1889
12
1,4761
52
1,89004
92
2,1967
13
1,4916
53
1,89810
93
2,2038
14
1,5068
54
1,90832
94
2,2113
15
1,5215
55
1,91421
95
2,2187
16
1,5353
56
1,92212
96
2,2264
17
1,5488
57
1,93000
97
2,2337
18
1,5620
58
1,93801
98
2,2439
19
1,5745
59
1,94585
99
2,2488
20
1,5867
60
1,95371
100
2,2564
21
1,5989
61
1,96153
101
2,2640
22
1,6104
62
1,96893
102
2,2714
23
1,6221
63
1,97696
103
2,2790
24
1,6330
64
1,98467
104
2,2868
25
1,6441
65
1,99246
105
2,2942
26
1,6551
66
1,99872
106
2,3017
27
1,6652
67
2,00780
107
2,3093
28
1,6757
68
2,01460
108
2,3160
29
1,6857
69
2,02320
109
2,3245
30
1,69514
70
2,0307
110
2,3321
31
1,70554
71
2,0385
111
2,3398
32
1,71541
72
2,0437
112
2,3475
33
1,72488
73
2,0534
113
2,3549
34
1,73231
74
2,0610
114
2,3627
35
1,74650
75
2,0687
115
2,3701
36
1,75306
76
2,0766
116
2,3782
37
1,76236
77
2,0837
117
2,3860
38
1,77130
78
2,0917
118
2,3936
39
1,78021
79
2,0988
119
2,4024
40
1,78909
80
2,1052
120
2,4091
41
1,79775
81
2,1112
121
2,4170
42
1,80658
82
2,1193
122
2,4247
43
1,81517
83
2,1288
123
2,4325
44
1,82391
84
2,1373
124
2,4402
Werthe von:
t₀
Q
t₀
Q
t₀
Q
125°
2,4482
174°
2,8611
223°
3,3570
126
2,4559
175
2,8702
224
3,3693
127
2,4669
176
2,8794
225
3,3795
128
2,4746
177
2,8887
226
3,3909
129
2,4797
178
2,8979
227
3,4023
130
2,4880
179
2,9073
228
3,4139
131
2,4958
180
2,9166
229
3,4254
132
2,5035
181
2,9231
230
3,4368
133
2,5116
182
2,9353
231
3,4486
134
2,5197
183
2,9448
232
3,4602
135
2,5288
184
2,9542
233
3,4719
136
2,5357
185
2,9637
234
3,4837
137
2,5438
186
2,9746
235
3,4956
138
2,5519
187
2,9831
236
3,5074
139
2,5568
188
3,9926
237
3,5191
140
2,5683
189
3,0020
238
3,5316
141
2,5757
190
3,0120
239
3,5436
142
2,5844
191
3,0218
240
3,5558
143
2,5927
192
3,0316
241
3,5681
144
2,6010
193
3,0413
242
3,5805
145
2,6092
194
3,0512
243
3,5926
146
2,6175
195
3,0612
244
3,6051
147
2,6258
196
3,0715
245
3,6173
148
2,6342
197
3,0811
246
3,6299
149
2,6398
198
3,0911
247
3,6423
150
2,6510
199
3,1051
248
3,6552
151
2,6593
200
3,1113
249
3,6679
152
2,6677
201
3,1215
250
3,6806
153
2,6757
202
3,1317
251
3,6936
154
2,6847
203
3,1420
252
3,7063
155
2,6933
204
3,1533
253
3,7192
156
2,7052
205
3,1627
254
3,7318
157
2,7102
206
3,1702
255
3,7453
158
2,7179
207
3,1835
256
3,7584
159
2,7277
208
3,1940
257
3,7716
160
2,7363
209
3,2045
258
3,7849
161
2,7457
210
3,2164
259
3,7986
162
2,7552
211
3,2257
260
3,8117
163
2,7621
212
3,2367
261
3,8251
164
2,7713
213
3,2471
262
3,8387
165
2,7803
214
3,2568
263
3,8522
166
2,7876
215
3,2687
264
3,8660
167
2,7980
216
3,2789
265
3,8797
168
2,8104
217
3,2903
266
3,8938
169
2,8173
218
3,3063
267
3,9074
170
2,8247
219
3,3124
268
3,9213
171
2,8339
220
3,3235
269
3,9351
172
2,8428
221
3,3345
173
2,8519
222
3,3457
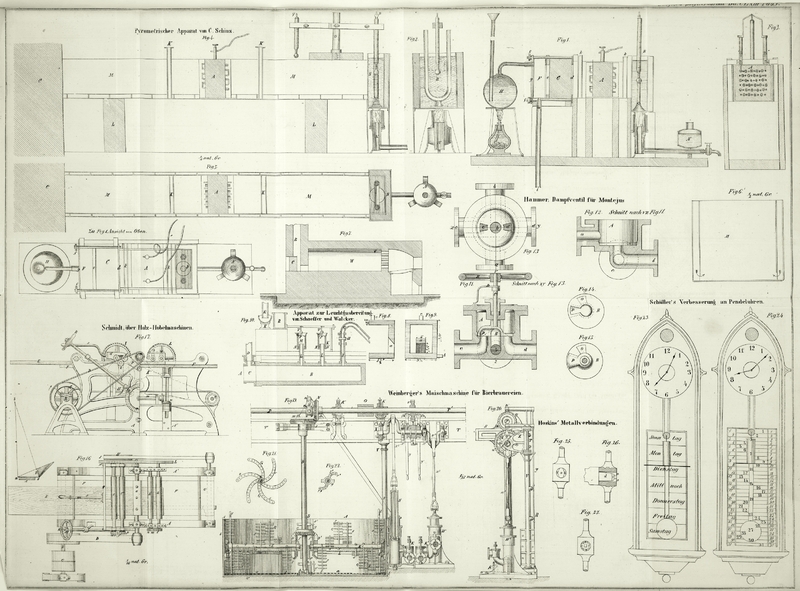
Apparat zur Bestimmung der Leitungsfähigkeit des Materials der
Ofenwand. – Fig. 1 zeigt denselben im
Längendurchschnitt.
A ist die thermoelektrische Säule; B ein Wassergefäß mit darunter gestellter
Weingeistlampe; C ein quadratisches Stück des zu
prüfenden Materials; d eine quadratisch ausgeschnittene
Eisenblechscheibe, an der vier Schrauben befestigt sind, die das Stück C gegen eine ebenfalls ausgeschnittene Kautschukscheibe
e und gegen das Blechgefäß F drücken, indem die Schraubenmuttern f, f
über der Platte g, g fest angezogen werden. H ist ein kleiner kugelförmiger Dampfkessel mit darunter
gestellter Weingeistlampe. Der Dampf wird in das Gefäß F
geleitet, und kommt so mit der Rückseite des Körpers C
in Berührung. Das condensirte Wasser wird durch die kleine Röhre i abgeleitet.
Die thermoelektrische Säule A ist mit einem Rheometer,
welches in der Figur nicht sichtbar ist, in leitender Berührung.
k, k sind zweiwandige hohle Schieber, durch welche die
Luft strömen kann; dieselben werden im Momente der Beobachtung weggehoben.
Fig. 2 zeigt
einen transversalen Durchschnitt durch das Wassergefäß B, mit dem darin eingetauchten genauen Thermometer.
Fig. 3 ist ein
Durchschnitt der thermoelektrischen Säule, wie dieselbe in der, der Luftströmung
Spielraum gebenden Doppelrinne liegt. Die Säule besteht aus 30 runden Wismuthstäben
von 5 Millimetern Durchmesser und 70 Millimet. Länge, und aus 30 Kupferdrähten von 2
Millim. Durchmesser von gleicher Länge. Dieselben sind durch Carton und Siegellack
von einander isolirt, und die gelötheten Enden ragen 5 Millimeter aus dieser
Einbettung hervor. Das Ganze ist in eine Blechumhüllung eingeschlossen.
Was die Platte des zu prüfenden Materiales C anbetrifft,
so ist dieselbe im senkrechten Querschnitte quadratisch, und für einen und denselben
Apparat immer von gleichen Dimensionen zu machen, die Dicke derselben kann wechseln;
ist das Material ein sehr stark leitendes, so ist es gut derselben 2 Zoll Dicke zu
geben, bei geringerer Leitungsfähigkeit kann auch 1 Zoll Dicke genügen. Die dem
Dampfe zugekehrte Fläche muß, wenn das Material porös ist, mit einem Ueberzuge
versehen werden, der das Eindringen des Dampfes verhindert. In den meisten Fällen
genügt dazu ein zweimaliger Anstrich mit Oelfarbe. Ist die zu prüfende Substanz
pulverförmig, so dient ein oben offenes Blechgefäß, welches die Form und Größe der
Platten hat und statt dieser vor dem Dampfgefäße F
befestigt wird. Damit das zu prüfende Material vollkommen mit der Wärme, die dem
Dampfe zukommt, gesättigt sey, ist es nothwendig denselben1, 2 bis 3 Stunden auf die
Platte einwirken zu lassen, ehe man zu einer Bestimmung schreitet. Um zu erproben ob
die Platte mit Wärme gesättigt sey, öffnet man jede halbe Stunde den Schieber k, welcher vor der Platte steht, und beobachtet die Zahl
der Grade, welche das Rheometer gibt; ist diese Zahl bei zwei sich folgenden
Beobachtungen gleich, so ist dieß ein Beweis daß die Platte entsprechend gesättigt
ist.
Bei Beobachtung der Multiplicatornadel muß man die Wärme 1 bis 2 Minuten lang auf die
Säule wirken lassen, damit sie stationär wird; nachdem der Schieber k wieder eingesetzt ist, geht die Multiplicatornadel nur
langsam zurück, weil die Säule eine gewisse Menge von Wärme absorbirt hat, die nun
wieder zerstreut werden muß. Es ist daher sehr zu empfehlen, den Schieber nie länger
offen zu lassen, als durchaus nothwendig ist um die Beobachtung machen zu können, 2
Min. reichen gewöhnlich dazu aus. Bei jeder Beobachtung ist die Nadel des
Multiplicators in Schwingung zu bringen, was durch Annäherung eines kleinen
Magnetstabes leicht zu bewerkstelligen ist; der Zweck dieses Kunstgriffes ist die
Trägheit zu überwinden, welche sie dem Strom entgegensetzt.
Diese Vorsicht wäre nicht nur überflüssig, sondern sogar unbequem, wenn das Rheometer
von gewöhnlicher Einrichtung wäre, wobei die astatischen Nadeln an einem Coconfaden
hängen; ein so empfindliches Instrument ist im Laboratorium und von geschickten
Händen zu gebrauchen, aber in der Hütte und in der nächsten Nähe der auf ihre
Temperatur zu prüfenden Oefen würde eine Nadel am Coconfaden nur schwer zur Ruhe zu
bringen seyn; außerdem muß das Instrument zu praktischem Gebrauche leicht
transportirbar seyn, und auf keine Weise leicht in Unordnung kommen. Das Rheometer
welches ich daher für diesen Zweck anwende, besteht einfach in einer Dose aus
Messing, die auf drei Stellschrauben ruht, aus 30 Windungen von mit Seide
übersponnenem Kupferdraht von 1 Millimeter Dicke, dann zwei rhombischen Nadeln von
dünnem Stahlblech, die so asiatisch gemacht sind, daß sie sich mit schwacher
Intensität in dem magnetischen Meridian einstellen, und zwar so, daß sie in 6
Secunden nur eine Schwingung machen. Die obere Nadel ist mit Achathütchen versehen,
und läuft auf einer feinen Stahlspitze; die untere Nadel ist durch einen
gabelförmigen Draht an der oberen aufgehängt. Da der thermoelektrische Strom auf die
Nadeln am mächtigsten wirkt, wenn dieselben nur sehr wenig vom magnetischen Meridian
abgelenkt werden, so kann 1/2° des Thermometers durch das Rheometer noch
deutlich angegeben werden, wenn die Säule nicht allzu weit von den erwärmten Flächen
entfernt ist. Dieß ist z.B. der Fall, wenn diese Entfernung nur 5 Centimeter
beträgt; bei 24 Centimeter Entfernunggehen schon 3 Thermometergrade auf 1° des
Rheometers. Es versteht sich, daß die Multiplicatordose mit einer Glasplatte
zugedeckt ist, und daß die Nadeln zum Transport von der Spitze abhebbar gemacht
sind.
Ist nun die zu untersuchende Substanz auf eine constante Temperatur gebracht, so wird
das Wasser im Gefäße B auf eine höhere Temperatur
erwärmt als die Substanz hat; nachdem die Lampe entfernt ist, wird das Wasser
umgerührt, damit es eine gleichförmige Temperatur annehme, die zwar nie gleichförmig
bleibt, aber wenn die Thermometerkugel in der Mitte hängt, so wird doch sehr nahe
die mittlere Temperatur angegeben.
Man zieht nun gleichzeitig beide Schieber k, k; findet
man dabei, daß das Rheometer mehr als 1° von 0 abweicht, so werden die
Schieber sogleich wieder in die Rinne gestellt und von Zeit zu Zeit wieder
weggenommen, bis die Temperatur des Wassers am Rheometer 1° zeigt. Man läßt
nun beide Schieber offen, notirt die Temperatur des Wassers, beobachtet und notirt
dann dessen Temperatur wenn das Rheometer auf 0 steht, und endlich wenn dasselbe um
1° zurückgegangen ist. Das Mittel dieser drei Temperaturen des Wassers kann
mit ziemlicher Sicherheit als die Temperatur angenommen werden, welche der
Oberfläche der zu untersuchenden Substanz zukommt.
Besondere Genauigkeit ist bei der Bestimmung der Dicke der untersuchten Platte
nothwendig, da schon eine Zehntels-Linie eine sehr beträchtliche Differenz im
Rechnungsresultate macht. Sollte die Platte nicht überall völlig gleich dick seyn,
so muß sie durch Schleifen gleich dick gemacht werden.
Dieser Apparat und diese Methode zur Bestimmung der Leitungsfähigkeit verschiedener
Materialien stehen der zuerst beschriebenen Methode nach, insofern die Seitenwände
der Tafeln C Wärme zerstreuen und daher die Temperatur
der Fläche, welche bestimmt werden soll, vermindern; könnte man diese seitliche
Transmission auf irgend eine Weise ganz aufheben, so würde diese Methode jeder
anderen vorzuziehen seyn, da dieß aber nicht möglich ist, so nützt es auch nichts
diese Transmission, wie Peclet gethan hat, durch eine
Umhüllung beschränken zu wollen, weil es ganz gleichgültig ist, ob wir den zur
Correction nöthigen Coefficienten etwas größer oder etwas kleiner nehmen, wenn nur
die Temperatur-Erniedrigung stets der Dicke e und
der Fläche gegen die Säule proportional bleibt, und dieß wird geschehen, wenn die
Platten C stets gleichen Verticalschnitt haben.
Um den für die Correction nothwendigen Coefficienten zu finden, hat Peclet einige Versuche nach der ersten Methode angestellt
und die daraus erhaltenen Bestimmungen mit denjenigen verglichen, welche diezweite Methode mit
demselben Material ergab. Seine mit Holz umhüllten Platten hatten 20 Centimeter Höhe
und Breite, und hierzu stimmte der Coefficient 1,203, welcher mit dem Werthe von Q zu multipliciren ist. Um bei identischem Material
gleiche Resultate mit Peclet zu erhalten, verlangen
unumhüllte Platten von 11 Centimetern Seite den Coefficienten 1,5496. Es versteht
sich von selbst, daß dieser Coefficient ein anderer wird, sobald der senkrechte
Querschnitt der Platten C verändert wird.
Bezeichnen wir diesen Corrections-Coefficienten mit φ, so wird die Formel
Textabbildung Bd. 163, S. 331
Auf diese Weise habe ich eine Reihe von Materialien untersucht, welche zur
Construction von Verbrennungsapparaten angewandt werden, und folgende Resultate
erhalten:
Material.
Dicke der Platten = e
t'
t''
C
Spec. Gewicht.
Tannenholz, parallel den
Fasern
0,137'
32°
15°
0,1020
Feuerfeste
Steine:
von Bellelay, porös
0,137
52
20
0,2428
1,003
dtto.
0,137
56
20
0,3045
1,405
dtto.
0,137
55
20
0,2884
1,000
dtto.
0,143
55
20
0,3790
1,258
von Aschau, porös
0,190
48,5
19
0,2842
1,327
dtto.
0,210
47
17,8
0,3022
1,490
dtto.
gewöhnliche
0,223
44
15
0,3017
1,929
von Deffernick, porös
0,178
51
13,5
0,3730
1,250
dtto.
gewöhnliche
0,183
56
16
0,4612
1,927
von Zell a./H., gewöhnliche
0,183
54
17
0,4020
1,800
von Münster in Nassau
0,183
52,5
15,2
0,3925
1,880
Aschauer Glashafenwand
0,133
60
17
0,4022
1,858
Ordinäre
Backsteine:
von Offenburg
0,166
51,5
15,5
0,3347
1,700
von Basel, durchhält um 30 Proc.
0,213
42
16
0,2449
1,316
Man ersieht aus dieser Tabelle, daß wohl specifisch schwerere Materialien im
Allgemeinen die Wärme mehr leiten als specifisch leichte, daß aber dennoch die
Leitungsfähigkeit auch durch die übrige Natur des Materials modificirt wird.
Die Temperatur der Ofenwand kann nun auf analoge Weise
bestimmt werden, und wenn die Leitungsfähigkeit des Materials derselbenso wie deren Dicke genau
ermittelt sind, daraus die Temperatur des Ofens selbst = t, gefunden werden durch:
Textabbildung Bd. 163, S. 332
Da aber schon bei sehr geringer Leitungsfähigkeit des Materials und 8 Zoll Wanddicke
die Temperatur der Oberfläche meist höher als 100° C. werden wird, so können
wir das Wasser nicht mehr zur thermometrischen Bestimmung brauchen. Wäre z.B. die
Temperatur im Ofen = t = 1887°, die Temperatur
der Luft = t'' = 15°, die Dicke der Wand = e = 0,8', und die Leitungsfähigkeit derselben = C = 0,25, so hätten wir:
Textabbildung Bd. 163, S. 332
Wir müssen daher das Wasser gegen eine Substanz vertauschen, welche höhere
Temperaturen anzuzeigen vermag.
Dazu dient nun Stearinsäure und ein hart gelöthetes Gefäß von Kupfer, welches
übrigens dieselbe Einrichtung haben kann wie das Wassergefäß. Dieselbe
thermoelektrische Säule und dasselbe Rheometer können auch zu dieser Bestimmung
dienen; dagegen kann die Säule nicht so nahe an die warmen Flächen gerückt werden,
wie bei der Bestimmung der Leitungsfähigkeit, weil die große Masse des Ofens in
solcher Nähe störend einwirken würde.
Erinnern wir uns an die Bestimmung des Werthes von L,
welcher einer der Factoren der Wärme-Transmission an Luft ist, so ist leicht
einzusehen, daß der Apparat so angeordnet werden muß, daß die Luftströmung an den
sich gegenüberstehenden Flächen eine gleiche werde.
Dieß ist nun bloß dadurch erreichbar, daß wir die Rinne, worin die Säule liegt, genau
an die Ofenwand anstoßen lassen, und damit von der Ofenwand eine Fläche isoliren,
welche derjenigen des Stearinsäure-Gefäßes gleichkommt. Die Ofenwandfläche
welche über der Rinne hervorragt, ist von keinem Einflusse mehr auf die Temperatur
desjenigen Stücks Ofenwand, welches von der Rinne eingeschlossen wird; wohl aber
kann die strahlende Wärme, welche von derselben ausgeht, auf die Säule wirken, daher
diese höher gelegenen Theile der Ofenwand durch einen Schirm zu schützen sind, der
die strahlende Wärme vom Apparate abhält.
Die Genauigkeit der Bestimmung der Ofentemperatur hängt nun von der Leitungsfähigkeit
und Dicke der Wand ab, an welcher die Messung vorgenommen wird.
Nehmen wir als Dicke = e = 8 Zoll, und für die
Leitungsfähigkeitsuccessive 0,4; 0,3; 0,2 und 0,1, so wird die zu beobachtende äußere Temperatur
der Wand = t' bei t'' =
15° und t = 1800°
Textabbildung Bd. 163, S. 333
Es kämen also auf je 1° innerer Ofen-Temperatur = t je
7,6°
;
8,8°
;
11,0°
; 17,0°
Wand-Temperatur = t',
woraus folgt, daß genauere Resultate mit einer besser leitenden, oder, was auf
dasselbe hinauskommt, mit einer weniger dicken Wand erhalten werden.
Apparat zur Bestimmung der Temperatur der Ofenwand.
– Fig.
4 stellt denselben im Längendurchschnitt dar, Fig. 5 im horizontalen
Durchschnitte. A ist die thermoelektrische Säule, B das Stearinsäure-Gefäß;
C ist ein Stück der Ofenwand, welches, so weit es von der Rinne eingefaßt
wird, mit Oelfarbe angestrichen ist, insoferne die der Säule zugekehrte Fläche des
Gefäßes B einen solchen Ueberzug hat. K, K sind zwei Schieber, wie die früher beschriebenen.
L, L sind zwei Holzklötze zur Unterstützung der
Rinne M, M. N ist die Weingeistlampe unter dem
Stearinsäure-Gefäß B. O ist ein Ständer, welcher
über die Rinne gestellt wird; er ist mit zwei Zargen versehen, in welche die
Thermometer p und q
eingeklemmt sind. Die Kugel des Thermometers p ragt in
die Mitte der geschmolzenen Stearinsäure in B hinein;
das Thermometer q dient zur Bestimmung der
Luft-Temperatur = t''.
Figur 6 stellt
einen Querschnitt der Rinne M, M in größerem Maaßstabe
dar. Dieselbe ist von Zinkblech angefertigt. Wie die Zeichnung zeigt, sind die Wände
doppelt, hohl und in verschiedene Canäle getheilt; diese Canäle sind in der Nähe des
Bodens der Rinne offen, und dienen dazu, die Luft in der Rinne sich frei bewegen zu
lassen, ohne daß eine wechselnde ungleiche Strömung stattfinden kann.
Die Nähe eines sehr heißen Ofens, welcher nach allen Seiten Wärmestrahlen aussendet,
macht jede genaue Beobachtung unmöglich; selbst schlecht leitende Schirme werden
bald heiß und wirken auf die Säule. Diesem Uebelstande habe ich dadurch abgeholfen,
daß ich ein mit Wasser gefülltes Gefäß, wie es Fig. 8 im Durchschnitte
und Fig. 9 in
vorderer Ansicht zeigt, an die Ofenwand stelle und die Rinne genau in die Oeffnung
a passe. Da aber auch das Wasser bald eine höhere
Temperatur annimmt, so ist dasselbe öfter zu erneuern. Zu diesem Ende wird die Dille
b durch einen Kautschukschlauch mit einem höher
gelegenen Gefäße verbunden, unddurch die Dille c dem bereits
erwärmten Wasser ebenfalls durch einen Kautschukschlauch Abfluß gegeben.
Die Rinne M, M muß genau sowohl an die Ofenwand C als an das Gefäß B
anstoßen, damit kein Luftstrom außer der Rinne an den beiden Flächen stattfinde.
Dieser Contact mit der Rinne, welcher in erster Linie nochwendig ist, hat jedoch den
Nachtheil, daß die Rinne selbst von diesen Endpunkten aus erwärmt wird, was auf die
Säule und auf den Multiplicator wirken kann. Wenn indessen die Temperatur der beiden
Flächen bald gleich ist, so kann dieser Einfluß nicht mehr störend seyn; übrigens
kann doch, bis dieser Zeitpunkt eintritt, die Säule selbst eine ungleiche Temperatur
bekommen, die sich dann nicht so leicht ausgleicht. Um eine Ausgleichung zu
bewirken, ziehe ich denjenigen der Schieber K welcher
auf der kälteren Seite der Säule ist, bis das Rheometer auf 0° zurückgeht und
nach Schließung des Schiebers bleibt.
Sonst ist das Verfahren ganz dasselbe wie dasjenige zur Bestimmung der
Leitungsfähigkeit des Materials der Ofenwand; die beobachtete Temperatur im Gefäße
B gibt den Werth =
t'.
Hätte man z.B. die Außenfläche der 0,755° dicken Ofenwand = e, von der Leitungsfähigkeit 0,4 = C und bei einer äußeren Temperatur = 15°,6 = t'', gleich 276°,5 =
t' gefunden, so wäre die Temperatur der inneren Wand:
Textabbildung Bd. 163, S. 334
Bei dieser Bestimmung der Temperatur des Ofens wird aber, genau genommen, nur
diejenige seiner inneren Wandfläche bestimmt, und diese wird nicht in allen Fällen
und an jeder Stelle des Ofens identisch seyn mit der Temperatur der
Verbrennungsproducte im Inneren des Ofens, sondern etwas kleiner und zuweilen auch
etwas größer als letztere. Die beobachtete Temperatur wird größer seyn: in dem Falle
wo die innere Temperatur nachgelassen hat, und die Wand noch von einer früheren
heftigeren Hitze afficirt bleibt; hingegen kleiner: 1) wenn überhaupt die Temperatur
des Ofens im Steigen begriffen ist, und 2) wenn die Verbrennungsproducte nicht in
vollständiger Berührung mit der Fläche sind, die zur Beobachtung dient.
In Fig. 7
dagegen trifft die Flamme, nachdem sie den Ofen passirt hat, nothwendig die Platte
C, und da der Raum über derselben enge ist, so
können die Ströme nicht in die Esse R. gelangen, ohne in
vollständigen Contact mit dem Meßapparat zu kommen. Nur wird diese Temperatur
diejenige seyn, welche das Feuer nach stattgehabter Wirkung im Ofennoch behält. Aber gerade diese
Temperatur zu kennen, ist oft am wichtigsten, und man kann von derselben leicht auf
die Temperatur im Ofen selbst schließen. – Wollte man den Meßapparat an der
Wand W anbringen, so würde anscheinend die Temperatur im
Ofen selbst angegeben, aber man würde sich dabei sehr täuschen können, da der mit
der Wand parallele Strom der Verbrennungsproducte nothwendig durch die Transmission
der Wand selbst eine etwas weniger heiße Schichte der Verbrennungsproducte
erzeugt.
Es wird also nöthig seyn, in jedem Falle die Stelle, an der man die Messung vornehmen
will, dem gesuchten Resultat entsprechend zu wählen.
Mein Streben gieng zunächst dahin, die Temperatur von Glas-Schmelzöfen zu
messen, und da solche ganze Monate und Jahre lang im Betrieb stehen, so werden
selbst 8 Zoll dicke Wände hinlänglich zuverlässige Resultate geben. Bei Oefen
hingegen, die nur zeitweise in Betrieb kommen, muß das Stück Ofenwand, welches zur
Temperaturbestimmung dienen soll, verhältnißmäßig von geringer Dicke genommen
werden, damit dasselbe schnell sich mit der ihm zukommenden Wärmemenge sättigt.
Die Genauigkeit und Zuverlässigkeit der Messungen hängt nun in erster Linie von der
Genauigkeit der Bestimmung der Leitungsfähigkeit – C ab, da eine Differenz von 0,01 in diesem Werthe, bei der Bestimmung von
t eine Differenz von 52° C. gibt. Es wäre
möglich, zur Bestimmung von C noch genauere Instrumente
anzuwenden, als die beschriebenen sind, wodurch dieselbe selbst genauer würde; wenn
man aber bedenkt, daß von den Materialien, welche der Prüfung unterworfen werden,
selbst wenn sie von ein und derselben Masse genommen werden, nie ein Stück dem
andern völlig gleich ist, so hat es keinen Werth genauere Bestimmungen vorzunehmen.
– Das einzig mögliche Mittel, in dieser Beziehung der Bestimmung von t eine größere Zuverlässigkeit zu geben, wäre, eine
feuerfeste Masse mit ganz besonderer Sorgfalt anzufertigen, die in ihrer
Leitungsfähigkeit durchaus nicht mehr variirt, und zu diesem Behufe würde dieselbe
beim Brennen einem Maximum von Temperatur auszusetzen seyn.
Eine andere Fehlerquelle bei diesen Bestimmungen ist die Entfernung der warmen
Flächen von der Säule; je kleiner dieselbe ist, desto genauer läßt sich die
Temperatur = t' bestimmen, größere Entfernungen geben
weniger genaue Resultate; indessen bei 8 Zoll Entfernung ist es immer noch möglich
für 3 Thermometergrade einen Rheometergrad zu beobachten, so daß durch zweckmäßige
Wahl der Dicke und Leitungsfähigkeitder Ofenwand, in dieser Beziehung sehr befriedigende
Resultate zu erhalten sind.
Werden daher alle diese Vorsichtsmaßregeln sorgfältig berücksichtigt und befolgt, so
kann immerhin angenommen werden, daß die in Thermometergraden ausdrückbare
Temperatur = t bis auf 50°, vielleicht bis auf
75° C. genau zu erhalten ist; eine solche Genauigkeit übertrifft gewiß weit
diejenige, welche alle bisher für die Praxis vorgeschlagenen Pyrometer gewähren.
Immerhin bietet die Bestimmung der Ofenwand-Temperatur t' nicht bloß das Mittel, daraus die innere Temperatur zu berechnen,
sondern auch sehr annähernd den Wärmeverlust, welchen ein Feuerungsapparat durch
Transmission der Wände erleidet.
Ebenso kann man mittelst meines ApparatesHr. Mechanicus Chr. Oechsle in Pforzheim erbietet
sich solche Apparate anzufertigen. die Temperatur der evacuirten Verbrennungsproducte bestimmen.
Bezeichnen wir daher mit W die Wärmemenge welche per Stunde in einem solchen Verbrennungsapparate
entwickelt wird, mit N den Nutzeffect, d.h. die Wärme
welche an den zu erwärmenden Körper übergeht, mit T die
Transmission und mit E die Evacuation, so haben wir zur
Controle:
W = N +
T + E
und da gerade das Verhältniß dieser Werthe für den Praktiker
das Gesuchte ist, so ist leicht einzusehen, daß mein Verfahren zur Bestimmung
desselben, dem Zwecke besser entspricht als alle bisher angewandten Methoden.
Offenburg, den 20. Februar 1862.
Tafeln