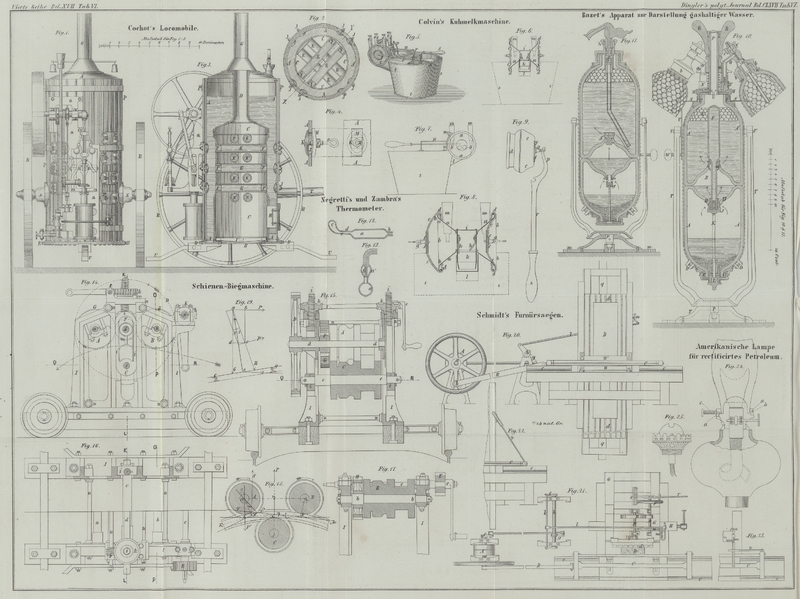
| Titel: | Beschreibung einer Schienen-Biegmaschine. |
| Fundstelle: | Band 167, Jahrgang 1863, Nr. CIII., S. 413 |
| Download: | XML |
CIII.
Beschreibung einer
Schienen-Biegmaschine.
Mit Abbildungen auf Tab.
VI.
Beschreibung einer Schienen-Biegmaschine.
Ehe ich auf die Beschreibung dieser Schienen-Biegmaschine näher eingehe, will
ich die Anwendbarkeit solcher Maschinen erörtern und zum besseren Verständniß vorerst
einige bisher üblich gewesene Biegungsarten in Kürze besprechen.
Bei dem Baue der älteren Bahnen Norddeutschlands wurde zur Herstellung der durchweg
schwachen Curven, folgendes praktische Verfahren angewandt, welches seiner
Einfachheit und Zweckmäßigkeit wegen sich bis jetzt erhalten hat. Man trieb neben
dem fertig gelegten Schienenstrange, an der convexen Seite vor den Köpfen der
Stoßschwellen, und an der concaven Seite vor den Köpfen der mittelsten
Zwischenschwellen, sogenannte Curvenpfähle in das Planum und regulirte demnächst die
Lage des Geleises durch Holzkeile, welche zwischen den Pfählen und den
entsprechenden Schwellenköpfen eingetrieben, die Schienenmitte gewaltsam in die
richtige Lage zwängen. Es wird diese Art der Schienenbiegung auch fernerhin mit
Vortheil bei schwachen Curven bis 500 Met. Radius oder 0,01 Met. Pfeilhöhe der 6
Met. langen Schiene Anwendung finden.
Bei Bahnbauten der jüngeren Zeit wandte man, durch locale Verhältnisse gezwungen,
Curven bis 200 Met. Radius oder 0,03 Met. Pfeilhöhe auf die 6 Met. lange Schiene an.
Eine gleich große Biegung haben die Schienen der Weichen-Curven. Liegen bei
Weichen der gerade und der gebogene Strang auf denselben Schwellen, so pflegt man,
nachdem das gerade Geleise fertig liegt, die Schienen der Curve an den Stößen
aufzuschrauben, zu verlaschen und demnächst ihre Mitte mit dem Wuchtbaume nach dem
Augenmaaße durchzusetzen und zu vernageln. Wenn hierbei die Nägel an der concaven
Seite so stark sind, daß sie nicht abgedrückt werden, so wird bei der Erschütterung
des fahrenden Zuges die gebogene Schiene sich um ihre halbe Pfeilhöhe strecken,
indem sie die Mittelschwellen nachschleppt und der entsprechenden Schiene des
Hauptgeleises eine gleich große Durchbiegung ertheilt. Dieses Verfahren ist demnach
zu verwerfen.
Werden aber zu dem Bettungsmaterial die beim Sprengen gewonnenen Steinschrote
benutzt, so ist das Eintreiben von Curvenpfählen nicht mehr möglich. Es müssen in
diesem Falle die Schienen vorher gebogen werden. Ohne Schienen-Biegmaschine
geschieht dieß auf folgende Art:
Man legt zwei Schwellen parallel zu einander, senkrecht zur Bahnachse, mit ihren
äußeren Kanten auf Schienenlänge auseinander, hält die zu biegende Schiene in eine
durch Versuch ermittelte Höhe darüber, und läßt sie gleichmäßig so fallen, daß die
beiden Enden auf die Schwellen aufschlagen. Die Mitte setzt sich dabei vermöge ihres
eigenen Gewichtes durch. Nach einiger Uebung erhalten die Arbeiter in dieser Art der
Biegung eine solche Sicherheit, daß sie jeder Schiene beim zweiten Wurf fast genau
die gewünschte Pfeilhöhe geben. Die Curve, nach welcher die Schiene gebogen ist, hat aber
mehr Aehnlichkeit mit einer Hyperbel als mit einem Kreisbogen und es erhalten
schlechte Schienen Knicke oder gar Brüche.
Aus diesem Grunde ist solches Biegen von den Bahnverwaltungen verpönt – und
sind zu dem Ende eigene Schienen – Bieg- und Streckmaschinen der
verschiedensten Art construirt worden. Eines der zweckmäßigsten Systeme ihrer
Construction ist in Fig. 18 gezeichnet. Drei Walzen A, B und C stehen im Dreieck zu einander. Die unterste C kann der gemeinsamen Achse a,
b der beiden anderen zwischen den Grenzen beliebig genähert oder davon
entfernt werden, wodurch ein größerer oder ein geringerer Biegungsgrad erzielt wird.
Eine oder zwei der Walzen werden durch irgend einen Mechanismus um ihre Achse
gedreht und so wird die Schiene durchgewalzt.
Wird auf einer dieser Maschinen eine Schiene nur wenig (0,0025 Met. auf die 6 Met.
lange Schiene) durchgebogen, so streckt sie sich, nachdem sie aus den Walzen tritt,
wieder gerade. Verstärkt man die Durchbiegung allmählich, so wird endlich ein Punkt
eintreten, bei welchem die äußersten, am meisten in Anspruch genommenen Fasern der
Schiene, über ihre Elasticitätsgrenze hinaus ausgereckt, resp. zusammengedrückt
werden. Es bildet sich für diese Fasern ein neuer, von dem ursprünglichen entfernt
liegender Gleichgewichtszustand. Auch jetzt streckt sich die Schiene zurück, aber
nicht ganz. Die besagten äußersten Fasern eines Schienenquerschnittes ziehen, resp.
dehnen sich bis zu ihrer neuen Gleichgewichtsgrenze. Alle übrigen der neutralen
Achse näher liegenden Fasern dagegen suchen ihre ursprüngliche Länge zu erreichen
und drücken resp. ziehen dabei die ersteren über ihre Gleichgewichtsgrenze hinaus.
Nachdem die Schiene ihre dauernde Durchbiegung erlangt hat, haben die äußeren Fasern
das Bestreben sie mehr zu krümmen, die inneren sie zu strecken, und diese beiden
Wirkungen halten sich das Gleichgewicht. Es erhellt hieraus, daß die Schiene einer
weiteren Biegung weniger Widerstand entgegensetzt. Wie viel die Rückbiegung beträgt,
hängt direct davon ab, wie viele der äußeren Fasern über ihre erste, resp. zweite
etc. Elasticitätsgrenze hinaus forcirt wurden, also:
1) von der Stellung der drei Walzen zu einander, und insofern
diese constant angenommen wird:
2) von der Beschaffenheit des Materials, und dieses als gleich
vorausgesetzt:
3) von dem Härtegrade, welchen das Eisen bei der schnelleren oder
langsameren Abkühlung erlangt hat, und endlich
4) von dem Material und Härteunterschiede der inneren und äußeren
Fasern ein und derselben Schiene.
Es können mithin zwei Schienen, zu denen die Luppen in einem Ofen gepuddelt und
welche aus demselben Schweißofen gewalzt wurden, bei gleicher Stellung der
Biegmaschine eine verschiedene Pfeilhöhe erlangen.
Der Biegungsunterschied verschiedener Schienen beträgt bei derselben Stellung der
Maschine für verschiedene Schienen desselben Querschnitts bis 0,02 Met. Es ist daher
nicht möglich, durch Versuche eine Scala an der Stellvorrichtung einer
Schienen-Biegmaschine zu ermitteln, mit deren Hülfe man Schienen nach Wunsch
biegen könnte; die richtige Biegung muß bei jeder einzelnen Schiene durch den
Versuch erreicht werden und dabei ergeben sich folgende Resultate:
Soll eine Schiene um 0,02 Met. Pfeilhöhe gebogen werden, und erzielt man beim ersten
Durchwalzen nur 0,01 Met., so wird man die untere Walze um das doppelte η2 Fig. 18 durchstellen. Bei
einem abermaligen Durchwalzen erhält man nun vielleicht 0,25 Met. an Stelle der
erwarteten 0,2 Met. Pfeilhöhe. Versucht man eine kleine entsprechende Rückbiegung,
so wird die Schiene unverhofft wieder nahezu gerade.
Solche Resultate sind sehr überraschend und entmuthigend für den beaufsichtigenden
Beamten. Der Grund ist in der oben erwähnten gestörten Harmonie der Wirkungsweise
einzelner Fasern eines Schienenquerschnittes zu suchen. Die
Schienen-Biegmaschine verliert hierdurch viel an ihrem praktischen Werth,
welcher ihr jedoch durch eine geeignete Anordnung wieder gegeben werden kann.
Sehr falsch ist es, eine Biegmaschine nach jeder einzelnen Curve hin dirigiren zu
wollen, um dort während des Oberbaues die Biegung vorzunehmen. Da das Biegen der
Schienen auf eine bestimmte Pfeilhöhe unmöglich mit dem Legen Schritt halten kann
und in solchen Fällen Zeitverlust Geld ist, so verspüren die Herren Unternehmer
wenig Lust sich mit der ihnen ganz unbekannten Maschine erst vertraut zu machen. Sie
ziehen die älteren Biegungsarten durch Curvenpfähle oder Werfen der Schienen vor und
die Beamten sehen sich gezwungen, dem allgemeinen Drängen Rechnung tragend, ein Auge
zuzudrücken. Die Maschine wird dann vorschriftsmäßig auf der Strecke herumgeschleppt
und sollte sie auch wirklich an einem Punkte rechtzeitig eintreffen, doch selten
gebraucht.
Anders gestalten sich die Verhältnisse, wenn die Biegmaschine in dem Walzwerke oder
an einer Station aufgestellt wird, über welche der Schienentransport geht. Aus der
Anzahl der Schienen für jeden einzelnen Curvenradius auf der ganzen Strecke und
deren Gesammtzahl ermittelt man den Procentsatz für jeden einzelnen Biegungsgrad,
welche Procentsätze man
beim Biegen möglichst einzuhalten sucht. Man stelle nun nicht die Maschine für jede
einzelne Schiene, sondern sortire die Schienen, welche bei einer bestimmten Stellung
derselben durchgewalzt sind, nach den verschiedenen Biegungsgraden, wobei die
variirenden Pfeilhöhen zu dem nächst höheren Biegungsgrad gerechnet werden.
Hauptregel muß dabei bleiben, zuerst die am stärksten gebogenen Schienen fertig zu
walzen. Die sogenannten Differenz-Schienen, welche die Längenunterschiede des
inneren und äußeren Stranges in einem Curvengeleise vermitteln sollen, werden in
derselben Weise zuerst gebogen. Jeder Sendung von Curvenschienen wird die nöthige
Anzahl Differenz-Schienen beigegeben. Es wird dadurch gleichzeitig das
irrthümliche Einlegen der letzteren in die gerade Strecke verhindert. Rathsam ist
es, jede Schiene mit ihrem Curvenradius am Kopfe zu stempeln. Verwendet man zu
diesen Arbeiten dieselben Leute, so kann das Biegen bei geeigneter Anzahl von
Maschinen dem Legen des Oberbaues Schritt halten. Es ist vortheilhaft, sämmtliche
Schienen um 0,0025 Met. bis 0,0075 Met. weniger zu biegen, als dem Curvendurchmesser
entspricht, wie ich nun beweisen werde.
Fällt man von dem höchstgelegenen Schwerpunkte a
Fig. 19 eines
Waggons ein Perpendickel ae gegen die Ebene der
beiden Schienenoberkanten fg, so muß, wenn ein
Schnellzug mit derselben Sicherheit in Bezug auf Umschlagen durch die Curve brausen
soll, mit der ein Waggon ruhig darin steht, die Resultirende R aus der Centrifugalkraft P bei der größten
Fahrgeschwindigkeit v und der Schwerkraft G ebenso weit nach außen von dem Perpendikel ae abweichen, als die Richtung ad der Schwerkraft sich nach innen davon
entfernt.
Für einen Curvenhalbmesser r ist die Centrifugalkraft
P = v²G/gr
und die tang α des Winkels
welchen die Richtung der Resultirenden R mit der
Lothrechten bildet
tang α = ab/bc = P/G = v²G/grG =
v²/gr
der Neigungswinkel
β = α/2, also für kleine Winkel tang
β = tang α/2 = v²/2gr.
Die Ebene der Schienenoberkanten bildet ein Stück des
Kegelmantels, dessen Spitze um r . tang β unter der Horizontalebene liegt;
h = r .
v²/2gr = v²/2g,
also ist h eine constante Größe.
Die Geschwindigkeit w, bei welcher ein Zug auf der so
geneigten Bahn die beiden Schienen gleichmäßig angreift, mithin die Resultirende R in die Richtung ae
fällt:
tang β = w ²/gr = v²/2rg
w ² = v ²/2 oder w = v/√2, nahezu 2/3 v.
Wenn v der Schnellzuggeschwindigkeit entspricht, so wird
2/3 v nahezu die Güterzuggeschwindigkeit seyn.
Bei einer Ueberhöhung, entsprechend dem Winkel β,
drückt sich der Radflantsch mit einer Kraft p an die
äußere Schiene;
p = R sin
β
und R = P/sin α, also p = P sin β/sin
α; für kleine Winkel
p = 1/2 P.
Auf den Strecken wo die Züge meist mit voller Geschwindigkeit durch schwache Curven
fahren müssen, hat man die Ueberhöhung noch größer genommen. Wird
β = α, also tang β = v²/gr oder h = v²/g,
so drückt der Schnellzug mit keiner Seitenkraft gegen die
äußere Schiene, wird also im erweiterten Curvenstrange hin und her schlagen, ähnlich
wie in einem geraden Strange bei zu weiter Spur. So groß soll deßhalb die
Ueberhöhung, wenn auch sonst zulässig, nie genommen werden. Die Grenze für die
Ueberhöhung tritt dort ein, wo G zu nahe an die innere
Schiene f fällt, also der Wagen im labilen Gleichgewicht
steht. Es ist in solchem Falle vorgekommen, daß schiefgeladene Wagen beim Halten
eines Zuges in der Curve umgefallen sind. Wo die Grenze eintritt, dieß hängt
lediglich von der Bauart der Waggons ab. Es ist sehr zu tadeln, daß neuere Bahnen,
welche ihre Züge mit großer Geschwindigkeit durch starke Curven fahren lassen
müssen, ihre Personenwagen unverantwortlich hoch bauen, nur um denselben ein stolzes
Ansehen zu geben.
Da die Kraft so nie ganz verschwinden soll und für gewöhnliche Ueberhöhung p = 1/2 P der halben
Centrifugalkraft für schnellfahrende Züge ist, so wird der Radflantsch noch mit
einer großen Kraft gegen die äußere Schiene gepreßt. Die Stoßschwellen liegen meist
fester als die Mittelschwellen. Die Mitte der vollkommen gebogenen Schiene, welche
einen Theil ihrer Widerstandsfähigkeit verloren hat, setzt sich mit den
Mittelschwellen nach Außen durch und da der am inneren Kopfe dieser Schwellen
entstehende Raum sich beim Rütteln des Zuges füllt, so bleibt sie dauernd überbogen.
Legt man bei starken Curven die Mittelschwellen durch Curvenpfähle fest, so drücken
sich die Nägel an der convexen Seite des äußeren Stranges ab und die Schiene
überbiegt sich dennoch. Am meisten macht sich dieß in den waagrechten Weichencurven
bemerkbar, wo selbst doppelte Nagelung unzureichend ist. Es ist deßhalb
vortheilhaft, die Schienen so viel weniger zu biegen, als man ohne Curvenpfähle
durch den Widerstand des Bettungsmaterials gewaltsam durchzusetzen im Stande ist. Es
wirkt dann die Schiene vermöge ihrer Elasticität dem Drucke des Radflantsches
entgegen und die Stöße gegen die äußeren Nägel sind dadurch gebrochen. Auch selbst
wenn die Schiene dauernd wenig unterbogen bleibt, so ist dieß nicht so gefährlich,
als überbogene Schienen es sind, bei denen die Stöße scharf vortreten.
Beschreibung der Maschine. – Die
Schienen-Biegmaschine, von welcher Fig. 14 die Ansicht, Fig. 15 einen
Querschnitt nach LK, Fig. 16 oben zur Hälfte
einen Horizontalschnitt nach QR und unten eine
obere Ansicht mit fehlenden Walzen etc., endlich Fig. 17 einen Querschnitt
nach OP darstellt, wurde beim Bau der
links-rheinischen Bahn benutzt.
In zwei festen, durch Distanzstangen verbundenen Böcken J,
J liegen zwei Walzen A und B mit den Achsen a und b in festen Lagern. Eine dritte Walze C hängt mit ihrer Achse c in
zwei Bügeln i, welche sich in den Ständern J führen und oben in zwei Schrauben i, i enden. Diese Schrauben gehen in zwei Messingmuttern
k, k, welche auf den Ständerdeckeln drehbar sitzen.
An den Muttern k sind Schneckenräder angegossen, welche
durch die gemeinsame Schneckenwelle e, e mit daran
sitzender Kurbel gleichzeitig bewegt werden, wodurch die Schraube und mit ihr die
untere Walze C gleichmäßig gehoben und gesenkt werden
kann. Auf dem Schneckenrade kann eine Eintheilung entsprechend η2 Fig. 18, durch Versuch
ermittelt, angebracht werden. Auf den Wellen a und b der festen Walzen A und
B sitzen die beiden Zahnräder G und H, in welche das gemeinsame Getriebe F eingreift. Letzteres sitzt auf der Welle d, d, welche in Fig. 15 in den Böcken
gelagert links durchgeht und auf ihrem Kopfende das Zahnrad D trägt, welches in das Getriebe E der
Kurbelwelle e eingreift. Fig. 15 zeigt in die
Walzen links das Kaliber der Schiene eingegossen, rechts ein quadratisches Kaliber,
um die in der
Höhenrichtung krumm gefahrenen Schienen wieder zu strecken. Die Maschine ist auf
einen kleinen Bahnwagen aufgeschraubt.
Die Kraftverhältnisse der Schienen-Biegmaschine
lassen sich berechnen wie folgt:
Tritt die Schiene Fig. 18 in der Richtung μδ in
die Walzen, so stößt sie bei δ auf den Umfang der
Walze A und es wird ihr auf dem Wege δε eine Durchbiegung ηλ = m
ertheilt. Um der Schiene auf die Länge εδ
oder nahezu ab = l
eine Durchbiegung in zu ertheilen, muß in der Richtung cηεη eine Kraft darauf wirken
P = 48 (m
. EB)/l³.
Im vorliegenden Falle ist B das Trägheitsmoment eines
links-rheinischen Schienenquerschnittes nahezu = 4; der
Elasticitäts-Modulus. E = 25000000 Pfd.
Zollgewicht, l = 18'' preuß.
P = (48 . 25000000 . 4)/5832 m = 823045 . m
Die Schiene spannt sich gegen die Walze A im Punkte ε mit einer Kraft P¹ = 1/2 P.
Die Spannungen der Schiene verhalten sich (zwischen Grenzen) wie die Durchbiegungen.
Also herrscht in einem Punkte x des Weges δε, dessen Radius ax mit αε den Winkel α bildet
und welcher in einer Entfernung n unter φδ liegt, eine Spannung
S = P¹n/φε = n/2m P¹= P/4m n
und da, wie aus Fig. 18 ersichtlich,
n = r
(cos α – cos
β) ist
I. S = Pr/4m (cos α –
cos β).
Die Kraft K, welche im Punkte x angreifend, am Umfange der Walze der Spannung S das Gleichgewicht hält
II. K = S sin
α
= Pr/4m sin
α (cos α – cos
β)
K = Pr/4m (sin α cos
α – cos β sin
α)
dK/dα =
Pr/4m (– sin
α² + cos α – cos
β cos α) = 0
2 cos² α – cos β cos α – 1 = 0
cos α² – cos β/2 cos α
= 1/2
(cos α – cos
β/4)² = 1/2 + cos² β/16
III. Textabbildung Bd. 167, S. 420
Aus der Figur ergibt sich die Formel:
IV. cos
β = (r – 2 m)/r = 1 – 2m/r.
Nehmen wir m = 1''' preuß. als Maximaldurchstellung,
welche einem Radius von 40,5' entspricht, so ist
m = 0,0833
IV. cos
β = 1 – 0,1666/5 = 1 – 0,0833 = 0,9667 (β = 15º)
III. Textabbildung Bd. 167, S. 420
sin α = 0,1487
I. S = Pr/4m (0,9889 –
0,9667) = (823045 . 5)/4 0,0222
S = 22840 Pfd. Zollgewicht.
II. K = 22840
. sin α = 22840 . 0,1487 = 3396 Pfd.
Zollgewicht.
Mit kleiner Vernachlässigung wirkt S an jeder der beiden
oberen Walzen einfach und an der unteren doppelt, also bei der Stellung entsprechend
Winkel α wirken 4 S =
91360 Pfd. Zollgewicht auf Zapfenreibung.
Die beiden oberen Walzen haben Zapfen von 2'', die untere hat solche von 2 1/2'', wir
können also mit Berücksichtigung der sonstigen ZapfenreibungReibung 2,25 durchschnittlich annehmen. Die Zapfenreibung
k =
8 S . 1,125μ/(5–1,125μ) =
182720 . 0,023 (μ = 0,1)
k =
4202,5 Pfd. Zollgewicht
K +
k =
7600 Pfd. Zollgewicht.
Bei der Uebersetzung 1: 30 des Bewegungsmechanismus müssen also an der Kurbel
wirken
7600/30 = 253 Pfd. Zollgewicht.
Es müssen demnach vier Mann anfassen, und jeder hat noch mit 65 Pfd. Zollgewicht zu
arbeiten; dieser Kraftaufwand dauert jedoch nur einen Moment und wird durch die,
wenn auch kleine Schwungkraft der Maschine schon etwas überwunden.
Wenn der Schienenkopf bis zum Punkte ε vorgerückt
ist, so wird S = 1/2 P und
sin α = 0, also
K = S .
sin α = 0.
Es ist dieß jedoch eine Täuschung. Bei der Aufstellung der Formel wurde nämlich
angenommen, der Bogen εηϑ sey ein
an die drei Walzen tangirender, und dieß hat auf die Berechnung bis jetzt wenig
Einfluß. Es verhalten sich aber die verschiedenen n',
n'' wie die entsprechenden l'³ l''³, also ist die Gleichung
der Curve y ³ – ax die der kubischen Parabel.
Ein Punkt ξ der Schienencurve liegt unterhalb des
Bogens, nach welchem sich die Schiene bewegt, muß also von der Walze C aus seiner natürlichen Lage gehoben werden. Die dazu
erforderliche Kraft Q, in der Richtung ϑεεϑ an der Schiene wirkend gedacht, berechnet sich wie folgt:
Ql = (ΣS + S' + S''' + S'''' + S
n)/n . m
und da die Spannungen den Durchbiegungen proportional sind
Ql = P/2
m
Q = Pm/2l = 823045 m²/36;
für m = 4/12
Q = 158,7 Pfd. Zollgewicht.
Es wirken jetzt auf Zapfenreibung 2P und erzeugen eine
Reibung
q = 4P .
1,125μ/(5 – 1,125μ) = 3292180 . 0,023 m = 6312 Pfd. Zollgew.;
also Q + q = 6470 Pfd. Zollgewicht;
an der Kurbel mithin 6470/30 = 216 Pfd.
Folglich arbeitet jeder der vier Mann noch mit 54 Pfd. Zollgewicht. Solche starke
Biegungen kommen aber auch nur für Drehscheibenkränze vor und in diesem Falle wird
man mehrmaliges Walzen vorziehen.
Für eine Curve von 50º Radius beträgt die Durchbiegung 0,0055'' auf 18''
Länge; nehmen wir die Durchstellung mit Rücksicht auf die Rückbiegung m = 0,02'' an, so wird:
IV. cos β = 0,992 (β = 7º)
III. Max. cos α = 0,99735 (α = 4º 10' 20'')
sin
α = 0,07275
I. S = 5504
II. K = 400
Pfd. Zollgewicht
k =
1013 Pfd. Zollgewicht.
Es müssen an der Kurbel wirken 1413/30 = 47 Pfd. Zollgewicht; also zwei Mann mit je
23 Pfd. bei dem größten Werthe von K.
Die Stellvorrichtung hat eine Uebersetzung von 3500 : 1. Bei 50 Pfd. Druck an der
Handkurbel ist die Durchstellung
m . 823045 = 50 . 3500
m = 175000/823045 = 0,21'' preuß. auf
18'' Länge
mit Vernachlässigung der Reibung, und P ist in diesem Falle
P = 823045 . 0,21 = 172839 Pfd.
Zollgewicht.
C. S.
Tafeln