| Titel: | Ueber die Construction von Saccharometern nebst dazu gehörenden Procent-Thermometern, mit deren Anwendung man bei jedem Temperaturgrade zwischen dem Frost- und Siedepunkte den Concentrationsgrad einer Zuckerlösung sofort ersehen kann; von Dr. G. Th. Gerlach. |
| Autor: | G. Th. Gerlach |
| Fundstelle: | Band 172, Jahrgang 1864, Nr. XIV., S. 31 |
| Download: | XML |
XIV.
Ueber die Construction von Saccharometern nebst
dazu gehörenden Procent-Thermometern, mit deren Anwendung man bei jedem
Temperaturgrade zwischen dem Frost- und Siedepunkte den Concentrationsgrad einer
Zuckerlösung sofort ersehen kann; von Dr. G. Th. Gerlach.
Mit einer graphischen Darstellung auf Tab. II.
Gerlach, über die Construction von Saccharometern nebst dazu
gehörenden Procent-Thermometern für Zuckerfabriken.
Um die specifischen Gewichte der Zuckerlösungen bei den Temperaturen zwischen dem
Frostpunkte und dem Siedepunkte berechnen zu können, ist es nöthig:
erstens die specifischen Gewichte der Zuckerlösungen von
den verschiedenen Concentrationsgraden bei irgend einer Normaltemperatur genau zu
wissen;
zweitens die Ausdehnungen der Zuckerlösungen von den
verschiedenen Concentrationsgraden zu kennen, welche diese Lösungen durch die
Temperaturveränderungen zwischen dem Frostpunkte und dem Siedepunkte erleiden.
Beide Aufgaben sind von dem Verfasser gelöst worden und mögen hier Platz finden.
Tabelle der specifischen Gewichte der
Zuckerlösungen bei 17°,5 C. für die
einzelnen Procentgehalte von 1 Procent bis 75 Procent.
Procent-gehalt.
SpecifischesGewicht.
Procent-gehalt.
SpecifischesGewicht.
Procent-gehalt.
SpecifischesGewicht.
Procent-gehalt.
SpecifischesGewicht.
75
1,383342
56
1,266600
37
1,164056
18
1,074356
74
1,376822
55
1,260861
36
1,159026
17
1,069965
73
1,370345
54
1,255161
35
1,154032
16
1,065606
72
1,363910
53
1,249500
34
1,149073
15
1,061278
71
1,357518
52
1,243877
33
1,144150
14
1,056982
70
1,351168
51
1,238293
32
1,139261
13
1,052716
69
1,344860
50
1,232748
31
1,134406
12
1,048482
68
1,338594
49
1,227241
30
1,129586
11
1,044278
67
1,332370
48
1,221771
29
1,124800
10
1,040104
66
1,326188
47
1,216339
28
1,120048
9
1,035961
65
1,320046
46
1,210945
27
1,115330
8
1,031848
64
1,313946
45
1,205589
26
1,110646
7
1,027764
63
1,307887
44
1,200269
25
1,105995
6
1,023710
62
1,301868
43
1,194986
24
1,101377
5
1,019686
61
1,295890
42
1,189740
23
1,096792
4
1,015691
60
1,289952
41
1,184531
22
1,092240
3
1,011725
59
1,284054
40
1,179358
21
1,087721
2
1,007788
58
1,278197
39
1,174222
20
1,083234
1
1,003880
57
1,272379
38
1,169121
19
1,078779
0
1,000000
Die unten folgende Tabelle A enthält die scheinbaren Ausdehnungen der Zuckerlösungen bei den
verschiedenen Temperaturen zwischen dem Frostpunkte und dem Siedepunkte, das Volumen
der Zuckerlösungen bei 17°,5 C. als Einheit angenommen. Die in derselben
mitgetheilten Volumenveränderungen der Zuckerlösungen wurden auf zweierlei Weise
bestimmt und zwar erstens mit einem Gewichtsaräometer, zweitens mit einem
Dilatometer.
Beide Versuchsreihen stimmten in sehr befriedigender Weise überein, indem sich nur
hier und da geringe Abweichungen herausstellten, die aber selten größer als ein oder
zwei Einheiten in der vierten Decimalstelle betrugen.
Beide Versuchsreihen waren also mit gläsernen Instrumenten angestellt, und geben
deßhalb die scheinbare Ausdehnung der Zuckerlösungen an,
denn da jedes gläserne Gefäß bei den Temperaturveränderungen sein Volumen ändert, so
kann die wirkliche Ausdehnung erst aus der gefundenen
scheinbaren Ausdehnung durch Multiplication mit dem Glasvolumen berechnet
werden.
Beispiel: Ein hohler Glaskörper, welcher bei 0°
Cels. 1,000000 Einheiten faßt oder verdrängt, wird bei 17°,5 C. 1,0004525
Einheiten fassen oder verdrängen, aber bei 50° C. 1,0012930 derselben
Einheiten.
Eine Flüssigkeit, welche bei
17°,5 C. 1,000000
Volumina einnahm, deren scheinbare Ausdehnungaber bei der Anwendung
von Glasgefäßen bei
50° C. zu 1,012197
Volumina gefunden wurde (wie dieß z.B. bei einer 40procentigen
Zuckerlösung der Fall war) wird in Wahrheit bei 50° C. das Volumen einnehmen
1,012197 × 1,0012930/1,0004525 = 1,013047 Volumina, vorausgesetzt, daß ihr
Volumen bei 17°,5 C. als Einheit angenommen bleibe.
Die specifischen Gewichte verhalten sich umgekehrt wie die Volumina; man kann daher
leicht aus einem bekannten Volumen bei einer bestimmten Temperatur und einem
bekannten specifischen Gewichte, für jene erwähnte Temperatur das specifische
Gewicht berechnen.
Beispiel: Das specifische Gewicht einer 40procentigen
Zuckerlösung, bezüglich auf die Temperatur von 17°,5 Cels. ist 1,179358.
Wurde das Volumen dieser 40procentigen Lösung bei 17°,5 Cels. = 1,000000
angenommen, so wurde das scheinbare Volumen bei
50° C. = 1,012197 gefunden; das scheinbare
specifische Gewicht dieser Lösung bei 50° C. ist also
1,179358/1,012197 = 1,165147.
Diesem specifischen Gewichte bei 50° C. liegt als Einheit Wasser von
17°,5 C. zu Grunde.
Das scheinbare specifische Gewicht ist also ein solches, wie
es ein gläsernes Instrument direct beim Einsenken in eine heiße Zuckerlösung
anzeigt; dem scheinbaren specifischen Gewichte liegen nicht die Gewichtsmengen
absolut gleichgroßer Volumina als Vergleich zu Grunde, sondern derjenigen
Volumina, wie sie durch die Glasausdehnung bedingt werden.
Wollte man aus dem scheinbaren specifischen Gewichte, das
wirkliche specifische Gewicht ableiten, d.h.
dasjenige specifische Gewicht, welchem als Vergleich die Gewichtsmengen absolut
gleichgroßer Volumina der zu untersuchenden Flüssigkeit einerseits und reinen
Wassers von einer bestimmten Temperatur andererseits zu Grunde liegen, so würde es
nöthig seyn das scheinbare specifische Gewicht durch die Glasausdehnung zu
dividiren.
Beispiel: das wirkliche specifische Gewicht der
40procentigen Zuckerlösung berechnet sich für die Temperatur von 50° C. wie
folgt:
(1,179358 × 1,0004525)/(1,012197 × 1,0012930) =
1,164169.
Diesem wirklichen specifischen Gewichte liegen als Vergleich die Gewichtsmengen
gleichgroßer Volumina einer 40procentigen Zuckerlösung von 50° C. einerseits,
und reinen Wassers von 17°,5 C. andererseits zu Grunde.
„Für die Praxis hat es hohen Werth, das spec. Gewicht der Zuckerlösungen
bei den verschiedenen Temperaturen zu kennen, jedoch wird selten der Fall
eintreten, daß die Kenntniß der specifischen Gewichte von Werth sey, Wasser von
gleicher Temperatur als Einheit gesetzt.
Will man z.B. das spec. Gewicht einer Zuckerlösung bei 50° C. wissen, so
wird man diesem spec. Gewichte nicht Wasser von 50° C. als Einheit zu
Grunde legen wollen, sondern in den meisten Fällen Wasser von 17°,5 C.,
da die Instrumente, mit welchen die spec. Gewichte ermittelt werden (meistens
Scalen-Aräometer) in den bei Weitem am häufigsten Fällen auf die
Temperatur von 17°,5 C. geaicht wurden.
Die Ausdehnung, welche die gläsernen Instrumente beim Einsenken in die heißen
Flüssigkeiten durch den Einfluß der Wärme erleiden, ist aber die Ursache,
weßhalb man mit diesen Instrumenten auch immer nur die scheinbaren und nicht die
wirklichen specifischen Gewichte erhält, und für die
Praxis haben daher auch nur die scheinbaren specifischen Gewichte
Werth.
Eine solche Tabelle für die scheinbaren specifischen Gewichte bei den
verschiedenen Temperaturen ist also berechnet worden und zwar nach der Formel
S/V,
in welcher Formel S das specifische Gewicht der
Zuckerlösung bei 17°,5 C. ist, Wasser von 17°,5 C. = 1,
V aber das scheinbare Volumen dieser Zuckerlösung
bei den verschiedenen Temperaturen, das Volumen der Lösung bei 17°,5 C. =
1.
Allen diesen specifischen Gewichten liegt also Wasser von 17°,5 C. als
Einheit zu Grunde, es sind scheinbare specifische Gewichte, d.h. solche, wie sie
ein gläsernes Instrument direct beim Versuch anzeigt, z.B. ein gläsernes
Scalen-Aräometer, welches für die Temperatur von 17°, 5 C. geaicht
wurde.
Siehe die unten folgende Tabelle B.
Da die Gesetze der Ausdehnungen von Zuckerlösungen durch Curven repräsentirt
werden, so müssen auch die specifischen Gewichte ein und
derselben Zuckerlösung bei verschiedenen Temperaturen in ihrer
graphischen Verbindung Curven bilden. Die einzelnen Punkte dieser Curven bei 5
zu 5 Grad Temperaturzunahme lassen sich aus der Tabelle B entnehmen; die Zwischenglieder aber lassen sich durch Interpolation
finden.
Man begeht keinen sehr großen Fehler, wenn man die Verbindung der bekannten
Punkte sich durch gerade Linien vorgenommen denkt und alle Zwischenglieder
lassen sich alsdann berechnen nach der Formel:
(d . D')/D + s = x.
In eben erwähnter Formel ist:
d die Differenz zwischen dem größeren spec. Gewichte
der betreffenden Lösung bei der niederen Temperatur und dem kleineren
specifischen Gewichte bei der höheren Temperatur;
D ist die Differenz zwischen der höheren Temperatur
und der niederen Temperatur, auf welche sich die beiden gegebenen specifischen
Gewichte beziehen;
D' ist die Differenz, welche sich ergibt beim Abzug
der niederen von den beiden gegebenen Temperaturen, auf welche sich die beiden
gegebenen specifischen Gewichte beziehen von der bekannten, zwischen den beiden
gegebenen liegenden Temperatur, für welche das unbekannte specifische Gewicht
gesucht werden soll;
s ist das kleinere der beiden gegebenen specifischen
Gewichte, bezüglich auf die höhere Temperatur, und
x ist das zu suchende specifische Gewicht als
Zwischenglied zwischen den beiden bekannten specifischen Gewichten.
Will man hingegen durch Interpolation die Temperatur kennen lernen, bei welcher
eine gegebene Lösung ein bestimmtes spec. Gewicht zeigt, so bedient man sich der
Formel:
(D . d')/d + t = x
in welcher Formel
d die Differenz ist zwischen dem größeren spec.
Gewichte der betreffenden Lösung bei der niederen Temperatur und dem kleineren
spec. Gewicht derselben Lösung bei der höheren Temperatur;
d' ist die Differenz zwischen dem größeren spec.
Gewichte bei der niederen Temperatur und dem gegebenen spec. Gewicht, für welche
die Temperatur gesucht werden soll;
D ist die Differenz zwischen der höheren Temperatur
und der niederen Temperatur, auf welche die beiden gegebenen spec. Gewichte sich
beziehen;
t ist die niedere der beiden gegebenen Temperaturen
und
x ist die zu suchende Temperatur, bei welcher die
Lösung von bekanntem Procentgehalte das gegebene spec. Gewicht zeigt.
Nach dieser zuletzt entwickelten Formel findet man, daß
die 5procentige
Zuckerlösung
bei
6°,6 C. das
spec.
Gew. der
5,2 procent.
Lösung
zeigt =
1,020893
„
12,3
„
„
5,1 „
„
1,020491
„
17,5
„
„
5
„
„
1,019686
„
25,8
„
„
4,5 „
„
1,017689
„
32,8
„
„
4
„
„
1,015691
„
43,8
„
„
3
„
„
1,011725
„
53,0
„
„
2
„
„
1,007788
„
61
„
„
1
„
„
1,003880
„
68,45
„
„
0
„
„
1,000000
Die 10procentige
Zuckerlösung
zeigt bei
0°,9 C. das
spec.
Gew. der
10,4
procent.
Lösung
=
1,041792
9,2
„
„
10,3
„
„
1,041356
12,4
„
„
10,2
„
„
1,040948
15,3
„
„
10,1
„
„
1,040521
17,5
„
„
10
„
„
1,040104
25,5
„
„
9,5
„
„
1,038037
zeigt bei
32°,4 C. das
spec.
Gew. der
9
procent.
Lösung
=
1,035961
43,3
„
„
8
„
„
1,031848
52,6
„
„
7
„
„
1,027764
60,9
„
„
6
„
„
1,023710
68,7
„
„
5
„
„
1,019686
75,9
„
„
4
„
„
1,015691
82,4
„
„
3
„
„
1,011725
88,5
„
„
2
„
„
1,007788
94,3
„
„
1
„
„
1,003880
99,9
„
„
0
„
„
1,000000
Die 20procentige
Zuckerlösung
zeigt bei
5°,9 C. das
spec.
Gew. der
20,5
procent.
Lösung
=
1,085477
17,5
„
„
20
„
„
1,083234
31,6
„
„
19
„
„
1,078779
42,6
„
„
18
„
„
1,074356
52,0
„
„
17
„
„
1,069965
60,8
„
„
16
„
„
1,065606
68,9
„
„
15
„
„
1,061278
76,3
„
„
14
„
„
1,056982
83,1
„
„
13
„
„
1,052716
89,4
„
„
12
„
„
1,048482
95,6
„
„
11
„
„
1,044278
Die 30procentige Lösung
zeigt bei
9°,2 C. das
spec.
Gew. der
30,5
procent.
Lösung
=
1,131996
17,5
„
„
30
„
„
1,129586
31,2
„
„
29
„
„
1,124800
42,4
„
„
28
„
„
1,120048
52,0
„
„
27
„
„
1,115330
61
„
„
26
„
„
1,110646
69,3
„
„
25
„
„
1,105995
77,2
„
„
24
„
„
1,101377
84,5
„
„
23
„
„
1,096792
91,3
„
„
22
„
„
1,092240
97,9
„
„
21
„
„
1,087721
Die 40procentige
Zuckerlösung
zeigt bei
–
0°,18 C. das
spec.
Gew. der
41
procent.
Lösung
=
1,184531
+
9,8
„
„
40,5
„
„
1,181945
zeigt bei
17°,5 C. das
spec.
Gew. der
40
procent.
Lösung
=
1,179358
30,9
„
„
39
„
„
1,174222
42,0
„
„
38
„
„
1,169121
52,0
„
„
37
„
„
1,164056
61,0
„
„
36
„
„
1,159026
69,6
„
„
35
„
„
1,154032
78,0
„
„
34
„
„
1,149073
85,9
„
„
33
„
„
1,144150
93,3
„
„
32
„
„
1,139261
Die 50procentige
Zuckerlösung
zeigt bei
1°,96 C. das spec. Gew. der
51 procent. Lösung
=
1,238293
17,5
„ „
50
„ „
1,232748
30,4
„ „
49
„ „
1,227241
41,9
„ „
48
„ „
1,221771
52,2
„ „
47
„ „
1,216339
61,8
„ „
46
„ „
1,210945
70,9
„ „
45
„ „
1,205589
79,5
„ „
44
„ „
1,200269
87,6
„ „
43
„ „
1,194986
95,3
„ „
42
„ „
1,189740
Die 60procentige
Zuckerlösung
zeigt bei
3°,1 C. das
spec.
Gew. der
61
procent.
Lösung
=
1,295890
17,5
„
„
60
„
„
1,289952
30,7
„
„
59
„
„
1,284054
42,4
„
„
58
„
„
1,278197
52,9
„
„
57
„
„
1,272379
62,9
„
„
56
„
„
1,266600
72,5
„
„
55
„
„
1,260861
81,5
„
„
54
„
„
1,255161
90,1
„
„
53
„
„
1,249500
98,4
„
„
52
„
„
1,243877
Die 70procentige
Zuckerlösung
zeigt bei
3°,3 C. das
spec.
Gew. der
71
procent.
Lösung
=
1,357518
17,5
„
„
70
„
„
1,351168
31,0
„
„
69
„
„
1,344860
43,8
„
„
68
„
„
1,338594
55,1
„
„
67
„
„
1,332370
zeigt bei
65°,5 C. das
spec.
Gew. der
66
procent.
Lösung
=
1,326188
75,0
„
„
65
„
„
1,320046
84,4
„
„
64
„
„
1,313946
93,4
„
„
63
„
„
1,307887
Scalen-Aräometer, welche statt der specifischen Gewichte direct den
Procentgehalt der Zuckerlösungen angeben, nennt man Saccharometer. Ein für die
Temperatur von 17°,5 geaichtes Saccharometer wird also bei den eben
genannten Temperaturen zwischen 0 und 100° C. die angegebenen
Procentgehalte der Zuckerlösungen anzeigen und weil die Zuckerlösungen durch
Wärme specifisch leichter, durch Kälte specifisch schwerer werden, wird der
angezeigte Procentgehalt bei Temperaturen über 17°,5 geringer, bei
Temperaturen unter 17°,5 aber größer seyn, als der wahre Procentgehalt
der Lösung beträgt.
Tabellarische Zusammenstellung der Temperaturgrade, bei
welchen ein Saccharometer die verschiedenen Procentgehalte der
Zuckerlösungen anzeigt, und zwar beim Schwimmen in Lösungen von reinem
Rohrzucker von folgendem Procentgehalte:
Textabbildung Bd. 172, S. 38
Proc.; Temperaturgrade; Angezeigter
Procentgehalt
Diese Tabelle läßt sich in einer anderen Form wiedergeben und zwar in der Weise,
daß man daraus ersieht, wie viel Procente zu dem angezeigten Procentgehalte bei den betreffenden Temperaturen in
Addition oder von ihm in Subtraction zu bringen sind.
Bei folgenden Temperaturen sind zu dem gefundenen Procentgehalte, welchen ein
Saccharometer anzeigt, die in Colonne P angegebenen
Procente in Addition oder von ihm in Subtraction
zu bringen und zwar bei Lösungen von folgendem Procentgehalte:
Textabbildung Bd. 172, S. 39
Bei den Lösungen von folgendem
Zuckergehalt; Procente; Bei folgenden Temperaturgraden nach Celsius; Es sind in
Subtraction zu bringen; Es sind in Addition zu bringen
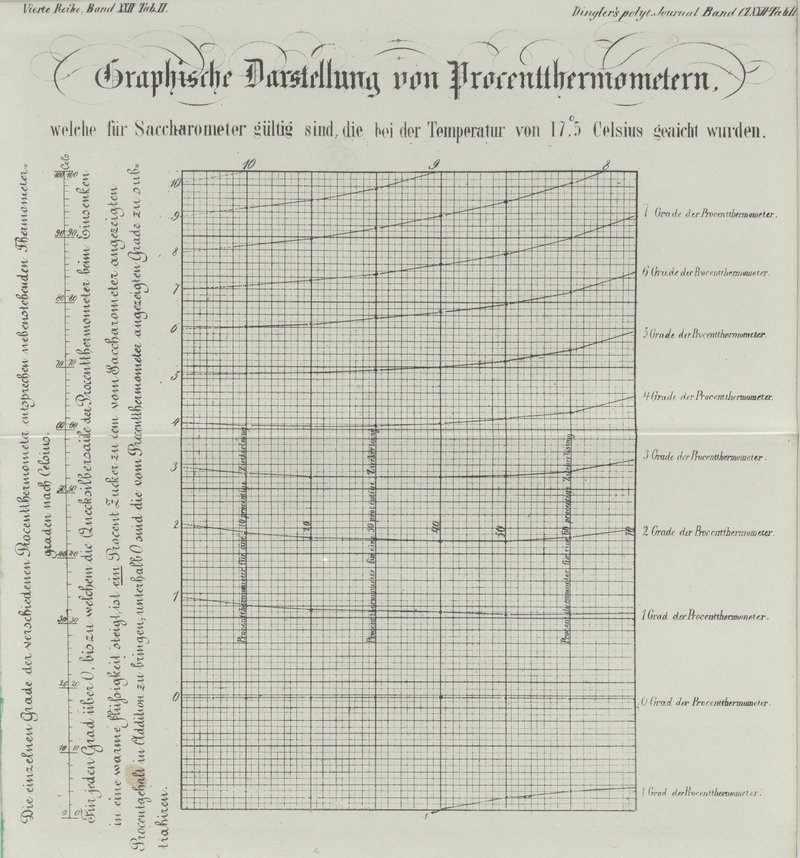
Vergleiche hierüber die auf der lithographirten Tab. II beigegebene graphische Darstellung von Procentthermometern,
welche für Saccharometer gültig sind, die bei der Temperatur von 17°,5 C.
geaicht wurden.
Bringt man in einem Saccharometer ein Thermometer an, in der Weise, daß ein Theil
des Quecksilbers, welches zum Beschweren des Saccharometers dient, gleichzeitig
als Thermometerkugel benutzt wird, so hat man ein sehr bequemes Mittel an der
Hand an der Stelle der Thermometergrade nach Celsius, direct die Anzahl der
Procente zu verzeichnen, welche bei den verschiedenen Temperaturen zu wenig oder
zu viel angezeigt werden, und weil also die einzelnen durch Rechnung gefundenen
Thermometergrade den Procenten an gelöstem Zucker entsprechen, so kann man ein
solches Thermometer Procent-Thermometer
nennen.
Ist das Saccharometer für die Temperatur von 17°,5 geaicht, so hat man
statt der Temperatur 17°,5 bei allen Concentrationsgraden 0
einzuschalten. Wie man aus vorstehender Tabelle ersieht, sind bei den
verschiedenen Concentrationsgraden der Zuckerlösungen die Temperaturen nicht
gleich, bei denen der Procentgehalt um die gleiche Größe zu hoch oder zu niedrig
angegeben wird.
Genau genommen können also nur bei einem bestimmten Procentgehalte die Grade
eines solchen Thermometers einem gewissen Procentgehalte entsprechen, um welchen
das Saccharometer zu hoch oder zu niedrig ergibt; indeß ist es bei der
praktischen Handhabung solcher Instrumente nicht immer genehm in betreffenden
Tabellen die nöthigen Reductionen aufzusuchen und häufig wird es in der Praxis
vorgezogen auf Kosten größerer Genauigkeit schnell ein annähernd richtiges
Resultat zu erhalten.
Bei Alkoholometern ist es ein alter Brauch, selbige mit
Procent-Thermometern zu versehen und man geht hierin sogar oft so weit,
auf einer einzigen Scala sämmtliche Procente von 0 bis 100 Procent zu
verzeichnen und dennoch alle Correcturen nur auf Grund der Angaben eines
einzigen Procent-Thermometers vorzunehmen. Mit bei Weitem größeren
Rechte, mindestens mit demselben Rechte würde man bei Saccharometern denselben
Mißbrauch einführen können. Ich bin jedoch weit davon entfernt, einem solchen
Verfahren das Wort zu reden und halte es für nöthig, wenigstens einen Satz von 3
solchen Saccharometern in Anwendung zu ziehen.
Enthält alsdann
das erste
Saccharometer
die
Procentangaben
von
0 bis 25 Proc.
„ zweite
„
„
„
„
20 bis 50 „
und
„ dritte
„
„
„
„
45 bis 80 „
so wird man einzuschalten haben
in das erste Saccharometer das Procentthermometer für die 10proceentige
Lösung,
in das zweite Saccharometer das Procentthermometer für die 30procentige
Lösung,
in das dritte Saccharometer das Procentthermometer für die 60procentige
Lösung.
Man würde bei der Benutzung dieser Instrumente Resultate erhalten, die nur wenig
von der Wahrheit abweichen und in sehr vielen Fällen dürften sich solche
Saccharometer mit Procent-Thermometern zur praktischen Anwendung
empfehlen.
Indem ich diesen Vorschlag mache, verkenne ich keineswegs, daß solche Instrumente
trügerisch werden können, indem der wenig Geübtere leicht den Irrthum begeht,
die gefundenen Resultate zu überschätzen; nach vorgenommener Correctur auf Grund
der Angaben dieses Thermometers glaubt er den strengsten Anforderungen
vollständig Genüge geleistet zu haben und verfällt somit leicht in eine
Selbsttäuschung.
Bedenkt man aber, daß gewöhnliche käufliche Thermometer oftmals um einen ganzen
Grad, zuweilen sogar um noch mehr von einander abweichen, so wird ein gut
angefertigtes Procentthermometer nach obigen Angaben die Fehler der gewöhnlichen
Thermometer kaum überschreiten.“
––––––––––
Die vorstehende Arbeit bildet wortgetreu einen sehr
wesentlichen Theil einer größeren Abhandlung, welche die Versuche enthält, die der
Verfasser im Auftrage einer von dem Verein für Gewerbfleiß in Preußen und dem Verein
für Rübenzucker-Industrie im Zollverein gemeinschaftlich eingesetzten
Commission ausgeführt hatte.
Diese erwähnte Abhandlung, welche die genaue Feststellung der specifischen Gewichte
von Procent zu Procent und sorgfältig angestellte Versuche über die Ausdehnung der
Zuckerlösungen bei den verschiedenen Concentrationsgraden enthielt, ist nur auszüglich in einem Berichte von dem Hrn. Geheimen
Regierungsrath A. Brix in Berlin, als Mitglied der oben
erwähnten Commission, an anderen Orten veröffentlicht worden und zwar in den
Verhandlungen des Vereins für Gewerbfleiß in Preußen, sowie in der Zeitschrift des
Vereins für Rübenzucker-Industrie im Zollverein. Die vorliegende Arbeit aber
über die Construction von Saccharometern mit dazu gehörenden Procentthermometern
wurde von dem Hrn. Berichterstatter gar nicht, selbst nicht im Auszuge
veröffentlicht; dessenungeachtet hat es demselben beliebt, sich in jenem erwähnten
Berichte in absprechender Weise über die Construction dieser Instrumente öffentlich
auszusprechen und dieser öffentliche Angriff legt mir die Verpflichtung auf, diese
Kritik näher zu beleuchten.
Der Herr Berichterstatter gibt an, daß „das erwähnte Verfahren auf eine Art
von Tatonnement hinauslaufe,“ worauf ich zu erwiedern habe, daß die
Grade der einzelnen Procentthermometer, wie aus der Arbeit ersichtlich ist, durch
Rechnung gefunden sind; und zwar hat die in Anwendung
gezogene Regel (D . d')/d + t = x im vorliegenden Falle vollständig genügende
Berechtigung, weil bei der Interpolation von 5 zu 5 Temperaturgraden die
Abweichungen der Volumenveränderungscurven von der geraden Linie so gering sind, daß
nachweisbar die Angaben keines Aräometers (gleichviel ob Saccharometer oder
Baumé'sche Spindel) dadurch irritirt werden.
Der Hauptvorwurf aber welchen der Herr Geheime Regierungsrath meinen Vorschlägen macht,
besteht darin, daß er angibt, „es sey bei der Reduction der scheinbaren
Procentgehalte unterlassen worden, die Ausdehnung zu berücksichtigen, welche ein
gläsernes Instrument beim Einsenken in eine heiße Zuckerlösung erleide. Der
dadurch bedingte Fehler sey wahrscheinlich größer, als die übrigen Fehler,
vermehre diese jedenfalls beträchtlich genug, um der Abhülfe zu
bedürfen.“ Wenn der Herr Geheime Regierungsrath hierin den
Hauptfehler der Instrumente erblickt, so hoffe ich, daß man bei einer genaueren
Durchsicht der Arbeit, sich von der Irrthümlichkeit dieser Anschauung überzeugen
wird.
Die scheinbaren specifischen Gewichte, welche ich allein
in Betracht gezogen habe, sind gerade solche, wie sie von einem gläsernen
Instrumente beim Einsenken in eine heiße Zuckerlösung direct angezeigt und abgelesen
werden können; was von den scheinbaren specifischen Gewichten gilt, gilt
selbstredend auch von den scheinbaren Procentgehalten der Saccharometer.
Nach dieser Auseinandersetzung halte ich mich für berechtigt, die meinem Verfahren
gemachten Vorwürfe, so wie die hierauf gestützten Folgerungen einfach als
unbegründet zurückzuweisen.
Eines weiteren Eingehens in die gemachten Aeußerungen und ausgesprochenen
persönlichen Ansichten wünsche ich mich enthoben zu sehen, da ich dem sehr geehrten
Herrn Referenten wegen der günstigen Aufnahme meiner übrigen Arbeiten zu Dank
verpflichtet bin.
Bei der großen Bequemlichkeit, welche die Handhabung dieser vorgenannten
Saccharometer bietet, haben dieselben für praktische Zwecke hinreichende
Genauigkeit. Wie sich am besten aus der beigegebenen graphischen Darstellung ersehen
läßt, erreicht der mögliche Irrthum, selbst bei höchst concentrirten Lösungen, sogar
beim Einsenken in sehr heiße Lösungen nie 1/2 Proc., und bei den Lösungen bis 40
Proc. kann man sich selbst im ungünstigsten Falle kaum um
1/5 Proc. irren.
Es wird mir erwünscht seyn, wenn die Herren Industriellen, sowie die betreffenden
Herren Beamten meinem Vorschlage ihre Aufmerksamkeit zuwenden wollten, und ich
bemerke, daß die Firma Ch. F. Geißler in Berlin
(Albrechtstraße Nr. 14) mit der rühmlichst bekannten Sorgfalt mir bereits einen Satz
von drei solcher Saccharometer nach meinen Angaben hergestellt hat. Hr. Geißler berechnet jedes Instrument mit Procentthermometer
und einer Saccharometerscale in 1/5 Procente getheilt, zu 1 1/2 Thlr., oder mit
Cylinder in Etui zu 6 Thlr. Ist die Saccharometerscale nur in 1/2 Procente getheilt,
so vermindert sich der Preis für einen Satz von drei Saccharometern in Etui mit
Cylinder auf 5 1/2 Thaler.
Kalk, bei Cöln a. Rh., den 7. März 1864.
TabelleA., zu Seite 32. – Scheinbare Ausdehnung der Zuckerlösungen bei den verschiedenen
Temperaturen zwischen dem Frostpunkte und dem Siedepunkte in Intervallen von 5
zu 5 Grad Temperaturdifferenz; das Volumen der Zuckerlösungen bei der Temperatur
von 17°,5 Cels. als Einheit.
Textabbildung Bd. 172, Zu S. 42
Temperatur; Procent
TabelleB., zu Seite 34. – Specifische Gewichte der Zuckerlösungen, Wasser von
17°,5 Celsius = 1, bei den
Concentrationsgraden von 5 zu 5 Procent Rohrzucker in 100 Gewichtstheilen der Lösung und bei den Temperaturen von 5
zu 5 Grad zwischen 0 bis 100° Celsius.
Bemerkung: Diese specifischen Gewichte
sind solche, wie sie von gläsernen Scalen-Aräometern, welche für die
Temperatur von 17°,5 C. geaicht wurden, beim Einsenken in die Zuckerlösungen
von verschiedenen Temperaturen, direct angezeigt und abgelesen werden können.
Textabbildung Bd. 172, Zu S. 42
Temperatur; Procent
Tafeln