| Titel: | Ueber die Tragfähigkeit eingerammter Pfähle; von Professor G. Decher. |
| Autor: | Georg Decher [GND] |
| Fundstelle: | Band 173, Jahrgang 1864, Nr. XXXVIII., S. 161 |
| Download: | XML |
XXXVIII.
Ueber die Tragfähigkeit eingerammter Pfähle; von
Professor G. Decher.
Mit einer Abbildung auf Tab. III.
Decher, über die Tragfähigkeit eingerammter Pfähle.
Die theoretische Aufgabe, die Tragfähigkeit eingerammter Pfähle zu bestimmen, besteht
zunächst darin, aus dem Gewichte und der Fallhöhe des Rammklotzes, aus dem Gewicht,
der Länge, dem Querschnitt und dem Elasticitäts-Coefficienten des
eingerammten Pfahles und aus der beobachteten Größe, um welche der Pfahl durch den
letzten Schlag der Ramme (beziehungsweise durch eine sogenannte Hitze von 25 bis 30 Schlägen) eingetrieben wurde, den
Widerstand des Erdreiches gegen das fernere Eindringen des Pfahles zu finden, d. i.
das Gewicht zu berechnen, mit welchem der Pfahl gerade noch belastet werden darf,
ohne daß er dadurch tiefer eingedrückt wird. Dieser Widerstand gibt demnach die
Grenze der Tragfähigkeit des eingerammten Pfahles, und es ist dann Sache der
Erfahrung, zu bestimmen, wie weit man sich dieser Grenze mit einer dauernden und
einer größten vorübergehenden Belastung des Pfahles nähern darf, ohne die Stabilität
des auf denselben gegründeten Baues zu gefährden. Man hat diese Aufgabe schon auf
verschiedene Weise zu lösen versucht, und zwar ohne und mit theilweiser
Berücksichtigung der Beschaffenheit des Pfahlesv. Gerstner, Handbuch der Mechanik, Bd. III; v.
Burg, Compendium der Mechanik und
Maschinenlehre; Prechtl, technologische
Encyklopädie, Bd. XI.; ich fürchte aber nicht, einem Widerspruche zu begegnen, wenn ich auch ohne
eingehende Kritik jener Versuche behaupte, daß dadurch die Theorie von der
Tragfähigkeit eingerammter Pfähle noch keineswegs erschöpft ist, und daß es nicht
ganz ohne Verdienst seyn dürfte, zu dieser Theorie einen neuen Beitrag zu
liefern.
Jene theoretische Aufgabe bietet nämlich unter Zugrundelegung einiger der Wahrheit
ziemlich nahe kommender Voraussetzungen eine gewiß beachtenswerthe Anwendung der im
dritten Buche (Bd. III S. 547 u. ff.) meines Handbuches der Mechanik
vorgetragenen Lehre von der Uebertragung der Bewegung und dem
Stoße, und die daraus hervorgehende Lösung jener Aufgabe dürfte wohl mit
der Natur der Sache viel besser übereinstimmen, als die bisherigen Theorien und die
sich daran anlehnenden praktischen Recepte, welche mit Ausnahme der Theorie v. Burg's schon darin fehlerhaft sind, daß sie keine Grenze
für das Eintreiben des Pfahles in Bezug auf Gewicht und Fallhöhe des Rammklotzes
kennen, sondern den Pfahl bei jeder Größe des Widerstandes durch die kleinste Arbeit
des Rammklotzes eintreiben lassen, wenn auch um eine verhältnißmäßig kleine Größe,
während es auf der Hand liegt, daß bei einer bestimmten Größe des Widerstandes auch
eine bestimmte Arbeit des Rammklotzes erforderlich ist, um diesen Widerstand zu
überwinden, und daß deßhalb dieser Widerstand für gleiche Eintreibung des Pfahles
nicht der Arbeit des Rammklotzes geradezu proportional seyn kann, daß es z.B. nicht
einerlei seyn kann, ob man, wie es die praktische Regel von Burnell im Civil Enginer and Architect's
Journal vorschreibt, einen Pfahl von beliebiger Länge und Schwere mittelst
eines Rammklotzes von 12 Centner bei 4 Fuß Fallhöhe durch 30 Schläge, oder bei 12
Fuß Fallhöhe durch 10 Schläge um 2/5 Zoll eintreibt, ebensowenig als jener
Widerstand oder die Tragfähigkeit des Pfahles bei gleicher Arbeit des Rammklotzes
der Eintreibung des Pfahles proportional ist. Sehr einfach ist meine neue Theorie
allerdings nicht, und es lassen sich die Resultate derselben nicht so geradezu im
Stehen mit Bleistift und Notizbuch berechnen; namentlich wäre die Auflösung der
Aufgabe, wie sie Eingangs ausgesprochen wurde, eine ziemlich schwierige; wir können
aber diese Aufgabe zunächst umgekehrt stellen, wie dieß auch bei den praktischen
Regeln von Woltmann und Burnell geschieht, und sie so aussprechen:
Es ist die für einen beabsichtigten Bau nothwendige Belastung
eines Pfahles und damit der kleinste Widerstand des Erdreiches gegen das tiefere
Eindringen des Pfahles gegeben; es soll bestimmt werden, wie viel der Pfahl durch
den letzten Schlag (bez. eine Hitze von 25 oder 30 Schlägen) eines Rammklotzes von
bestimmtem Gewicht und bei gegebener Fallhöhe desselben noch eingetrieben werden
darf, damit dieser Widerstand erreicht ist,
und meine Theorie läßt sich sowohl in dieser als in der
ursprünglichen Fassung der Aufgabe dem Praktiker durch Tabellen (wie die am Schlusse
beigefügte) zugänglich machen, in welchen für die in der Anwendung am meisten
vorkommenden Arten von Rammblock-Gewichten und Fallhöhen und die entsprechende Stärke der
Pfähle die Eintreibungen dieser letzteren bei verschiedenen Widerständen des
Erdreiches berechnet sind.
Die Voraussetzungen, welche ich meiner Theorie zu Grunde lege, sind folgende:
1) Der Widerstand gegen das Eindringen des Pfahles bleibt für die Dauer des letzten
Schlages der Ramme (bezüglich der letzten Hitze) constant;
2) dieser Widerstand kann in dem unteren Ende des Pfahles vereinigt angenommen
werden, d.h. der an den Seiten des Pfahles wirkende Widerstand hat keinen oder einen
zu vernachlässigenden Einfluß auf das Gesetz, nach welchem der Pfahl durch den auf
seinen Kopf ausgeübten Druck gestaut oder verkürzt wird;
3) diese Verkürzung des Pfahles ist dem auf seinen Kopf durch den Stoß des
Rammklotzes ausgeübten Drucke und seiner Länge direct und seinem mittleren
Querschnitt und Elasticitäts-Modul verkehrt proportional;
4) der Pfahl ist aber nicht vollkommen elastisch; er dehnt sich nach der größten
Verkürzung in der zweiten Hälfte des Stoßes nicht gerade so wieder aus, wie er
gestaut worden ist, sondern weniger, und behält am Ende des Stoßes noch eine kleine,
erst allmählich wieder verschwindende Verkürzung; bei dieser Ausdehnung des Pfahles
bleibt aber die Voraussetzung 3) bestehen, nur mit dem Unterschiede, daß für diese
zweite Hälfte des Stoßes der Elasticitäts-Modul ein größerer ist (vergl. mein
Handbuch der Mechanik, Bd. III S. 563 u. ff.); endlich
5) es kann von der unbedeutenden Compression und Extension des Rammklotzes der
Einfachheit wegen Umgang genommen werden.
Es sey nun
das Gewicht des Rammklotzes
= Q,
die Fallhöhe desselben
= H,
die Beschleunigung des Falles
= g,
das Gewicht des Pfahles
= P,
die Länge desselben
= L,
sein mittlerer Querschnitt
= a²,
sein Elasticitäts-Modul oder -Coefficient
= E,
der vom Rammklotz auf den Pfahl ausgeübte
augenblickliche Druck
= N,
die durch diesen Druck bewirkte augenblickliche
Verkürzung des Pfahles während der
ersten Hälfte des Stoßes
= l,
die sehr kleine bleibende Verkürzung desselben am Ende
des Stoßes L
– L'
= αL,
die dem Drucke N entsprechende
augenblickliche Verkürzung in der
zweiten Hälfte des Stoßes
= l',
der entsprechende Elasticitäts-Coefficient
= E',
der constante Widerstand des Erdreichs
= W;
man hat dann zunächst nach Voraussetzung 3) in der ersten
Hälfte des Stoßes zwischen der Verkürzung l und dem
Druck N die Beziehung:
l/L = N/Ea², l = L
N/Ea², (1.
und ebenso zwischen l' und N in der zweiten Hälfte
l'/L' = N/E'a², l' =
L'
N/E'a², (2.
Ist dann Nm der am
Ende der ersten Hälfte des Stoßes eintretende größte Werth von N, und lm die entsprechende Verkürzung des Pfahles,
so wird l'm die
Größe seyn, um welche sich dieser in der zweiten Hälfte des Stoßes wieder ausdehnt,
und man hat als bleibende Verkürzung am Ende des Stoßes
L – L' = αL = lm – l'm
= L Nm/Ea² – L' Nm/E'a²;
daraus ergibt sich die Beziehung:
Textabbildung Bd. 173, S. 164
woraus mit hinreichender Annäherung
E' = E/μ² (3b).
folgt, indem man die kleine Größe α neben 1 vernachlässigt und den Factor 1 – (L – L')/lm, welcher
jedenfalls ein ächter Bruch ist, da die bleibende Verkürzung L – L' des Pfahles immer kleiner seyn
muß als die größte Verkürzung lm, durch μ² ersetzt. Man wird auch leicht erkennen, daß die Grenzwerthe
μ² = 0 und μ² = 1 den Voraussetzungen eines durchaus unelastischen und
eines vollkommen elastischen Pfahles entsprechen, da im ersten Falle die größte
Stauung auch die bleibende, und im zweiten Falle L'
wieder gleich L ist. Diese Beziehung (3) würde dazu
dienen, aus den: beobachteten Werthe von L – L'
den von μ zu berechnen, wenn jene Größe mit
genügender Sicherheit beobachtet werden könnte. Da es aber dazu kaum ein Mittel
geben dürfte, so möchte es wohl am einfachsten und zweckmäßigsten seyn, den Werth
von μ, wie es a. a. O. meines Handbuches
angegeben ist, dadurch zu bestimmen, daß man einen kürzeren Pfahl aus demselben
Holze wie die einzutreibenden auf eine feste Unterlage aufsetzt, den Rammklotz auf
denselben fallen läßt und die Höhe beobachtet, bis zu welcher derselbe nach dem
Stoße wieder aufspringt; man hat dann, wenn diese letztere Höhe mit h bezeichnet wird,
2 gh = μ² . 2 gH,
μ = √(h/H). (4.
Führen wir dann den Werth (3ª) von E' in die Gleichung (2) ein, so
gibt diese mit dem aus (3b) folgenden
Werthe von μ² den Werth von l' in der einfachen Form:
l' = μ²L N/Ea² =
μ²l. (5.
Wir nehmen nun die verticale Achse des Pfahles, in welcher auch der Schwerpunkt des
Rammblockes liegen soll, als z-Achse an, verlegen
den Anfangspunkt der z in das untere Ende des Pfahles
vor dem Beginn des letzten Schlages, von dem an auch die Zeit t gezählt werde, rechnen die positiven z nach
unten und bezeichnen für das Ende dieser Zeit t mit
z die Eintreibung der Pfahlspitze d. i. ihren Abstand
von jenem Anfangspunkte der z, mit
z' den Abstand des Schwerpunktes der Ramme von demselben
Punkte und mit
v und v' die
Geschwindigkeiten der Pfahlspitze und dieses Schwerpunktes; ferner mit
– c' den Werth von z' am Anfang der Zeit t.
Wir haben dann für die Bewegung des Rammklotzes
(beziehungsweise seines Schwerpunktes) während des letzten Schlages von dem
Augenblicke an, wo der Rammblock den Pfahl zu berühren anfängt, die Gleichungen:
Q/g dv'/dt = Q – N, v' = dz'/dt; (6.
die Bewegung der Pfahlspitze, in welcher wir nach
Voraussetzung (2) und weil es sich nur um eine geradlinige fortschreitende Bewegung
handelt, die Masse des Pfahles vereinigt annehmen können, wird durch die
Gleichungen:
P/g dv/dt = N + P – W,
v = dz/dt (7.
dargestellt, und für die Verkürzungen l und l' des Pfahles ergeben sich die
Beziehungen:
l = L N/Ea²
= c' – (z
– z'),l'
= μ²L
N/Ea² = c' – αL – (z – z')
(8.
und unsere Aufgabe besteht nun darin, aus diesen Gleichungen
durch Elimination von N und z' die Eintreibung z der Pfahlspitze für das
Ende des letzten Schlages durch die Gegebenen ausgedrückt abzuleiten.
Um diese Aufgabe richtig zu lösen, müssen wir aber in der kurzen Dauer dieses letzten
Schlages oder Stoßes außer dem Hauptabschnitt zwischen der ersten und zweiten Hälfte
desselben noch einige weitere Zeitabschnitte machen, weil auch in jeder dieser
Hälften die Pfahlspitze noch wesentlich verschiedene Bewegungszustände besitzt oder
besitzen kann. Denn
1) leuchtet ein, daß sich die Pfahlspitze nicht bewegen kann, so lange das Gewicht
des Pfahles und der Druck auf denselben zusammen noch kleiner sind als der
Widerstand des Erdreiches; unser erster Zeitabschnitt wird also vom Anfang des
Stoßes, wo N = 0 ist, bis zu dem Augenblicke reichen, wo
N + P = W geworden, und während dieses Zeitabschnittes wird die
Pfahlspitze unbewegt bleiben.
2) Sobald aber N die obengenannte Größe erreicht hat und
sie überschreitet, wird die Pfahlspitze eine beschleunigte Bewegung annehmen, und
diese wird gleichartig fortdauern, bis N und l ihre größten Werthe erreicht haben, mit welchen unser
zweiter Zeitabschnitt und die erste Hälfte der Dauer des Stoßes schließt.
3) Von diesem Zeitpunkte an wird N wieder kleiner und
steht in einer anderen Beziehung zu der Compression des Pfahles, durch welche der
Factor μ in die Bewegungsgleichungen eingeführt
und eine neue Aufstellung dieser Gleichungen nothwendig wird; die daraus
hervorgehende Bewegung bleibt jedenfalls gleichartig, bis wieder N + P = W geworden ist, und wenn es auch nicht geradezu
nothwendig ist, so dürfte es doch sehr die Auffassung erleichtern, wenn wir mit
diesem Zeitpunkt unseren dritten Zeitabschnitt schließen.
4) Mit dem Anfang des vierten Zeitabschnittes wird die Bewegung der Pfahlspitze
nothwendig eine verzögerte, und es können nun je nach der Größe von W in Bezug auf P, Q und H zwei Fälle eintreten;
a) entweder ist die Verzögerung dieser Bewegung so groß,
daß die Geschwindigkeit der Pfahlspitze eher Null wird, als der Druck N auf den Pfahl; dann bleibt sie von da an Null, und die
Bewegung der Pfahlspitze erreicht mit dem vierten Zeitabschnitt ihr Ende, oder
b) es wird N eher Null als
die Geschwindigkeit der Pfahlspitze; dann schließt der vierte Zeitabschnitt mit N = 0, und es folgt noch ein fünfter, in welchem die
Pfahlspitze durch die ihrer Geschwindigkeit entgegenwirkende constante Kraft W – P eine
gleichförmig verzögerte Bewegung annimmt und diese mit der Geschwindigkeit Null
beschließt.
Um diese verschiedenen Zeitabschnitte auch in den Gleichungen anzudeuten, wollen wir die Veränderliche t selbst sowie die von ihr abhängigen Veränderlichen N, N' = dN/dt, v und z je nach der Ordnungszahl des betreffenden
Zeitabschnittes mit dem Index 1, 2, 3 etc. versehen, und dann noch die besonderen
Werthe dieser Veränderlichen für das Ende dieser Zeitabschnitte mit deutschen
Buchstaben t, N, N', v, z und dem entsprechenden Index
bezeichnen.
Erster Zeitabschnitt.
Der erste Zeitabschnitt beginnt in dem Augenblick, wo der Rammklotz den Pfahl
berührt, also l und folglich nach (1) auch N = 0 ist, und der Schwerpunkt des Rammklotzes sich
durch den Fall von der Höhe H die Geschwindigkeit:
v'₀ = √2gH
erworben hat. Die Pfahlspitze bleibt in diesem ganzen
Zeitabschnitt ohne Bewegung, also z = 0, weil immer W > N + P, und die erste der
Beziehungen (8) kommt auf
l = L
N₁/Ea² = c' + z₁'
zurück, woraus
v₁' = dz₁'/dt₁ = L/Ea² dN₁/dt₁, dv₁'/dt₁ = L/Ea² dN₁'/dt₁ (9.
folgt und sich durch Elimination von dv₁'/dt₁ mittelst der Gleichung
(6) für N₁ die charakteristische Gleichung:
dN₁/dt₁ = g Ea²/LQ (Q – N₁) (10.
ergibt. Beachtet man dann, daß L
Q/Ea² nach (1) die Verkürzung λ
ausdrückt, welche der einzurammende Pfahl durch den Druck oder das daraufliegende
Gewicht Q erleiden würde, so nimmt das unbestimmte
Integral der Gleichung (10) die Form an:
Textabbildung Bd. 173, S. 167
worin A₁ und B₁ die noch zu bestimmenden Constanten der
Integration bedeuten. Man hat dann auch
Textabbildung Bd. 173, S. 167
und die Bedingungen:
t₁ = 0, N₁ = 0, N₁' = Ea²/L v₀' =
Ea²/L
√(2gH) = Q
√(2gH)/λ;
daraus folgen die Werthe:
A₁ = Q, B₁ =
– Q √(2H/λ)
und die allgemeinen Beziehungen:
Textabbildung Bd. 173, S. 168
Dieser erste Zeitabschnitt ist zu Ende, wenn N = W – P geworden ist;
seine Dauer t₁ bestimmt sich daher durch die
Bedingung:
Textabbildung Bd. 173, S. 168
oder wenn man
Textabbildung Bd. 173, S. 168
setzt, durch die Bedingung:
Φ cos β = sin (β + τ₁ – π/2), (12.
und für das Ende dieses Zeitabschnittes und den Anfang des
folgenden hat man demnach die besondern Werthe:
Textabbildung Bd. 173, S. 168
Aus (12) zieht man als größte Dauer des ersten
Zeitabschnittes
Textabbildung Bd. 173, S. 168
und diese tritt ein, wenn Φ cos
β = 1 ist; damit wird aber der letzte Werth (13): N₁' = 0 und spricht
aus, daß dann N schon am Ende des ersten Zeitabschnittes
seinen größten Werth Nm erreicht, daß also mit dem ersten auch schon der zweite Zeitabschnitt zu
Ende ist, und daß, weil mit dem dritten Zeitabschnitt N
wieder kleiner wird, v und z
immer Null bleiben, also keine Bewegung der Pfahlspitze eintritt. Noch weniger ist
dieses der Fall, wenn Φ cos β > 1, weil
dann τ₁ und N₁' imaginär werden, N also niemals den Werth W
– P erreichen kann. Die Forderung, daß sich die
Pfahlspitze bewegen soll, ist demnach an die Bedingung:
Φ < sec
β geknüpft, welche mit den frühern Werthen in
1 + 2H/λ > Φ², H >
½ λ (Φ² – 1) (14.
übergeht, und so die kleinste Fallhöhe H für einen Rammklotz von gegebenem Gewicht Q
bestimmt, wenn durch diesen ein Pfahl von gegebener physischer und geometrischer
Beschaffenheit bei einem gegebenen Widerstande W des
Erdreiches noch um etwas eingetrieben werden soll.
Ist dieser Widerstand W gegen die Gewichte P und Q sehr groß, so daß
man 1 neben Φ² vernachlässigen kann, so
hat man mit Einführung des Werthes von λ
Textabbildung Bd. 173, S. 169
und wenn man noch P und Q neben W vernachlässigt,
was um so mehr zulässig ist, als man in der Anwendung doch nicht bis an die Grenze
gehen kann, so wird einfacher
QH > ½ L W²/Ea² (15b.
die erste zu erfüllende Bedingung zwischen der Arbeit des
Rammklotzes, der Länge und Elasticität des Pfahles und dem Widerstand, den das
Erdreich gegen das tiefere Eindringen desselben leisten soll, und man schließt
daraus, daß jene Arbeit des Rammklotzes dem Quadrat des
Widerstandes oder dem Quadrat der theoretischen Tragfähigkeit des Pfahles, sowie
der Länge und Zusammendrückbarkeit des letztern proportional seyn muß.
Aus der Bedingung (15b) würde man übrigens
auch eine sehr einfache Beziehung für die Tragfähigkeit eines Pfahles erhalten, wenn
man das Einrammen so lange fortsetzen wollte oder könnte, bis der Pfahl nicht mehr
weiter eindringt; denn in diesem Falle hätte man
Textabbildung Bd. 173, S. 169
es leuchtet aber ein, daß ein solches Verfahren für die Praxis
viel zu zeitraubend wäre, um ernstlich empfohlen werden zu können.
Zweiter Zeitabschnitt.
Der zweite Zeitabschnitt beginnt mit N = W – P = Q (Φ + 1) und endigt
mit dem größten Werthe von N oder mit N' = 0. In diesem Zeitraum bestehen die Gleichungen (6)
und (7) und die erste der Gleichungen (8) zusammen; aus den beiden ersten folgt
dv'₂/dt₂ – dv₂/dt₂ = g[W/P – N₂(1/P + 1/Q)], (17.
und daraus geht mittelst des zweiten Aenderungsgesetzes jener
ersten Gl. (8) in Bezug auf t nämlich
dv₂'/dt₂ – dv₂/dt₂ = L/Ea₂ dN₂'/dt₂ = λ/Q dN₂'/dt₂,
für N₂ die
charakteristische Gleichung:
dN₂/dt₂ = g/λ (νW – (1 + ν)N₂) (18.
hervor, worin wieder LQ/Ea₂ durch λ,
und Q/P durch v ersetzt
ist.
Das unbestimmte Integral dieser Gleichung ist
N₂ = ν/(1 + ν) W + A₂ cos
γt₂ + B₂ sin
γt₂, (19.
wenn noch zur weiteren Abkürzung der Factor durch γ ersetzt wird, und für die beiden unbestimmten
Constanten A₂ und B₂ ergeben sich durch das Aenderungsgesetz dieses Integrales in Bezug
auf t, nämlich
dN₂/dt₂ = γ(B₂ cos γt₂ – A₂ sin
γt₂) = N₂',
und die Werthe (13) von N₁
und N₁', welche auch die von N₂ und N₂' für t₂ = 0 sind,
die bestimmten Werthe:
Textabbildung Bd. 173, S. 170
und damit hat man, weil W = QΦ + Q + P = Q(1 + Φ + 1/v) ist
Textabbildung Bd. 173, S. 170
Der zweite Zeitabschnitt ist zu Ende, wenn N₂' = 0 geworden ist, und die letzte Gleichung gibt damit
für die Dauer t₂ dieses Zeitabschnittes die
Beziehung:
Textabbildung Bd. 173, S. 170
und der entsprechende größte Werth von N wird
Textabbildung Bd. 173, S. 170
Führen wir nun den Werth (20) von N₂ in die erste
Gleichung (7) ein, so nimmt diese mit dem obigen Werthe von W – P die Form an:
Textabbildung Bd. 173, S. 171
und gibt, wenn man noch die Gleichung (21) beachtet,
Textabbildung Bd. 173, S. 171
Man zieht daraus durch die erste Integration für die Geschwindigkeit der
Pfahlspitze
Textabbildung Bd. 173, S. 171
und die nochmalige Integration gibt für die Eintreibung
derselben
Textabbildung Bd. 173, S. 171
da man hat g/γ² =
λ/(1 + v), und
man wird leicht erkennen, daß man darin für das Ende des zweiten Abschnittes nur
γt₂ = τ₂ für γt₂ setzen
darf, um die Werthe von v₂ und z₂ zu erhalten; diese werden demnach
Textabbildung Bd. 173, S. 171
und sind zugleich die anfänglichen Werthe von v und z für den dritten
Zeitabschnitt. Alle diese Werthe zeigen nun augenfällig, daß mit der Bedingung: Φ cos β = 1 die Dauer t₂ des zweiten Zeitabschnittes Null wird und daß
auch v₂ und z₂
wie v₁ und z₁
Null bleiben, die Pfahlspitze also nicht tiefer eindringt.
Dritter Zeitabschnitt.
Im dritten Zeitabschnitt, welcher mit N = Nm beginnt und den ich der einfacheren
Betrachtung wegen mit N = W
– P schließe, obgleich er dadurch nicht
nothwendig begrenzt ist, kommt statt der ersten die zweite der Gleichungen (8) zur
Anwendung, und man zieht daraus
dv'₃/dt₃ – dv₃/dt₃ = μ² L/Ea₂ dN₃'/dt₃ = μ² λ/Q dN'₃/dt₃,
Die Gleichung (17) des vorigen Abschnittes besteht noch fort
und führt mit der vorstehenden verbunden auf
Textabbildung Bd. 173, S. 171
welche sich von der Gl. (18) nur durch den Factor μ² vor λ unterscheidet; man erhält daher jetzt für das unbestimmte Integral und
dessen Ableitung
Textabbildung Bd. 173, S. 172
und mit den Werthen (22) von N₂ und N'₂ = 0 folgt
Textabbildung Bd. 173, S. 172
also auch
Textabbildung Bd. 173, S. 172
Die letzte dieser Gleichungen zeigt, daß im dritten Zeitabschnitt N wieder im Abnehmen begriffen ist, und die erste gibt
durch die Bedingung N₃ = W – P = Q
(Φ + 1) für die Dauer t₃ dieses Zeitabschnittes die Beziehung:
γt₃/μ = τ₂
= γt₂, t₃ = μ
t₂, (27.
womit dann weiter für das Ende desselben
Textabbildung Bd. 173, S. 172
folgt. Durch die Gleichung (7) erhält man dann wieder mittelst
der ersten Gl. (26) die Beziehung:
Textabbildung Bd. 173, S. 172
und zieht daraus nach und nach die Werthe:
Textabbildung Bd. 173, S. 172
Für das Ende des dritten Zeitabschnittes hat man der Beziehung (27) zufolge dv₃/dt₃ = 0;
es hat also die Geschwindigkeit der Pfahlspitze am Ende dieses Zeitabschnittes ihren
größten Werth erreicht und dieser ist
Textabbildung Bd. 173, S. 172
ferner ergibt sich
Textabbildung Bd. 173, S. 173
oder mit den Werthen von v₂
und t₂ und nach einigen weiteren Reductionen
Textabbildung Bd. 173, S. 173
und diese Werthe (29) und (30) bestimmen wieder mit (28) und
dem von N₃ den anfänglichen Zustand des Pfahles
für den nächsten Zeitabschnitt.
Vierter Zeitabschnitt.
Der vierte Zeitabschnitt endigt entweder mit v₄ =
0 oder N₄ = 0, je nachdem das eine oder andere
zuerst eintritt; die Gleichungen (25) bestehen mit neuem Index sonst unverändert
fort, geben aber mit den anfänglichen Werthen N₃
und N'₃ von N₄
und N'₄
Textabbildung Bd. 173, S. 173
und damit werden die allgemeinen Werthe von N und N' für diesen
Zeitraum
Textabbildung Bd. 173, S. 173
Mit dem ersten dieser Werthe folgt sodann
Textabbildung Bd. 173, S. 173
und die erste Integration in Bezug auf t₄ gibt, γt₄/μ = τ₄
gesetzt, für v₄ den Werth:
Textabbildung Bd. 173, S. 173
welchem man man mit den Werthen von v₃ und v₂ die Form geben
kann:
Textabbildung Bd. 173, S. 173
Soll demnach mit diesem vierten Zeitabschnitt auch die Bewegung der Pfahlspitze
endigen, so muß man haben
v₄ = 0 = tang τ₂ – τ₂ + μ sin (τ₂ + τ₄) sec τ₂ –
μ (τ₂ + τ₄), (34.
ohne daß N₄ mit dem daraus
folgenden Werthe von τ₄ negativ wird. Das
Letztere würde der Fall seyn, wenn der aus der ersten Gleichung (31) mit der
Bedingung N₄ = N₄ = 0 folgende Werth von
$#x03C4;₄ kleiner wäre, als der aus (34)
folgende, und in diesem Falle würde der vierte Zeitabschnitt mit N₄ = 0
schließen und noch ein fünfter mit einer gleichförmig verzögerten Bewegung der
Pfahlspitze folgen. Es ist daher vor Allem zu untersuchen, unter welchen
Verhältnissen der eine und unter welchen der andere Fall eintritt.
Die erste Gleichung (31) gibt mit der Bedingung N₄ = 0 und der schon
angewendeten Bezeichnung
tang τ₂ sin τ₄ – cos
τ₄ = (1 + v + vΦ)/Φ
oder
cos (τ₂ + τ₄) =
– (1 + v + vΦ)/Φ cos
τ₂; (35.
diese Bedingung ist demnach von μ ganz unabhängig. Für die in der Anwendung vorkommenden
Verhältnisse ist aber meistens v wenig von 1 verschieden
und vΦ viel größer als 1 + v; man kann deßhalb in erster Annäherung und für die Anwendung meistens
hinreichend genau
cos (τ₂ + τ₄) =
– cos τ₂, τ₄ = π – 2τ₂
(36.
als den Werth von τ₄
nehmen, mit welchem N₄ Null wird. Dieser Werth von τ₄ wird demnach offenbar um so größer, je kleiner τ₂ ist, je mehr sich also der Werth von
Φ seiner Grenze sec
β nähert, oder je größer der Widerstand W gegen das Eindringen des Pfahles im Verhältniß zu der Arbeit des
Kammklotzes ist, und umgekehrt um so kleiner, je größer τ₂ wird, und man hat für die den beiden Grenzwerthen von τ₂, welche den Werthen Φ = 0 und Φ =
sec β entsprechen, zugehörigen Werthe von τ₄
Φ = 0, τ₂ = π/2, τ₄ = 0; Φ = sec β, τ₂ = 0,
τ₄ = π.
Gerade umgekehrt verhält es sich mit dem aus Gl. (34) folgenden Werthe von τ₄; denn diese Gleichung unter die
Form:
τ₂ + τ₄ – sec
τ₂ sin (τ₂ + τ₄) = 1/μ (tang
τ₂ – τ₂) (37.
gebracht, zeigt daß für ein und denselben Werth von μ der Werth von τ₄ mit dem von τ₂
wächst und abnimmt; denn man findet für τ₂
= 0 und für jeden Werth von μ = 0 bis μ = 1 auch τ₄ = 0; für τ₂ = π/4 wird die Bedingung (37)
τ₄ – sin τ₄ – cos τ₄ = 1/μ (1 – π/4) – π/4
und läßt sich in zwei zerlegen, je nachdem μ ≶ (4 – π)/π oder ≶ 0,2732 also
μ² ≶ 0,07466; im ersten Falle
ist τ₄ kleiner, im zweiten größer als
72° 10', erhält aber für den größten Werth μ = 1 noch den Werth 48° 12', und wird für μ = 0 unendlich u.s.f.
Es muß demnach zwischen den beiden Grenzwerthen von τ₂ und für einen bestimmten Werth von μ immer einen solchen Werth von τ₄ geben, welcher den beiden Bedingungen (36) und (37)
gleichzeitig Genüge leistet, für welchen also N und v gleichzeitig Null werden, und wenn man aus diesen
Bedingungen das τ₄ eliminirt, so wird man
eine Gleichung in τ₂ und μ erhalten, oder unter Anwendung der strengeren
Bedingung (35) in τ₂ μ und v, aus welcher
der Werth von τ₂, und mit BeziehungBeiziehung der Gl. (21) das Verhältniß von Φ und
sec β abgeleitet werden kann, für welches das
gleichzeitige Nullwerden von N und v statt hat, welches also die Grenze bildet für die
Fälle, in denen N vor v und
in denen v vor N Null wird.
Die beiden Bedingungen (36) und (37) führen auf die ziemlich einfache Gleichung:
(1 + μ) tang τ₂ – (1 – μ) τ₂ = μπ, (38.
und diese gibt für μ = 1,
tang τ₂ = π/2, τ₂ = 57°31',
für μ = 0, τ₂ = 0; es muß demnach und zufolge der Gl. (21), welche nach Φ aufgelöst den Ausdruck:
Textabbildung Bd. 173, S. 175
gibt, und wenn darin v = 1 gesetzt
wird, Φ zwischen oder nahe 2/3 sec β und sec
β liegen, wenn für alle Werthe von μ zwischen 1 und 0 die Geschwindigkeit v vor N Null werden, die Bewegung der
Pfahlspitze also mit dem vierten Zeitabschnitt endigen soll.
Für die in der Anwendung vorkommenden Materialien lassen sich aber die Grenzen von
μ viel enger ziehen und auf 1/3 und 2/3 fest
setzen, wo durch μ² zwischen 1/9 und 4/9
beschränkt wird, und diese Werthe des Verhältnisses h :
H der Gleichung (4) genügen offenbar der Erfahrung.
Führen wir dann die Werthe μ = 1/3 und μ = 2/3 in die Gl. (38) und die sich ergebenden
τ₂ in (39) ein, so wird:
μ = 1/3, 4 tang τ₂ – τ₂ = π, τ₂
= 50°52', Φ = 0,755 sec β,
μ = 2/3, 5 tang τ₂ – τ₂ = 2π, τ₂
= 55°24', Φ = 0,698 sec β.
Um nun aber auch den Einfluß von v auf die eben bestimmte
Grenze kennen zu lernen, wollen wir auch die Gleichung (35) mit (37) verbinden, aber
in der etwas vereinfachten Form:
cos (τ₂ + τ₄) =
– v cos τ₂, τ₂ + τ₄ = π – ang cos
(v cos τ₂),
in welcher noch 1 + v neben v Φ vernachlässigt ist, aus welcher dann
sin (τ₂ + τ₄) =
√(1 – ν²cos²τ₂)
folgt und die mit (37) auf die Bedingungsgleichung
führt: (40.
μπ = μ ang cos (ν cos
τ₂) + μ sec
τ₂ √(1 – ν² cos²τ₂) + tang τ₂
– τ₂.
In diese Gleichung wollen wir dann neben den oben
festgesetzten Grenzwerthen von μ auch zwei für
die Anwendung zulässige Grenzwerthe von v (als welche
v = 2 für P = 1/2 Q und v = 1/2 für P = 2 Q anzunehmen genügen
dürfte) einführen, und werden damit und mit den früheren Ergebnissen für τ₂ und Φ folgende Werthe finden:
μ
= 1/3,
v
= 1/2,
τ₂
= 44°36',
Φ cos β
= 0,775..,
= 1,
= 50 52,
= 0,754..,
= 2,
= 61 19,
= 0,687..,
μ
= 2/3,
v
= 1/2,
τ₂
= 49°16',
Φ cos β
= 0,725..,
= 1,
= 55 24,
= 0,698..,
= 2,
= 64 24,
= 0,638..,
Diese Tabelle dürfte hinreichen, um für alle in der Anwendung
vorkommenden Fälle schon von vorn herein zu erkennen, ob die Bewegung der
Pfahlspitze mit dem vierten Zeitabschnitt endet oder nicht.
Integriren wir nun das erste Integral der Gleichung (32) noch einmal und setzen den
Werth von v₃ ein, so erhalten wir als Eintreibung
der Pfahlspitze am Ende des vierten Zeitabschnittes oder nach der Zeit t₄ = (μ/γ) τ₄
Textabbildung Bd. 173, S. 176
und man hat in diesen Ausdruck für τ₄ entweder den aus Gl. (34) oder den aus Gl. (35) folgenden
Werth einzuführen, je nachdem der vierte Zeitabschnitt mit v₄ = 0 oder mit N₄ = 0 endigt.
Fünfter Zeitabschnitt.
Wenn der vierte Zeitabschnitt mit N₄ = 0 endigt, ohne daß v₄ = 0 ist, so bewegt sich die Pfahlspitze nach
dem Ende dieses Zeitabschnittes noch eine kurze Zeit t₅ fort, und zwar mit einer gleichförmig verzögerten Bewegung, deren
Gleichungen sind:
Textabbildung Bd. 173, S. 177
und welche demnach mit den Werthen:
Textabbildung Bd. 173, S. 177
ihr Ende erreichen muß.
Anwendungen.
Mit diesen letzten Ergebnissen hat unsere Aufgabe ihre vollständige Lösung gefunden,
indem entweder z₄ oder z₅ die ganze Eintreibung des Pfahles durch einen Schlag der Ramme
angibt, je nachdem die fortschreitende Bewegung des Pfahles mit dem vierten oder
fünften Zeitabschnitt endet.
Es erübrigt uns demnach noch, von unserer Untersuchung und den entwickelten Formeln
einige Anwendungen zu machen. Dazu und um die verwickelte Beziehung zwischen der
Arbeit des Rammklotzes, der Größe des Widerstandes und der Eintreibung des Pfahles
leichter durchschauen zu können, wollen wir jene Beziehungen für zwei Rammen
berechnen, durch welche die Fallhöhen H = 1,8 und = 3,6
Meter erzielt werden können, und bei deren jeder 2 Rammblöcke von 300 und 600
Kilogr. Gewicht zur Anwendung kommen, so daß wir folgende drei Arbeitsgrößen
erhalten:
QH
= 300 × 1,8 =
540
Meter
Klgr.
,
= 600 × 1,8 =
300 × 3,6 =
1080
„
„
,
= 600 × 3,6 =
2160
„
„
.
Daraus berechnet sich der größte Widerstand Wm, welcher noch mit dieser Arbeit bewältigt
werden kann, nach der einfachen Gleichung (15):
LWm² = 2 QH .
Ea² (43.
wenn die Länge L und der
Querschnitt a² des Pfahles bestimmt sind. Diese
Größen stehen aber auch in nothwendigem Zusammenhang mit der Tragfähigkeit des
Pfahles; wir müssen also, ehe wir weiter rechnen, noch Beziehungen für die
ebengenannten Größen aufstellen.
Für diese Beziehungen gehe ich von der Annahme aus,
1) daß die durch die Belastung des Pfahles erzeugte Stauung die sogenannte
Elasticitätsgrenze nicht überschreiten soll, d.h. diejenige Größe der relativen
Stauung, bei welcher eine auch nach Wegnahme der Belastung noch fortdauernde
Einwirkung fühlbar zu werden anfängt, daß demnach die Beziehung:
Wm = δ
Ea² (44.
besteht, in welcher δ ein
jene Grenze bestimmender Bruch ist;
2) daß die Länge des Pfahles nur drei Viertel derjenigen Länge seyn soll, welche
derselbe mit dem Querschnitt a² und dem
Biegungsmoment B erhalten darf, damit er ganz
freistehend unter der Belastung Wm, nur eine einfache Biegung annehmen kann,
also 3/4 der Länge, welche sich aus der Beziehung L²
Wm = π
²B
ergibt, so daß man auch die Gleichung hat:
L²Wm = 9/16 π
²
B; (45.
3) daß der Querschnitt des Pfahles, wenn auch nicht genau ein Kreis oder ein Quadrat,
doch eine diesen nahekommende Figur ist und daher
B = 0,08 Ea⁴ (46.
genommen werden kann.Für ein Quadrat hat man bekanntlich B = 1/12 Ea⁴, für einen Kreis B = 1/4 πr⁴; macht man aber πr² = a², so wird
für letzteren, wenig abweichend von jenem, B =
1/(4π) a⁴ = 1/12,56 a⁴. Die Gleichung (44) gibt dann den Werth von a² und damit und mit (46) folgt aus (45) der Werth von L, für welchen man mit hinreichender Genauigkeit π² = 10 und
Textabbildung Bd. 173, S. 178
nehmen kann, und welcher zeigt, daß unter den obigen Annahmen
die Länge L in einem constanten Verhältniß zu der
mittleren Dicke a des Pfahles steht, übereinstimmend mit
den von Woltmann angenommenen Normal-Pfählen (Prechtl's technologische Encyklopädie Bd. XI). Führt man
nun die aus (44) und (47) folgenden Werthe von a²
und L in die Gleichung (43) ein, so zieht man daraus
Textabbildung Bd. 173, S. 178
zuletzt findet man noch für das Gewicht des Pfahles den
Werth:
Textabbildung Bd. 173, S. 178
worin p das Gewicht der
Volumen-Einheit des Pfahles bezeichnet, und das Verhältniß v wird sofort:
ν = Q/P = 2pH/δ²E. (50.
Wir wählen nun als besondere dem Meter und Kilogramm als Längen- und
Gewichtseinheit entsprechende Werthe:
E = 900000000, δ = 1/500 = 0,002, p = 800
und erhalten damit die besonderen Beziehungen
Textabbildung Bd. 173, S. 179
mit welchen sich aus unseren oben angenommenen Werthen für Q und H folgende Tabelle
berechnet.
QKilogr.
HMeter.
QHMeterkilogr.
WmKilogr.
a²Quadrtmet.
LMeter.
PKilogr.
v
300
1,8
540
132620
0,0737
4,07
240
5/4
300600
3,61,8
1080
210530
0,1171
5,13
480
5/85/4
600
3,6
2160
334200
0,1857
6,46
960
5/8
Für die weitere Berechnung wollen wir nun aber die Länge der Pfähle etwas vergrößern,
da dieselben nach dem Einrammen immer um etwas abgenommen werden, und mit Belassung
der eben berechneten Gewichte folgende Maaße zu Grunde legen:
a
= 0,m26
,
= 0,m33
,
= 0,m42
,
a²
= 0,□m0676
,
= 0,□m1089
,
= 0,□m1764
,
L
= 4,m40
,
= 5,m50
,
= 6'm80
,
P
= 240 Kgr.
,
= 480 Kgr.
,
= 960 Kgr.
,
ferner wollen wir durchaus
μ = 0,4
setzen und für den Widerstand folgende Scala annehmen.
W
= 540Kgr.
,
= 60000Kgr.
,
= 60000Kgr.
,
= 30000
,
= 90000
,
= 120000
,
= 60000,
,
= 120000,
,
= 180000,
,
= 90000
,
= 150000
,
= 240000
,
= 120000
,
= 160000
,
= 300000
,
= 122740,
,
= 196970= 197270
,,
= 319140
.
Mit diesen Werthen berechnen sich die in der nachfolgenden Tabelle zusammengestellten
Zahlen, aus deren Vergleichung man leicht entnehmen wird, wie wenig die bisher
angenommene Proportionalität der Arbeit des Rammklotzes und der Eintreibung des
Pfahles bei gleichem Widerstande des Erdreiches oder dieses Widerstandes bei
gleichem Eindringen des Pfahles mit den wirklich stattfindenden Verhältnissen
übereinstimmt; man wird sich namentlich durch Vergleichung der in der 2ten und 3ten
horizontalen Abtheilung enthaltenen Ergebnisse, welche sich auf einen und denselben
Pfahl beziehen, überzeugen, daß es für die Eintreibung desselben nicht allein auf
die Arbeit des Rammklotzes ankommt, sondern wesentlich auf das Gewicht des letzteren
und daß der schwerere Rammklotz bei kleinerer Fallhöhe eine
wesentlich größere Wirkung ausübt, als der kleinere Rammklotz bei größerer
Fallhöhe, wenn auch die Arbeiten beider gleich sind.
Construirt man endlich die Ergebnisse der directen Rechnung nach den Gleichungen
(23), (30), (41) und (42), indem man die Werthe von W
als Abscissen und die von z₄ oder z₅ = Z in einem
vergrößerten Maaßstabe als Ordinaten nimmt (wie es in Bezug auf unsere Tabelle in
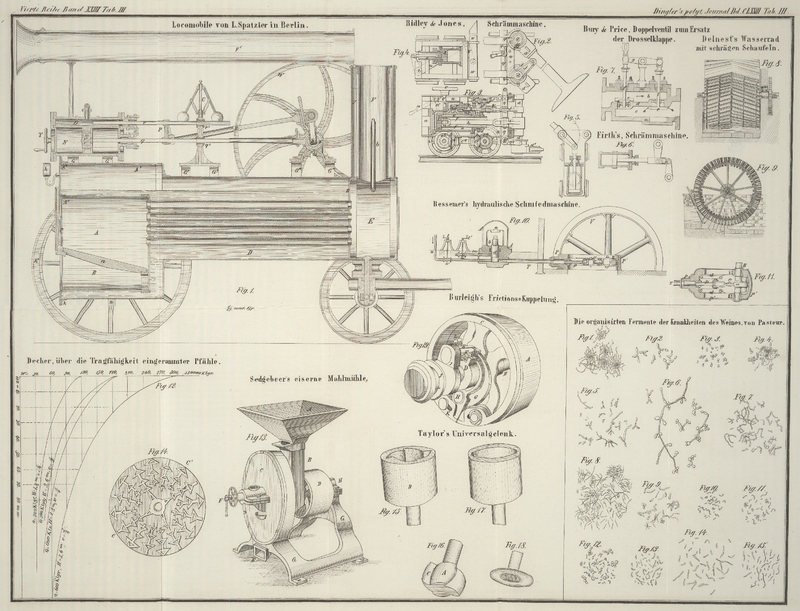
Fig. 12,
worin die verticalen Ordinaten die 10fache Eintreibung des Pfahles für einen Schlag
darstellen, geschehen ist) so hat man nicht nur ein anschauliches Bild von dem
Gesetze, welches zwischen dem Widerstande und der Eintreibung der Pfahlspitze bei
einerlei Arbeit eines Rammklotzes von gegebenem Gewichte stattfindet, sondern auch
ein einfaches und für die Anwendung genaues Mittel zur Lösung der umgekehrten
Aufgabe: Aus der beobachteten Eintreibung die Größe des
Widerstandes zu finden.
In Betreff jenes Gesetzes zeigt unsere Figur eine unverkennbare Aehnlichkeit je der
beiden Curven, für welche das Verhältniß v denselben
Werth hat, und die Durchschnitte der 4 Curven mit der ersten Parallelen zur W-Achse geben für eine Eintreibung = 10mm durch 10 Schläge die Widerstände W = 88500, = 137400 = 150000 und = 228300 Kgr. Will man
dagegen die Größe des Widerstandes für eine Eintreibung = 10mm durch 25 Schläge wissen, so wird man zur
W-Achse eine Parallele in der Entfernung =
4mm ziehen, weil dann 10 Schläge nur
eine Eintreibung von 4mm bewirken können,
und die Abstände der Schnittpunkte dieser Parallelen mit den Curven von der z-Achse werden in dem entsprechenden Maaßstabe
die zugehörigen W angeben.
Textabbildung Bd. 173, S. 181
Gewicht; Fallhöhe; des Rammklotzes;
Länge; Querschnitt; Gewichtsverhältn. zu Q; Compression durch Q; des Pfahles;
Größe; Verhältniß; Winkel; des Widerstandes; Eintreibung der Pfahlspitze im;
Zeitabschnitt; Ganze Eintreibung des Pfahles durch; 1 Schlag; eine Hitze von 25
Schlägen
Tafeln