| Titel: | Ueber die künstlichen Metallconstructionen der Geschützrohre. |
| Autor: | Dy |
| Fundstelle: | Band 177, Jahrgang 1865, Nr. XXXVIII., S. 173 |
| Download: | XML |
XXXVIII.
Ueber die künstlichen Metallconstructionen der
Geschützrohre.
Mitgetheilt von
Artillerie-Hauptmann Dy. in Cassel.
Mit Abbildungen auf Tab.
IV.
Ueber die künstlichen Metallconstructionen der
Geschützrohre.
In dem artilleristischen Nachtrage zu Anderson's
„Anwendung des Copir- oder Uebertragungs-Principes bei der
Anfertigung etc. von Feuerwaffen“ in Bd. CLXIX S. 92 des polytechn.
Journals wurde vom Referenten bereits auf die Wichtigkeit der Erhöhung des
Widerstandsvermögens der Geschützrohre gegen Längenaufreißung durch
Drahtumwickelung, Umreifung (cerclage), oder Kernguß mit
Abkühlung von innen nach außen derselben, aufmerksam gemacht, sowie auf das
Geschichtliche dieser künstlich hervorgerufenen Spannungsverhältnisse des
Rohrmaterials und auch auf den innigen Zusammenhang hingedeutet, den die auf
Rohrverstärkung durch eine solche künstliche Construction des Geschützrohrmetalles
hinzielenden Bestrebungen jetzt mit den durch Steigerung der activen und passiven
Vertheidigungsmittel, wohin z.B. gezogene Geschütze, Panzerung der Schiffe etc.
gehören, hervorgerufenen artilleristischen Forderungen der Zeit:
„treffsichere und kräftige Fernwirkung, überwältigend große
Nahewirkung und möglichst handliche Rohre“ haben. – Die
seitdem, diesen Gegenstand betreffend, im polytechn. Journal gelieferten Referate
über Fortbildung der Frederix'schen
Geschützrohrumreifungs-Methode durch Blakely's
neueste Geschützconstruction (Bd. CLXXV S. 16) und Burr's
Hinterladungs-Geschützrohre (Bd. CLXXVI S. 193), ferner über Verwendung des
Armstrong-Blakely'schen Coil-Principes durch Hitchcock's neuestes System Kanonenrohre zu schmieden
(Bd. CLXXVI S. 15), weiter über Combination der Rohrverstärkung durch umgelegte
Cylinderröhren mit der amerikanischen Methode des Geschützguß-Abkühlens von
innen nach außen von Parrot (Bd. CLXXIII. 331), sowie von
Whitworth und Hulse (Bd.
CLXXI S. 33), und endlich über den Guß eiserner Geschützrohre etc. über einen durch
Luftströmung kühl erhaltenen Kern, sowie über den Rodman'schen Guß des aus der Fort-Pitt-Gießerei zu Pittsburgh
kürzlich hervorgegangenen 1000Pfünders (Bd. CLXXVI S. 279 und 280), – – diese
weiteren Referate über künstliche Metallconstructionen der Kanonenrohre dürften wohl
zur Genüge darauf hinweisen, daß das Gefühl, man nahe sich der Grenze, an welcher,
bei den zur Vermehrung der lebendigen Kraft des Geschosses immer mehr und mehr
gesteigert werdenden Kalibergrößen, homogene Rohre auch selbst des besten Materials,
wenn dessen Theilchen ursprünglich gar keiner Spannung unterliegen, fernerhin nicht
mehr gebrauchsfähig darstellbar seyn möchten, und es wird deßhalb für jetzt an der
Zeit erachtet, diesem Gegenstande hier eine nochmalige wissenschaftliche Besprechung
zu widmen, wozu die in den Nummern vom 3., 17. und 24. December 1864 des Scientific American unter dem Titel:
„Professor Treadwell, über umreifte
Kanonen“ enthaltenen Arbeiten, sowie der neuerdings in Bd. LVII Heft
3 des Archivs für die Officiere der königl. preußischen Artillerie- und
Ingenieur-Corps mitgetheilte: „Beitrag zur Theorie der künstlichen
Metallconstructionen, von dem k. k. österreichischen Ingenieur-Lieutenant
Treuzel“, erwünschte Veranlassungen
darbieten, und wobei auch einige Rohrstärkenberechnung etc. betreffende Stellen der
Werke: „Rutzky, Oberlieutenant der k. k.
Artillerie, die Einrichtung und die Construction der gezogenen
Geschütze“, „Bastien, k. k.
Hauptmann, Lehrbuch der gesammten Artillerie-Wissenschaft“ und
„Dr. Hermann Scheffler, Baurath, die Elasticitätsverhältnisse der Röhren, welche
einem hydrostatischen Druck ausgesetzt sind, insbesondere die Bestimmung der
Wanddicke derselben“, mit in Benutzung gezogen werden mögen.
Als Ausgangspunkt der nun anzustellenden Betrachtung möge die in Professor Treadwell's oben bezeichneten Arbeiten unter der
Ueberschrift: „Größere Pressung in großen als in kleinen
Kalibern“ zu findende Mittheilung der Thatsache dienen, daß bei
ähnlich construirten Rohren und gleichen Geschoß-Anfangsgeschwindigkeiten die
Cohäsionskraft der Rohrwandungen großer Kaliber beim Schusse stärker als diejenige
kleinerer Kaliber in Anspruch genommen wird. Der genannte Autor stellt hierüber eine
Berechnung auf, wornach die Wände eines zehnzölligen Rohres für jeden Quadratzoll
ihrer Bohrungsfläche das 3,35 fache von dem Gasdrucke aushalten müssen, welcher
gegen die Seelenwand eines zweizölligen Geschützrohres ausgeübt wird, wenn beide
Rohre kaliberdurchmessergleiche Wandstärken haben und ihren respectiven gußeisernen
Rundkugeln beim Schusse gleiche Anfangsgeschwindigkeiten ertheilt werden sollen, und
weiter wird in den bezeichneten Mittheilungen Prof. Treadwell's zum Beweise dafür, daß bei solchen Rohren, welche einen
bedeutenden inneren Gasdruck aushalten müssen, dann zum Widerstande gegen diese Gasspannungen
verhältnißmäßig sehr große Wandstärken eintreten müßten, noch Kenntniß davon
gegeben, daß bei einem homogenen Rohre von anfänglich ganz gleicher Spannung aller
seiner Wandtheilchen, dessen äußerer Radius fünfmal so groß als sein innerer ist,
sich in 41 gleich weit von einander entfernten Ringschichtenflächen des Rohres die
Widerstände des homogenen Wandmaterials gegen eine Längenaufreißung des Rohres, wenn
von innen nach außen hin gerechnet wird, verhalten würden wie die Zahlen:
1000
250
111
62
826
225
104
59
694
207
98
56
591
189
92
54
510
174
87
51
444
160
82
49
391
148
77
47
346
137
73
45
309
128
69
43
277
119
110
65
41
40
Die erstere Rechnung zum Klarmachen des Umstandes, daß die Cohäsionskraft der
Wandungen ähnlich construirter Geschützrohre bei großen Kalibern unter sonst
gleichen Schußverhältnissen mehr in Anspruch genommen wird als dieses bei kleineren
Kalibern der Fall ist, wird für das angegebene Zahlenbeispiel etwa folgend geführt:
Angenommen, das zwei- und das zehnzöllige Geschützrohr mit ihren gußeisernen
Rundkugeln von beziehungsweise 1 und 125 Pfund Gewicht hätten Patronen von gleicher
Länge, so würde auf jeden Quadratzoll der Größtkreise beider Geschosse dasselbe
Pulverquantum kommen und das Gewichtsverhältniß beider Ladungen dann 1 : 25, das der
Geschosse aber 1 : 125 seyn. – Der Pulverladung des zehnzölligen Rohres steht
dann verhältnißmäßig also ein fünfmal so großes Kugelgewicht entgegen als der Ladung
des zweizölligen Rohres, was für letzteres einem Geladenwerden desselben mit fünf
aufeinander gesetzten Kugeln seines Kalibers entsprechen würde. Setzt man die durch
Geschosse verschiedener Schwere bei constanter Ladung bedingt werdenden
Gasspannungen, welche beim Schusse im Innern des Rohres entstehen, den dritten
Wurzeln der respectiven Geschoßgewichte proportional, so würde diese Ladung mit fünf
Kugeln also schon einer ∛5 = 1,71fachen Inanspruchnahme der
Zusammenhangskraft des Rohrmaterials gleichkommen. – Mit einer solchen Ladung
des zehnzölligen Rohres, welche bei 1/3 kugelschwerer Ladung des zweizölligen Rohres
für ersteres nur etwa 8 1/3 Pfd. oder circa 1/15
Kugelgewicht betragen würde, läßt sich aber dem 125pfündigen Geschosse des zehnzölligen
Geschützes eine nur sehr geringe, für den gewöhnlichen Gebrauch ganz unzureichende
Anfangsgeschwindigkeit ertheilen und soll dieselbe statt dessen genau so groß wie
die Anfangsgeschwindigkeit der mit 1/3pfündiger Pulverladung abgeschossenen
einpfündigen Kugel, also etwa gleich 1600 Fuß pro
Zeitsecunde seyn, so dürfte man, da eine fünffache Patronenlänge 41 2/3 Pfd.
Pulverladung ergeben würde, mit Rücksicht auf den relativ kleineren Spielraum des
größeren Kalibers und die Möglichkeit einer Verdoppelung der Rohrlänge des
zehnzölligen Geschützes, dem letzteren etwa 30 bis 35 Pfd. Ladung zu geben haben.
– Die selbst bei der Annahme von nur 30 Pfd. durch diesen Ladungszuwachs
vermehrt werdende Pressung der Pulvergase gegen die inneren Rohrwandungen beim
Schusse ist, wenn die Gasspannungen im Rohre den durch sie bedingten
Anfangsgeschwindigkeiten des in seinem Gewichte constant bleibenden Geschosses und
also auch den Quadratwurzeln aus den Ladungsgewichtszahlen annähernd proportional
gesetzt werden, im vorliegenden Falle durch das Gasdruckverhältniß von 1 : 1,96
ausgedrückt, welches letztere, mit dem früheren Pressungsverhältnisse von 1 : 1,71
zusammengesetzt, das oben behauptete Druckverhältniß von 1 : 3,35 ergibt, nach
welchem die Bohrungswand des 150Pfünders beim Schusse stärker pro Quadratzoll als diejenige des 1Pfünders gepreßt wird, wenn beide
Geschütze ihren Geschossen gleiche Anfangsgeschwindigkeit ertheilen sollen.
Diese Ausführung weist an sich zwar noch keineswegs auf die Nothwendigkeit der
Umpanzerung oder einer sonstigen künstlichen Metallconstruction der für starke
Ladungen bestimmten Rohre größerer Kaliber, sondern zunächst nur auf den Ausweg hin,
welchem die sogenannten Dahlgren-Rohre ihre
Entstehung verdanken, daß man nämlich dahin strebt, die Metallstärke in jedem Punkte
des Längendurchschnittes der Rohre immer genau derjenigen zerreißenden Kraft
anzupassen, welche bei dem Schusse auch wirklich auf den betreffenden Punkt dieses
Schnittes einwirkt und so durch sachentsprechende Experimente endlich zu einem
Geschützrohre gelangt, dessen Metallstärke gegen jene der alten Rohre zwischen
Mündung und Schildzapfen bedeutend verringert, am Bodenstücke aber, wo die größte
Festigkeit nöthig ist, mit dem dort gesparten Material in einer den wirklichen
Schußverhältnissen entsprechenden Weise vermehrt erscheint. In den Vereinigten
Staaten Nord-Amerika's verfährt man nach der von Capitän Dahlgren angegebenen Constructionsmethode hierbei auf
folgende Weise: Etwas über ein Kaliber hinter der Mündung des zu dem Experimente zu
verwendenden Rohres wird eine Queröffnung von der äußeren Oberfläche bis zur Bohrung
durchgebohrt und in
diese Oeffnung ein Projectil von bestimmtem Gewichte genau eingepaßt. Das Rohr wird
dann geladen und abgefeuert. Sobald das Geschoß an der Oeffnung vorüber ist und die
Pulvergase letztere erreichen, wird das in derselben befindliche Projectil gegen ein
ballistisches Pendel geschleudert, und die Geschwindigkeit, mit welcher dieses
geschieht, genau gemessen. – Hierauf werden nach der Reihe und in gleichen
Abständen mehrere solche Queröffnungen nacheinander bis zum Ladungsraum
fortschreitend gebohrt, jede mit einem Projectile von gleichem Gewichte wie das
erste verschlossen und die Geschwindigkeit, mit welcher das Projectil in das Pendel
geschleudert wird, ebenso bestimmt. Die Geschwindigkeit dieser Projectile ist dann
ein Maaß der relativen Explosionskraft in den entsprechenden Abständen der
Oeffnungen vom Seelenboden und folglich auch der relativen Metallstärke, welche an
jeder dieser Oeffnungen nöthig ist, – vorausgesetzt daß einer
n
fachen Wandstärke auch immer eine n
fache Widerstandskraft gegen Längenaufreißung des Rohres
parallel zu seiner Achse zukommen müsse, daß also alle
Rohrpartikelchen gleichmäßig an dem Widerstande gegen eine solche
Rohrzerreißung Theil nehmen, was bei Rohren, deren Theilchen ursprünglich gar keiner Anstrengung
unterliegen, sondern sich gegenseitig im
vollkommenen Gleichgewichte befinden, aber offenbar nicht der Fall seyn kann, da es Thatsache ist, daß man
die Widerstandskraft der vor ihrer Pressung im natürlichen Zustande befindlichen
Röhren von hydraulischen Pressen durch Vermehrung ihrer Wanddicken über ein gewisses
Maaß hinaus nicht zu steigern vermag, ein Umstand welcher Longridge bekanntlich zur Verstärkung solcher Röhren durch
Drahtumwickelungen veranlaßte, welche Verstärkungsmethode von Oberst Treuille de Beaulieu dann auch auf Geschützrohre
angewendet wurde, in dieser letzteren Verwendung, obgleich an sich sehr rationell,
aber durch den Uebelstand beeinträchtigt erscheint, daß die Drahtumwickelung sich
gänzlich auflöst, sobald der Draht an irgend einer Stelle zerrissen wird, was bei im
Gefechte befindlichen Geschützrohren durch das Anschlagen feindlicher Projectile
etc. natürlich leicht vorkommen kann.
Diese als Thatsache feststehende Abnahme der Möglichkeit, die
Stärke der Röhren hydraulischer Pressen durch
Vermehrung der Dicke ihrer aus homogenem Material bestehenden Wandungen beliebig
steigern zu können, ist aber aus dem Umstande zu erklären, daß bei einem
derartigen Rohre, welches in seiner Bohrung einen genügend großen Druck erfährt, die
Spannung der äußeren Umfangsschichten jener an der inneren
Wand nicht gleich,
sondern kleiner als diese ist, und hierauf beziehen sich
denn auch die oben mitgetheilten 41 Verhältnißzahlen, welche, als von Professor Treadwell herrührend, den Maaßstab für die in eben so
vielen Ringschichtenflächen gleichen Abstandes von einander von innen nach außen hin
abnehmenden Spannungen des homogenen Rohrwand-Materials einer in ihrem
Inneren mit genügend starker Pressung versehenen Cylinderröhre abgeben sollen, deren
Wandstärke gleich dem 2 1/2 fachen des Durchmessers ihrer inneren Ausbohrung ist.
– Leider ist für diese Verhältnißzahlen an der oben bezeichneten Stelle aber
nicht auch zugleich der Weg angegeben, auf welchem dieselben gefunden worden sind,
während gerade die wissenschaftliche Feststellung des
Gleichgewichts-Zustandes eines homogenen Cylinders unter der Einwirkung von
Kräften, die sich normal gegen dessen gekrümmte Oberflächen äußern, offenbar als das
Fundament der Anordnung und Beurtheilung aller künstlichen Metallconstructionen in
Rede stehender Art zu bezeichnen ist, und es soll daher versucht werden, der sonach
zum Verständniß der vorliegenden Frage durchaus nothwendigen Entwickelung jenes
Gleichgewichts-Zustandes hier in der Weise zu genügen, daß man die ältesten
der in dieses Gebiet einschlagenden Formeln allmählich zu den neuesten und besten,
dem Referenten bekannten Ausdrücken derselben Art überführt.
Bezeichnet man zu dem Ende vorerst
mit r den Radius irgend einer
Umfangsschichtfläche des gegebenen concentrischen Cylinders, sowie mit r₀ und r₁
beziehungsweise den inneren und den äußeren Radius desselben;
mit N₀ u. N₁ beziehungsweise den von innen und den von
außen gegen das cylindrisch gebohrte Rohr angewendeten Normal-Druck pro Quadrateinheit;
mit T die am Ende des Radius r herrschende Tangential-Spannung der
betreffenden ringförmigen Fiber des Rohrmaterials, mit T₀ und T₁ also beziehungsweise die
Spannungen der Rohrwandung an ihrem inneren und an ihrem äußeren Umfange und
mit δ die Wanddicke r₁ –
r₀r₀ – r₁ des Rohres, so ist zunächst für eine Rohr-Ringschicht von der Länge
= 1 die Summe aller Komponenten für die inneren Pressungen gleich 2r₀N₀, nämlich
gleich dem normalen Drucke gegen einen centralen Längendurchschnitt des inneren
Röhrenraumes von der Länge = 1, denn bezeichnet AB =
2r₀ den inneren und EF = 2r₁ den äußeren
Vertical-Durchmesser eines cylindrisch gebohrten Rohres von der Länge gleich
einer Längeneinheit
und α den Winkel, welchen die Richtung des an
irgend einem Punkte des inneren Umfanges gedachten Normal-Druckes N₀ mit diesen verticalen Durchmessern bildet, so
kann man diesen Druck in zwei aufeinander senkrecht wirkende Seitenkräfte N₀' und N₀''
zerlegen, von denen der eine parallel zu AB, der andere
also senkrecht darauf ist, und erhält dann N₀' =
N₀ cos α
und N₀'' = N₀
sin α. – Der Druck auf einen am
Endpunkte des inneren Radius r₀ liegenden
unendlich schmalen Flächenstreifen der inneren Bohrungswand, dessen Länge gleich 1
und dessen Bogen gleich r₀ dα ist, wird also senkrecht gegen AB
gleich r₀ dαN₀ cos α und parallel zu
AB gleich r₀ dα N₀ sin α, der senkrecht auf AB wirkende Gesammtdruck gegen die halbe innere Cylinderfläche also
Textabbildung Bd. 177, S. 179
seyn, welchem der ebenwohl senkrecht zu AB auf die zweite halbe innere Cylinderfläche wirkende Gegendruck gleich
ist, während die parallel zu AB wirksamen Pressungen auf
eine Trennung des Rohres nach der Richtung AB hin gar
keinen Einfluß haben können. Es ist also der Gesammtdruck, welcher durch die
Normalkraft N₀ auf beide innere Flächenhälften
eines eine Längeneinheit langen Rohres vom Bohrungsradius r₀ zur Zerreißung desselben in der Richtung irgend eines seiner
Durchmesser AB ausgeübt wird, immer gleich 2r₀N₀.
Ebenso wird die Summe aller Componenten für die von außen auf das Rohr einwirkenden
Normalpressungen gleich 2 r₁ N₁ und folglich die auf das Rohr von innen nach
außen hin normal einwirkende Gesamimkraft = 2r₀N₀ – 2r₁N₁ seyn.
Nimmt man nun an, die dem Zerreißen des Rohres nach irgend einem seiner Durchmesser
hin und parallel zur Rohrachse sich entgegenstemmenden Tangentialkräfte seiner ringförmigen Wandungssibern seyen in allen Punkten der Rohrwand einander gleich, also
überall gerade so groß, wie z.B. die Tangentialspannung T₀ des Rohrmaterials an der inneren Bohrungsfläche, so hat man, da
die Zerreißungsfläche eines Rohres von der Länge Eins nach der Richtung irgend eines
seiner Durchmesser hin für den inneren Radius = r₀ und den äußeren Radius = r₁ als
Summe zweier gleichen Rechtecke von der Größe (r₁ – r₀) l = r₁ – r₀
gefunden wird, für die Summe aller einer solchen Rohrzerreißung sich widersetzenden
tangentialen Spannkräfte des Rohrmaterials die Größe 2 (r₁ – r₀) T₀ und folglich, wenn Gleichgewicht der in Rede
stehenden Kräfte stattfinden soll, die Relation:
(r₁ – r₀) T₀ = r₀ N₀ –
r₁ N₁
woraus für die Tangential-Spannung T in jedem Punkte der Rohrwand am Endpunkte des Radius
r:
Textabbildung Bd. 177, S. 180
und für die Wanddicke:
Textabbildung Bd. 177, S. 180
folgt, was für die Praxis, wenn ferner noch
mit f die absolute Festigkeit des
Rohrmateriales nach tangentialer Richtung hin, und
mit n der
Sicherheits-Coefficient bezeichnet werden, die innere Rohrspannung T₀ also gleich 1/n f
gesetzt wird, eine zur Sicherheit gegen Zerreißung im angegebenen Sinne nothwendige
Rohrwanddicke:
Textabbildung Bd. 177, S. 180
ergibt.
Dieses ist die älteste Formel für die Wanddicke hohler
Cylinder, welche man auch jetzt noch in den meisten Lehrbüchern, und, mit
Vernachlässigung des äußeren Atmosphärendruckes N₁, also für N₁ = 0, auch in den
oben angeführten Werken von Rutzky und Bastien noch beispielsweise zur annähernden Berechnung
der Bodenstück-Wandstärken von solchen Kanonenrohren angewendet findet,
welche am Patronenlager einen inneren Pulvergasdruck von in runder Zahl 1300
Atmosphären oder 16575 Wiener Pfd. pro Wiener
Quadratzoll des Rohrquerschnittes und beziehungsweise der Seelenwand auszuhalten
haben, wie dieses nach den von Major Neumann und Oberst
Majewsky früher angestellten Versuchen z.B. beim
glatten 6 Pfünder mit 1/3 kugelschwerer Ladung wirklich der Fall ist. – Setzt
man zu einer dergleichen Rechnung nämlich den Festigteits-Coefficienten f, d.h. die zerreißende Kraft für 1 Quadratzoll des
Querschnittes vom Rohrmaterial
bei Gußeisen aus dem Hohofen
= 24000 bis 24300 Pfund
bei Gußeisen in Flammöfen umgeschmolzen
= 28000 bis 36000
„
bei Geschützbronze
= 34009 bis 38000
„
bei Gußstahl
= 71000 bis 120000 „
so erhält man nach oben angegebener Formel, die Rohrspannung
T₀ gleich der absoluten Festigkeit f des Rohrmateriales gesetzt, für einen 6 Pfünder vom
Bohrungsradius r = 1,8 Zoll rheinländisch, als
Wandstärken δ am Patronenlager, bei welchen
annähernd ein Gleichgewichtszustand der sich entgegenstehenden Kräfte des Rohres und
des Pulvers stattfinden, das Rohr also eben der Länge nach aufreißen würde:
für Gußeisen
δ = 0,70r
bis 0,46r
für Geschützbronze
δ = 0,48r
bis 0,43r
für Gußstahl
δ = 0,23r
bis 0,14r
und, wenn der Sicherheits-Coefficient n hier gleich 3 angenommen, T₀ also gleich 1/3 f gesetzt wird, so
erhielte man hiernach als genügende Sicherheit gegen Rohrzerreißung darbietende
Bodenstück-Wandstärke:
für Gußeisen
δ = 2,10r
bis 1,38r
für Geschützbronze
δ = 1,34r
bis 1,29r
für Gußstahl
δ = 0,69r
bis 0,42r.
Da bei Ableitung dieser zur Bestimmung der Rohr-Metallstärken dienen sollenden
Formel aber die Ausdehnbarkeit und Elasticität der Rohrmaterie gar nicht in Rechnung gezogen worden ist, diesen Eigenschaften zufolge aber bei einem Rohre welches
in seiner Bohrung einen genügend starken Druck erleidet, die Spannung an der äußeren Umfangsschicht nicht, wie oben stillschweigend
vorausgesetzt wurde, jener an der inneren Wand gleich, sondern
kleiner als diese ist, wie jetzt nachgewiesen werden soll, so kann diese
Formel offenbar nur für röhrenförmige Körper von sehr geringer
Wanddicke Anwendung finden, weil nur in diesem Falle die Voraussetzung
einer gleichmäßigen Vertheilung der
Tangential-Spannung des Rohrmaterials über die ganze
Dicke der Rohrwand zulässig ist. Für Kanonenrohre etc. muß aber, wenn
Genauigkeit der Rechnung stattfinden soll, offenbar die jedesmalige
Tangentialspannung T der elastischen Rohrmaterie vom
zugehörigen Radius r der betreffenden Schalenschicht in
sachentsprechender Weise abhängig gemacht werden. Ist hiernach dann T als Function von r
bekannt, so muß die Spannung irgend einer concentrischen
Schale vom ursprünglichen Radius r und der
unendlich geringen Wanddicke dr an einer der beiden
diametral gegenüberliegenden Zerreißungsflächen von der Länge = 1 offenbar gleich
Tdr, die Summe der
Tangentialkräfte aller die Rohrwand bildenden Schalenschichten an beiden
Bruchflächen des nach der Richtung seines Durchmessers zu zerreißenden Rohres von der Länge
„Eins“ also gleich
Textabbildung Bd. 177, S. 182
und, da zwischen dieser Spannung und der ausdehnenden Kraft 2
(r₀N₀
– r₁N₁)
Gleichgewicht stattfinden soll
Textabbildung Bd. 177, S. 182
seyn.
Es kommt für eine rationelle Lösung des vorliegenden
Problems also jetzt zunächst darauf an, die Tangentialspannung T des Rohres in
irgend einer seiner concenirischen Schalenschichtflächen der Wandung möglichst sachentsprechend als Function des zugehörigen Radius
r auszudrücken. Bedient man sich zu diesem
Ende nach Brix.
2) der Hypothese, die Dicke der Rohrwand und diejenige jeder
elementaren Schalenschicht derselben erleide bei der Ausdehnung des Rohres
durch innere Pressungen gar keine Veränderung, es
entspreche bei dieser Dehnung der ringförmigen Material-Elementartheile deren
Volumvermehrung also immer ganz genau ihrer Längenzunahme, so ist dann die
Vergrößerung ρ des Radius r offenbar eine constante Größe und es verhält sich also, wenn man die
Spannung einer Rohrschalenschicht vom Radius r mit T und weiter
mit E den Elasticitätsmodul des
Rohrmaterials, d.h. diejenige Zugkraft bezeichnet, welche einen cylindrischen oder
prismatischen Körper desselben von der Länge = 1 und dem Querschnitte = 1,
vorausgesetzt daß dabei die Elasticitätsgrenze nicht überschritten wird, um seine
eigene Länge = 1 auszudehnen vermöchte:
E : T = 1
: ρ /r
weil die Spannungen eines
elastischen Körpers innerhalb seiner Elasticitätsgrenze den ausdehnenden Gewichten und diese wieder den durch sie hervorgebrachten Längenvermehrungen proportional sind, für eine Dehnung
des Rohrschichten-Radius r um die Größe ρ der betreffende Schalenumfang aber von 2rπ in 2 (r +
ρ) π = 2rπ (1 + ρ/r)2 (r + ρ)
T = 2 (1 + r/
ρ) T übergeht, also um den ρ /r Theil seiner Länge zunimmt.
Hiernach ist also
T = (ρ/r) E
wornach sich, diesen Werth in obige Grundgleichung
Textabbildung Bd. 177, S. 183
substituirt:
Textabbildung Bd. 177, S. 183
und, wenn man für ρ = ρ₁ = ρ₀ den Werth r₀T₀/E einsetzt:
Textabbildung Bd. 177, S. 183
ergibt, aus welcher letzteren Gleichung dann durch
Integration
r₀ T₀ log nat r₁/r₀ = r₀ N₀ – r₁
N₁,
und somit die Spannung T₀
des Rohrmaterials an der inneren Bohrungswand desselben
Textabbildung Bd. 177, S. 183
folgt, welche Formel, wenn man sehr
dünne Rohrwände voraussetzt, so daß annähernd
r₁/r₀ – 1 = log nat r₁/r₀
also
Textabbildung Bd. 177, S. 183
angenommen werden kann, in die zuerst von Brix aufgestellte Formel
Textabbildung Bd. 177, S. 183
übergeht, aus welcher die Dicke δ der Rohrwand:
Textabbildung Bd. 177, S. 184
und für den praktischen Gebrauch, wenn der
Sicherheits-Coefficient mit n und die absolute
Materialfestigkeit mit f bezeichnet werden, für T₀ also der Werth
T₀ = 1/n f
in die Rechnung einzuführen ist,
Textabbildung Bd. 177, S. 184
folgt, eine Formel, welche mit Streichung des äußeren
Normaldruckes N₁ auf die Rohrwand im Nenner ihres
Exponenten, also in der Form von
Textabbildung Bd. 177, S. 184
den gesetzlichen Bestimmungen über die Wanddicke der Dampfkessel in verschiedenen Staaten zu Grunde liegt.
Bedient man sich, um die Tangentialspannung T des
Rohrmaterials an irgend einer Stelle vom Radius r
desselben als Function des zugehörigen Radius r
darzustellen, aber nach Barlow
3) der Hypothese, daß bei Ausdehnung des Rohres der Querschnitt
der Rohrwand stets denselben Flächeninhalt beibehalte, das Volum der Rohrwand hierbei also ungeändert bleibe, so daß, wenn r in r + ρ übergeht, also
immer
[(r + ρ)² – (r₀ + ρ₀)²] π = (r² – r₀²) π(r₁ – r₀)² π
d.h., wenn man die zweiten Potenzen von ρ und von ρ₀, als sehr
kleiner Theile von r und r₀ gegen beziehungsweise 2r und 2r₁ vernachlässigt:
ρ = r₀ρ₀/r
seyn müßte, so erhält man, diesen Werth von ρ in obenstehende Grundgleichung
Textabbildung Bd. 177, S. 184
substituirt:
Textabbildung Bd. 177, S. 185
und nach der Proportion
E : T₀ = 1 : ρ₀/r₀
für E seinen Werth E = (r₀T₀/ρ₀)
gesetzt:
Textabbildung Bd. 177, S. 185
woraus durch Integration:
Textabbildung Bd. 177, S. 185
folgt. –
Es ist nach dieser Hypothese also die Tangentialspannung T des Rohrmaterials an der inneren Bohrungswand:
Textabbildung Bd. 177, S. 185
und, wenn man den äußeren Normaldruck N₁ vernachlässigt, also N₁ = 0
setzt,
Textabbildung Bd. 177, S. 185
woraus die Wanddicke
Textabbildung Bd. 177, S. 185
und für den praktischen Gebrauch, wobei wieder T₀ = 1/n
f zu setzen ist
Textabbildung Bd. 177, S. 185
folgt. –
Diese, zuerst von Barlow aufgestellte Formel wurde 1859
von Capitän Blakely in England zu seinen Untersuchungen
über die Wandstärke von Kanonenrohren etc. angewendet, und neuerdings ist dieselbe
in den oben erwähnten artilleristischen Lehrbüchern von Rutzky und Bastien für derartige Untersuchungen
wieder, jedoch mit der Modification:
δ = r₀N₀/(r₀T₀ – N₀)
in Vorschlag gebracht worden, welche Anordnung dort etwa
folgende Motivirung findet:
Innerhalb der Elasticitätsgrenze verhält sich nach den angenommenen Bezeichnungen
T : T₀ = ρ/r
: ρ₀/r₀
woraus die tangentiale Spannung T
am Ende des Radius r
T = T₀ ρr₀/rρ₀
und, für ρ seinen, der Barlow'schen Hypothese entsprechenden Werth ρ = r₀ρ₀/r
gesetzt
T = T₀ r₀²/r²
folgt. – Der Widerstand, welchen eine elementare
Schalenschicht von der Dicke dr gegen Zerreißung bietet,
ist dann:
Tdr = T₀ r₀²/r² dr
und daraus wird für den Gesammtwiderstand W der Rohrwand gegen Längenaufreißung durch Integration
zwischen den Grenzen r₁, und r₀ gefolgert:
Textabbildung Bd. 177, S. 186
welche Gleichung, wenn der Gesammtwiderstand W des Rohres dem Normaldrucke N₀ auf seine innere Wandfläche gleich gesetzt wird, die
Metallstärke δ, bei welcher das Rohr durch diesen
inneren Druck eben zerreißen müßte:
δ = r₀N₀/(r₀T₀ – N₀)
ergeben würde.
Sucht man endlich, nach Lamé,
4) die wirkliche Formveränderung irgend einer
concentrischen Rohrwand-Schalenschicht vom Radius r und der Dicke dr, wie sie der dort
herrschenden Tangentialspannung T und der dieselbe
verursachenden Normalpressung N entspricht, nach
allgemeinen mechanischen Grundsätzen zu bestimmen, indem die Verkürzung eines in radialer Richtung liegenden Fibernelementes des Rohrmateriales,
welche demselben bei Verlängerung des Radius r um die
Größe ρ
Zusammenpressung durch den hier wirkenden Normaldruck N pro Quadrateinheit zukommen muß, für den
Elasticitätsmodul E, als dr
N/E in Rechnung gezogen, also
ρ + dρ = ρ – dr N/E
gesetzt wird, woraus
dρ/dr = – N/E
folgt, so ist, weil bei Verlängerung des Radius r um ρ, der
entsprechende Elementarschalenschicht-Umfang nach Obigem um ρ/r seiner Länge zunimmt, nach der
Proportion:
E : T = 1
: ρ/r
ρ = r
T/E
mithin, nach r differenzirt,
auch
dρ/dr = (rdT + Tdr)/Edr,
folglich, beide Ausdrücke für dρ/dr einander gleich gesetzt,
(rdT + Tdr)/Edr = – N/E,
woraus
N = – (r dT/dr + T)
und nochmals nach r
differenzirt
dN/dr =
– (r
d²T/dr²r d²T/dr + 2 dT/dr)
folgt.
Für eine Schalenschicht von der unendlich kleinen Dicke dr kann aber die Tangentialspannung T des
Rohrmaterials als überall gleich groß angenommen werden.
– Es ist also, wenn in der ersten auf eine solche constante Tangentialkraft basirten Grundformel:
(r₁ – r₀) T₀ = r₀ N₀ –
r₁ N₁
r₀ = r,
r₁ = r + dr, T₀ = T, N₀ = N und N₁ = N + dN
gesetzt wird, im vorliegenden Falle:
Tdr = rN – (r + dr) (N + dN)
= – rdN – Ndr
woraus
T = – r (dN/dr) –
N
und, wenn man in diese Gleichung für N und für dN/dr
ihre soeben festgestellten Werthe einsetzt:
r (d²T/dr) + 3
dT/dr = 0
folgt.
Bezeichnet man zur Ausdrucksvereinfachung den Werth dT/dr mit x, so
ist also
r (dx/dr) = – 3x,
woraus
dx/x =
– 3 (dr/r)
und durch Integration zwischen den beziehungsweisen Grenzen
x₀ und x sowie
r₀ und r
log nat x/x₀ = 3 log nat r₀/r = log nat
r₀³/r³
folgt. – Es ist also
x = dT/dr = x₀r₀³/r³
oder
dT = (x₀r₀³/r³)dr,
woraus durch Integration zwischen den beziehungsweisen Grenzen
T₀ und T sowie
r₀ und r
Textabbildung Bd. 177, S. 188
folgt, in welche Gleichung noch für x₀, da oben ganz
allgemein
N = – (r dT/dr + T) = – (rx + T)
gefunden wurde, der Werth
x₀ = – (T₀ + N₀)/r₀
einzusetzen steht.
Man erhält dann die Tangentialspannung:
Textabbildung Bd. 177, S. 189
und, diesen Werth in die sub 1
entwickelte Grundformel:
Textabbildung Bd. 177, S. 189
welche ganz allgemein die Abhängigkeit der Tangentialkraft T vom zugehörigen Radius r
ausdrückt, substituirt:
Textabbildung Bd. 177, S. 189
woraus durch Integration
Textabbildung Bd. 177, S. 189
und folglich die Tangentialspannung T₀ des Rohrmaterials an seiner inneren Wandfläche
Textabbildung Bd. 177, S. 189
sowie die Normalkraft N₀
daselbst
Textabbildung Bd. 177, S. 189
und endlich die Wanddicke δ
= r₁ – r₀ des Rohres
Textabbildung Bd. 177, S. 189
für den praktischen Gebrauch bei n
facher Sicherheit und einer absoluten Festigkeit f des
Rohrmaterials also
Textabbildung Bd. 177, S. 189
und mit Vernachlässigung des äußeren Normaldrucks N₀ auf die Rohrwand
Textabbildung Bd. 177, S. 189
folgt. –
Die Grenze für alle Möglichkeit, ein aus homogenem Material bestehendes Rohr durch Vergrößerung seiner Wandstärke gegen Längenaufreißung durch einen inneren Normaldruck
N₀ schützen zu können,
liegt also für jedes Material immer da, wo die innere normale Pressung
N₀ gleich der
Festigkeit
f
des Materials oder noch genauer
N₀ = f + 2 N₁
ist. Wird diese Grenze des inneren
Druckes überschritten, so erhält man für die Wandstärke
δ einen imaginären
Werth, d.h. es gibt in diesem Falle keine auch noch
so große Wandstärke, welche bei natürlicher Metallconstruction derselben,
den gestellten Festigkeitsbedingungen genügen könnte.
Diese Formeln sind zuerst von Lamé aufgestellt
worden, werden in englischen Schriften aber auch Dr. Hart zugeschrieben und befreit man, um mittelst derselben
schließlich auf einen Ausdruck für den Gesammtwiderstand
eines Rohres gegen Längenaufreißung zu kommen, die allgemeine Tensionsformel:
Textabbildung Bd. 177, S. 190
von N₀, also von dem
Größenausdruck des auf die innere Rohrwand wirkenden Normaldrucks, indem man in
diese Formel nach Obigem für N₀ seinen Werth
Textabbildung Bd. 177, S. 190
einsetzt, so erhält man für die in irgend einer Schalenschicht-Fläche vom Radius r vorhandene Tangential-Widerstandskraft T der Rohrwand gegen Längenaufreißung des Rohres
parallel zu seiner Achse:
Textabbildung Bd. 177, S. 190
folglich den Widerstand gegen derartige Rohrzerreißung in
einer elementaren Schalenschicht von der Dicke dr, welcher sich auf einer Zerreißungsfläche von der
Länge = 1 äußern wird:
Textabbildung Bd. 177, S. 190
und durch Integration zwischen den Grenzen r₁ und r₀ den
Gesammtwiderstand des Rohres auf einer seiner beiden
Zerreißungsflächen:
Textabbildung Bd. 177, S. 190
woraus, das Radienverhältniß r₁/r₀ der Kürze wegen gleich q gesetzt, für den Gesammtwiderstand
W
des Rohres auf beiden diametral sich entgegenstehenden
Längenaufreißungsflächen
Textabbildung Bd. 177, S. 191
folgt.
Für ein constantes T, also für gleiche Tangentialspannung
in allen Elementarschichten des Rohres, würde die Widerstandskraft W₁ desselben gegen Längenaufreißung aber
W₁ = 2 (r₁ – r₀) T₀ = 2 (qr₀
– r₀) T₀ = 2 r₀T₀ (q – 1)
betragen haben und es besteht also zwischen dem ideellen Widerstandsvermögen
W₁, welches ein homogenes Kanonenrohr bei gleicher
Tangentialspannung aller seiner ringförmigen Fibern gegen Längenaufreißung
haben würde und dem reellen Widerstand
W, den es vermöge der Ausdehnbarkeit und Elasticität seines Materials
einer solchen Zerreißung wirklich entgegenzustellen hat,
das Verhältniß:
W₁ : W = 2 r₀T₀ (q – 1) : 2 r₀T₀ (q² – 1)/(q² + 1)
= q² + 1 : q + 1
wornach als relative
Widerstandsleistung des Rohres gegen Längenaufreißung parallel zu seiner
Achse der Quotient
W/W₁ = (q + 1)/(q² + 1)
auftritt.
Dieser Bruch muß, da r₁/r = q naturgemäß immer größer als 1 ist, stets
ein echter seyn, und es gibt derselbe in seinem Verhältnisse zur Einheit stets denjenigen Theil des ideellen
Widerstandsvermögens eines homogenen Rohres an, welcher demselben ganz unabhängig von der sonstigen specifischen
Beschaffenheit seines ausdehnbaren und elastischen Wandmaterials zukommen würde, wenn alle seine Theilchen gleichmäßig vom inneren Normaldrucke
ausgedehnt würden, demselben also auch einen gleichmäßigen Tensionswiderstand entgegensetzten.
Für Werthe von r₁/r₀ beziehungsweise 1,1, 3, 5 verwenden Rohre homogenen Materiales
irgend einer Art, wenn dasselbe nur ausdehnbar und elastisch ist, also nur
beziehungsweise 0,95, 0,4, 0,23 ihres ideellen Widerstandsvermögens zum Widerstande
gegen Längenaufreißung nach ihrer Achsenrichtung hin, und es werden also Rohre des
dritten Falles, deren Wandstärken nach der sub 1
aufgeführten alten Formel
δ = r₀N₀/(1/n)f
construirt sind, selbst wenn der Sicherheitscoefficient dabei
anstatt 3 gleich 1/0,23 = 4,35 angenommen worden wäre, mit Nothwendigkeit zerreißen
müssen.
Die relative Widerstandsleistung homogener Kanonenrohre irgend
eines Materials, wenn dasselbe nur ausdehnbar
und elastisch ist, nimmt also mit
dem Wachsen des Radienverhältnisses
r₁/r₀ sehr rasch ab und wird von diesem Verhältnisse endlich
die Reciproke 1/n
des Sicherheitscoefficienten n
überschritten, so muß ein in seinen Wandstärken nach der alten Formel
construirtes Rohr dieser Art zerreißen, wenn dessen
Tension an der inneren Rohrwand dabei der absoluten Materialfestigkeit gleichgesetzt
worden war, und es wird dann nur noch von der größeren oder geringeren Dehnbarkeit und Schmiegsamkeit
des Rohrmaterials abhängen, ob dasselbe wie bei Rohren von Bronze, Schmiedeeisen
etc. von innen nach außen oder, wie z.B. bei
Gußeisenrohren, umgekehrt von außen nach innen hin
aufreißt.
Nun wieder zum Ausgangspunkte dieser Untersuchung, nämlich zu den von Professor Treadwell angegebenen 41 Verhältnißzahlen zurückkehrend,
nach denen die Tension eines homogenen Rohres vom Radienverhältnisse r₁/r₀ = 5/1r₁/r₀ – 5/1 in 41 gleichweit von einander entfernten Ringschichten-Flächen bei
genügend großer innerer Pressung von der Bohrungswand an nach seiner Außenfläche hin
abnehmen soll, so würde
a) nach der ältesten hierüber oben mitgetheilten
Ansicht, jeder Elementarschicht-Fläche des Rohres immer genau dieselbe
Tension
Tn =
T₀ = Tm
zukommen müssen. – Ferner würden sich
b) nach Brix diese Tensionen
der concentrischen Rohrschalenschicht-Flächen verschiedener Radien umgekehrt
wie diese Radien selbst verhalten müssen, weil nach seiner Hypothese ganz
allgemein
T = ρ/r
E
folglich
Textabbildung Bd. 177, S. 193
ist, woraus
Tn = Tm
(rm/rn)
folgt. Weiter würden diese Tensionen
c) nach Barlow den Quadraten
der zugehörigen Radien umgekehrt proportional seyn müssen, denn da die Tensionen der
elastischen Ringschichten ihren Umfangsverlängerungen ρ/r proportional sind, also die Proportion
Tm : Tn
= ρm/rm : ρn/rm
besteht, und ferner nach Barlow's
Hypothese mit Vernachlässigung von ρ und ρ₀ gegen beziehungsweise 2r und 2r₀ auch
immer
ρ = r₀ρ₀/r
seyn muß, so hat man also die Proportion
Tm : Tn
= (r₀ρ₀)/rm² : (r₀ρ₀)/rn²,
woraus
Tn = Tm
. rm²/rn²
folgt. – Endlich ist
d) nach Lamé der
Verhältnißquotient
Textabbildung Bd. 177, S. 193
weil nach seinem Entwickelungsgange ganz allgemein:
Textabbildung Bd. 177, S. 193
ist, folglich die Proportion
Textabbildung Bd. 177, S. 193
besteht, wornach
Textabbildung Bd. 177, S. 193
gefunden wird. – Für das speciell hier vorliegende Treadwell'sche Zahlenbeispiel erhält man also, wenn in
den betreffenden Tensionsformeln nach:
1)
der alten Theorie:
Tn =
T₀
2)
der Theorie von Brix:
Tn =
Tm
rm/rn
3)
der Theorie von Barlow:
Tn =
Tm
rm²/rn² und
4)
der Theorie von Lamé:
Tn =
Tm
rm(rn +
1)/rn(rm + 1)
überall Tm = T₀ = 1000
rm =
r₀
= 1
und der Bruch 4/41 abgekürzt gleich 0,1 gesetzt wird:
1) nach der altenTheorie:
2) nach Brix:
3) nach Barlow:
4) nach Lamé:
T₀
= 1000
1000
1000
1000
T₁
= 1000
909
826
772
T₂
= 1000
832
694
722
T₃
= 1000
768
591
540
: :
:
:
:
Tn
= 1000
200
40
333
Die von Professor Treadwell mitgetheilten 41
Verhältnißzahlen für die Abnahme der
Tangentialspannungen, welche in den Wandungen eines Kanonenrohres von innen nach außen hin eintreten muß, wenn auf dessen
Seelenwand ein genügend starker Druck einwirkt – weil nämlich in diesem Falle
die elementaren Rohrwandschichten, je weiter sie nach außen
hin liegen, durch die innere Normalkraft um einen immer kleiner werdenden
Bruchtheil ihres ursprünglichen Umfangs ausgedehnt und demgemäß auch immer
weniger gespannt werden, – diese 41 Verhältnißzahlen sind demnach
der Barlow'schen Hypothese entsprechend berechnet worden.
Die nach Lamé's Formel bestimmten Zahlen derselben
Art dürften zwar wohl mehr Zutrauen verdienen und die Hypothese von Brix gibt Resultate die sowohl von Barlow als von Lamé abweichen, sich am
Schlusse aber mehr nach letzterem hinneigen; – im Allgemeinen aber dürfte mit
scharfausgerechneten Zahlenwerthen auf diesem Gebiete artilleristischen Wissens für jetzt auch wohl
überhaupt noch nicht viel zu nützen seyn, da alle bis hierher entwickelten Formeln
sich auf einen constanten Normaldruck
N₀ und auf Tangential-Tensionen
T beziehen, welche innerhalb der
Elasticitätsgrenze des Rohrmaterials liegen, die Pulverkraft aber mehr oder weniger immer stoßweise, d.h. unter Umständen mehr zerreißend als
stetig pressend wirkt und somit in einem erhöhten Grade die tangentiale
Tensionskraft des Rohrmaterials in Anspruch nimmt, was um so wichtiger ist als die
neuesten Rodman'schen Versuche über die Größe der beim
Schießen mit Pulver erzeugt werdenden Gasspannungen dargethan haben, daß dieselben
bei großen Kalibern und starken Ladungen unter Umständen den Druck von 6000
Atmosphären erreichen. – Dieses schließt jedoch den Nutzen, welchen derartige
Untersuchungen überhaupt gewähren können, keineswegs aus, und es wird z.B. bei
Reflexionen über die Frage „ob die Artillerie fernerhin, bei fortwährender
Steigerung der an ihre Wirksamkeit gestellten Anforderungen künstlicher
Metallconstructionen ihrer Kanonenrohre werde ganz entbehren können oder nicht,
und wie man eventuell dieselben am sachgemäßesten einzurichten haben
werde“ gewiß nicht unangemessen erscheinen, wenn man dabei die nach
Obigem bereits gewonnenen Untersuchungsresultate gehörig würdigt, daß
1) bei ähnlich construirten Kanonenrohren, deren
Wandstärken also nach gleichen Theilen des Kaliberdurchmessers
normirt sind, und bei gleichen
Geschoß-Anfangsgeschwindigkeiten die Cohäsionskraft der
Rohrwandungen bei großen Kalibern in einem weit höheren Grade beim Schusse in Anspruch genommen
wird, als dieses bei kleineren Kalibern der Fall ist, daß
ferner
2) bei relativer Steigerung der Wanddicken, also
Vergrößerung des Radienverhältnisses r₁/r₀ von Geschützrohren die relative Widerstandsleistung derselben – d.h. derjenige Bruchtheil
des Widerstandes gegen Längenaufreißung, welchen ein Rohr leisten würde, wenn alle
seine Wandtheilchen gleichmäßig an diesem Widerstande Theil nähmen – sehr rasch abnimmt, daß weiter
3) für Pulvergasspannungen, deren Druck pro Quadratzoll der Rohrbohrungswand den
Festigkeits Coefficienten f des Wandmaterials
überschreitet, überhaupt kein homogenes Rohr mit der ursprünglichen Spannung
seiner Theilchen gleich Null, und würde dessen Wänden auch noch so viel Metall gegeben, genügend widerstandsfähig gegen Längenaufreißung beim Schusse
dargestellt werden kann, und daß endlich
4) vermöge der specifischen Wirkungsweise des Pulvers beim
Schießen vorzugsweise immer die tangentiale Tensionskraft der Kanonenrohre in Anspruch genommen wird.
Stellt man nämlich diese Resultate der Speculation mit den beiden auf dem Gebiete der
Praxis gewonnenen, auf vorliegende Frage bezüglichen Erfahrungen zusammen, daß
einmal, wie bereits oben erwähnt wurde, bei Verwendung der
hydraulischen Pressen zu technischen Zwecken schon die Druckgrenze erreicht
worden ist, für welche homogene Wandungen, deren Theilchen vor
dem Drucke gar keiner Spannung unterliegen, und wenn man ihnen auch eine
noch so große Dicke geben wollte, nicht mehr widerstandsfähig
gegen Längenaufreißung dargestellt werden können, und daß andererseits auch
beim Schießen aus großkalibrigen Rohren und mit starken
Ladungen unter Umständen Pulvergasspannungen eintreten,
welche nach den neuesten von Rodman darüber angestellten
Versuchen sich bis zum Drucke von 6000 Atmosphären, also bis zu Pressungen pro Quadratzoll der Seelenwand steigern, welche die Minimalgrenze der absoluten Festigkeit selbst des Gußstahls
schon überschreiten, so wird man sich nicht dagegen verschließen können,
daß es jetzt sehr an der Zeit seyn dürfte eine qualitative
Verstärkung der Geschützrohrwände in künstlicher Weise auch noch dadurch zu bewerkstelligen, daß man entweder
a) den von innen nach außen aufeinander folgenden
Rohrschalen-Schichten schon gleich von vornherein
solche Spannungen gibt, daß jede derselben, beim
Schusse durch die der betreffenden Schalenschicht zukommende Ausdehnung
vermehrt, dann der an der Bohrungswand des
Rohres herrschenden Tension gleichkommt, oder aber daß
man
b) das Rohr zwar aus concentrischen Schalenschichten von ursprünglich gar keiner Spannung, diese
Schalenschichten selbst aber aus Materialien verschiedener Elasticitätskraft
bestehen läßt, welche so angeordnet sind, daß die von innen nach außen aufeinanderfolgenden Rohrschalen-Schichten ihrer
jedesmaligen Ausdehnung um eine bestimmte Länge immer einen um
so größeren Widerstand entgegensetzen, je kleiner derjenige Bruchtheil ihrer
ursprünglichen Peripherielänge ist, um welchen sie durch Ausdehnung beim Schusse an
Umfang zuzunehmen haben, oder endlich daß
c) beide Methoden dieser
künstlichen Metallconstructionen der Rohrwände miteinander
combinirt werden, indem man z.B. äußere Panzerringe von größerer
Elasticitätskraft bei ihrem Aufziehen auch noch einschrumpfen und hierbei zugleich
von innen nach außen hin sich abkühlen läßt etc. – In allen diesen Fällen
wird es endlich sehr zweckmäßig erscheinen
d) dem Material der
Rohrwandungen nach Möglichkeit eine normal zur Rohrachse peripherische Längenrichtung seiner Fibern zu geben, so daß dadurch die
einzelnen Elementar-Schalenschichten des Rohres
gewissermaßen als aus nebeneinander liegenden Drahtringen des
Rohrmaterials zusammengesetzt betrachtet werden können, welche dann einer
Tension in der Richtung ihrer Fibern, d.h. tangential zum Rohrquerschnitt, mehr
Widerstand entgegensetzen würden als einem normal gegen die Fibern gerichteten
Zuge.
Letzteres würde, insoweit es überhaupt auszuführen ist, bei der Panzerung von
Kanonenrohren um so mehr ohne Anstand geschehen können als, bei gleicher absoluter Festigkeit des Rohrmaterials nach der
Richtung seiner Fibern und senkrecht darauf, ein durch seine Wandstärke gegen
Längenaufreißung sicher gestelltes Rohr dieses dann noch um so mehr gegen
Zerreißungen in Querschnitten normal zur Seelenachse seyn würde, und zwar auch
dann noch, wenn das Rohr, wie es bei gezogenen Geschützen mit Compressivgeschoß
annähernd wirklich der Fall ist, als eine an beiden Enden verschlossene Röhre
betrachtet werden kann.
Für eine innere Gasspannung N₀ würde nämlich der
Druck auf jeden der beiden Rohrverschlüsse in einem solchen Falle, bei einem
Bohrungsradius = r, gleich r²πN₀2 r²π .
N₀, der Widerstand des Rohrmaterials von der Festigkeit f im betreffenden Querschnitte mit Beibehaltung der
bisherigen Bezeichnungen aber (r₁²
– r₀²) π f seyn, und man hat zur Bestimmung der Wandstärke für den
Gleichgewichtszustand in diesem Falle also die Gleichung:
(r₁² – r₀²) π
f = r₀² π N₀
woraus
Textabbildung Bd. 177, S. 197
folgt. – Für den Gleichgewichtsfall des
Rohrwandwiderstandes gegen Längenaufreißung des Rohres parallel zu seiner Achse
müßte, den äußeren Normaldruck N₁ vernachlässigt, nach Lamé
die Wandstärke in diesem Falle aber
Textabbildung Bd. 177, S. 198
und folglich größer als die zum Schutze gegen
Querschnitt-Abreißungen nothwendige Wandstärke:
Textabbildung Bd. 177, S. 198
seyn, was übrigens keineswegs davon abhalten mag, dem
Stoßboden des Rohres in solchen Fällen eventuell auch noch durch einige in das
Bodenstück miteingeschweißte Längenstäbe eine möglichst große Sicherheit gegen das
Abgerissenwerden zu geben.
Der Rodman'sche Kernguß mit
Abkühlung von innen nach außen hat durch das im Februar 1864 aus der
Fort-Pitt-Gießerei zu Pittsburgh hervorgegangene Riesengeschütz glänzend nachgewiesen, was eine den Forderungen 1) und 4) entsprechende künstliche
Metallconstruction der Geschützrohre zu leisten
vermag, indem dadurch ein für 100 Pfd. Pulverladung und 1000 Pfd.
Kugelgewicht bestimmtes 20zölliges Kanonenrohr mit nur 22 Zoll
starken, also kaum übergütigen Wandungen aus Gußeisen hat gebrauchstüchtig
dargestellt werden können.
Die Rohrumreifung (cerclage)
ist, wie die im Eingange dieser Abhandlung citirten früheren Referate beweisen,
schon sehr früh, seit 1830 aber wohl erst mit klarem Bewußtseyn der eigentlichen
Wirkungsweise dieses Mittels zur Erfüllung der oben angeführten Forderungen 2) und
4), beziehungsweise der Bedingungen von 1), 2) und 4) miteinander combinirt,
angewendet worden und es haben sich dabei die Erfolge dieser verschiedenen Methoden,
die Metallwand der Kanonenrohre künstlich durch Umreifung zu construiren, im
Allgemeinen immer mehr gesteigert, was aber wohl noch mehr der Fall gewesen seyn
würde, wenn man dabei in Bezug auf den Grad des
Einschrumpfenlassens der warm aufgetriebenen Panzerringe stets beachtet
hätte, daß man sich hierbei der Elasticitätsgrenze des
Rohrmaterials nicht zu sehr nähern darf, wenn die Haltbarkeit der umreiften
Rohre bei ihrem späteren Gebrauche nicht ungemein rasch abnehmen soll. –
Ingenieur-Lieutenant Treuzel sagt in seiner
obenerwähnten sehr schätzenswerthen Arbeit hierauf bezüglich, daß die Whitworth'schen Rohre den Nachtheil
eines Auftreibens der Panzer-Röhrencylinder mit der größten Spannung die
sie eben noch zu ertragen vermögen, bei längerem Gebrauche schon darthun
werden, und
Professor Treadwell's oben näher bezeichnete
Mittheilungen enthalten in dieser Beziehung die ganz bestimmte
technische Vorschrift, alle Panzerreifen in ihrem inneren Durchmesser nur eben
so viel kleiner als den äußeren Durchmesser des nächst inneren Cylinders zu
machen, daß zum Aufzuge der Panzerring niemals bis zur Aenderung seiner
gewöhnlichen Metallfarbe erhitzt zu werden braucht.
Die Drahtumwickelung endlich, welche, obgleich an sich
sehr rationell, aus den oben angeführten Gründen zur künstlichen Metallconstruction
von Geschützrohrwänden in dem bisherigen Stadium ihrer Entwickelung noch nicht
empfohlen werden konnte, sucht Professor Treadwell,
seinen neuesten obenerwähnten Vorschlägen zufolge, wenigstens annäherungsweise durch
folgende Methode der Rohrumreifung für Rohrumpanzerungen dienstbar zu machen:
Die Bildung der Panzerreifen geschieht aus Eisenplatten von angemessener Breite und
Dicke, für Reifen von 28 Zoll Durchmesser z.B. 14 Zoll breit und 1/2 bis 1 Zoll
dick, sowie einer solchen Länge, daß nach dem Aufrollen dieser Platinen Ringe von
der vorgeschriebenen Stärke entstehen. – Diese Platten werden, nachdem ihre
Enden gehörig zugeschärft worden sind, bei schwacher Rothglühhitze auf einen
cylindrischen Dorn aufgerollt, und in dieser Weise zu sogenannten Coils umgestaltet, welche dann in einem dazu passenden
Ofen bis zur Schweißhitze gebracht, über einen Dorn gesteckt und in dazu passenden
Gesenken entweder mittelst hydraulischen Drucks oder auch unter dem Dampfhammer zu
einem festen Ringe ohne Naht zusammenzuschweißen sind. Haben diese Ringe oder Reifen
sich nach ihrer Schweißung dann bis auf circa
600° Fahrenheit (315° Cels.) abgekühlt, so werden sie, über einen an
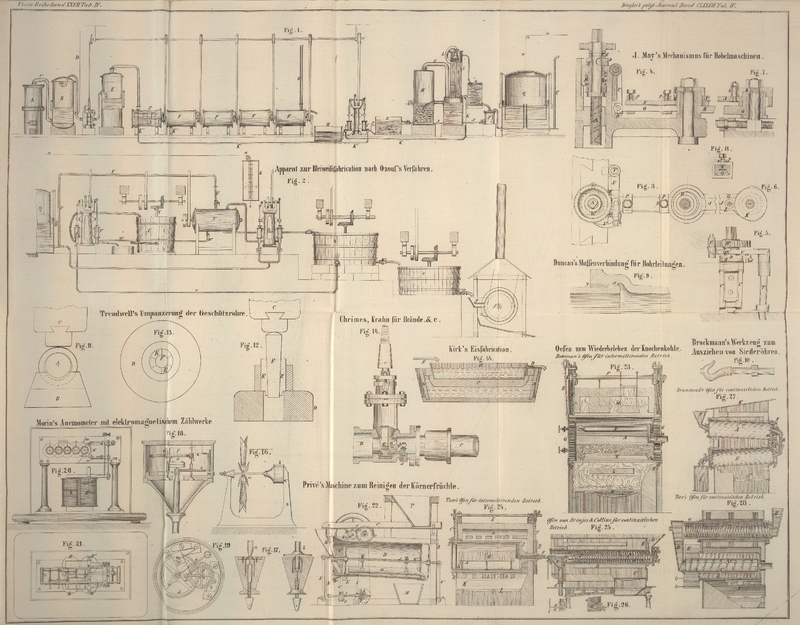
beiden Enden aufliegenden Dorn von genügender Stärke gesteckt, hierauf (Fig. 11) unter
dem Dampfhammer bis zur vorgeschriebenen Weite ausgereckt (eine Arbeit, die auch
mittelst eines Walzwerkes in der Weise geschehen kann, wie man in Deutschland
bekanntlich schon seit längerer Zeit Radreifen ohne Naht aus durchlochten
Gußstahlblöcken darstellt). Endlich werden diese Ringe, auf 200 bis 300°
Fahr. (94 bis 149° Cels.) erwärmt, auf einen ringförmigen Amboß aufgesetzt,
welcher gestattet, sie nunmehr vermittelst der in den Amboß einzusetzenden
Segmentstücke E, E (Fig. 12 und 13) und des
conischen Einsatzstempels F durch den Dampfhammer C um etwa 1/100 ihrer vorherigen Durchmesser
auszudehnen, so daß dadurch alle einander etwa widerstrebenden Tensionen ihrer
Theilchen beseitigt werden, und diese Ringe eine solche
peripherische Anordnung ihrer Fibernrichtungen erhalten, wie sie
übereinanderliegenden
Schichten von hartem Drahte, nach dem ersten Stadium seines
Ziehprocesses aufgewickelt, zugekommen seyn würde.
Cassel, im Juni 1865.
Tafeln