| Titel: | Vollkommener Centrifugalregulator; von Adrian Jacobi, Ingenieur. |
| Fundstelle: | Band 178, Jahrgang 1865, Nr. III., S. 9 |
| Download: | XML |
III.
Vollkommener Centrifugalregulator; von Adrian Jacobi,
Ingenieur.
Aus der Zeitschrift des Vereins deutscher Ingenieure,
1865, Bd. IX S. 355.
Mit Abbildungen auf Tab.
I.
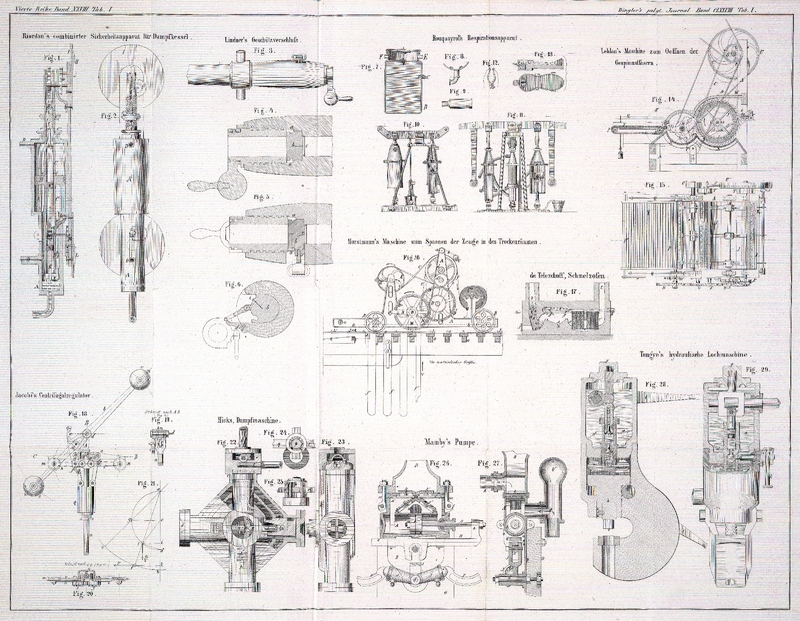
Jacobi's Centrifugalregulator.
Bei der Construction dieses Regulators ist das Gewicht der Schwungkugeln für ihre
Bewegung unwirksam gemacht, während ein besonderes Gewicht ihrer Centrifugalkraft
das Gleichgewicht hält.
Beschreibung.
Der Regulator ist in Fig. 18–20 dargestellt.
Die Regulatorwelle a trägt mittelst einer Gabel den
Schwungkugelarm b mit den gleich schweren Kugeln c, c, deren Schwerpunkte von dem Drehpunkte d des Armes b gleich weit
entfernt sind. Bei der Bewegung der Kugeln ist demnach ihre Centrifugalkraft allein
wirksam. Um den Punkt d dreht sich ferner,
gemeinschaftlich mit dem Arme b, ein an demselben
befestigtes gußeisernes Zirkelstück e, welches durch
zwei Stahlbänder mit zwei anderen Zirkelstücken f und
g, von halb so großem Radius als e, verbunden ist. Die Drehachsen dieser Zirkelstücke
werden von zwei unterhalb d an der Regulatorwelle
angebrachten Lappen aufgenommen. An den Zirkelstücken f
und g sind nun wiederum zwei gleich lange Hebel h und i so befestigt, daß
sie mit ersteren gemeinschaftlich um ihre Drehpunkte sich bewegen müssen. Diese
beiden Hebel durchlaufen daher stets einen doppelt so großen Winkel, als der Arm b, welcher vermöge der Befestigung der Hebel an ihren
Zirkelstücken einen Neigungswinkel von 45° hat, wenn die Hebel h und i horizontal stehen.
Die Enden dieser beiden Hebel tragen zwei Rollen m und
n von gleichem Durchmesser, und diese wiederum die
Schiene o, an welcher das Gewicht Q so aufgehängt ist, daß dasselbe gleichmäßig auf beide Rollen m und n sich vertheilt, und
zugleich eine Verschiebung der Schiene in ihrer Längenrichtung verhindert wird.
Aus Fig. 18
ist ersichtlich, daß das Gewicht Q den Schwungkugelarm
b der Verticalen zu nähern sucht, während die
Centrifugalkraft der Kugeln in entgegengesetztem Sinne wirkt.
Es soll nun bewiesen werden, daß, wenn man das Gewicht Q
so schwer macht, daß es bei einer bestimmten Winkelgeschwindigkeit der
Regulatorwelle in irgend
einer Stellung des Armes b der Centrifugalkraft der
Kugeln das Gleichgewicht hält, dieß auch bei jeder anderen Stellung des Armes b geschieht.
Beweis.
Da der Centrifugalkraft jeder der beiden Kugeln durch das Gewicht Q/2 das Gleichgewicht gehalten werden muß, so brauchen
wir nur die Hälfte des Armes b mit einer Kugel und einen
Hebel h in Betracht zu ziehen.
In Fig. 21 sey
ab die verticale Achse der Regulatorwelle. Man
beschreibe aus einem Punkte c dieser Verticalen mit der
Länge des Hebels h als Radius einen Kreis, welcher
dieselbe oberhalb von c in a
und unterhalb in d schneidet. Durch den Punkt a lege man ferner die Gerade ae unter einem Neigungswinkel von 45° und
die Gerade af unter beliebigem Winkel. ae schneidet den aus c
beschriebenen Kreis in g, und af denselben Kreis in l. Zieht man nun die beiden Kreishalbmesser cg und cl, so ist < gcl als Centriwinkel des Bogens gl doppelt so groß, als < gal, da derselbe Peripheriewinkel desselben Bogens
ist. Nun wissen wir aus der obigen Beschreibung des Regulators, daß der
Schwungkugelarm einen Neigungswinkel von 45° hat, während der Hebel h horizontal steht, ferner daß dieser Hebel stets einen
doppelt so großen Winkel, als der Schwungkugelarm, durchläuft; folglich muß auch der
Stellung af desselben die Stellung cl des Hebels h
entsprechen.
Wir können uns nun das Gewicht Q/2 ersetzt denken durch
eine in l angreifende, vertical nach unten gerichtete
Kraft Q/2 und dieselbe ausdrücken durch ein gewisses
Vielfaches des Kreishalbmessers ca. Der Hebelarm
der Kraft Q/2, in Bezug auf den Punkt c, ist die auf ab
gefällte Normale li. Bezeichnet man daher den
Inhalt des Dreieckes adl durch J, so hat man für das statische Moment der Kraft Q/2 den Ausdruck:
αJ,
worin α eine constante
Größe bezeichnet. Beschreibt man ferner aus dem Punkte a
mit der halben Länge des Schwungkugelarmes den Kreis bfe, auf welchem der Schwerpunkt der Kugel sich bewegt, und fällt aus f die Normale fk auf
die Drehungsachse ab, so ist die Centrifugalkraft
P der Kugel dieser Normalen proportional. Der
Hebelarm der Kraft P in Bezug auf den Punkt a ist die Kathete ak
des Dreieckes afk. Bezeichnet man daher den Inhalt
dieses Dreieckes durch J, so hat man für das statische
Moment der Centrifugalkraft den Ausdruck:
βJ
1,
worin β wiederum eine
constante Größe bedeutet. Ein Blick auf Fig. 18 zeigt nun, daß,
wenn in irgend einer Stellung des Armes b Gleichgewicht
stattfinden soll, das statische Moment des Gewichtes Q/2
halb so groß seyn muß, als das statische Moment der Centrifugalkraft einer Kugel.
Demnach hat man die Gleichung:
αJ = βJ₁/2,
woraus folgt:
J/J₁ = β/2α.
Da nun der Quotient aus den Inhalten der beiden Dreiecke adl und afk, also J/J₁, für alle Lagen des Schwungkugelarmes constant ist, so muß die
obige Gleichung auch für alle diese Lagen gelten, sobald dieß für irgend eine Lage
der Fall ist. Der Regulator ist also ein sogenannter vollkommener Regulator.
Es ist nun klar, daß einer bestimmten Winkelgeschwindigkeit der Regulatorwelle auch
ein bestimmtes Gewicht Q entspricht. Dieß Gewicht soll
daher jetzt berechnet werden.
Berechnung des GewichtesQ.
Es sey:
l die halbe Länge des Schwungkugelarmes, d.h. die
Entfernung des Schwerpunktes einer Kugel vom Drehpunkte d,
l₁ die Länge der Hebel h und i,
G das Gewicht einer Kugel,
P die Centrifugalkraft einer Kugel,
Q das zu berechnende Gewicht,
w die Winkelgeschwindigkeit der Regulatorwelle pro Secunde,
n die Zahl der Umdrehungen derselben pro Minute,
r der normale Abstand des Schwerpunktes einer Kugel von
der Rotationsachse und
g die Beschleunigung der Schwere.
Da das zu berechnende Gewicht Q unabhängig von dem
Neigungswinkel des Schwungkugelarmes ist, so können wir bei Ableitung der Formel für Q diesen Winkel beliebig, also auch gleich 45°
annehmen. Da nun der Centrifugalkraft einer Kugel durch das Gewicht Q/2 das Gleichgewicht gehalten werden soll, und dieß,
wie wir oben gesehen haben, geschieht, wenn das statische Moment des Gewichtes halb
so groß ist, als das der Centrifugalkraft, so haben wir die Momentengleichung:
rP = l₁ Q,
woraus folgt:
Q = rP/l1.
Es ist aber:
P = G/g . w²r = π²/(900 . g) .
Gn²r,
und für einen Neigungswinkel von 45°:
r² = l²/2,
so daß man erhält:
Q = (π²Gl²n²)/(1800 . gl1,)
oder wenn man l und l₁ in preußischen Fußen nimmt:
Q = (0,0001755 . Gl²n²)/l1.
Man sieht aus dieser Formel, daß bei gegebenen Dimensionen des Regulators das Gewicht
Q proportional dem Quadrate der Umdrehungszahl n ist, und daß bei gleichem Gewichte Q das Gewicht G der Kugeln
in umgekehrtem Verhältnisse zu diesem Quadrate steht.
Tafeln