| Titel: | Watzka's Umsteuerung mit variabler Expansion; mitgetheilt von J. Musy. |
| Fundstelle: | Band 179, Jahrgang 1866, Nr. XLVI., S. 172 |
| Download: | XML |
XLVI.
Watzka's Umsteuerung mit variabler Expansion; mitgetheilt von J. Musy.
Aus der Zeitschrift des österreichischen Ingenieur- und
Architektenvereins, 1865 S. 157.
Mit Abbildungen auf Tab.
IV.
Watzka's Umsteuerung mit variabler Expansion.
Die bekannten Mängel der Stephenson'schen
Coulissen-Steuerung gaben schon zu vielen neuen Constructionen
Veranlassung.
Ein im Principe sinnreich combinirter Mechanismus dieser Art wurde von Hrn. J. Watzka, Locomotivführer der österreichischen
Staatseisenbahn-Gesellschaft in Prag, erdacht, und wir verdanken es der
uneigennützigen Bereitwilligkeit des Erfinders, denselben hier mittheilen zu
können.
Die Aufgabe einer Umsteuerung für variable Expansion bei constantem Voreilen mit einem Excenter wurde von ihm durch eine Combination
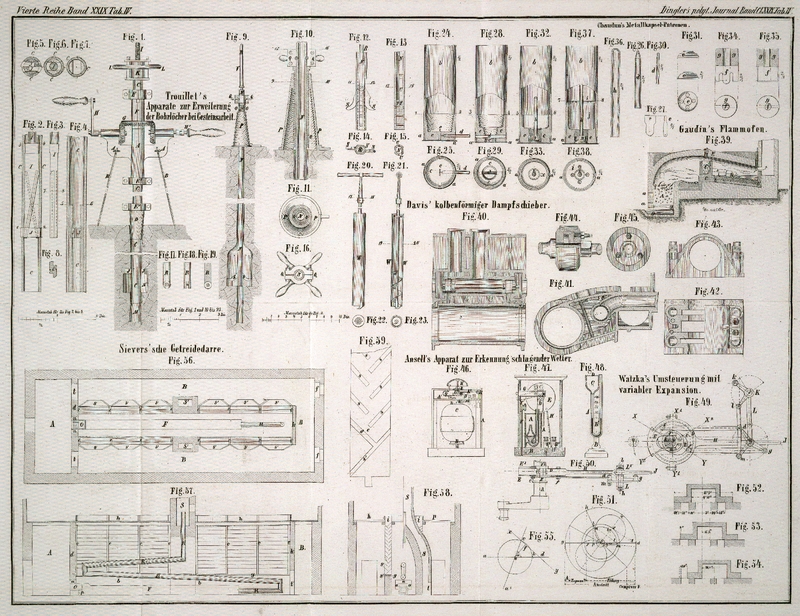
gelöst, von der die Figuren 49 und 50
eine Art der Ausführung darstellen.
A ist die Maschinenachse,
B das um 180° gegen die Kurbel o, a aufgekeilte Excenter von der Excentricität ob.
C ist eine mit einem Schlitze versehene Scheibe, welche
ihrerseits vom Ringe D der Excenterstange H umgeben ist. Das Excenter B bewegt sich im genannten Schlitze und theilt hierbei der Scheibe C sammt Ring D,
Excenterstange H und Schieberleitstange J eine hin- und hergehende Bewegung mit, indem
der Ring mittelst der zwei Chairs E, E'
und der Lineale F, G und F', G' auf der
Achse gerade geführt, der Angriffspunkt der Excenterstange h aber an den verticalen, um die Achse K
drehbaren Stangen L, L' aufgehängt ist, und daher in
einem flachen Bogen schwingt.
Zum Zwecke der veränderlichen Expansion und Umsteuerung ist die Scheibe C mittelst der beiden parallelen Stangen cd, fg
verstellbar, deren Angriffspunkte d, g zwei Enden eines
dreiarmigen Hebels d, g, m fassen, welcher um den Bolzen
h drehbar, am dritten Hebelsarm h, m durch die zum Steuerungshebel i, l führende Hängestange l,
m erfaßt wird.
K ist die Steuerungswelle; der auf derselben sitzende
Hebel i, k wird von der Zugstange erfaßt, welche zum
Umsteuerungs-Gradbogen führt.
Die Stellung xy der Mittellinie des Schlitzes
entspricht nach dem Diagramme Fig. 51 einer Füllung von
70 Proc. bei der in Fig. 49 angedeuteten Bewegungsrichtung der Kurbel; die Stellung x
₂
y₂ entspricht der entgegengesetzten
Bewegungsrichtung bei derselben Cylinderfüllung.
x₁ y₁ die verticale Stellung des Schlitzes entspricht der
Ruhestellung der gewöhnlichen Umsteuerungen, denn es geschieht hier die
Dampfvertheilung wie durch ein um 180° gegen die Kurbel aufgesetztes
einfaches Excenter, welches, wie bekannt, keine Bewegung der Maschine unterhalten
kann.
Zwischenx₁ y₁ und xy einerseits, ferner
x
₁ y₁ und
x
₂
y₂
anderseits liegen alle Admissionsgrade von 0 bis 70 Proc. für
den Vor- und Rückwärtsgang der Maschine.
Die letzt angegebene Admission ist jedenfalls die Maximalgrenze, da der Schlitz schon
eine sehr schiefe Richtung einnimmt. Eine Füllung während des ganzen Kolbenhubes ist
nach dem geometrischen Zusammenhange unerreichbar.
Theorie der Steuerung.
Es handelt sich zunächst um die Bestimmung des Schieberweges, wenn die Kurbel einen
beliebigen Winkel ω zurückgelegt hat.
Wie schon oben bemerkt, kann sich die Schlitzscheibe nur parallel in der Linie oh (Fig. 49) verschieben, so
daß der Neigungswinkel des Schlitzes constant bleibt.
Stellt nun, in Bezug auf die Figur 55, xy die Mittellinie des Schlitzes bei einer
gegebenen Stellung odx = α, oa₁ die Stellung der Kurbel,
wenn sie den Winkel aoa₁ = ω durchlaufen hat, ferner
oc = r die
Excentricität vor, so ist od die Verschiebung des
Schiebers vom Schieber-Mittel gerechnet:
od = S = of/sin α,
of = oc. cos. cof = oc . cos. (ω
– 90° + α) = r sin (α +
ω) = r sin α cos ω + r cos α
sin ω,
welcher Werth, in obige Gleichung gesetzt, gibt:
S = r cos ω + r 1/tang α sin ω. . . . (1)
Diese Gleichung ist von der allgemeinen Forms = A cos ω + B sin ω, wobei A = r, B = r/tang α
ist.
Es lassen sich daher die Schieberwege nach dem bekannten
Zeuner'schen Kreisdiagramme als Sehnen eines Kreises betrachten, dessen
Mittelpunkt-Coordinaten (Fig. 51):
oa = A/2 = r/2 und
ab = B/2 . r/2 .
1/tang α sind, und dessen Radius
Textabbildung Bd. 179, S. 174
Beschreibt man aus dem Mittelpunkt c drei Kreise mit den
Halbmessern:
om
= r = der Excentricität,
ol
= e = der äußeren Deckung, und
oq
= i = der inneren Deckung,
so kann man die Dampfvertheilung durch alle Phasen
verfolgen.
Aus Obigem ersieht man, daß die Abscisse der Schieberkreis-Mittelpunkte
unabhängig von der Füllung für alle Schieberkreise constant und gleich der halben
Excentricität ist. Es werden sich daher alle Schieberkreise in
dem Punkte
m (Fig. 51) schneiden, was das constante Voreilen dieser Umsteuerung
beweist.
Der Maximal-Schieberweg tritt für ω = 90
– α ein, und beträgt daher nach Gleichung
(1):
S max = r sin α + (r cos α)/(sin α) .
cos α = r/sin α.
Die größte Oeffnung für die Einströmung ist:
r/sin α
– e,
und für die Ausströmung:
r/sin α
– i.
Der Schieberweg für den todten Punkt ist: r –
e.
Wie schon Eingangs erwähnt, hängt die Admission von dem Neigungswinkel α des Schlitzes ab.
Die Einströmung hört auf, sobald der Schieberweg gleich der äußeren Deckung, also S₁ = e wird. Setzen
wir diesen Werth in Gleichung (1) und suchen tang
α, so folgt:
tang α = (r sin ω₁)/(e – r cos ω₁).
In Bezug auf Fig.
51 ist ω₁ = hod, ferner:
kp = pl
tang klp,
Textabbildung Bd. 179, S. 175
Es ist dem zu Folge der Winkel
α = Winkel klp.
Diese letzte Relation gibt eine sehr einfache Verzeichnungsmethode des Diagrammes.
Man mache df/dg
= m = dem Expansionsverhältnisse, ziehe die Senkrechte
fh, verbinde h mit
o, so erhält man den Durchschnittspunkt k und durch Verbindung mit l
den Neigungswinkel α. Man errichte ferner aus o auf kl die
Senkrechte oc, in welcher der
Schieberkreis-Mittelpunkt liegt. Durch s eine
Parallele st zu kl gibt ot als
Schieberkreis-Durchmesser.
Dem Diagramme auf Fig. 51 liegen folgende Daten zu Grunde:
Excentricität
r
= 16''',5
äußere
Deckung
des
Schiebers
e
= 14''',5
innere
„
„
„
i
= 3'''
lineares Voreilen des Schiebers
r–e
= 2'''.
Die übrigen Verhältnisse ergeben sich aus Fig. 52.
Bei 70 Proc. Cylinderfüllung beträgt der Winkel α
35° 37'; die größte Oeffnung für die Einströmung 13''',9.
Bei 50 Proc. Cylinderfüllung ist α = 48°
41', die größte Oeffnung für die Einströmung 7''',5.
Bei 40 Proc. ist α = 62° 26', die größte
Oeffnung 4''',1.
Diese Mittheilungen dürften genügen, um das Verdienst der dargestellten
Steuerungs-Construction in das richtige Licht zu stellen.
Es wird nämlich mit Hülfe bloß eines Excenters eine
Schieberbewegung erzielt, welche vollkommen gleich für den Vor- und
Rückwärtsgang der Maschine ist, und ein symmetrisches Oscilliren des Schiebers um
seine Mittelstellung im Gefolge hat.
Wird von den Störungen abgesehen, welche von der Kürze der Leitstange herrühren, so
erfolgt die Schieberbewegung mit mathematischer Schärfe nach dem oben verzeichneten
Diagramm; denn die Verdrehung des Schlitzes kann während eines ganzen Schieberhubes
sogar bei verhältnißmäßig geringer Länge der Excenterstange und Hängestangen L, L₁ kaum 3/4 Grad betragen, und ist daher in
der Praxis nicht wahrnehmbar.
Den Nachtheil der geringeren Eröffnung der Einströmungscanäle für höhere Expansionen
theilt diese Anordnung übrigens mit allen nur durch einen Schieber continuirlich
bewegten Steuerungen.
Das constante Voreilen für alle Expansionsgrade ist in der Construction selbst
begründet.
Die Schieberbewegung ist nahezu unabhängig von der Länge der Excenterstange, ein
Umstand, welcher diese Steuerung wesentlich zu ihrem Vortheile von der Stephenson'schen unterscheidet.
Für solche Fälle, bei welchen der Vor- und Rückwärtsgang gleich wichtig ist,
wie bei Fördermaschinen, oder woselbst möglichst kurze Excenterstangen Bedingung
sind, wie bei vielen Schiffsmaschinen, dürfte eine Construction nach Art der oben
beschriebenen sehr gute Dienste leisten.
Es läßt sich wohl kaum verkennen, daß die Reibung im Schlitze eine bedeutende werden
kann; wir zweifeln indessen nicht, daß es dem praktischen Sinn des Hrn. J. Watzka, welcher bereits eine andere sinnreiche
Verbesserung an Dampfmaschinen angegeben hat, gelingen wird, auch diesen Nachtheil
seiner Construction zu beseitigen. Indem wir diese Steuerung hiemit den Fachgenossen
zur Erprobung empfehlen, können wir schließlich nicht umhin, Hrn. Watzka unsere volle Anerkennung auszudrücken.
Tafeln