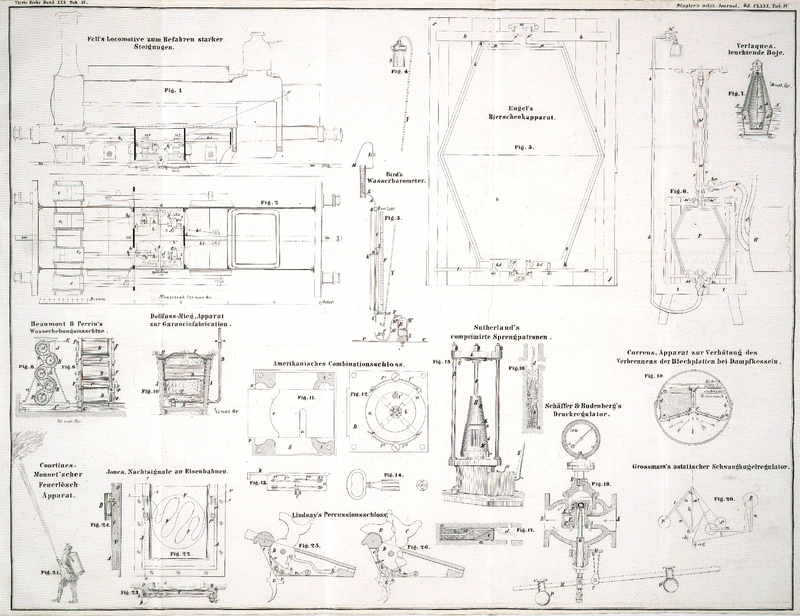
| Titel: | Der asiatische Schwungkugelregulator von Dr. Großmann in Berlin. |
| Fundstelle: | Band 180, Jahrgang 1866, Nr. XLI., S. 176 |
| Download: | XML |
XLI.
Der asiatische Schwungkugelregulator von Dr.
Großmann in
Berlin.
Aus den Verhandlungen des Vereins zur Beförderung des
Gewerbfleißes in Preußen, 1865 S. 104.
Mit einer Abbildung auf Tab. IV.
Großmann's asiatischer Schwungkugelregulator.
Die Vorrichtung Großmann's, den Watt'schen Regulator angenähert astatisch zu machen, damit man ihn direct
auf die Drosselklappe wirken lassen kann, beruht auf folgenden Principien:
Es sey in Fig.
20
P das Gewicht einer Schwungkugel, vermehrt um das halbe
Gewicht einer Hängestange, l die Länge der Hängestange,
Q das Gewicht der eventuell beschwerenden Hülse,
vermehrt um das 1 1/2 fache Gewicht einer Tragstange und den Druck, welchen das
Stellzeug in seiner mittleren Stellung auf die Hülse ausübt, a die Länge einer Tragstange, α der
Ausschlagwinkel der Hängestange bei der mittleren Stellung, ω die normale Winkelgeschwindigkeit, h
die Diagonale des von den Trag- und Hängestangen gebildeten Rhombus, welche
mit der Umdrehungsachse zusammenfällt, g die
Beschleunigung der Schwere.
Die Bedingungsgleichung für das Gleichgewicht ist
P/g . ω²l² cos α = Pl + Qh/(2 cos α) oder
Q = (2 Pω²l² cos² α)/gh – (2 Pl cos α)/h
Ferner ist
h
=
2a cos α
(1)
Q
=
(Pω²l² cos α)/ga – Pl/a
(2)
Hieraus bestimmt sich zunächst Q. Bringen wir die
Gleichung (2) auf die Form
Pl²ω²/2ga² = (Pl/a + Q)/h,
so folgt, daß sich ω
gleichzeitig sowohl mit Q als mit h ändert; es seyen ΔQ und Δh, die Aenderungen von Q und h. Soll demnach für verschiedene
Stellungen der Kugeln, also für verschiedene Werthe von h, die Geschwindigkeit constant seyn, so muß
Textabbildung Bd. 180, S. 177
constant werden; daraus folgt
Textabbildung Bd. 180, S. 177
Diese gleichzeitige Veränderung von Q und h erreicht Großmann durch
folgende Einrichtung: An die sich drehende Hülse greift auf irgend eine bekannte
Weise das eine Ende eines Winkelhebels an, dessen Schenkel rechtwinkelig auf
einander stehen; bei dem mittleren Ausschlagwinkel sey der an der Hülse angreifende
Schenkel horizontal, der andere Schenkel dagegen vertical nach oben gerichtet. Der
horizontale Arm, welchen man zweckmäßig zugleich als einen Arm des Stellzeugs
benutzen wird, sey entweder durch ein Gegengewicht abbalancirt, oder diene zugleich
zu einer constanten Vermehrung der Größe Q durch den
Druck, den er auf die Hülse ausübt und welche in Q
eingerechnet werde. Seine Länge sey m. Der verticale,
sich nach oben etwas verjüngende Schenkel trage ein durch eine Stellschraube in
verschiedenen Höhen feststellbares Gewicht. Dieses Gewicht, vermehrt um das auf den
Schwerpunkt desselben reducirte Gewicht des verticalen Schenkels sey R, der Abstand des Schwerpunktes von R vom Drehpunkt des Hebels sey n. Durch die Stellschraube des Gewichts sey zugleich dafür gesorgt, daß in
der mittleren Stellung der Schwerpunkt und Drehpunkt in derselben Verticalen liegen.
Dieses Gewicht R übt nun bei der Ausweichung des
Apparates aus seiner mittleren Stellung einen veränderlichen Druck auf die Hülse aus
und bedingt dadurch eine Veränderung von Q. Es kommt
jetzt nur noch darauf an, die Größe R oder das Product
Rn, so zu bestimmen, daß ω constant wird.
Bezeichnet φ den Winkel, um welchen, bei einer
Bewegung der Hülse um Δh, der horizontale Arm
sich gedreht hat, so ist Δh/m = tang φ, und die
von R herrührende Veränderung des Druckes ΔQ = (Rn sin
φ)/m, also
ΔQ/Δh = (Rn cos φ)/m²,
und da auch
ΔQ/Δh = (Pl²ω²)/2ga² war:
Rn = (Pl²ω²m²)/(2ga² cos φ)
Daraus geht hervor, daß es, streng genommen, kein constantes Rn gibt, welches ω constant macht; es
wird sich jedoch zeigen, daß die Schwankungen, die im Werthe von ω eintreten, für ein constant angenommenes Rn, weit unter jeder praktisch in Betracht kommenden
Grenze bleiben. Wir bestimmen Rn für φ = 0, also
Rn = (Pl² m² ω²)/2ga² (3)
Um die Aenderungen der Geschwindigkeit zu untersuchen, bezeichnen wir die dem
Ausschlagwinkel α₁, entsprechende
Winkelgeschwindigkeit mit ω₁. Der zu α₁ gehörige Werth von φ ist gegeben durch die Gleichung:
m tang φ = 2a (cos α₁ – cos
α) (4)
Für die Geschwindigkeit ω₁ haben wir
aber
Textabbildung Bd. 180, S. 178
Ferner war Pl/a + Q = h . Pl²ω²/2ga². Diesen Werth,
sowie den oben bestimmten Werth von Rn eingesetzt,
liefert
Textabbildung Bd. 180, S. 178
Da nun φ stets ein kleiner Winkel ist, so wird
dieser Ausdruck immer sehr nahe gleich der Einheit seyn.
Beispiel. Es sey P = 25 Pfd.,
l = 24'', a = 16'', ω = 50 π/30,
α =30°, m
= 30''. Aus (1) ist h = 2,3094''; aus (2) Q =19,482 Pfd.; aus (3) Rn =
154,21 Fußpfund. Mit diesen Werthen wird nach (4) und (5) für α₁ = 10° 15° 20° 25° 30°
35° 40° 45° 50°, φ =
7°,13' 6°,5' 4°,41' 2°,28' 0'' – 2°,52'
– 6°,5' – 9°,37' – 13°,24' und ω₁/ω = 0,99950 0,99974 0,99988
0,99998 1 1,00004 1,00037 1,00158 1,00473.
Der Unterschied der größten und kleinsten Geschwindigkeiten innerhalb der Grenzen für
die Amplitude, die hier weiter gewählt sind als es in der Praxis vorkommen dürfte,
beträgt demnach noch nicht 0,5 Proc.; für Veränderungen des Winkels α zwischen 20 und 40° schwankt ω um 0,05 Procent. Betrüge das verschiebbare
Gewicht 100 Pfd. und wäre der verticale Hebelarm abbalancirt, so müßte der
Schwerpunkt des Gewichtes 1,54 Fuß über dem Drehpunkt des Hebels liegen.
Soll der Regulator für eine andere Normalgeschwindigkeit adjustirt werden, so hat man
Q und Rn zu verändern.
Die erste Veränderung bewirkt man entweder dadurch, daß man mit der Hülse ein Gefäß
zur Aufnahme von Bleistücken verbindet und dasselbe verschieden belastet, oder durch
ein verschiebbares Gewicht auf dem horizontalen Hebelarm. Die Veränderung von Rn geschieht am leichtesten durch Verschiebung des
Gewichtes R; eine Scala auf dem Arm von R und für verschiedene Geschwindigkeiten normirte
Zusatzgewichte von Q würden die Adjustirung in wenig
Minuten gestatten. Die Empfindlichkeit des Regulators, welche durch die
Reibungswiderstände, die der Verschiebung der Hülse entgegen wirken, bedingt ist,
wird durch die beschriebene Einrichtung nicht wesentlich beeinträchtigt; denn zu der
Reibung, welche von den übrigen Theilen des Regulators und des Stellzeugs herrührt,
kommt nur noch die auf die Hülse reducirte, durch das Gewicht und den verticalen Arm
verursachte Zapfenreibung hinzu. Diese ist, wenn G das
Gewicht, d den Durchmesser des Zapfens und μ den Reibungscoefficienten bezeichnet μG(d/2m), ein Werth, welcher im Verhältniß zu den übrigen
Widerständen immer nur klein ausfallen kann.
Endlich dürfte es noch als ein Vorzug der angegebenen Einrichtung zu betrachten seyn,
daß dadurch ein schon vorhandener gewöhnlicher Watt'scher
Regulator sich mit Leichtigkeit in einen astatischen verwandeln läßt.
Tafeln