| Titel: | Ueber einen verbesserten Centrifugal-Regulator von J. Geiger in Lille und einige andere Verbesserungsvorschläge zu demselben Mechanismus; von G. Decher. |
| Autor: | Georg Decher [GND] |
| Fundstelle: | Band 187, Jahrgang 1868, Nr. XIX., S. 89 |
| Download: | XML |
XIX.
Ueber einen verbesserten
Centrifugal-Regulator von J.
Geiger in Lille und einige andere
Verbesserungsvorschläge zu demselben Mechanismus; von G. Decher.
Mit Abbildungen auf Tab.
II.
Decher, über Geiger's verbesserten Centrifugal-Regulator und
einige andere Verbesserungsvorschläge zu derselben Mechanismus.
I.
Es ist längst erkannt worden, daß der einfache Centrifugal-Regulator, dessen
Kugeln sich in Bezug auf die verticale Umdrehungsachse in festen Kreisen bewegen,
nicht geeignet ist, die an ihn gestellte Forderung, die
Geschwindigkeit einer Dampfmaschine und der von ihr in Bewegung gesetzten
Arbeitsmaschinen auf einer normalen Größe zu erhalten, mit hinreichender
Annäherung zu erfüllen, weil bei wachsender oder abnehmender Arbeit auch die Arbeit
des Dampfes vermehrt oder vermindert werden muß, wenn die Geschwindigkeit der
Maschine dieselbe bleiben soll, und weil diese Aenderung der Dampf-Arbeit
eine Aenderung in der Stellung der Dampfzulassungsklappe (des sogenannten
Drosselventils)Besser, weil ökonomischer im Verbrauch des Dampfes, welcher besonders am
Anfang des Kolbenhubes nur bei vollständiger Oeffnung der Klappe seine
größte Wirksamkeit äußern kann, wäre eine Aenderung in der Stellung des
veränderlichen Expansionsschiebers, die aber allerdings eine größere Kraft
von Seite des Regulators in Anspruch nähme, als die Drehung der
Drosselklappe., folglich auch eine Aenderung in der Ausweichung der Regulator-Kugeln
bedingt, während bei dem einfachen Centrifugal-Regulator einer anderen
Ausweichung der Kugeln auch eine andere Umdrehungsgeschwindigkeit für den
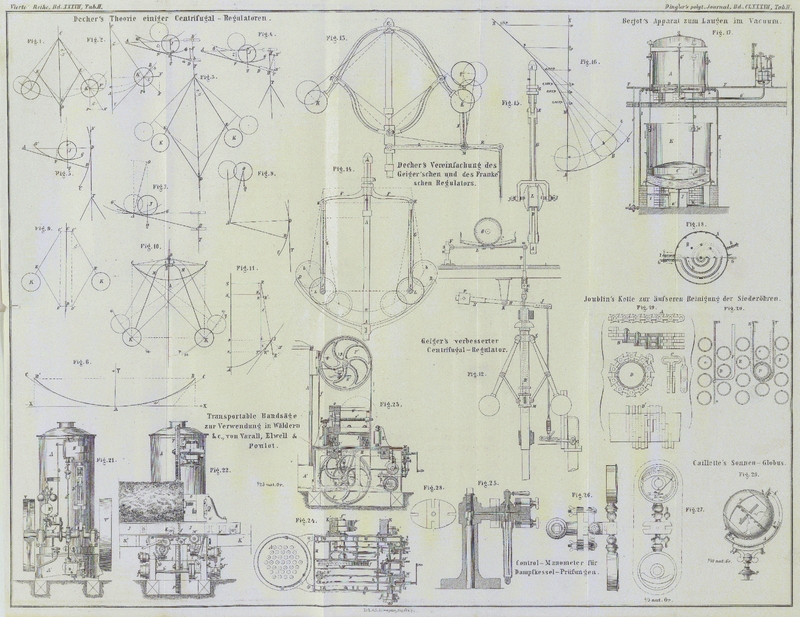
Beharrungszustand entspricht. Denn bewegen sich die Kugeln K des Regulators Fig. 1 in Kreisen um C, so kann der Beharrungszustand nur eintreten, wenn die
Resultirende N aus dem verticalwirkenden Gewicht P und dem horizontalwirkenden Bewegungsdruck F mit der Verlängerung des Halbmessers CK zusammenfällt, wenn man also hat:
F = P tang
ϑ.
Es ist aber, wenn φ die Winkelgeschwindigkeit des
Regulators um die verticale Drehungsachse AC, a den
Halbmesser CK und g die
Beschleunigung des freien Falles bezeichnet,
F = P/g a
φ² sin ϑ, folglich a/g φ² cos
ϑ – 1 =
0 (1)
die Bedingungsgleichung für den Beharrungszustand des
Regulators. Diese Gleichung setzt zwischen der Ausweichung ϑ und der Winkelgeschwindigkeit φ eine einzige nothwendige Beziehung fest, und nach dieser
entspricht einem anderen Werth von ϑ ein anderer
von φ, also einer anderen Stellung der Kugeln
nothwendig auch eine andere Umdrehungsgeschwindigkeit.
Um die Aenderung oder den Fehler in der Umdrehungsgeschwindigkeit zu berechnen,
welcher durch eine andere Stellung der Kugeln veranlaßt wird, sey α der Werth von ϑ, welcher in Gleichung (1) der normalen Geschwindigkeit φ entspricht, und φ + Δφ die
Umdrehungsgeschwindigkeit für irgend eine andere Ausweichung ϑ; man hat dann nach (1)
a/g φ² cos α – 1 = 0 und a/g (φ + Δφ)² cos ϑ
– 1 = 0, (2)
und daraus folgt sofort
Textabbildung Bd. 187, S. 90
Tritt demnach bei der Ausweichung ϑ = α ± δ ein neuer Beharrungszustand ein, so ergibt sich
für diesen ein relativer Fehler:
Textabbildung Bd. 187, S. 90
in der Umdrehungsgeschwindigkeit, welcher für + δ oder die größere Ausweichung der Kugeln
positiv, für – δ oder die kleinere
Ausweichung negativ ist. Für α = 30° und
δ = ± 10° z.B. hat man
Textabbildung Bd. 187, S. 90
im ersten Falle also eine um 6 1/3 Proc. zu große, im zweiten
eine um 4 Proc. zu kleine Umdrehungsgeschwindigkeit.
Die Verschiedenheit der absoluten Größe dieser Fehler für gleiche, aber positive und
negative Abweichung von der normalen Lage hängt mit einem ähnlichen Unterschied in
der Größe der Verschiebung der Hülse D zusammen, von
welcher eigentlich die Stellung der Dampfklappe regulirt wird; denn nimmt man das
Knie CED
Fig. 1
gleichschenkelig an, und bezeichnet die Länge der Stelze ED = CE mit b, die
Verschiebung DD' mit z, so ist
z = 2b
(cos α – cos
ϑ) = 2b (cos
α – cos (α ± δ)),
und für die obigen Werthe von δ ergibt sich
z = + 0,200 b und z = – 0,147 b;
wenn die negative Verschiebung so groß werden sollte als die
positive, so müßten die Regulatorkugeln auf 15° zusammenfallen, oder um
15° aus der normalen Lage zurückgehen; damit würde dann der entsprechende
Geschwindigkeitsfehler Δφ/φ auf
0,0532 oder 5 1/3 Proc. steigen.
Aus diesen Beispielen ersieht man zugleich, wie der Fehler in der
Umdrehungsgeschwindigkeit mit der Abweichung δ
aus der normalen Lage wesentlich kleiner wird. Man könnte deßhalb die Grenzen für
diese Abweichung δ allerdings so eng ziehen, daß
die Geschwindigkeit der Arbeitsmaschinen, welche für keine Art von Arbeit so sicher
und nothwendig bestimmt ist, daß sie nicht die geringste Aenderung erleiden dürfte,
sich nur innerhalb zulässiger Grenzen ändern könnte; dadurch würde aber auch die
Verschiebung der Hülse D ohne eine übermäßige
Vergrößerung des Regulators sehr klein ausfallen, und die Widerstände, welche sich
der Uebertragung der Bewegung der Hülse auf die Drosselklappe entgegenstellen,
würden wesentlich vergrößert, weil diese letztere auch für jene kleine Abweichungen
δ immer eine Drehung von 90° machen
muß; der ganze Regulirungsapparat würde deßhalb auch weniger empfindlich, d.h. es
bedürfte doch wieder größerer Geschwindigkeitsänderungen, um jene Widerstände zu
überwinden.
Soll demnach den Anforderungen an den Centrifugal-Regulator vollständig Genüge
geleistet werden, so muß er so umgeändert werden, daß die Bedingungsgleichung für
seinen Beharrungszustand außer der Winkelgeschwindigkeit φ wenigstens noch zwei Veränderliche enthält, die unter sich in
einer besonderen Beziehung stehen, so daß jene Bedingungsgleichung für dasselbe φ durch verschiedene Werthe der beiden anderen
Veränderlichen befriedigt werden kann.
II.
Die natürlichste und vom theoretischen Standpunkt wenigstens einfachste Lösung der
Aufgabe, einen genauen Centrifugal-Regulator herzustellen, besteht offenbar
darin, die Curve zu suchen, in welcher sich die Mittelpunkte der Regulatorkugeln
bewegen müssen, damit für jede Lage derselben der Beharrungszustand für die normale
Winkelgeschwindigkeit φ statthaben kann. Diese
Curve ist die gemeine Parabel; denn bewegt sich der Mittelpunkt K einer Kugel des Regulators Fig. 2 statt in dem Kreise
ab um C in der
Curve AB (wozu dann C
verschiebbar werden müßte), so muß nun für den Beharrungszustand derselben die
Resultirende aus dem Gewichte P und dem Bewegungsdruck
F normal zu dieser Curve seyn: bezeichnet also τ den Winkel zwischen der Tangente an derselben
in K und der verticalen Achse AC, so hat man
F tang τ = P,
und daraus folgt, wenn AC
als x-Achse genommen wird, womit sich
a sin ϑ = y, F = P/g y
φ², tang τ = dy/dx
ergibt, die Differentialgleichung der gesuchten Curve:
φ²y dy/dx
= g;
die Gleichung dieser Curve selbst ist demnach
y² = 2g/φ², (3)
d. i. die einer Parabel mit dem Parameter p = g/φ².
Den nach dieser Curve benannten parabolischen
Centrifugal-Regulator hat in Deutschland zuerst Franke in Vorschlag gebracht und ausgeführt (polytechn.
Journal, 1848, Bd. CVIII S. 321); seine Construction desselben dürfte jedoch kaum
eine glückliche zu nennen seyn, sie scheint sich wenigstens bis jetzt bei den
Maschinenbauern keiner besonderen Gunst erfreut zu haben. Ob daher die Construction,
welche ich weiter unten in Vorschlag bringen werde, trotz ihrer Einfachheit und
sonstigen praktischen Vorzüge vor anderen Verbesserungen des einfachen
Centrifugal-Regulators mehr Glück haben wird, muß einstweilen dahin, gestellt
bleiben.
III.
In Frankreich scheint man sich mehr der Ansicht zuzuneigen, daß der
Centrifugal-Regulator mit festen Drehungspunkten beizubehalten und bezüglich
seiner Wirkung durch Einführung einer neuen, veränderlichen Kraft, z.B. eines
veränderlich wirkenden Gewichtes oder einer Feder, zu verbessern sey. Eine derartige
Verbesserung ist die von Hrn. J. Geiger in Lille
ausgeführte, welche im Bulletin de la Société
industrielle de Mulhouse, t. XXXVII p. 390
(September 1867) mitgetheilt wird.
Diese Construction besteht in einem Hebel L, Fig. 12,
welcher sich um einen festen Punkt F dreht und mittelst
der verticalen (?) verstellbaren Stelze T, mit welcher
er durch ein Gelenk m verbunden ist, auf die (in der Achse der verticalen
Welle herabgehende) Schieberstange R und die bewegliche
Hülse M eines gewöhnlichen Centrifugal-Regulators
drückt. Auf diesem Hebel L ist ein Bogen C von Flacheisen, in der Mitte seiner Breite mit einer
aufwärts vorspringenden Rippe versehen, aufgeschraubt, und auf dieser stützt sich
ein bewegliches Gewicht G in der Form eines Cylinders
mit gewölbten Boden, in dessen Mantelfläche eine jener Rippe entsprechende Nuth
eingedreht ist, und welcher daher auf dem Bogen C von
einer mittleren Lage aus vor- oder rückwärts rollt, je nachdem die Hülse M sinkt oder steigt. An der Welle K, welche durch den Hebel H mit der
Schieberstange R, durch den J mit der Dampfklappe in Verbindung steht und auf diese die Bewegung der
Regulatorhülse M überträgt, ist noch ein dritter Hebel
N angebracht, und auf diesem ein verschiebbares
Gegengewicht P gegen den Läufer G mittelst einer Stellschraube befestigt.
Nach dieser Beschreibung und der beigegebenen Zeichnung wird man die Wirkung des so
verbesserten Regulators leicht erkennen. Wenn der Widerstand der Arbeitsmaschine
wächst und in Folge dessen die Umdrehungsgeschwindigkeit des Regulators abnimmt, so
sinken die Kugeln und die Hülse M, die Dampfklappe
öffnet sich und die dadurch vergrößerte Arbeit des Dampfes strebt wieder die
Geschwindigkeit der Maschine und des Regulators zu beschleunigen; mit dem Sinken der
Hülse M neigt sich aber zugleich der Hebel L abwärts, der Läufer G
rollt vorwärts und übt nun einen größeren Druck auf M
aus als vorher, und zwar, wenn der Bogen C richtig
gekrümmt ist, einen solchen, daß die Kugeln sich erst wieder heben können, wenn die
Umdrehungsgeschwindigkeit größer als die normale geworden. Ist dieses eingetreten,
so schließt die sich hebende Hülse M die Dampfklappe,
der Läufer G rollt zurück und wirkt nun zu Gunsten des
Bewegungsdruckes und zum Nachtheil des Gewichtes der Schwungkugeln, und diese können
erst wieder sinken, wenn die Umdrehungsgeschwindigkeit etwas kleiner als die normale
geworden ist. Und so würde, wenn kein Widerstand gegen die Bewegung der Hülse und
der Kugeln vorhanden wäre, bei einem constanten vermehrten Arbeitswiderstand die
abwechselnd sinkende und steigende Bewegung der Hülse in immer kleiner werdenden
Oscillationen fortdauern, bis die Kugeln des Regulators wieder bei der normalen
Umdrehungsgeschwindigkeit einen Beharrungszustand erreicht haben, in welchem der
Bewegungsdruck dem Gewicht der Kugeln und dem Druck des Läufers G auf die Hülse M das
Gleichgewicht hält, diese Hülse aber einen tieferen Stand als den normalen einnimmt,
und die Dampfklappe mehr geöffnet ist. Da aber jener Widerstand gegen die Bewegung
der Hülfe wirklich
vorhanden ist, so wird die wirkliche Umdrehungsgeschwindigkeit, mit welcher die
Kugeln in einer constanten Lage gegen die verticale Umdrehungsachse verharren, um
einen solchen Theil Δ'φ von der normalen
φ abweichen, als nöthig ist um den
betreffenden Widerstand zu überwinden, wie die Angabe einer zur Ruhe gekommenen
Waage um so viel von dem richtigen Gewicht differiren wird, als man in der
Gewichtsschale zulegen kann, ohne die Waage in Bewegung zu setzen. Wie es daher für
eine gute Waage nicht genügt, daß sie in ihren Verhältnissen richtig construirt ist,
so genügt es auch für einen guten Regulator nicht; dieser muß vielmehr wie jene
einen gewissen Grad von Empfindlichkeit besitzen, d.h.
durch eine hinreichend kleine Aenderung der Umdrehungsgeschwindigkeit von irgend
einem Beharrungszustand aus in Bewegung gesetzt werden.
IV.
Was nun zuerst die richtige Construction des Geiger'schen
Regulators betrifft, so beruht diese wesentlich auf der richtigen Krümmung der Bahn
des Läufers G, und diese läßt sich leicht auf
elementarem Wege finden (wie es Hr. Geiger wahrscheinlich
bei den bereits ausgeführten Regulatoren gethan hat), indem man für angenommene
Lagen der Kugeln den zur Herstellung des Beharrungszustandes nothwendigen Druck auf
die Hülse M und daraus die entsprechende Lage des
Läufers G auf dem entsprechend geneigten Hebel L berechnet; für jede solche Lage muß die Normale zur
Bahn vertical seyn; werden dann alle diese Normalen auf die horizontale Lage des
Hebels zurückgeführt, so läßt sich von ihren aufeinanderfolgenden
Durchschnittspunkten aus der Bogen C leicht aus
Kreisbogen zusammensetzen.
Es bietet aber auch, wie ich sogleich zeigen werde, die mathematische Bestimmung der
Gestalt des Bogens C unter einfachen Voraussetzungen
keine besonderen Schwierigkeiten, und wenn die unserem Originalbericht beigefügte
„Theorie des Geiger'schen
Regulators“ nicht ganz glücklich ausgefallen ist, so liegt die
Ursache darin, daß sich deren Verfasser (Hr. J. F. Hoppe)
durch die Beschreibung und Zeichnung dieses Regulators zu einer falschen Annahme
verleiten ließ, welche die mathematische Durchführung erschwerte. Nach jener
Beschreibung und Zeichnung soll nämlich das bewegliche Ende des Hebels L mit dem verticalen Stab T
durch einen Gelenkbolzen m verbunden seyn, sich also
auch in einer Verticalen bewegen (was offenbar unmöglich ist) und demgemäß findet
Hr. Hoppe für den Druck N des
Läufers auf die Hülse M, wenn sein Gewicht = Q, der horizontale Abstand Ax' seines Schwerpunktes J
Fig. 3 vom Drehungspunkt A des Hebels = x' und die
Länge des letzteren = l ist, den Werth: N = Q x'/l' und für die
Beziehung zwischen dem Neigungswinkel ζ des
Hebels und der verticalen Verschiebung z der Hülse M die Gleichung: z = l tang ζ, welche sich aber mit dem Werthe von N auf keine Weise vereinigen läßt.
Wenn der Drehungspunkt A des Hebels fest seyn soll, so
muß die Verbindung seines beweglichen Endes mit der verticalen Stange T eine veränderliche seyn, entweder durch eine um einen
Punkt in T bewegliche Stelze, oder so, daß sich ein
cylindrischer Bolzen B des Hebels AB
Fig. 3 in
einem mit T verbundenen horizontalen Schlitze ab, oder ein solcher Bolzen D
Fig. 4 der
Stange T in einem Schlitze BC des Hebels ABC bewegt, oder so, daß
die gezahnte Stange T, Fig. 5, in einen gezahnten
Bogen CD am Ende des Hebels AB eingreift, u.s.f. Alle diese Verbindungsarten,
und selbst die, bei welcher L und T durch einen gemeinschaftlichen Gelenkbolzen verbunden sind, wie in Fig. 12, wobei
aber der Drehungspunkt F mit einer Stelze um einen
anderen, festen Punkt beweglich ist, geben bei einer geringen Neigung des Hebels für
die Sache selbst ziemlich unbedeutende, für die mathematische Theorie dagegen sehr
erhebliche Unterschiede. Lassen wir die zuletzt genannte und die erste der vier
vorher aufgezählten Verbindungsarten als die complicirteren für die Theorie bei
Seite, und beschränken wir uns demnach auf die in den Figuren 3, 4 und 5 dargestellten
Verbindungen zwischen AB und T, so haben wir folgende leicht abzuleitende,
zusammengehörige Werthe,
für Fig.
3: N = Q x'/l
cos ζ, z = l sin
ζ,
für Fig.
4: N = N₁ cos ζ = Q x'/l cos²
ζ, z = l tang
ζ,
und
für Fig.
5: N = Q
x'/l', z =
lζ,
also je für N und z ganz verschiedene Formen, welche, wenn sie auch für
kleine Werthe von ζ im Werthe nahe
übereinstimmen, doch sehr verschiedene Gleichungen für die gesuchte Curve geben, und
von denen kein Paar mit dem von Hrn. Hoppe angenommenen
übereinstimmt.
Außerdem sind aber in Betreff jener Beschreibung und der Theorie des Hrn. Hoppe noch folgende Bedenken zu erheben. Wenn in der
Beschreibung des Geiger'schen Regulators, Fig. 12, das Gewicht P als ein Gegengewicht gegen den Läufer G angegeben wird, so wäre das doch eine sehr
überflüssige Verschwendung schwerer Massen, die sicher nicht zur Vermehrung der Empfindlichkeit des Regulators beitragen würde, und es wäre doch gewiß
einfacher, den Läufer um so viel leichter zu machen, daß das Gewicht P entbehrt werden könnte. Es kann daher dieses Gewicht
P nur als Gegengewicht für den ganzen
Steuerungs-Apparat der Drosselklappe aufgefaßt werden, dazu bestimmt, den
Druck dieses Apparates auf die Hülfe M aufzuheben; aber
selbst das wäre bei dem Geiger'schen Regulator nicht
streng nothwendig. – Und wenn dann Hr. Hoppe mit
P'
„die Summe aller anderen Kräfte (außer dem Gewichte der Schwungkugeln und
des Läufers G), welche die
Hülse überwinden muß, um sich zu erheben,“ worunter also
außer jenem Gegengewicht P der Reibungswiderstand zu
verstehen ist, in die Bedingungsgleichung für den Beharrungszustand einführt, so ist
dagegen einzuwenden, 1) daß der Reibungswiderstand für die steigende Bewegung der
Hülse abwärts, für die sinkende aufwärts gerichtet ist, und deßhalb mit doppeltem
Zeichen eingeführt werden müßte, und 2), daß es sich aber überhaupt nicht um eine
steigende oder sinkende Bewegung der Hülse handeln kann, weil diese eine Aenderung
der Umdrehungsgeschwindigkeit bedingt, sondern nur um den Beharrungszustand bei
constanter Umdrehungsgeschwindigkeit, für welchen ein Reibungswiderstand eben so
wenig in Betracht kommen kann, wie beim Gleichgewichtszustand der Waage. Dieser
Reibungswiderstand ist dagegen sehr und hauptsächlich zu berücksichtigen, wenn die
Empfindlichkeit des Regulators in Frage kommt, wie
weiter unten gezeigt werden wird.
V.
Gehen wir nun für die theoretische Bestimmung der Bahn des Läufers der größern
Einfachheit wegen von der Annahme aus, daß der Steuerungsapparat der Drosselklappe
in's Gleichgewicht gesetzt seyWenn der Steuerungsapparat auf die Hülse D, Fig. 3,
einen constanten Druck oder Zug P' ausübt, so
ist in der nachfolgenden Gleichung (4) das constante Glied Pa durch Pa ± P'b zu ersetzen., im Beharrungszustand des Regulators also nur das Gewicht und der
Bewegungsdruck der Schwungkugeln und das Gewicht des Läufers als wirksame Kräfte
auftreten, und daß die Verbindung zwischen dem Hebel und der Stange T nach Fig. 3 hergestellt ist,
und bezeichnen wir wie oben das Gewicht einer Schwungkugel mit P, das des Läufers mit Q,
die Länge der Arme CK mit a, der Stelzen ED = CE mit b, des Hebels
AB mit l, den
Neigungswinkel des letzteren gegen die Horizontale AB' mit ζ, abwärts positiv, aufwärts
negativ genommen, den Ausschlagwinkel der Arme CK
mit ϑ, die normale Winkelgeschwindigkeit des Regulators mit φ, und den horizontalen Abstand der Achse J des Läufers oder seines Berührungspunktes m auf der Curve G'FG von dem
festen Punkte A mit x', so
haben wir folgende Werthe:
1) Druck des Läufers auf den Schlitz ab oder auf
die bewegliche Hülse D:
Textabbildung Bd. 187, S. 97
2) Moment dieses Druckes in Bezug auf C nach der Theorie
des gleichschenkeligen Knie's:
Textabbildung Bd. 187, S. 97
3) Moment der beiden Gewichte P in Bezug auf C: 2Pa sinϑ,
4) Moment des Bewegungsdruckes beider Kugeln:
2 P/g
a²φ² sin ϑ cos ϑ,
und die Gleichung für den Beharrungszustand wird damit
Textabbildung Bd. 187, S. 97
Ist dann noch α der Werth von ϑ, für welchen AB horizontal, also ζ = 0 ist, und
bezeichnet x₀ den entsprechenden Werth von x', d. i. den Abstand AF, so hat man auch
Textabbildung Bd. 187, S. 97
und wenn man dann ferner beachtet, daß
2b (cos
ϑ – cos α) = z = l sin ζ,
und daß
x' = (x₀ + x) cos
ζ + y sin ζ,
wenn x und y die Koordinaten Fn und nm des Berührungspunktes m in Bezug auf AB als x-Achse und F als
Anfang sind, so folgt durch Subtraction der ersten Gleichung (5) von (4) mit der
Abkürzung:
Textabbildung Bd. 187, S. 97
die einfache Gleichung:
x + y tang
ζ – k sin ζ = 0,
welche mit den bekannten Beziehungen:
tang ζ = dy/dx, sin ζ = dy/ds = dy/dx . dx/ds
sofort in die Differentialgleichung der gesuchten Curve
übergeht, und so die Form annimmt:
x + y
dy/dx – k
dy/dx . dx/ds =
0 (7)
Diese Gleichung wird sogleich integrirbar, wenn man nur solche kleine Neigungen ζ zuläßt, daß cos
ζ = dx/ds ohne merklichen Fehler = 1 gesetzt werden kann,
und zwar findet man unter dieser Voraussetzung, und da y
mit x Null werden muß, als Integral der Gleichung
(7)
x² + y² – 2ky
= 0, (8)
also die Gleichung eines Kreises
vom Halbmesser k, dessen Mittelpunkt O natürlich in der durch F
gehenden Normalen zu AB liegen muß.
Da nun in der Anwendung die Verschiebung z der Hülse D, also auch l sin ζ
in ziemlich enge Grenzen eingeschlossen ist, so kann man der zuletzt gemachten
Voraussetzung betreffs cos ζ durch Vergrößerung
von l beliebig nahe kommen, und die durch Gleichung (8)
ausgedrückte einfache Lösung unserer Aufgabe kann für die Praxis als vollkommen
genügend betrachtet werden.
Uebrigens verursacht auch die Integration der vollständigen Gleichung (7) keine
großen Schwierigkeiten. Setzt man darin dy/dx = p, und bringt sie
so auf die Form:
x + py = k p/√(1 + p²)
nimmt dann, um x zu eliminiren,
davon die Ableitung nach x und multiplicirt diese mit
p/√(1 + p²), so ergibt sich die Gleichung:
Textabbildung Bd. 187, S. 98
aus deren unbestimmtem Integral:
Textabbildung Bd. 187, S. 98
weil p und y mit einander Null werden, sofort das bestimmte
2y √(1 + p²)³ = kp²
hervorgeht. Eliminirt man endlich zwischen dieser Gleichung
und der Gleichung (7) die Veränderliche p, so findet man
für die gesuchte Curve folgende Gleichung des 6. Grades:
4 (x² + y²)³ + k² (8y⁴ – x⁴
+ 20x²y²) +
4k⁴y² =
0. (9)
Diese Gleichung enthält nur gerade Potenzen von x und y, die entsprechende Curve ist folglich zu beiden Seiten
des Punktes F symmetrisch; sie wird nach x lösbar, wenn man sie durch Zufügung der nothwendigen
positiven und negativen Glieder zuerst auf die Form:
4 (x² + y²)(x² + y² + k²)² – 36 k²x² (x² + y²)
– 4 k²x² + 27 k²x⁴ = 0
und dann, x² + y² =r²
gesetzt, auf die Form:
27 k²x⁴ – 4 (9r² + k²) k²x² + 4r² (r² + k²)² = 0 (10)
bringt; man zieht daraus mit der Beachtung, daß r mit x Null werden muß,
Textabbildung Bd. 187, S. 99
worin ρ für r/k steht, und erkennt daraus, daß die gesuchte Curve,
obgleich sie nicht geschlossen ist, doch eine sehr beschränkte Ausdehnung hat, da
ρ nicht größer als √1/3 werden kann.
Sie hat die in Fig.
6, für k = 10 Centim. dargestellte Form, und
besteht aus zwei congruenten Zweigen, wie B'AB, welche
sich und die x-Achse in A berühren. Die Coordinaten der Endpunkte B
und B' sind
x = ± 2/9 k√6 = ± 0,544 k,
y = ± 1/9 k√3 =
± 0,192 k
und für den Winkel τ₁, welchen die Tangente in B mit
der Achse AX bildet, hat man tang τ₁ = √2, τ₁ = 54° 44'; dieß ist also auch die größte Neigung ζ, welche der Hebel AB
Fig. 3
erhalten kann.
Endlich zeigt Fig.
6, wie es sich auch aus der analytischen Behandlung ergibt, daß der in
Gleichung (8) ausgedrückte Kreis C'
AC der Krümmungskreis
unserer Curve im Punkte A ist, und bis zu einer Neigung
ζ = τ =
18° noch sehr nahe mit derselben zusammenfällt; denn es beträgt dort der
Unterschied zwischen den Ordinaten der Curve und des Kreises nur 0,0013 k. Man erhält demnach eine für das praktische Bedürfniß
vollkommen genügende Annäherung, wenn man bei Anwendung dieses Krümmungskreises den
Hebel AB wenigstens 5 mal so lang nimmt als die
ganze Verschiebung der Hülse D, man hat dann für den
größten Werth ζ₁ von ζ die Beziehung: sin
ζ₁ = 0,1, und darnach wird cos
ζ₁ = 0,995 und ζ₁
nicht ganz 6°. Diese Annäherung, welche ich später für einen besonderen Fall
noch näher erörtern werde, wird um so mehr genügend erscheinen, wenn man beachtet,
daß die Empfindlichkeit des Regulators doch auch eine
beschränkte ist, und deßhalb kleine Abweichungen von der normalen Geschwindigkeit
unvermeidlich sind.
VI.
Die Empfindlichkeit eines Regulators ist zweifacher Art;
einmal soll die regulirende Hülse desselben, wie schon oben angedeutet wurde, durch hinreichend kleine
Aenderungen der Umdrehungsgeschwindigkeit vom Beharrungszustande aus in Bewegung
gesetzt werden; d.h. der Regulator soll für kleine
Aenderungen der Geschwindigkeit empfindlich seyn; dann aber soll diese Bewegung der
Hülse auch hinreichend rasch vor sich gehen im Verhältniß zu der bewegenden Kraft,
damit die Aenderungen in der Stellung der Dampfklappe mit den Aenderungen in der
Geschwindigkeit der Maschine gleichen Schritt halten; der Regulator soll also auch
für schnelle Aenderungen der Geschwindigkeit empfindlich
seyn. Die Empfindlichkeit erster Art wird hauptsächlich von den Widerständen
abhängen, welche der Bewegung der Hülse entgegenstehen, die der zweiten Art dagegen
von dem Verhältniß der zu bewegenden Massen zu der bewegenden Kraft.
Diese Bedingungen für die Empfindlichkeit wollen wir nun mathematisch ausdrücken, und
zwar zunächst für den einfachen Centrifugal-Regulator, von welchem dann
leicht zu dem Geiger'schen übergegangen werden kann. Dazu
bezeichnet
ϑ₀ die Ausweichung der Kugeln K, Fig. 1 für einen
beliebigen Beharrungszustand, in welchem die Umdrehungsgeschwindigkeit φ' der Gleichung: αφ'² cos ϑ₀
= g Genüge leistet,
ϑ die Ausweichung derselben
bei steigender Bewegung der Hülse D am Ende der Zeit t, wenn die Umdrehungsgeschwindigkeit φ' + Δt
φ' geworden ist,
ψ = dϑ/dt die
Winkelgeschwindigkeit und
M das Massemoment der Kugeln in Bezug auf den
Drehungspunkt C,
w = dz/dt die aufwärts
gerichtete Geschwindigkeit der Hülse D, und
M das Moment sämmtlicher Widerstände gegen die Bewegung
der Hülse in Bezug auf C;
vernachlässigt man dann die Massen der übrigen Theile des
Regulirungs-Apparates neben der der Kugeln, so hat man als Bewegungsgleichung
der letzteren:
2M
dψ/dt = 2 Fa cos
ϑ – 2 Pa sin ϑ –
M, (11)
worin der Bewegungsdruck F nun
durch: P/g a (φ' +
Δt
φ')² sin
ϑ zu ersetzen ist.
Es ist aber auch
z = 2b
(cos ϑ₀ – cos ϑ)
und daraus folgt
w = dz/dt
= 2b sin ϑ . ψ, dw/dt =
2b cos ϑ ψ² + 2b sin ϑ dψ/dt;
nimmt man nun daraus den Werth von dψ/dt und setzt ihn in (11) ein, so ergibt sich die
Bewegungsgleichung der Hülse D in der Form:
Mdw/dt = 2M
bψ² cos
ϑ + b sin ϑ (2 Fa cos ϑ – 2 Pa sin
ϑ – M), (12)
und aus ihr ziehen wir die Bedingungen für beide Arten der
Empfindlichkeit des Regulators durch folgende Erwägungen:
1) die steigende Bewegung der Hülse und der Kugeln beginnt vom Beharrungszustande an
jedenfalls mit der Ausweichung ϑ₀, und den
Geschwindigkeiten w₀ = 0, ψ₀ = 0; es kann also keine solche Bewegung eintreten, bis
der Factor 2 Fa cos ϑ – 2 Pa sin ϑ – M,
welcher im Beharrungszustande wegen der Bedingung: Fa cos
ϑ₀ – Pa sin
ϑ₀ = 0 negativ ist, durch Vergrößerung der
Umdrehungsgeschwindigkeit φ' bei der
ursprünglichen Ausweichung ϑ₀ größer als 0
geworden ist; der Anfang jener Bewegung ist demnach bedingt durch die Gleichung:
2 F₀a
cos ϑ₀ – 2 Pa sin
ϑ₀ – M₀ =
0, (13)
worin F₀ den
Bewegungsdruck: P/g a (φ' + Δ₀ φ')² sin ϑ₀ und M₀ das Moment der
Widerstände für die Ausweichung ϑ₀ und den
Anfang der Zeit t bezeichnet, und diese Gleichung wird
dazu dienen, die kleinste relative Aenderung Δ₀ φ'/φ' der Beharrungsgeschwindigkeit φ' zu bestimmen, mit welcher eine Bewegung der Hülse eintreten
kann, durch welche wir also einen Maaßstab für die Empfindlichkeit der ersten Art erhalten werden. Dazu ist aber noch das
Moment M₀ auszudrücken. Die Widerstände, welche
der Bewegung der Hülse entgegenstehen, sind doppelter Art; sie bestehen a) aus den Widerständen des Steuerungsapparates und der
Hülse selbst, und b) aus den Widerständen gegen die
steigende Bewegung der Schwungkugeln.
a) Der Gesammtwiderstand des Steuerungsapparates ist
zwar streng genommen nicht constant; man wird aber keinen großen Fehler begehen,
wenn man den Mittelwerth desselben als constant annimmt, und diesen als ein Gewicht
W einführt, das durch die ganze Bewegungshöhe der
Hülse fallend eine Arbeit leistet gleich derjenigen, welche an der Hülse (bei
weggenommenen Schwungkugeln) zur Drehung der Dampfklappe um 90° geleistet
werden muß. Dieses Gewicht W wird demnach der Bewegungshöhe der Hülse verkehrt proportional seyn,
und sein Moment in Bezug auf C ist wie das des Druckes
N in §. V = 2 Wb sin ϑ.
b) Der Widerstand gegen die steigende Bewegung der
Schwungkugeln ist wieder ein doppelter Reibungswiderstand; er besteht nämlich aus
der Reibung an den Gelenkbolzen C in Folge des von den
Kugeln auf sie ausgeübten Druckes, welcher der Resultirenden N aus dem Gewichte P und dem Bewegungsdruck
F der Kugeln gleich ist, und, nach den gewöhnlichen
Constructionen, aus der Reibung an den Backen der Gelenke C oder an einer Führung, an welcher die Arme CK gleiten können, in Folge des horizontalen Druckes, der auf die Kugeln
ausgeübt werden muß, um deren Umdrehungsgeschwindigkeit zu beschleunigen, und dessen
Moment in Bezug auf die verticale Drehungsachse dieser Beschleunigung Δt
φ' und dem Massemoment der Kugeln in Bezug auf
dieselbe Achse proportional ist. Dieser Druck selbst ist demnach dem Abstand der
gedrückten Stelle des Armes CK von der verticalen
Drehungsachse verkehrt proportional und deßhalb gar nicht unbedeutend, wenn er von
den Gelenkbacken C selbst ausgeübt werden muß; das
Moment oder die Arbeit der entsprechenden Reibung dagegen bleibt unabhängig von der
Lage der gedrückten Stelle. Denn ist m der Abstand
dieser Stelle von C, also m sin
ϑ der von der verticalen Achse, und bezeichnet M' das Massemoment einer Kugel in Bezug auf diese Achse, so wird jener
Druck = M'/(m sin ϑ)
Δt
φ'; die entsprechende Reibung, für welche der
Coefficient = f₁ sey, ist = f₁ M'/(m sin ϑ) Δt
φ', und deren Moment in Bezug auf C = f₁ M'/(sin ϑ) Δt
φ' wird abhängig von m. Diese Reibung kann dagegen wesentlich vermindert werden, wenn man statt
der gewöhnlichen Construction die Arme CK bei C mit erweiterten Gabeln versieht und die Gelenkbolzen
entsprechend verlängert; denn ist die Weite der Gabeln = 2e, so ist der von der oben erwähnten Beschleunigung herrührende Druck auf
die Gelenkbolzen = M'/2e
Δt
φ' und das Moment der entsprechenden Reibung in
Bezug auf C wird fρ/2e
M' Δt
φ', wenn ρ den
Halbmesser der Gelenkbolzen und f den Coefficient für
die Zapfenreibung bezeichnet. Dazu kommt dann aber noch die Reibung an dem einen
oder anderen Anlauf der Gelenkbolzen, deren Moment in Bezug auf C durch den Ausdruck P/g a sin
ϑ Δt
φ'. f₁ρ' gemessen wird, wenn ρ' der
von ρ wenig verschiedene mittlere Halbmesser des
Anlaufes ist. Das Verhältniß des ganzen Reibungsmomentes bei dieser Construction zu
dem bei der gewöhnlichen
Einrichtung wird daher mit Einführung des angenäherten Werthes: P/g a² sin²
ϑ für M'Strenggenommen wäre M' = P/g (a² sin² ϑ + 2/5 r₁²), wenn r₁ der Halbmesser einer Schwungkugel ist.
fρ/2e a
sin ϑ + f₁ρ' : f₁a oder fρ/2f₁e sin ϑ + ρ'/a,
also ein ziemlich kleiner Bruch, wenn e > ρ, da f₁ wenigstens = 2,5 f und a > 50 ρ'. Für e = 5ρ z.B. und mit
den Werthen f₁ = 2,5 f,
a = 50 ρ', ϑ = 30° würde
dieses Verhältniß = 1/50 + 1/50 = 1/25, d.h. der entsprechende Reibungswiderstand
gegen die Bewegung der Kugeln wäre bei der ersten Einrichtung 25 mal so groß, als
bei der letzten.
Für den Druck N auf die Gelenkbolzen C hat man
N = F sin
ϑ + P cos ϑ = P/g a (φ' + Δt
φ')² sin² ϑ + F
cos ϑ,
und das Moment der entsprechenden Reibung ist fρN; damit und mit den vorhergehenden
Reibungsmomenten wird daher entweder
Textabbildung Bd. 187, S. 103
nach der gewöhnlichen Construction des Regulators, oder
Textabbildung Bd. 187, S. 103
wenn die Arme CK bei C erweiterte Gabeln erhalten. Da nun Δ₀ φ'
gegen φ' sehr klein bleiben soll, so kann man
(φ' + Δ₀φ')² mit
hinreichender Annäherung durch φ'²+ 2φ'Δ₀φ' ersetzen; beachtet man dann noch die Bedingung für den
Beharrungszustand: aφ'²/g cos ϑ₀ = 1 und vereinigt alle mit Δ₀φ'
multiplicirten Glieder, so findet man für M₀ die
Werthe:
Textabbildung Bd. 187, S. 103
welche ich bezüglich der mit fρ multiplicirten Glieder sogleich in Zahlen ausdrücken will, um
deren relative Größe augenfällig zu machen, und zwar mit Zugrundlegung der obigen
Werthe für f, a, e und ϑ₀ und dann der weiteren ρ' = ρ, a = 0,1. g und φ' =
√(10/cos 30°) = 3,4, was einer
Umdrehungszeit von nahe 1,85 Secunden entspricht; man findet so
Textabbildung Bd. 187, S. 104
und ersieht daraus, daß in der oberen Zeile Δ₀φ'/φ' ein viel kleinerer Bruch seyn muß, wenn das damit
multiplicirte Glied neben der Einheit soll vernachlässigt werden können. Der
größeren Einfachheit wegen soll für das Folgende der Werth von M₀ durch den Ausdruck:
Textabbildung Bd. 187, S. 104
dargestellt werden, welcher je nach dem Werthe von λ auf die beiden Fälle anwendbar ist, und damit
und mit dem Werthe von F₀, dann mit der Bedingung
für den Beharrungszustand in der Form:
P/g a²φ'² sin ϑ₀ cos ϑ₀ – Pa
sin ϑ₀ = 0
nimmt die Gleichung (13) zuerst die Form an:
2 P (a
sin 2ϑ₀ – fρλ sin²
ϑ₀) Δ₀φ'/φ' = Wb sin 2ϑ₀ + 2
fρP,
und wenn man dann noch die kleinen Brüche:
Textabbildung Bd. 187, S. 104
setzt, so ergibt sich endlich der einfache Ausdruck:
Textabbildung Bd. 187, S. 104
für die kleinste relative Aenderung der
Beharrungsgeschwindigkeit φ', mit welcher eine
steigende Bewegung der Hülse beginnt.
Wenn die Hülse sinken soll, so ändern der Widerstand W
und alle mit f multiplicirten Glieder das Zeichen, und
es wird demnach
Textabbildung Bd. 187, S. 104
der Ausdruck für die relative Aenderung der
Beharrungsgeschwindigkeit, mit welcher eine sinkende
Bewegung der Hülse eintritt. In diesen Ausdrücken sind bei den gewöhnlichen Verhältnissen die
Glieder des Zählers unter sich und mit Δ₀φ'/φ' von gleicher Größe-Ordnung; das Glied
γλ sin² ϑ₀ des Nenners dagegen wird besonders bei unserer zweiten
Einrichtung des Regulators, für welche die zweite Zeile der obigen Werthe von M₀ gilt, in Bezug auf sin 2ϑ₀ von der zweiten Ordnung
seyn, und kann neben diesem vernachlässigt werden; man hat dann für die steigende
wie für die sinkende Bewegung der Hülse denselben einfachen Ausdruck:
Textabbildung Bd. 187, S. 105
da sich die gleichzeitige Aenderung der Zeichen aller Glieder
dieser Gleichung von selbst versteht; und damit ist denn auch die gesuchte Bedingung
E₁ für die Empfindlichkeit der ersten Art gefunden, aber in solcher Weise, daß diese
Empfindlichkeit zu dem Werthe von E₁ im
umgekehrten Verhältniß steht.
Wir schließen daraus, daß diese Empfindlichkeit um so größer ist, je kleiner die
Quotienten β und γ und je größer sin 2ϑ₀ ist. Soll daher die Empfindlichkeit in
der normalen Lage am größten seyn, so muß man den diese Lage bestimmenden Winkel α = 45° nehmen, und hat dann für diesen
einfach
Textabbildung Bd. 187, S. 105
Außerdem zeigen die Werthe (14) von β und γ, daß diese Empfindlichkeit hauptsächlich mit
der Vergrößerung der Länge a der Arme CK wächst, weil durch Vermehrung des Gewichtes P zwar β kleiner
wird, dafür aber der Halbmesser ρ des
Gelenkbolzens, wenn auch nur im Verhältniß der Quadratwurzeln aus P stärker werden muß, also γ größer wird. Setzt man demzufolge ρ = c √P, so erhält
Textabbildung Bd. 187, S. 105
in Bezug auf P einen kleinsten
Werth, wenn man hat
Textabbildung Bd. 187, S. 105
dieser Werth von P wäre demnach
der vortheilhafteste, und eine weitere Vermehrung der Empfindlichkeit nur durch
Vergrößerung von a zu bewerkstelligen, und man wird sich
leicht überzeugen, daß so der Werth (15) leicht viel kleiner gemacht werden kann,
als die aus (2a) sich ergebenden
Abweichungen von der normalen Umdrehungsgeschwindigkeit.
2) Die Empfindlichkeit zweiter Art, welche auch erst in
zweiter Linie zu berücksichtigen ist, bemißt sich nach dem Werth des Verhältnisses
der Beschleunigung dw/dt der Hülse zu der
beschleunigenden Ursache für den Anfang der Bewegung der Hülse oder für den Anfang
der Zeit t. Dazu bringe ich die Gleichung (12) mit den
vorhergehenden Umwandlungen zuerst auf die Form:
Textabbildung Bd. 187, S. 106
und ziehe daraus mit Einführung des constanten Factors g, welcher mit dw/dt
gleichartig ist, um überall die Verhältnißform herzustellen, das Verhältniß:
Textabbildung Bd. 187, S. 106
welches mit dem angenäherten Werth: Pa² für gM
und sec ϑ₀ für aφ'²/g für den Anfang der Zeit
t, wo ψ = 0 ist,
den Ausdruck gibt:
Textabbildung Bd. 187, S. 106
Dieser Ausdruck zeigt, daß die Empfindlichkeit zweiter
Art, welche zu dem E₂ in geradem Verhältniß
steht, bei dem einfachen Regulator mit dem Verhältniß b/a wächst und in Bezug auf ϑ₀ seinen größten Werth erreichen würde,
wenn sin ϑ₀ = 1 wäre; von dem Gewichte
oder der Masse P ist sie natürlich unabhängig, da diese
die bewegende und die bewegte ist.
VII.
Kehren wir nun wieder zu dem Geiger'schen Regulator
zurück, um die vorhergehende Untersuchung auf diesen anzuwenden, so haben wir der
Gleichung (11) für die neu hinzukommende Masse und das Gewicht Q auf der linken Seite noch ein Glied: d.M'ψ'/dt worin M' das veränderliche Massemoment und ψ' die
Winkelgeschwindigkeit des Gewichtes Q in Bezug auf den
Drehungspunkt A des Hebels AB, Fig.
3, bedeutet, auf der linken Seite das frühere Glied: 2Qb (x' sin
ϑ)/(l cos
ζ) beizufügen, und das Widerstandsmoment M noch um das Reibungsmoment in A und B zu erweitern. Die Gleichung (11) nimmt damit zuerst
die Form an:
Textabbildung Bd. 187, S. 107
da bei diesem Regulator die normale Umdrehungsgeschwindigkeit
für jedes ϑ die Beharrungsgeschwindigkeit ist,
und kommt mit der Bedingung (4) für den Beharrungszustand auf die einfachere
Gleichung:
Textabbildung Bd. 187, S. 107
zurück, aus welcher sich für t =
0, die Bedingung:
Textabbildung Bd. 187, S. 107
zur Beurtheilung der Empfindlichkeit
erster Art oder der Empfindlichkeit für kleine Aenderungen der
Umdrehungsgeschwindigkeit ergibt.
Ist dann W' der Reibungswiderstand, welcher von dem Druck
des Gewichtes Q auf die Gelenkbolzen A und B herrührend auf die
Hülse D übertragen wird, so haben wir
Textabbildung Bd. 187, S. 107
oder mit Vernachlässigung der mit fρ und Δ₀φ multiplicirten Glieder einfacher
Textabbildung Bd. 187, S. 107
Ersetzen wir nun noch den Factor: aφ²/g durch μ sec ϑ₀, und führen den Werth von
M₀ in die Gleichung (18) ein, so gibt diese
für die relative Aenderung der Umdrehungsgeschwindigkeit oder für die Beurtheilung
der Empfindlichkeit erster Art den Ausdruck:
Textabbildung Bd. 187, S. 107
welcher mit dem für den einfachen Regulator gefundenen (15)
verglichen, zeigt, daß die Empfindlichkeit des Geiger'schen Regulators bei sonst gleichen Maaßen der Arme und Stelzen u.s.f.
fühlbar kleiner seyn muß als die des einfachen, da der Zähler des ersten Gliedes der rechten Seite (19) um
W'b größer ist als β, und das zweite den Factor μ
enthält, welcher nach der Bedingung (4) auch durch den Ausdruck:
Textabbildung Bd. 187, S. 108
dargestellt wird, der also für positive x' immer größer als 1 ist.
Der Widerstand W' besteht aus drei verschiedenen
Reibungswiderständen, aus der Zapfen-Reibung in A, aus der gleitenden Reibung des Bolzens B längs
ab, und aus der drehenden Reibung dieses
Bolzens auf ab; ist also N der Druck in B auf ab, N₁ der Druck in A, ρ₂ der Halbmesser der Gelenkbolzen A und B, so hat man für das
Moment in Bezug auf A der ersten Reibung: fρ₂N₁,
für das der gleitenden Reibung auf ab: f₁Nl sin ζ, und für das der drehenden Reibung auf
ab in Bezug auf die Achse von B; fρ₂N. Die
Summe dieser Momente gibt das Moment W'l cos ζ
des auf die Hülse übertragenen Widerstandes, und man hat demnach
Textabbildung Bd. 187, S. 108
worin die Summe N + N₁ als eine absolute, d.h. ohne Rücksicht auf die
Zeichen von N und N'
aufzufassen ist.
Was nun die Empfindlichkeit zweiter Art betrifft, so geht
aus der Untersuchung des vorhergehenden § hervor, daß es dazu genügt, die
Beziehungen zwischen den Winkelbeschleunigungen: dψ/dt und dψ'/dt und der
Beschleunigung der Hülse: dw/dt für den Anfang der Zeit
t auszudrücken. Dazu ergibt sich aus der Gleichung:
z = 2 b (cos ϑ₀ – cos
ϑ) wie oben
Textabbildung Bd. 187, S. 108
und für
Textabbildung Bd. 187, S. 108
ferner genügt es für unseren Zweck die Coordinaten von J in Bezug auf AB,
Fig. 3,
als constant anzunehmen, und demgemäß ψ' = dζ/dt zu setzen, so daß aus der Gleichung: z = l sin ζ
einfach
Textabbildung Bd. 187, S. 108
folgt. Damit gibt dann die Gleichung (17) zur Beurtheilung der
Empfindlichkeit zweiter Art das Verhältniß:
Textabbildung Bd. 187, S. 109
dessen rechte Seite noch mit den Werthen von gM und gM'o umzuformen wäre;
es genügt aber schon die vorhergehende Form, um zu sehen, daß auch bezüglich dieser
Empfindlichkeit der Geiger'sche Regulator dem einfachen
nachsteht, da der Nenner der rechten Seite durch das zweite Glied wesentlich
vergrößert erscheint.
VIII.
Werfen wir nun zur Anwendung des Vorhergehenden die Frage auf: Wie muß der Geiger'sche Regulator eingerichtet werden, damit er für
sonst gleiche Verhältnisse die größte Empfindlichkeit erhält? so kann sich die
Beantwortung dieser Frage nur auf die zweckmäßigste Lage der Curve G'
FG, Fig. 3, oder des
Berührungspunktes F beziehen und für eine bestimmte
Stellung der Kugeln und des Hebels AB gelten. Dazu
bietet sich natürlich die normale Stellung der Kugeln und die horizontale Lage des
Hebels AB am nächsten dar, da man ohnehin darnach
streben muß, die Empfindlichkeit für diese normale Lage am größten zu machen,
wodurch übrigens die Berücksichtigung anderer Lager nicht ausgeschlossen ist.
Die allgemeine Antwort auf unsere Frage wird dann dahin gehen, daß diejenige Lage des
Punktes F die günstigste ist, für welche der Widerstand
W' und das Massemoment M'₀ die kleinsten Werthe erhalten und der Factor μ = 1 wird, und alle diese Bedingungen führen auf
die eine:
x₀ = 0,
wornach also der Punkt F mit dem
Punkt A zu vereinigen ist. Denn der Werth (20) von W' zeigt, daß für ζ =
0.
W' = fρ₂/l (N + N₁)
wird, und da man mit Vernachlässigung der Reibungswiderstände
bei der Bestimmung von N und N₁ setzen kann:
Q = N + N₁, für x₀ > 0, < l, und
Q = ± (N – N₁), für
x₀ > l, <
0,
und da man immer Nl = Qx₀ haben muß, so ergeben sich die
absoluten Summen: N + N₁ = Q, und N + N₁ = ± Q (2
x₀/l – 1).
Es hat demnach nur von x₀ = 0 bis x₀ = l Summe N + N₁ den kleinsten
Werth: Q; für x₀ = 0
aber wird N₁ = Q, N =
0, und damit fällt in dem Ausdruck (20) für W' das
Glied: f₁ N tang
ζ auch für ein von 0 verschiedenes ζ weg, und dieser Widerstand wird so für alle Lagen des Hebels der
möglich kleinste. – Der Werth von gM' kommt für
ζ = 0, x' = x₀ auf den einfachen:
gM' = Q (x₀² + 1/2
r₂²)
zurück, wenn r₂ der
Halbmesser des als Cylinder berechneten Läufers ist, und wird demnach auch für
x₀ = 0 am kleinsten, und daß der Werth von
Textabbildung Bd. 187, S. 110
mit x₀ = 0 der 1 gleich
wird, fällt unmittelbar in die Augen.
Für diese Annahme kann dann die 2. Gleichung (5) nicht mehr zur Bestimmung von Q dienen; dieses Gewicht bleibt mehr oder weniger
willkürlich, da es nur durch den Ausdruck (6) für den Parameter k der Curve G'FG, für unsere
jetzige Annahme:
Textabbildung Bd. 187, S. 110
nach welchem k und Q verkehrt proportional sind, in seiner Größe oder
vielmehr Kleinheit beschränkt wird; denn unsere Bedingungen für die Empfindlichkeit,
von denen die erste (19) nun die bestimmtere Form:
Textabbildung Bd. 187, S. 110
die zweite (21) die Form:
Textabbildung Bd. 187, S. 110
erhält, zeigen, daß die Empfindlichkeit in beiden Fällen um so
größer wird, je kleiner Q ist. Es darf aber auch k nicht zu groß werden, weil der Läufer Q dann zu große Wege zurückzulegen hat. Es dürften sich
daher für diese in Fig. 7 angedeutete zweckmäßigste Einrichtung des Geiger'schen Regulators die folgenden Maaße als die geeignetsten
empfehlen:
α = 45°,
b = l =
cos α = 1/2 √2, k = a√2,
Q = 1/2 P;
nimmt man dann noch ρ₂ = ρ, r₂ = 1/5 a, so erhält man die entsprechenden Werthe:
Textabbildung Bd. 187, S. 110
Dem letzteren Ausdruck ist keine absolute Bedeutung beizulegen, er kann nur zur
Vergleichung verschiedener Constructionen dienen; der erste Ausdruck dagegen gibt
die Grenze der Genauigkeit an, welche mit dem Regulator erreicht werden kann, und
dient auch umgekehrt dazu, das Verhältniß von W zu P zu berechnen, welches zur Erreichung einer gegebenen
Genauigkeit nothwendig ist. Soll z.B. unser Regulator, der vollkommen der Theorie
entsprechend construirt sey, nicht mehr als 1/2 Proc. = 1/200 von der normalen
Umdrehungsgeschwindigkeit abweichen, so muß in der normalen Lage die Abweichung noch
geringer, also etwa 1/250 seyn, und wenn man hat
γ = fρ/a = 1/500, so muß β = 1/250
– 1/400 = 3/2000 = 0,0015
werden; da nun nach den angenommenen Werthen
β = √2/4 W/P, so muß man P = 2000/3.
√2/4 W oder nahe = 236 W
nehmen, um die gewünschte Genauigkeit zu erreichen.
IX.
Die zuletzt besprochene zweckmäßigste Einrichtung des Geiger'schen Regulators führt auf eine naheliegende Abänderung desselben,
welche zwar vom theoretischen Standpunkte nicht als eine Verbesserung angegeben
werden kann, die aber wegen größerer Einfachheit in der Ausführung durch Beseitigung
des Läufers und seiner Bahn von dem praktischen Maschinenbauer als eine wesentliche
Verbesserung der Geiger'schen Construction aufgefaßt
werden mag. Nimmt man nämlich den Kreis G'AG
Fig. 7, vom
Halbmesser k mit dem Mittelpunkt O als Bahn des Läufers J, so wirkt das Gewicht
Q in allen Lagen des Hebels AB gerade so, als wenn es im Mittelpunkte O der Bahn befestigt wäre, da O und J immer in derselben Verticalen
liegen.Dieß gilt übrigens, wie Fig. 5 andeutet,
nicht nur für die obige besondere Lage der kreisförmigen Bahn, sondern für jede Lage derselben. Man kann daher das Gewicht Q in Kugelform
unmittelbar am Ende des zu AB senkrecht stehenden
Halbmessers AO = k
befestigen und so dem Regulator die durch Fig. 8 angedeutete
Construction geben, wobei es dann aber vortheilhafter seyn wird, k kleiner und Q größer zu
nehmen als oben angegeben wurde. Man könnte damit zugleich noch eine andere
Abänderung verbinden, welche zwar dem Praktiker weniger zusagen dürfte, die aber
eine noch größere Annäherung an die vollkommene Gleichung (7) gibt, als sie die
Construction Fig.
7 mit kreisförmiger Bahn besitzt, indem man nämlich statt der Verbindung Fig. 3 zwischen
AB und T die
Verbindung Fig.
5 mittelst Zahnstange und Bogen einführt.Die Verzahnung könnte übrigens auch zur Erzielung eines sanfteren Ganges
durch zwei, an den Endpunkten des Bogens CD
Fig. 5
und an der Stange T zu befestigende schwache
Uhrfedern ersetzt werden. Denn man hat dann die Beziehungen:
2b (cos
ϑ – cos α) = lζ, N
= Q (k sin ζ)/l,
und demnach für den Beharrungszustand die Bedingung:
P/2g
a²φ² l/b ζ – Q kb/l sin
ζ = 0,
oder mit Berücksichtigung des Werthes von k einfach:
ζ – sin
ζ = 0, (23a)
während die Verbindung Fig. 3 zwischen AB und T, wie leicht
zu sehen, auf die Bedingung:
sin ζ – tang ζ =
0 (23b)
führt, welche offenbar weniger genau ist als die erste, da die
Differenz: tang ζ – sin ζ über dreimal so groß ist als die Differenz: ζ – sin
ζ.
Beide Gleichungen (23) sind übrigens durch keinen Werth von ζ, außer ζ = 0 zu befriedigen,
und sie deuten dadurch an, daß strenggenommen nur bei der horizontalen Lage des
Hebels AB der Beharrungszustand mit der normalen
Umdrehungsgeschwindigkeit φ eintreten kann; es
wird daher nothwendig seyn, den bei diesen Constructionen vorkommenden größten
Fehler, d. i. den relativen Unterschiedet Δφ/φ zwischen der normalen Umdrehungsgeschwindigkeit
φ und derjenigen φ + Δφ, welche bei der
größten oder kleinsten Ausweichung ϑ₁ der
Kugeln oder der entsprechenden Neigung ζ₁
des Hebels den Beharrungszustand herstellt, durch Rechnung nachzuweisen.
Dazu hat man folgende den Gleichungen (4) und (5) entsprechende Beziehungen, und zwar
a) für die Verbindung Fig. 7:
P/g a² (φ + Δφ)²
cos ϑ – Pa – Q bk/l tang ζ = 0
P/g a²φ² cos α –
Pa = 0, 2b (cos ϑ
– cos α) = l sin ζ,
b) für die Construction Fig. 8:
P/g a² (φ + Δφ)²
cos ϑ – Pa – Q bk/l sin ζ = 0
P/g a²φ² cos ϑ –
Pa = 0, 2b (cos ϑ
– cos α) = lζ;
setzt man nun darin wieder φ² + 2φΔφ
für (φ + Δφ)², zieht die zusammengehörenden Gleichungen von
einander ab, und führt für cos ϑ den Werth in ζ ein, so ergeben sich folgende Werthe für die
größten relativen Abweichungen von der normalen Umdrehungsgeschwindigkeit, und zwar
im Falle a):
Textabbildung Bd. 187, S. 113
und im Falle b):
Textabbildung Bd. 187, S. 113
Man schließt daraus, daß die betreffenden Fehler nahezu den Differenzen ζ₁ – sin
ζ₁ und ζ₁ –
sin ζ₁ proportional sind; im Falle a) ist die Umdrehungsgeschwindigkeit für positive ζ zu groß, für negative zu klein, und das
Umgekehrte findet im Falle b) statt; in beiden Fällen
aber ist der Fehler für negative ζ größer als für
gleiche positive ζ. Wie klein übrigens diese
Fehler sind, geht augenfällig aus folgenden Zahlenwerthen hervor. Für l = b, α =
45°, ζ₁ = ± 8° findet
man:
ζ₁ =
+ 8°,– 8°,
a) Δφ/φ =
+ 0,000440,– 0,000536,
b)
Δφ/φ =
– 0,000146+ 0,000178
im Falle a) beträgt also die
größte Abweichung von der normalen Umdrehungsgeschwindigkeit nur etwas mehr als
1/2000 oder 1/20 Proc., und im Falle b) ist sie weniger
als ein Dritttheil davon; sie ist also in beiden Fällen kaum wahrnehmbar, und beide
Constructionen können selbst für noch größere Werthe von ζ₁, besonders mit Rücksicht auf die beschränkte
Empfindlichkeit erster Art, als vollkommen genaue Regulatoren bezeichnet werden.
Diese Empfindlichkeit erster Art, bezüglich der Ausdruck (22a) für dieselbe, bleibt nämlich der gleiche für
beide Constructionen, Fig. 7 und 8, und dürfte nach dem am
Ende des §. VIII berechneten Beispiel kaum auf 1/10 Proc. herabzubringen
seyn.
Bezüglich der Empfindlichkeit zweiter Art dagegen steht die Construction nach Fig. 8 ziemlich
im Nachtheil gegen die nach Fig. 7, da bei jener das
Massemoment gM' constant und
größer als Q/g k² = P/g .
P/4Q . l⁴/b⁴. a²/cos² α wird. Macht man daher
Q = P, k = 1/2 a√2 = b = l, so hat man
gM' = 1/2
Pa² und E₂
= 2/3 √2,
und dieser Werth verhält sich zu dem in VIII gefundenen: E₂ = √2 (1 – 0,0002) nahe wie 2 :
3. Gegen die praktischen Vortheile der Einrichtung
Fig. 8 dürfte
indessen dieser Nachtheil nur wenig in Anschlag zu bringen seyn.
X.
Nun besteht aber noch zwischen den Voraussetzungen für die Theorie des Geiger'schen Regulators und der gewöhnlichen, auch in
Fig. 12
dargestellten Ausführung ein wesentlicher Unterschied; bei jener Theorie wurde
nämlich angenommen, daß die horizontalen Drehungsachsen für die Kugeln in der
verticalen Drehungsachse zusammenfallen, während sie in der Ausführung zu beiden
Seiten dieser Achse liegen. Um den daraus entspringenden Fehler zu ermitteln, sey
CC
'
Fig. 9, und
ebenso, damit das Knie C'
ED
' ein gleichschenkliges bleibt, auch DD
' = n, und n/a = v; dann ist der
Centrifugaldruck einer Kugel in der normalen Stellung = P/g
aφ² (v + sin α) und sein Moment in Bezug auf C'
wird: P/g a²φ² (v + sin
α) cos α, und da alles Uebrige
unverändert bleibt, so hat man mit Beibehaltung der Verbindung und Einrichtung Fig. 7, und l = b gesetzt, für den
Beharrungszustand bei horizontaler Stellung des Hebels AB die Bedingungsgleichung:
P/g a²φ² (v + sin α) cos α – Pa sin α = 0,
für irgend eine andere Stellung wird die
Umdrehungsgeschwindigkeit wieder = φ + Δφ werden müssen, und die Gleichung für
den Beharrungszustand die aus den früheren abgeleitete Form:
P/g a² (φ + Δφ)² (v + sin ϑ) cos ϑ – Pa sin
ϑ – Qk tang ζ sin ϑ
= 0
annehmen. Zieht man die erste Gleichung von dieser letzten ab,
nachdem das Glied mit v ausgeschieden und für (φ + Δφ)² der frühere angenäherte Werth gesetzt worden, so
folgt die Bedingung:
P/g a²φ² (cot ϑ
– cot α) + 2 P/g a²φ² (v cot ϑ + cos ϑ) Δφ/φ
+ P/g a²φ² (cos ϑ
– cos α) – Qk tang ζ = 0
oder mit den früheren Werthen von cos
ϑ – cos α und k einfacher
4 (v cot ϑ + cos ϑ) Δφ/φ + 2v (cot ϑ – cot
α) + sin ζ – tang ζ = 0. (25)
Vernachlässigt man dann noch die kleine Differenz: tang
ζ – sin ζ, so kann man
daraus den Ausdruck für den größten relativen Fehler in der Umdrehungsgeschwindigkeit in
der nachstehenden einfachen Form ziehen:
Textabbildung Bd. 187, S. 115
worin ϑ₁ der größte
oder kleinste Werth von ϑ ist. Man findet z.B.
für α = 30°, ϑ₁ =20° und 40°, was einem ζ₁ = + 8° 30' und = – 11° 30' entspricht und
ν = 1/20 = 0,05, was ziemlich der kleinste in
der Anwendung vorkommende Werth seyn dürfte, die Abweichungen:
Δφ/φ = –
0,0236 und = + 0,0164,
oder im Mittel nahe 2 Proc.
Diese Abweichung mag für viele Fälle der Anwendung hinreichend klein erscheinen, um
unberücksichtigt bleiben zu können; aber im Hinblick auf die oben bewiesene viel
größere Genauigkeit der Regulatoren Fig. 7 und 8 und die möglicherweise
zu erreichende Empfindlichkeit derselben ist eine solche Abweichung doch kaum
zulässig, oder jede Theorie ist zwecklos. Diese Abweichung kann aber auch leicht
vermieden werden, wenn man, wie oben in §. VI schon vorgeschlagen wurde, die
oberen Enden der Arme C'K mit erweiterten Gabeln
versieht, diese die verticale Welle umspannen, und die vereinigten horizontalen
Achsen C' die geometrische Achse CD senkrecht schneiden läßt. Man erzielt dadurch
nicht nur eine vollständige Uebereinstimmung der Construction mit den Forderungen
einer Theorie, welche zu einfachen Ergebnissen führt, während eine solche mit
Zugrundelegung der Einrichtung Fig. 9 nicht durchgeführt
werden kann; man vermindert auch wesentlich die Reibung an den Gelenken C, und erspart endlich die Führung für die Arme CK, ohne daß durch das so häufig wechselnde
Bestreben der Kugeln, bald der Umdrehungswelle vorzueilen bei verminderter
Umdrehungsgeschwindigkeit, bald zurückzubleiben bei eintretender Beschleunigung
derselben, die Gelenke C wackelig werden.
Endlich kann man diesen ganzen Regulirungs-Apparat noch dadurch vereinfachen,
daß man an dem Hebel AB selbst das Gestänge zur
Uebertragung der Bewegung der Hülse auf die Dampfklappe einhängt, wodurch ein Hebel
und zwei Gelenke erspart werden und man erhält so die in Fig. 13 dargestellte
einfachste und mit der Theorie vollkommen übereinstimmende Einrichtung des Geiger'schen Regulators. An der Welle M sind in entsprechenden Entfernungen die Hebel L, N und K befestigt; der
erstere ist wie ursprünglich und in Deutschland meistens gebräuchlich, mit einer
Gabel versehen, welche in die mit einer Nuth versehene Hülse D eingreift, und besitzt demnach die unserer Theorie in Fig. 3 zu Grunde gelegte
Verbindung mit dieser Hülse; der senkrecht zu L stehende
Hebel N
trägt am oberen Ende
die Kugel Q, deren Gewicht dem Gewichte einer
Schwungkugel K gleich ist, weßhalb denn auch alle
anderen am Ende des §. IX angegebenen Gleichheiten, nämlich CE = ED = L = N, oder b = l = k = 1/2 a√2 für α = 45°, beobachtet sind. Der Hebel R dient zur Verbindung mit der Dampfklappe.
XI.
Einfacher noch als der in Fig. 13 dargestellte
Regulator, weil des Hülfsgewichtes Q entbehrend, aber
auch weniger genau, ist die im polytechnischen Journal, 1855, Bd. CXXXVIII S. 321
aus Wien mitgetheilte „Vereinfachung des Franke'schen parabolischen
Centrifugal-Regulators.“ Das Princip desselben besteht darin,
daß der Parabelbogen, auf welchem sich der Mittelpunkt der Schwungkugel bewegen
sollte, durch einen Kreisbogen ersetzt wird, der durch die Mitte und die beiden
Endpunkte jenes parabolischen Bogens geht, und nach der bekannten Construction eines
durch drei Punkte zu ziehenden Kreises bestimmt werden soll.
Was nun zunächst das Princip betrifft, so ist dieses darin mangelhaft, daß zwar der
betreffende Kreisbogen dem idealen Parabelbogen sehr nahe kommt, daß aber der
Halbmesser des ersteren, welcher die Richtung des von dem festen Mittelpunkte
ausgeübten Widerstandes angibt, nicht auch in allen Punkten mit der Normalen zur
Parabel, d. i. mit der Richtung der Resultirenden N
Fig. 2 aus dem
Gewicht und dem Bewegungsdruck einer Schwungkugel zusammenfallen kann, wie es für
den Beharrungszustand erfordert wird. Diese Bedingung wird bei jener Construction
nicht einmal für die Mitte des Bogens, welcher die normale Lage seyn soll, erfüllt,
es muß daher sowohl für diese Lage als für die beiden Endpunkte die
Umdrehungsgeschwindigkeit von der als normal angenommenen mehr oder weniger
abweichen.
Bezeichnet man den Parameter der Parabel mit p und
berechnet man den Halbmesser r und die Coordinaten a und b des Mittelpunktes
für den Kreisbogen durch drei Punkte der Parabel, deren Coordinaten in Bezug auf
Achse und Scheitel sind:
y₁ = 1/2 p,x₁ = 1/8 p,
y₀ = 3/4 p,x₀ = 9/32 p,
y₂ = p,x₂ = 1/2 p,
so findet man:Die nicht sehr einfachen Formeln zu dieser Berechnung finden sich in jedem
Lehrbuche der analytischen Geometrie.
a = 119/64p = 1,8594p, b = –
105/256p = – 0,4102p,
r = 1,9587p,
wobei das – Zeichen vor dem Werthe von b andeutet, daß der Mittelpunkt der betreffenden
Kreisbogen je auf der entgegengesetzten Seite der verticalen Drehungsachse liegt. Es
ist aber einfacher das b absolut zu nehmen, so daß y + b die Ordinate und
Textabbildung Bd. 187, S. 117
die Abscisse eines Kreisbogen-Punktes in Bezug auf ein
durch den Mittelpunkt dieses Bogens gelegtes zur Parabelachse paralleles
Coordinatensystem ausdrückt. Damit wird dann die Gleichung für den Beharrungszustand
bei der Umdrehungsgeschwindigkeit φ zuerst
Textabbildung Bd. 187, S. 117
und dann mit der Beziehung: g =
pφ² einfacher:
x'y – p (b + y) =
0, (27)
und man wird sich leicht überzeugen, daß zwar für die drei
Punkte, welche in der Parabel selbst liegen, x' auch a – x wird, daß aber
die Gleichung (27) durch keines der obigen Paare zusammengehöriger Werthe von x und y, also für keinen der
drei Punkte der Parabel, durch welche der Kreisbogen gezogen wurde, befriedigt wird.
Setzen wir daher zur Berechnung der Abweichungen von der normalen Geschwindigkeit
φ in der Gleichung (27) wieder φ² (1 + 2 Δφ/φ) statt φ² oder nun 1/p (1 + 2 Δφ/φ) statt 1/p, so finden wir allgemein:
Textabbildung Bd. 187, S. 117
und darnach ergeben sich für die genannten drei Punkte die
Werthe:
Δφ/φ = + 11/444, = – 6/606,
= + 13/696,
= +
0,0248, = – 0,0099, = + 0,0187;
für die als normale Lage angenommene Mitte des Bogens beträgt
demnach die Abweichung 1 Proc., für die Endpunkte desselben nahe 2 und 2 1/2 Proc.,
und es wird also die Genauigkeit dieses Regulators von der möglichen Empfindlichkeit
desselben, die von der des einfachen Regulators wenig verschieden ist, weit
übertroffen, und es dürfte zweifelhaft seyn, ob derselbe für Spinnereien und
Webereien den Anforderungen an einen solchen Apparat genügt.Es scheint wenigstens die rasche Verbreitung des Geiger'schen und des complicirten Farcot'schen Regulators dafür zu sprechen, daß man in vielen
Etablissements das Bedürfniß eines genaueren Regulators
fühlt. Der in dem belgischen Bericht über die Pariser
Industrie-Ausstellung beschriebene und abgebildete Farcot'sche Regulator beruht zunächst auf
demselben Princip wie der obige vereinfachte Franke'sche, er unterscheidet sich aber von diesem einmal dadurch,
daß bei ihm nicht bloß die Kugelträger, sondern auch die die Hülse
schiebenden Stelzen gekreuzt, und an dieser so befestigt sind, daß sie mit
den Kugelträgern immer ein gleichschenkeliges Knie bilden, dann aber
hauptsächlich dadurch, daß derselbe mit einer weiteren Correction für die
aus dieser Construction sich ergebenden Abweichungen versehen ist. Dieser
Correctionsapparat besteht aus einer Spiralfeder und einem Gegengewicht, von
denen die erste die Hülse abwärts drückt, und der Beschreibung zufolge dem
Bewegungsdruck der betreffs ihrer wirksamen Masse veränderlichen Kugelträger
entgegen wirken soll, während das Gegengewicht durch einen zweckmäßig
gekrümmten Hebel, auf welchen sich die zur Dampfklappe niedergehende und
verlängerte verticale Stange des Steuerungsapparates mittelst einer Rolle
stützt, die anderen Fehler des Apparates zu beseitigen bestimmt ist. Es ist
daher sowohl die Construction als die Theorie des Farcot'schen Regulators eine ziemlich complicirte (weßhalb der
ersteren auch viel Empirie zu Grunde liegt), und der Geiger'sche Regulator nach der in Fig. 13
dargestellten Construction ist ihm gewiß in jeder Hinsicht vorzuziehen, eine
weiter eingehende Untersuchung desselben also überflüssig.
Uebrigens kann dieser Regulator für solche Fälle, in dienen seine Genauigkeit genügt,
bezüglich seiner Construction mehrfach verbessert werden. Denn beachtet man, wie
schwierig es ist Mittelpunkt und Halbmesser eines Kreisbogens, der durch drei im
Vergleich zur Länge des Halbmessers sehr nahe liegende Punkte gezogen werden soll,
genau zu construiren, so wird man zugeben müssen, daß zur Vermeidung noch größerer
Fehler jene Stücke strenggenommen, wie oben geschehen, berechnet werden müßten; diese etwas umständliche Berechnung kann man sich
aber ersparen, wenn man statt des vorgeschlagenen Kreisbogens durch drei Punkte der
Parabel pq
Fig. 10 den
Krümmungskreis mn derselben für die normale Lage
nimmt; denn die Bestimmungsstücke für diesen sind durch die einfachen Formeln:
Textabbildung Bd. 187, S. 118
gegeben, wenn y₀ die
Ordinate des betreffenden Parabelpunktes, und a und b die Coordinaten des Krümmungs-Mittelpunktes auf
Achse und Scheitel der Parabel bezogen, bezeichnen. Man findet darnach für den
Punkt: y₀ = 3/4 p der
Parabel die Werthe:
a = 59/32p = 1,844p, b = –
0,422p, r = 125/164 p = – 1,953p,
welche von den oben berechneten für den Kreis durch drei
Punkte so wenig verschieden sind, daß auch die allersorgfältigste Construction kaum
im Stande ist, solche und noch größere Abweichungen von den richtigen Werthen für
den letzteren Kreis zu vermeiden. Demungeachtet werden nun die Abweichungen von der
normalen Umdrehungsgeschwindigkeit fühlbar andere; denn man findet nun durch die Gleichung
(28) mit
Textabbildung Bd. 187, S. 119
folgende zusammengehörende Werthe:
y = 1/2 p,
= 3/4 p,
= p,
x' = 1,7219
p,
= 25/16 p,
= 1,3390 p,
Δφ/φ = + 0,0354,
= 0,
= + 0,03095
der Fehler in der Umdrehungsgeschwindigkeit wird demnach für
die beiden äußersten Lagen der Schwungkugeln etwas größer als oben, da er sich auf 3
und 3 1/2 Proc. erhöht, dafür aber ist er in der Nähe der normalen Lage, und in
dieser Nähe werden sich die Kugeln doch am meisten bewegen, kleiner, da er für diese
Lage selbst Null wird. Aus diesen Beispielen wird man erkennen, wie viel es auf die
genaue Ausführung der Construction des Kreises durch drei Punkte der Parabel ankäme.
Uebrigens zeigt die Gleichung (28), daß der relative Fehler der Ordinate y verkehrt proportional ist, daß derselbe also für die
ganze Bewegung der Hülse um so kleiner wird, je größer man das y₀ für die normale Lage nimmt, womit aber
freilich auch b und r rasch
wachsen.
Was dann die weitere Ausführung betrifft, so läßt sich die vorgeschlagene
„Vereinfachung des Franke'schen
Regulators“ noch wesentlich mehr vereinfachen, wenn man, wie es in
Fig. 10
angedeutet ist, die Arme CMK, welche die
Schwungkugeln tragen, zu beiden Seiten der verticalen Welle vorbeigehen läßt, sie in
solcher Weise krümmt, daß der Theil C, M derselben für
die normale Lage der Hülse D horizontal gerichtet ist,
und darin der verticalen Achse gegenüber einen cylindrischen Bolzen B befestigt, welcher in eine entsprechende horizontale
Nuth der Hülse D eingreift, so daß die Arme CMK selbst ohne das bei der Vereinfachung des Franke'schen Regulators (auch bei dem Farcot'schen Regulator) beibehaltene Knie die Hülse D durch den Bolzen B heben
und niederdrücken. Der Doppelarm CAC', welcher die
Gelenke für die Arme CMK enthält, kann dann, wenn
man nicht die oben besprochene bessere Einrichtung vorzieht, zugleich zur Führung
dieser Arme eingerichtet werden, so daß der Arm für die Kugel rechts am rechten Arm
AC gleitet, der für die Kugel links am linken
Arm. Durch diese Einrichtung erspart man nicht nur die Kniestelzen mit ihren
Gelenken, sie besitzt auch den Vorzug, daß die Verschiebungen der Hülse für gleiche
Ausweichungen der Schwungkugeln aus der normalen Lage nahe gleich werden, und diese
letztere Lage demnach auch die mittlere Lage ist, und daß
der Widerstand gegen die Bewegung der Hülse immer nahe senkrecht zu den Hebelarmen
bleibt, welche die Hülse bewegen.
Für diese Einrichtung sind dann auch die Bedingungen für die Empfindlichkeit leicht
herzustellen, was ich indessen dem sich dafür interessirenden Leser überlassen
will.
XII.
Allen Anforderungen an einen guten Regulator genügt in der einfachsten Weise der rein
parabolische Centrifugal-Regulator, wenn ihm die in den Fig. 14 und 15
dargestellte Einrichtung gegeben wird, bei welcher er die größtmögliche Genauigkeit
mit der größten Einfachheit und Empfindlichkeit verbindet. Die gewöhnlichen
Schwungkugeln sind hier in schwere massive cylindrische Läufer L umgewandelt, welche mit ihren gewölbten Mantelflächen
zwischen abgerundeten Ansätzen auf der festen cylindrischen Bahn BAB rollen und von dieser selbst den nöthigen
Druck zur Beschleunigung oder Verzögerung ihrer rotirenden Bewegung um die verticale
Achse AA erhalten. Bei der rollenden Bewegung auf
BAB drehen sich diese Läufer um die in die
gabelförmigen Enden der Stelzen G eingeschraubten
Spitzen J, welche in ihren horizontalen geometrischen
Achsen ii eindringen, und die Bahn BAB ist so gekrümmt, daß sich diese Achsen in der
durch Gleichung (2) ausgedrückten Parabel bab
bewegen. Die Stelzen G sind an ihren oberen Enden E mit den an der beweglichen Hülse S befestigten Armen F, deren
Länge so bemessen ist, daß jene Stelzen für die normale oder mittlere Lage der
Läufer L vertical stehen, durch Gelenke verbunden.
Endlich ist an der Welle AA auf die Länge des
Weges der Hülse S eine Rippe oder Feder M angebracht, um etwaigen Drehungen dieser Hülse in
Folge der Reibung, welche durch die in ihre kreisförmige Nuth eingreifende Gabel
erzeugt wird, vorzubeugen.
Die in die Augen springenden Vorzüge dieser Einrichtung sind folgende:
1) der Apparat ist sehr einfach; es sind auf jeder Seite der verticalen Welle AA nur zwei Drehungspunkte E und J vorhanden;
2) diese Drehungspunkte haben nur einen geringen Druck zu erleiden; denn die Normalen
zur Bahn AB sind auch normal zur Parabel ab, diese Bahn AB hält also in jeder Lage des Läufers L durch
ihren Widerstand der Resultirenden aus dem Gewicht und Bewegungsdruck eines Läufers
das Gleichgewicht, und die Drehungspunkte J und E haben daher nur den Druck zu erleiden, welcher aus dem
Widerstand gegen die Bewegung der Hülse entspringt, während bei allen anderen
Regulatoren jener ganze Druck auf den Gelenken, um welche sich die Kugeln bei ihrer
steigenden oder sinkenden Bewegung drehen müssen, oder wie bei dem Franke'schen Regulator auf den Zapfen der Rollen, welche
die parabolische
Bewegung der Kugeln vermitteln, lastet und in Folge dessen auch eine entsprechend
große Reibung erzeugt;
3) aus diesem Grunde können denn auch die Arme F, die
Stelzen G, die Gelenkbolzen E und die Spitzen J ziemlich schwach seyn; nur
die Bahn AB erfordert eine jenem Druck
entsprechende Stärke und Steifigkeit, und während
4) bei allen sonstigen Regulatoren das Moment der Reibung an jenen Gelenken mit der
Vergrößerung des Gewichtes der Schwungkugeln wächst, und zwar in einem größeren
Verhältniß als dieses, weil auch die Gelenkbolzen stärker werden müssen, und
demzufolge die Empfindlichkeit des Regulators durch das Glied γ in der Gleichung (15) beschränkt wird, ist diese bei unserem
Regulator von jenem Gewicht ganz unabhängig, da zwischen dem Läufer, dessen
Wälzungskreis einen ziemlich großen Durchmesser erhalten kann, und seiner Bahn nur
rollende Reibung stattfindet, welche bei gehöriger Reinhaltung der letzteren
verschwindend klein ist.
5) Die Hebung und Senkung der Hülse S erfolgt unmittelbar
durch die schweren Massen L und hält nahe gleichen
Schritt mit der verticalen Hebung und Senkung der Achsen J derselben; die Hebung der Hülse ist etwas kleiner als die der Achse J, die Senkung etwas größer, und da die Parabel aufwärts
stärker steigt, als sie abwärts fällt, so erhält die Hülse für gleiche Wege der
Achse J zu beiden Seiten der normalen Lage auch nahe
gleich große Verschiebungen.
Die Genauigkeit unseres Regulators ist nur durch die mechanische Ausführung des
Bogens AB beschränkt, die zwar nicht so leicht
ist, als die Herstellung eines cylindrischen Gelenkbogens, wogegen dieser Bogen aber
auch, einmal richtig hergestellt, seine Form nicht so leicht ändert, als jener
Bolzen, der sich, während der Regulator im Gange ist, fortwährend einseitig abnutzt.
Die Herstellung des Bogens AB kann übrigens mit
großer Genauigkeit ausgeführt werden, wenn man, wie in Fig. 16 angedeutet ist,
die Evolute MN der Parabel abc zu Hülfe nimmt, für welche die nothwendigen
Maaße in der Figur eingeschrieben sind, und zwar in der Art, daß man nach dieser
Evolute MN einen Cylinder von hartem Holz
möglichst genau herstellt, an der Mantelfläche desselben in N eine gerad ausgestreckte breite aber dünne Uhrfeder, und an dieser in
der entsprechenden Entfernung NC = NMA einen Reißerstift befestigt; bringt man dann
diesen Apparat über dem Metallbogen an, der für den Bogen AB bestimmt ist, so wird die Spitze des Reißers
bei gleichmäßiger Spannung der Feder die Curve ABC
auf jenen Metallbogen viel genauer und mit größerer Stetigkeit aufreißen, als es auf
andere Weise zu erreichen ist, weil der Einfluß kleiner Fehler im Bogen MN für die Beschreibung der Curve ABC ein verschwindend kleiner ist. Es dürfte dann
aber nicht überflüssig seyn, nach erfolgter Ausarbeitung des Metallbogens nach jenem
Risse denselben Apparat auch zum feinen Ausschlichten zu verwenden, indem man statt
des Reißerstiftes nun eine cylindrische Schlichtfeile befestigt und mit dieser der
Cylinderfläche ABC die letzte Vollendung gibt.
Wollte man übrigens hier betreffs der Genauigkeit recht bedenklich seyn und auch den
Einfluß des Gewichtes und des Bewegungsdruckes der Stelzen G beachtet sehen (das Gewicht der Hülse S und
ihrer Arme F wird immer als mit dem Steuerungsapparat
in's Gleichgewicht gebracht angenommen werden dürfen), so bezeichne man die Länge
EJ dieser Stelzen mit l, die Entfernung ihres Schwerpunktes von E
mit l', ihr Gewicht mit q,
und die Länge der Arme F von der Achse AA an mit b, so hat
man für den Bewegungsdruck einer Stelze auf die entsprechende Achse J den Ausdruck:
Textabbildung Bd. 187, S. 122
das Gewicht der Stelze dagegen fügt sich einfach dem des
Läufers hinzu und die Gleichung für den Beharrungszustand oder die
Differentialgleichung der Curve, für welche der Beharrungszustand überall mit der
Umdrehungsgeschwindigkeit φ stattfindet, wird
nun
Textabbildung Bd. 187, S. 122
die Gleichung der Curve selbst ist demnach
Textabbildung Bd. 187, S. 122
also immer noch eine Parabel, deren Parameter p' zu dem Parameter p der
Parabel (3) im Verhältniß von l² (P + q): Pl² + ql'²
steht und sonach etwas größer ist als p, deren Achse
aber nicht mehr mit der verticalen Umdrehungsachse zusammenfällt, sondern derselben
parallel zur Seite liegt, in einem Abstande:
Textabbildung Bd. 187, S. 122
Es bietet daher auch die Ausführung dieser vollkommen strengen Theorie, bei welcher
nun nichts mehr unberücksichtigt geblieben ist, was auf den Beharrungszustand
Einfluß hat, nicht mehr Schwierigkeit als die der einfachen, für welche q = 0 oder l' = l angenommen wurde, und die auf die Gleichung (3)
geführt hat.
Zum Schlusse erübrigt noch, die Bedingungen für die Empfindlichkeit unseres
Regulators abzuleiten, wobei es genügt, die einfache Parabel zu Grunde zu legen.
Sey ER
Fig. 11 die
Größe des halben Widerstandes 1/2 W gegen die Bewegung
der Hülse, ER' = JR' die
entsprechende Seitenkraft in der Richtung der um den Winkel ϑ aus der verticalen Lage gedrehten Stelze EJ, JR'' und JN die nach der Tangente und
Normale zur Parabel in J gerichteten Seitenkräfte der
nach J übertragenen Kraft JR', so hat man zunächst
Textabbildung Bd. 187, S. 123
Ist dann wieder P das Gewicht eines Läufers, φ + Δt
φ die Umdrehungsgeschwindigkeit des Regulators
während der steigenden Bewegung der Läufer, und beachtet man, daß der Widerstand
gegen diese Bewegung der Läufer selbst verschwindend klein ist, so hat man als die
in der Richtung der Tangente auf den Läufer J wirkende
Kraft:
Textabbildung Bd. 187, S. 123
und mit Einführung des angenäherten Werthes = φ² (1 + 2 Δtφ/φ) statt (φ + Δtφ)², dann mit Beachtung der Bedingung für
den Beharrungszustand:
Textabbildung Bd. 187, S. 123
wird jene Tangentialkraft
Textabbildung Bd. 187, S. 123
Die Kraft, welche den Läufer an der Achse J in Bewegung
setzt, hat aber nicht bloß die Masse P/g desselben zu
beschleunigen, sondern, weil dabei der Läufer sich um die horizontale Tangente an
der gewölbten Mantelfläche dreht, die Masse 3/2 P/g;
wenn daher v die Geschwindigkeit der Achse J ist, so wird die Bewegungsgleichung derselben
Textabbildung Bd. 187, S. 123
Für den Anfang der Zeit t oder den Anfang der steigenden
Bewegung von einem Beharrungszustande an, für welchen die Winkel ϑ₀ und τ₀ gelten, zieht man daraus die Bedingung:
Textabbildung Bd. 187, S. 123
welche mit den Beziehungen: tang
τ₀ = p/y₀ = p/(b + l sin ϑ₀) auch die Form:
Textabbildung Bd. 187, S. 124
und für die unserer Construction Fig. 14 zu Grunde
liegenden Maaße: b = p, l =
2p, die besondere:
Textabbildung Bd. 187, S. 124
annimmt, und so zeigt, daß die Empfindlichkeit erster Art unseres Regulators durch Verminderung des
Bruches: W/4P beliebig groß
werden kann, und daß sie bei den gewöhnlichen Verhältnissen, wo l sin ϑ₀ immer kleiner als b seyn wird, für positive ϑ₀ etwas größer, für negative ϑ₀ etwas kleiner ist, als für die normale Lage ϑ₀ = 0.
Für diese Lage hat man einfach
E₁ = W/4P,
und schließt aus der Vergleichung dieses Werthes mit dem
Ausdruck (15) für den einfachen Regulator, daß, abgesehen von dem Gliede γ, für gleiche Werthe W und P in dem Werthe (14) von β das α = 2b werden müßte, wenn die Empfindlichkeit E₁ jenes Regulators der unseres parabolischen
nahe kommen sollte.
Bezüglich der Empfindlichkeit zweiter Art dagegen steht der letztere dem ersten etwas
nach. Man schließt aus Fig. 11
ζ = EE₀ = x – x₀ – l (l – cos ϑ),
y = b + l sin ϑ
und daraus folgen die Ableitungen:
Textabbildung Bd. 187, S. 124
womit aus der Gleichung (30) das Verhältniß folgt:
Textabbildung Bd. 187, S. 124
Für die normale Lage ist ϑ₀ = 0 und daher einfach
E² = 4/3 cos²τ₀;
dieses E₂ ist daher für die
zulässigen Verhältnisse, bei denen cos²τ₀ nicht viel größer als 1/2 seyn kann,
nahe = 2/3 während der Ausdruck (16) für E₂ des
einfachen Regulators mit α = 2b und sin²
ϑ₀ = 1/2 den Werth: 1 erhält.
Tafeln