| Titel: | Ueber die Betriebskraft der Remscheider Hammerwerke; von Robert Röntgen. |
| Autor: | Robert Röntgen |
| Fundstelle: | Band 189, Jahrgang 1868, Nr. XL., S. 185 |
| Download: | XML |
XL.
Ueber die Betriebskraft der Remscheider
Hammerwerke; von Robert
Röntgen.
Mit Abbildungen auf Tab.
III.
Röntgen, über die Betriebskraft der Remscheider
Hammerwerke.
Die in der Gemeinde Remscheid (preußische Rheinprovinz) befindlichen Hammerwerke
zerfallen in drei Classen, nämlich in Stahlraffinir- oder Reckhämmer, in Sägen- und in Sensenbreithämmer. Die ersteren dienen besonders zum Raffiniren und
Ausrecken des Stahles (des Roh-, Puddel- und Cementstahles), welcher
in den Kleinschmiedereien von Remscheid und Umgegend zur Fabrication der
verschiedenartigsten Stahlwaaren verwendet wird; die anderen werden zur Verfertigung
der Sägen- und Sensenblätter benutzt.
Diese sämmtlichen Hammerwerke, mehr denn hundert an der Zahl, sind fast von gleicher
Einrichtung; sie unterscheiden sich nur durch das Gewicht der eigentlichen Hämmer
oder der Hammerköpfe, durch die Länge der Helme oder Hammerstiele und durch die Zahl
der Schläge, die sie in einer gewissen Zeit machen.
Die Stahlraffinir- oder Reckhämmer besitzen durchschnittlich ein Gewicht von
50 bis 70 Pfd. (obgleich man seit einiger Zeit auch hier und da Hämmer von 90 und
mehr Pfund anwendet), einen Helm von 6¼ bis 6½ Fuß Länge, einen Hub
von 6 bis 8 Zoll und machen pro Minute 340 bis 400
Schläge. Das Gewicht der Sägenbreithämmer beträgt 90 bis 100 Pfd., die Länge ihres
Helmes beläuft sich auf 6 bis 6¼ Fuß (er ist also etwas kürzer als bei den
Stahlraffinirhämmern), ihr Hub beträgt 4 bis 4½ Zoll; sie machen in der
Minute 420 bis 460 Schläge. Von allen Hämmern laufen sie am schnellsten und werden
darin nur von den sogenannten Klipperhämmern, die wir
oben nicht angeführt haben und deren in der ganzen Gemeinde gegenwärtig nur zwei
oder drei vorhanden sind, übertroffen. Diese Hämmer von 30 bis 40 Pfd. Gewicht
werden in der Sensenfabrication benutzt und machen pro
Minute über 500 Schläge, so daß man die einzelnen Schläge kaum noch von einander
unterscheiden kann. In der Regel liegen 2 bis 3 solcher Hämmer vor einer Achse, die
alle gleichzeitig in Thätigkeit gesetzt werden können. Die Sensenbreithämmer endlich haben ein
Gewicht von 90 bis 95 Pfd., einen Hub von 5 Zoll; die Länge ihres Helmes beträgt
6½ Fuß und die Zahl ihrer Schläge beläuft sich auf 210 bis 240 pro Minute.
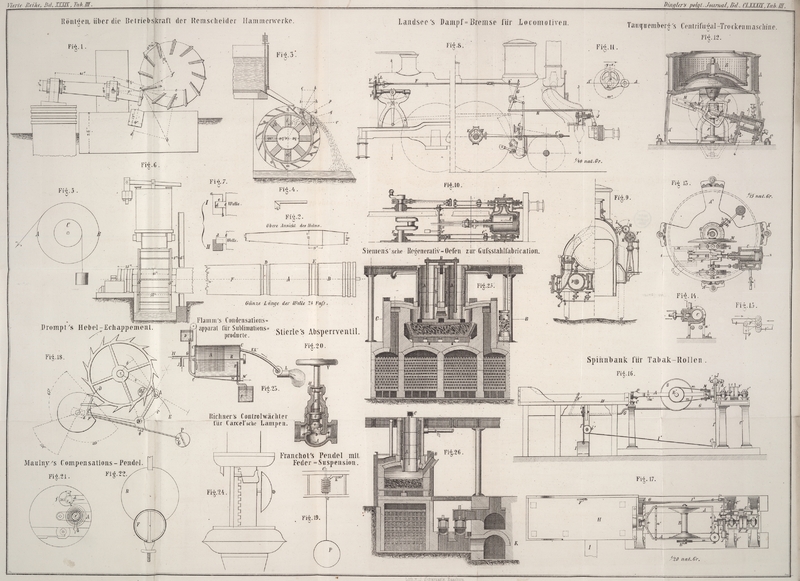
Die Helme besitzen die in Fig. 1 und 2 abgebildete Gestalt; sie
bestehen aus gesundem Buchenholze und wiegen im trockenen Zustande 140 bis 160 Pfd.
Die Hülse, vermittelst deren sich der Hammer in den Vertiefungen der sogenannten
Pfadeisen dreht, hat ein Gewicht von 220 bis 230 Pfd., und das hintere Helmband
wiegt 45 bis 50 Pfd. Es liegen nicht ganz ⅔ der Helmlänge vor der Hülse.
Das Helmband, welches unten mit einem kleinen Vorsprunge versehen ist, stößt mit
diesem auf den sogenannten Prallklotz oder Stößer. Die Entfernung vom vorderen Ende
der Amboßbahn bis zur Mitte des Prallklotzes beträgt 6 Fuß, wobei jenes Ende
6¼ bis 8 Zoll höher liegt als die Mitte des Prallklotzes. Der Amboß hat eine
Länge von 20 Zoll, während die Hammerbahn nur 5 Zoll lang ist, wodurch also die
Länge des sogenannten Geschläges, d. h. die Entfernung vom Helmbande bis zur Mitte
des Hammerkopfes verändert werden kann.
Die Daumenwellen, durch welche die Hämmer betrieben werden, bestehen aus Eichenholz.
Sie haben am dicksten Ende einen Durchmesser von 3½ bis 4 Fuß, am dünnsten
von 2¾ bis 3¼ Fuß; sie sind 20 bis 24 Fuß lang und ruhen vermittelst
gußeiserner Zapfen von 3½ bis 4¼ Zoll Durchmesser auf Lagern, die
meistens aus demselben Material bestehen. Leichtere Wellen werden auch wohl, um das
erforderliche Trägheitsmoment zu erhalten, mit gußeisernen Ringen von 1000 und mehr
Pfund umzogen.
An dem dünneren Ende der Welle ist das Wasserrad vermittelst 8 oder mehr Armen
befestigt, oder es ist, wie man dieß häufiger sieht, aufgekeilt (Fig. 3). Letztere Methode
der Befestigung ist natürlich nicht zu empfehlen. Die Räder besitzen
durchschnittlich einen Durchmesser von 8 Fuß; die lichte Weite beträgt 3 bis 5 Fuß.
Die Radkränze sind 10 bis 12 Zoll tief und aus 3- bis 5 zölligen eichenen
Bohlen zusammengesetzt. Den Radringen gibt man eine Dicke von 3 bis 4 Zoll. Alle uns
bekannten Räder enthalten 16 Schaufeln, welche 1½ Fuß lang und 1 bis
1½ Zoll dick sind. Der Radring sowohl wie die Radkränze sind behufs größerer
Festigkeit mit eisernen Ringen umzogen; auch sind die Enden der Wellen, sowie die
Daumenkränze mit solchen Ringen versehen.
Etwa 5 bis 6 Fuß vom dicksten Ende der Welle entfernt, sind die Daumen angebracht,
deren 12 in den dicksten und 10 in den dünnsten vorhanden sind. Ein solcher Daumen
ist in Fig. 4
abgebildet. Die
Entfernung der vorderen Daumenkanten in gerader Linie gemessen, beträgt bei den
dicksten Wellen für Reckhämmer circa 13 1/6 Zoll, für
Sensenbreithämmer 13½ Zoll. Bei dünneren Wellen ist diese Entfernung etwas
geringer, darf aber nicht unter 11½ Zoll heruntergehen, weil sonst die Daumen
beim vollen Gange den Hammer fangen. Der Weg des Leergehens ist demnach für dickere
Wellen etwas größer als für die dünneren. Die Daumen stehen 5/4 bis 1½ Zoll
aus der Welle hervor und besitzen mit ihrer Verkeilung auf dem Wellkranze eine Dicke
von 3 Zoll; ihre Breite beträgt 4½ Zoll. — Der Daumenstiel macht mit
dem Radius der Welle einen Winkel von 10 bis 15°, und die aufgreifende
Daumenfläche einen solchen von 40 bis 46°. Denkt man sich durch den
Angriffspunkt a eines Daumens (Fig. 1) eine Horizontale
hae gezogen, so geht diese durch den
Mittelpunkt der Hülse oder durch den Drehpunkt h des
Hammers. Nach meinen Vermessungen liegen nun bei den meisten Hammerwerken circa.¾ der Welle über dem angreifenden Daumen
oder über der Horizontalen he, so daß der Radius
für jenen Daumen, wie eine leichte Rechnung nachweist, eine Neigung von beinahe
30° nach abwärts besitzt. Bezeichnet nun a b =
v die Geschwindigkeit des Daumenkranzes, so zerlegt
sich diese in zwei andere, a d und a c, von welchen die erstere die Geschwindigkeit
bezeichnet, mit welcher das Schwanzende des Hammers niedergeworfen wird; die
letztere ist natürlich bestrebt, das Helmband abzuziehen. Nun ist ad = ab . cos bad = v . cos f a c = v . cos (f a e + e a c) = v . cos (f a e + a h g) = v . cos (α + β). Da α + β circa 44° beträgt, so hat man für die
Geschwindigkeit, mit welcher das Helmband niedergedrückt wird: v . cos 44° = 0,7193
. v. — Bei dem Sägenbreithammer ist α +
β etwas größer.
Ueber die Construction der Wassergerinne und deren Ausflußcoefficienten haben wir in
einem Aufsatze aus dem Jahre 1860, der in diesem Journale Bd. CLVIII S. 1
u. 81 erschienen ist, das Nöthige mitgetheilt.
Es soll nunmehr unsere Aufgabe seyn, die Betriebskraft der hiesigen Hammerwerke,
gestützt auf sorgfältige Vermessungen und Beobachtungen zu berechnen. Zwar sind
Versuche der Art schon im Jahre 1828 mit Hülfe des Dynamometers von Egen angestellt worden, die aber viel zu große Resultate
geliefert haben. Um jene Angaben und die unserigen mit einander vergleichen zu
können, theilen wir hier einen Auszug aus der Tabelle mit, welche Egen über seine Beobachtungen Zusammengestellt hat und
die in seinem Werke: „Untersuchungen über den Effect einiger im Rheinland
Westphalen bestehenden Wasserwerke“, S. 82, enthalten ist.
Textabbildung Bd. 189, S. 188
Nummer des Versuches;
Schützen-Oeffnung;, Druckhohe; Kraftmoment; Zeit eines Radumlaufes;
Effectmoment; Ganzer Widerstand; Breite; schräge Höhe
Wir haben schon in dem vorher angeführten Aufsatze nachgewiesen, daß Egen den Ausflußcoefficienten bei der Berechnung der
Wasserconsumtion um 18 Proc. zu klein angenommen und deßhalb den Nutzeffect des
Rades viel größer gefunden hat als er in Wirklichkeit ist. Vielfache Beobachtungen
haben uns aber auch gelehrt, daß die Räder oder Wellen der Hammerwerke bei den in
der Tabelle angegebenen Druckhöhen und Schützenöffnungen weit
mehr Umdrehungen in einer gewissen Zeit machen, als dort angegeben ist. So
beträgt nach unseren Beobachtungen — und Egen
bestätigt dieß in einer spateren Tabelle seines Werkes, die wir weiter unten
mittheilen werden — schon bei einer Schützenöffnung von ¾ Zoll Höhe
und 26 Zoll Breite die Zahl der Radumdrehungen pro
Minute 21 bis 22, vorausgesetzt, daß die Druckhöhe 4 bis 5 Fuß betrage, während nach
jenen Beobachtungen bei einer mehr als doppelt so großen Schützenöffnung (23,5
Linien Schützenhöhe) die Zahl der Umdrehungen nur 60/3,59 = 16 bis 17 betrug.
— Ebenso fanden wir für eine Höhe der Schützenöffnung von 5¼ Zoll und
bei der vorhin bemerkten Breite und Druckhöhe die Zahl der Radumdrehungen in der
Minute zu 38 bis 40, während sie nach der Tabelle nur 32 bis 33 beträgt. Die
Bremsung des Dynamometers ist also den Betriebsverhältnissen gar nicht angepaßt,
vielmehr in allen Fällen zu groß gewesen; die Versuche sind deßhalb auch vollständig
werthlos.
Auf die Unzuverlässigkeit dieser Versuche wurden wir besonders aufmerksam, als wir
nach einer Formel der Mechanik aus der Betriebskraft der Hammerwerke, der Zahl der
Umdrehungen, welche die Welle pro Minute beim normalen
Gange des Hammers macht und aus den Umdrehungen, drehungen, die noch erfolgen,
wenn die Schütze geschlossen worden ist, das Gewicht der Schwungräder berechnen
wollten, welche jene dicken Wellen ersetzen könnten.
Da diese Formel weniger bekannt seyn mag, so wollen wir sie hier kurz entwickeln.
Es sey A B C
Fig. 5 ein Rad
mit einer Welle. Am Umfange des Rades denken wir uns eine Kraft thätig, welche den
Widerstand am Umfange der Welle, der durch den Betrieb der Arbeitsmaschine, z. B.
durch die Bewegung eines Hammers entsteht, sowie die Zapfenreibung mit
gleichförmiger Geschwindigkeit überwindet. — Ist G das Gewicht der ganzen Maschine, f der
Coefficient der Zapfenreibung, r der Halbmesser der
Zapfen und R der der Welle, so ist die auf den
Wellen-Um-Umfang reducirte Zapfenreibung:
f Gr/R(1)
Beträgt der Widerstand, welcher durch die Bewegung der Arbeitsmaschine erzeugt wird,
W, so ist der Gesammtwiderstand am Umfange der
Welle:
W + f Gr/R.
Dieser möge mit Q bezeichnet werden.
Die Winkelgeschwindigkeit der Radwelle sey w, also die
Umfangsgeschwindigkeit der Welle w
R; alsdann ist die pro
Secunde verrichtete Arbeit:
Q. wR.
Bedarf die Maschine zu ihrem Betriebe L Pferdekräfte, so
hat man:
QwR = 480 L,
da eine Pferdekraft 480 preuß. Fußpfund ist.
Hieraus ist:
Textabbildung Bd. 189, S. 189
Macht die Maschine bei gleichförmiger Geschwindigkeit in der Minute n Umdrehungen, so haben wir für w:
Textabbildung Bd. 189, S. 189
und wenn wir diesen Werth in (2) einsetzen, entsteht:
Textabbildung Bd. 189, S. 189
Hört nun die Kraft am Umfange des Rades plötzlich zu wirken auf, so setzt die Maschine
vermöge ihrer Trägheit oder lebendigen Kraft, ihre Bewegung noch weiter fort und
überwindet den Widerstand noch durch eine gewisse Wegstrecke.
Ist u die Zahl der Umdrehungen, welche die Welle noch
macht, nachdem die Kraft zu wirken aufgehört hat, so wird Q noch durch den Weg:
2 π R . u
überwunden. Es leistet also die Maschine vermöge ihrer
Trägheit noch die Arbeit:
2 π R
u . Q,
oder, wenn wir aus (3) den Werth von Q einsetzen:
Textabbildung Bd. 189, S. 190
Während sie diese Arbeit noch leistet, wird ihre ganze lebendige Kraft aufgezehrt.
Diese beträgt aber
½ w2
T,
wenn T das Trägheitsmoment der
ganzen Radwelle bezeichnet.
Da aber w = π n/30
ist, so hat man auch für jene lebendige Kraft:
½ (π n/30)2
T.
Dieser Werth muß dem unter (4) gleich seyn. Daher haben wir:
Textabbildung Bd. 189, S. 190
oder Textabbildung Bd. 189, S. 190
Endlich:
(I)
Textabbildung Bd. 189, S. 190
Pferdekräfte.
Aus dieser Gleichung erhalten wir also L, wenn wir n, u und T kennen. Die
beiden ersteren Werthe n und u lassen sich ziemlich genau und mit Leichtigkeit durch Beobachtung
finden, der Werth von T dagegen läßt sich weniger scharf
durch Vermessungen und Berechnungen ermitteln. Doch glauben wir, denselben im
Nachstehenden möglichst genau bestimmt zu haben. Uebrigens ersieht man aus der
Formel, da L mit der 3. Potenz von n wächst,
daß ein kleiner Fehler in n schon einen nicht
unbedeutenden Fehler für L bewirkt.
Wollen wir aus der letzten Formel die Arbeit berechnen, welche die Ueberwindung des
Widerstandes der Arbeitsmaschine erfordert, so haben wir davon die Arbeit
abzuziehen, welche die Zapfenreibung verzehrt.
Nach (2) ist:
Textabbildung Bd. 189, S. 191
da aber Q = W + f G r/R war,
so hat man auch:
Textabbildung Bd. 189, S. 191
= Arbeit des Widerstandes W1, + Arbeit der Zapfenreibung. Wird erstere mit L1 bezeichnet, so
ist:
Textabbildung Bd. 189, S. 191
oder Textabbildung Bd. 189, S. 191
Textabbildung Bd. 189, S. 191
Pferdekräfte (II)
Den Coefficienten f der Zapfenreibung haben wir sowohl
für die Ruhe wie für die Bewegung ermittelt.
Bezeichnen wir die Kraft am Umfange des Rades, welche der Zapfenreibung das
Gleichgewicht hält mit P, und den Halbmesser des Rades
mit R1, so haben
wir:
P R1
= f. G r.
Es ist hieraus der Reibungscoefficient der Ruhe:
Textabbildung Bd. 189, S. 191
Den Coefficienten der Bewegung können wir in ähnlicher Weise bestimmen, wie die
Betriebskraft der Maschine.
Die Radwelle mache beim Leergehen und nachdem sie eine gleichförmige Geschwindigkeit
angenommen, pro Minute wieder n Umdrehungen; alsdann ist die Winkelgeschwindigkeit w:
Textabbildung Bd. 189, S. 191
und die lebendige Kraft der Maschine:
Textabbildung Bd. 189, S. 191
unter T wieder das Trägheitsmoment
derselben verstanden.
Der Widerstand am Umfange des Zapfens ist f G. Macht die
Radwelle nun, nachdem die Schütze geschlossen worden ist, noch u Umdrehungen, so wird f G
durch den Weg 2 π r u überwunden. Daher haben
wir:
Textabbildung Bd. 189, S. 192
Oder
Textabbildung Bd. 189, S. 192
Wir werden alsbald sehen, daß dieser Coefficient nicht unbedeutend kleiner ist als
der der Ruhe.
Es erübrigt uns nun noch, das Gewicht (G) und das
Trägheitsmoment (T) der Radwelle zu bestimmen. Zu dem
Ende haben wir die einzelnen Dimensionen des Hammers, an welchem wir unsere Versuche
und Beobachtungen ausführten und den wir in den Figuren 1,3 und 6 abgebildet haben, mit
Sorgfalt bestimmt. Um aber aus denselben das Gewicht der Welle und des Rades
möglichst genau berechnen zu können, ist das spec. Gewicht des Holzes, und zwar
sowohl das des trockenen Holzes der Welle als das des Rades, welches natürlich ganz
mit Wasser durchtränkt war, vermittelst einer genauen Waage vorher sorgfältig
ermittelt worden.
Es betrug das spec. Gewicht des trockenen Holzes der Welle von den mehr nach Außen
liegenden Theilen: 0,6803.
Die mehr nach Innen liegenden Theile besitzen jedenfalls ein größeres spec. Gewicht,
so daß man wohl das mittlere spec. Gewicht des trockenen Theiles der Welle zu 0,70
annehmen kann. Vielleicht ist diese Zahl noch eher etwas zu klein als zu groß;
— hiernach wiegt denn 1 Kubikf. jenes Holzes 61,8 × 0,70 = 43,26 Pfd.,
wofür wir in runder Zahl 43¼ Pfd. setzen wollen. — Das Rad, sowie
derjenige Theil der Welle, der ganz außerhalb des Gebäudes liegt, ist, wie schon
oben bemerkt wurde, ganz mit Wasser durchtränkt. Es betrug das spec. Gewicht von
diesen Theilen: 1,162.
Hiernach würde 1 Kubikf. dieses Holzes 61,8 × 1,162 = 71,81 Pfd. wiegen, wofür
in runder Zahl 71½ Pfd. genommen werden mag.
Es beträgt nun der kubische Inhalt der beiden Theile A +
B der Welle (Fig. 6): 103,95 Kubikfuß;
der der beiden Daumenkränze D + E 22,455 Kubikf.; zusammen also 126,405 Kubikfuß. Das Gewicht dieser
Theile beläuft sich demnach auf: 126,4 × 43,25 = 5466,8 Pfd.
Der Inhalt von F beträgt 156 Kubikfuß. Davon liegen etwa
80 Kubikfuß im Gebäude und 76 außerhalb desselben. Die ersteren sind theilweise mit
Wasser durchtränkt, die anderen jedenfalls vollständig, da der Hammer schon circa 30 Jahre im Betriebe ist. Das Gewicht der ersteren läßt sich
deßhalb wohl gleich setzen: 60 × 80 = 4800 Pfd., das der anderen ist: 76
× 71½ = 5414 Pfd.
Außerdem sind noch 12 eiserne Ringe um die Welle gezogen, die ein Gesammtgewicht von
12 × 28 = 336 Pfd. besitzen.
Da ferner vor der Welle ein Sensenbreithammer und ein Reckhammer stehen, für den
ersteren 11, für den anderen 12 Daumen vorhanden sind, wovon jeder circa 30 Pfd. wiegt, so kommt zu dem vorigen noch ein
Gewicht von 23 ½ 30 = 690 Pfd.
Endlich schätzen wir das Gewicht der beiden Zapfen zu 300 Pfd.
Demnach beläuft sich das ganze Gewicht der Welle auf:
5467 + 4800 + 5414 + 336 + 690 + 300 = 17007 Pfd.
Wir ermitteln nunmehr den Inhalt und das Gewicht des Rades.
Der Inhalt der beiden Radkränze beträgt 15,57 Kubikfuß, mithin das Gewicht derselben
15,57 × 71,5 = 1113 Pfd.
Die beiden eisernen Ringe, welche die Kränze umgeben, wiegen zusammen 115 Pfd.
Der Inhalt des Radringes beträgt: 29,37 Kubikfuß, und sein Gewicht: 29,37 ×
71,5 = 2100 Pfd.
Der kubische Inhalt der 16 Schaufeln von 1 Zoll Dicke ist 8 Kubikf. und deren Gewicht
8 × 71,5 = 572 Pfd.
Der Inhalt der 8 Radarme beträgt 30,8 Kubikfuß, also das Gewicht derselben: 30,8
× 71,5 = 2202 Pfd.
Sodann kommen noch 4 eiserne Streben vor, welche zur Befestigung der Radkränze
dienen, von 1“ Durchmesser und 5 Fuß Länge; deren Gewicht beläuft sich mit
Zubehör auf circa 56 Pfd.
Hiernach erhalten wir für das ganze Gewicht des Rades:
1113 + 115 + 2100 + 572 + 2202 + 56 = 6158 Pfd.
Es beträgt also das ganze Gewicht der Radwelle: 17007 + 6158 = 23165 Pfd
Jetzt lassen sich auch leicht die Trägheitsmomente der einzelnen Theile der Maschine
bestimmen.
1) Wir berechnen zuerst das Trägheitsmoment der hölzernen Welle. Es ist: ½M r2, unter r den Radius und unter M die
Masse der Welle verstanden. Nehmen wir r zu 1,9 Fuß an,
so haben wir:
1/2 M.(1,9)2 = 1/2 . G . g(1,9)2 = 1/g . 1/2 . (1,9)2 .
15681Das Gewicht des bloßen Holzes der Welle beträgt nämlich 15681
Pfd.
= 1/g . 28303.
Hier bezeichnet bekanntlich g die Beschleunigung der
Schwere.
2) Das Trägheitsmoment der 12 eisernen Ringe, welche um die Welle gelegt sind,
ist:
M r2 = G/g r2 = 1/g . 336 . 22 = 1/g . 1344.
3) Das Trägheitsmoment der 23 Daumen wird circa
betragen:
1/g . 690 . 3,6 = 1/g . 2484
4) Für das Trägheitsmoment der Zapfen ergibt sich:
1/g . ½. 3 0 . 0,03 = 4,50.
1/g.
5) Das Trägheitsmoment der Radkränze ohne Ringe ist G/g(r2 + b2/4), wenn r der
mittlere Halbmesser und b die Breite der Kränze
bezeichnet. Man hat hierfür:
1/g . 1113 ((3,583)2 + 0,689/4) = 13,01 . 1113 1/g . 14480.
6) Die beiden eisernen Ringe haben das Trägheitsmoment:
G/g r2 = 1/g . 115. 42 = 1/g . 1840.
7) Das Trägheitsmoment der eisernen Streben ist:
1/g . 56. (3,6)2 = 1/g . 56 . 12,96 =
1/g . 726.
8) Der Radring besitzt das Trägheitsmoment: G/g(r2 + b2/4), wenn r den
mittleren Halbmesser und b die Dicke des Ringes
bezeichnet. Es ist:
1/g . 2100 (9+0,028) + 1/g . 9,03. 2100 = 1/g .
18963.
9) Das Trägheitsmoment der Schaufeln haben wir nach der Formel G/g(⅓ 12 + e2)
berechnet, worin 1 die Länge und e den kleinsten Abstand
der Schaufeln von der geometrischen Achse der Radwelle bezeichnet. Man hat
hierfür:
1/g . 572 [1/3(1,5)2 + (3,333)2 =
1/g . 572. 11,84 = 1/g .
6772
10) Das Trägheitsmoment der Radarme beträgt:
G/12g[a2 + (R - r)2 +3 (R + r2)], wenn R und r die Radien der Arme
und a die Dicke derselben ist. Wir haben hiernach:
1/g . 2202/12[(0,708)2 + (2,833 - 1,625)2 + 3 (2,833+1,625)2]
= 1/g . 11300.
Das Trägheitsmoment der ganzen Radwelle beträgt also
T = 1/g(28303 + 1344 + 2484 + 4,5 + 14480 + 1840 + 726 + 18963 + 6772 + 11300)
= 1/g . 86317 = 86317/31¼ =
2761 Fußpfd.
Wird dieser Werth von T in (I) eingesetzt, so entsteht:
Textabbildung Bd. 189, S. 195
Der Halbmesser des Zapfens der Welle beträgt 2⅛′ = 2,125′ =
0,177 Fuß. Setzt man diesen Werth von r, sowie den von
G (Gewicht der ganzen Radwelle) in (II), (III) und (IV) ein, so erhält man:
Textabbildung Bd. 189, S. 195
Oder für w: π n/30
gesetzt:
L1 =
n3/1902 u - 0,8937 f n(V)
Ferner entsteht aus (III), da R1 = 4 Fuß ist und die Umdrehungskraft P des Rades 45 bis 50 Pfd. betrug:
Textabbildung Bd. 189, S. 195
als Reibungscoefficient der Ruhe.
Endlich erhält man aus (IV) für den Reibungscoefficienten
der Bewegung:
Textabbildung Bd. 189, S. 195
Um nun diesen Coefficienten zu bestimmen, öffneten wir die Schütze und warteten, bis
die Radwelle eine gleichförmige Bewegung angenommen hatte; darnach wurde die Zahl
der Umdrehungen pro Minute beobachtet, die Schütze
geschlossen und nunmehr wurden noch die Umdrehungen gezählt, welche die Welle
machte, bis sie zur Ruhe kam.
Beim ersten Versuche betrug die Zahl der Umdrehungen pro
Minute 20 und diejenige
nach Schließung der Schütze bis die Bewegung der Welle aufhörte: 9.
Hieraus ergibt sich für f:
f = 0,00059 (20)2/9 = 0,00059 400/9
= 0,00059. 44,44 = 0,0262.
Beim zweiten Versuche war n = 21 und u = 10,4; demnach f:
f = 0,00059 (21)2/10,4 = 0,00059. 441/10,4.
= 0,00059 . 42,4 = 0,0250.
Die Art und Weise wie die Zapfen in ihren Lagern ruhen, ist in Fig. 7 (I und II) abgebildet, wovon
I die obere Ansicht und II den verticalen Durchschnitt eines Lagers sammt seinem Zapfen darstellt.
Die Zapfen sind bei c, also in der Gegend der Welle,
etwas dicker als bei d, besitzen daher eine etwas
conische Form. Die ebene Fläche d berührt das Lager
nicht mehr, wenn die Welle mehrere Wochen gelaufen hat und die Maschine, wenn wir so
sagen sollen, eine normale Lage besitzt. — Bei e
lag eine Masse Schweinefett, die zum Theil über den Zapfen reichte und vermittelst
eines Holzes, das den oberen Theil des Zapfens bedeckte, über demselben gehalten
wurde. Zudem leitete eine Rinne beständig Wasser auf beide Zapfen.
Man sieht, daß diese Construction von der der gewöhnlichen Lager, wie sie im
Maschinenwesen Anwendung finden, abweicht, und aus diesem Grunde vermag ich es nur
zu erklären, daß der gefundene Reibungscoefficient ungleich kleiner ist, als er in
der Regel, gestützt auf die Beobachtungen von Morin,
angenommen wird.
Wir bemerken übrigens noch, daß Zapfen und Lager ungefähr 15 Jahre auf einander
gelaufen hatten, und daß in Folge dessen die Lager jedenfalls etwas ausgelaufen
waren.
Unsere Versuche zeigen also, daß, ähnlich wie bei der
gleitenden Reibung ebener Flächen, der Reibungcoefficient der Bewegung fast nur
halb so groß ist als der der Ruhe.
Man kann nun auch leicht die Zeit berechnen, welche die Welle nothwendig hat, um aus
einer gewissen Winkelgeschwindigkeit w wieder zur Ruhe
zu kommen.
Wir denken uns eine Masse M = G/g im Abstände l,
welche mit der Radwelle gleiches Trägheitsmoment und gleiche Winkelgeschwindigkeit
also auch gleiche
lebendige Kraft besitzt. Wir haben hierfür:
M . l2 = G/g
l2 = T = 2761.
Am Umfange des Zapfens beträgt die widerstehende Kraft, wenn wir den
Reibungscoefficienten zu 0,0262 annehmen: 23165 × 0,0262 = 507 Pfd., also im
Abstände 1:
Textabbildung Bd. 189, S. 197
Es ist hiernach die Verzögerung (p) der
Geschwindigkeit:
Textabbildung Bd. 189, S. 197
Der Weg (s), auf welchem die Winkelgeschwindigkeit w allmählich aufgezehrt wurde, beträgt nach dem ersten
Versuche:
s = 2 . 3,1416 . 9 = 56,549 Fuß.
Somit ist also die Zeit (n), innerhalb welcher die Welle
zur Ruhe kam:
Textabbildung Bd. 189, S. 197
Obgleich wir diese Zeit nicht direct beobachtet haben, so glauben wir doch, daß die
Berechnung mit der Wahrheit fast ganz genau übereinstimmt.
Wir wenden uns nunmehr zur Bestimmung der Betriebskraft der Hammerwerke.
Wie schon oben bemerkt, standen vor der Welle jenes Hammerwerkes, an welchem wir
vorzüglich die Betriebskraft ermittelt haben, zwei Hämmer, ein schwererer
Sensenbreithammer und ein leichterer Reckhammer, unter welchem der Stahl für die
Sensenblätter zu den erforderlichen Dimensionen ausgereckt wurde. An diesem
letzteren haben wir besonders unsere Versuche ausgeführt.
Das Gewicht des eigentlichen Hammers oder des Hammerkopfes betrug 68 Pfd.; das der
Hülse 220 Pfd.; das Helmband hatte ein Gewicht von 48 Pfd., der Helm, welcher sehr
trocken war, ein solches von ungefähr 130 Pfd. Die Entfernung von der Mitte des
Helmbandes bis zur Mitte der Hülse betrug 20 Zoll, und die von letzterer bis zu der
des Hammerkopfes 41 Zoll, so daß demnach fast ganz genau ⅔ des sogenannten
Geschläges vor der Hülse lag. Die Hubhöhe des Hammers belief sich auf 6½ Zoll
und die Aufhebungskraft vorn am Hammerkopfe betrug 90 Pfd., worin die Kraft zur
Ueberwindung der Reibung zwischen Hülse und Pfadeisen mit enthalten ist.
Nehmen wir an, der Hammer werde bei jedem Hübe vom Daumen auf eine Höhe von 5 Zoll
gehoben — was von der Wahrheit sehr wenig abweichen wird — und steige
dann noch, vermöge der erhaltenen Geschwindigkeit auf den noch übrig bleibenden
Theil der Höhe von 1½ Zoll, so würde das Kraftmoment zum langsamen Aufheben
des Hammers 5/12 . 90 = 37,5 Fußpfd. betragen. Die Daumenkraft zum Niederdrücken des
Helmbandes mochte sich nach unseren Versuchen im Mittel auf 90 Pfd. belaufen und der
Weg der Reibung zwischen Daumen und Helmband auf 7 Zoll. Setzen wir den
Reibungscoefficienten = 0,15, so verzehrt diese Reibung bei jedem Schlage eine
mechanische Arbeit von 0,15 . 7/12 . 90 = 7,875 Fußpfd. Es beansprucht also im
Ganzen jeder Schlag, wenn wir von der Arbeit absehen welche zur Ertheilung von
Geschwindigkeit nothwendig ist, eine Arbeit von 37,5 + 7,875 = 45,375 Fußpfd.
Diese Zahl vermindert sich beim Schmieden offenbar, da hier die Hubhöhe des Hammers
wegen der Dicke der Hitze stets geringer ist als 6½ Zoll.
Bei den drei ersten Versuchen, welche wir behufs Bestimmung der Betriebskraft
anstellten, wurde ein Holz von circa ¾ Zoll Dicke
unter den Hammer gehalten, so daß die Hubhöhe desselben beim Arbeiten
6½–¾ = 5¾ Zoll betrug. Der Daumen hob also hiernach den
Hammer nur auf eine Höhe von 5–¾ = 4¼ Zoll. Das dazu
erforderliche Kraftmoment war also nicht 37,5, sondern 4¼/12 . 90 = 32
Fußpfd. beinahe. Rechnen wir hierzu noch die mechanische Arbeit von 7,875 Fußpfd.,
welche die Reibung zwischen Helmband und Daumen verschlingt, so erhalten wir bei
diesen Versuchen für das langsame Aufheben des Hammers ein Moment von 39,875 Fußpfd.
pro Schlag, wofür wir in runder Zahl 40 Fußpfd.
setzen wollen. Bei den beiden folgenden Versuchen wurde ein weißglühendes Eisen von
circa
1 Zoll Breite und ½ Zoll Dicke ausgereckt, wofür
wir dasselbe Moment in Rechnung bringen wollen.
Es beträgt nun ferner nach unserer Berechnung die auf den Daumen-Angriffspunkt
reducirte Masse (M1) des
Hammers 14,67. Dieselbe ist also weit geringer als die ebendahin reducirte Masse
(M) der Radwelle. Letztere beträgt nämlich
2761/(1,91)2 = 2761/3,648 = 757, da 2761 das
Trägheitsmoment der Welle und 1,91 Fuß der Radius des Daumenkranzes ist. Der
Ungleichförmigkeitsgrad in der Bewegung der Achse ist demnach sehr gering, und der
Verlust an Geschwindigkeit durch den Stoß zwischen Helmband und Daumen unbedeutend.
Man darf deßhalb annehmen, daß die Welle nach dem Stoße die mittlere Geschwindigkeit
v besitze und daß der Verlust an lebendiger Kraft,
welcher durch den Stoß entsteht, gleich der lebendigen Kraft des Hammers sey. Ist
aber die Geschwindigkeit der Welle nach dem Stoße = v,
so wird das Helmband oder die Masse M1 des Hammers mit der Geschwindigkeit v . cos 44° = 0,7193.
v bewegt (wie wir dieß früher erörtert haben), der
Verlust an lebendiger Kraft für jeden Schlag beträgt mithin: ½M1 (0,7193. v)2 = 0,259 M1
v2. Oder, da M1 = 14,0 7 ist: 0,259 . 14,67v2 = 3,799 . v2 Fußpfd., wofür wir 3,8 . v2 Fußpfd. setzen
wollen.
Da der Umfang der Welle 12 Fuß betrug, so ist v, wenn die
Welle in der Minute n Umdrehungen macht: 12. n/60. Da aber auch in der Welle 12 Daumen enthalten
waren, so hat man für die Zahl (a) der Schläge in der
Secunde, bei u Umdrehungen pro Minute: a = 12 . u/60. Es ist daher a = v, d. h. die Zahl der Schläge in der Secunde drückt auch die mittlere
Geschwindigkeit v der Welle aus. Man kann daher auch den
Verlust an lebendiger Kraft für jeden Schlag, der durch den Stoß entsteht, = 3,8.
a2 setzen. Da nun
a Schläge in der Secunde der erfolgen, so beträgt
der secundliche Verlust:
3,8. a2. a = 3,8. a3.
Es wächst demnach der Verlust durch den Stoß mit der 3. Potenz
aus der Zahl der Schläge.
Oben sahen wir, daß auch die Betriebskraft (L) mit der 3.
Potenz aus der Zahl der Umdrehungen in der Minute wachse.
Die ganze Arbeit, welche hiernach unser Hammer für das langsame Aufheben und für die
Erreichung seiner Geschwindigkeit in Anspruch nimmt, beträgt also per Secunde bei a
Schlägen:
(VI) L1 = 40. a +
3,8 . a3 = (40 + 3,8 .
a2) a Fußpfd.
Wir werden weiter unten diese Betriebskraft mit derjenigen vergleichen, welche wir
aus unseren Versuchen nach der früher entwickelten Formel L = n3/1902
. u berechnen.
Folgendes sind nun die Resultate unserer Versuche.
IVersuch.
Es war n = 14,5 und u = 2
1/12 = 2,083.
Demnach ist L. = (14,5)3/1902 . 2,083 = 0,769 Pferdekräfte.
Nehmen wir den Reibungscoefficienten der Radwelle zu 0,025 an, so erhalten wir für
die Arbeit, welche die Zapfenreibung der Radwelle verzehrt, nach Formel (V): 0,8937 . 0,025 . 14,5 = 0,322 Pferdekräfte.
Es bleiben demnach zur Bewegung des Hammers noch
L1 =
0,769 - 0,322 = 0,447 Pferdekräfte übrig.
Da die Zahl der Schläge im vorliegenden Falle pro Secunde
12 . 14,5/60 = 2,9 beträgt, so hat man nach Formel (VI):
L1
=[40 + 3,8 . (2,9)2] . 2,9 = 208,68 Fußpfd. =
0,435 Pferdekräfte, was mit dem obigen Resultate fast vollständig übereinstimmt.
II. Versuch.
Es war n = 18 und u =
2⅔ = 2,667. Daraus findet man:
L = (18)3/1902. 2,667 = 5832/1902. 2,667 = 1,149 Pferdekräfte.
Die Zapfenreibung beträgt:
0,8937 × 0,025 . 18
= 0,402 Pferdekräfte.
Daher
L1 = 1,149 - 0,402
= 0,747 Pferdekräfte.
Die Zahl der Schläge pro Secunde betrug 12. 18/60 = 3,6.
Es ist daher auch:
L1=
[40+3,8(3,6)2] . 3,6 Fußpfd. = 321,48
Fußpfd.
= 0,67 Pferdekräfte.
Der Unterschied beträgt 0,077 Pferdekräfte, also jedenfalls nicht mehr, als er durch
Beobachtungs- und Rechnungsfehler seyn kann.
III. Versuch.
Für n ergab sich 22, für u:
3¼ = 3,25 . Man findet:
L = (22)3/1902 . 3¼ = 10648/1902 . 3¼ = 1723 Pferdekräfte.
Die Arbeit der Zapfenreibung beträgt:
0,8937 × 0,025 . 22 = 0,492 Pferdekräfte,
mithin:
L1 =
1,723 - 0,492 = 1,231 Pferdekräfte.
Die Zahl der Schläge pro Secunde belief sich auf 12.
22/60 = 4,4. Somit ist auch:
L1 =
[40 + 3,8 (4,4)2 . 4,4 = 1,041 Pferdekräfte.
Der Unterschied beträgt also 1,231 - 1,041 = 0,19 Pferdekräfte.
IV. Versuch.
Man hatte für n: 24 und für u: 3 5/6 = 3,833.
Also ist:
L = (24)3/1902 . 3,833 = 13824/7290 = 1,896 Pferdekräfte.
Nehmen wir wieder f zu 0,025 an, so erhalten wir für die
Arbeit der Zapfenreibung: 0,8937 . 0,025 . 24 = 0,535 Pferdekräfte, daher:
L1 =
1,896 - 0,535 = 1,361 Pferdekräfte.
Es ist ferner a 24 . 12/60 = 4,8; mithin auch
L1
= [40 + 3,8 . (4,8)2 . 4,8 = 611,5 Fußpfd. = 1,48
Pferdekräfte. Auch hier ist der Unterschied nicht größer, als er zufolge der
Beobachtungsfehler seyn kann.
Als ich zwei bis drei Wochen später an demselben Hammer Versuche anstellte, waren
verschiedene Reparaturen vorgenommen, unter Anderem war die Hammerwelle etwas tiefer
gelegt und die Zapfenlager waren mehr angetrieben worden, so daß sie die ebenen
Flächen der Zapfen scharf berührten. Ich fand jetzt:
V. Versuch
für n = 23,5 und für u = 2,333.
Hieraus ist L = 2,928 Pferdekräfte.
Die Zahl der Schläge in der Secunde betrug 12 . 23,5/60 = 4,7; daher war die
Betriebskraft für die Bewegung des Hammers
L1 =
[40 + 3,8 . (4,7)2] 4,7 = 582 Fußpfd.
Da der Hammer etwas höher lag als bei den vorhergehenden Versuchen, so war der
Verlust durch Stoß größer; wir setzen daher
L1 =
610 Fußpfd. = 1,271 Pferdekräfte.
Demnach würde die Zapfenreibung eine Arbeit von 2,928 - 1,271 = 1,657 Pferdekräfte in
Anspruch genommen haben. Vorhin betrug diese Arbeit für 24 Umdrehungen in der Minute
nur 0,535 Pferdekräfte, sie ist also in dem vorliegenden Versuche mehr als dreimal
so groß; mithin war der Coefficient der Zapfenreibung etwas mehr als 3 ×
0,025 = 0,075, was mit den Ermittelungen Morin's genau
übereinstimmt.
Die eigentlichen Stahlraffinirhämmer, welche besonders zum Plätten oder Schienen,
sowie zum Raffiniren des Rohstahles dienen und die, wie schon früher erwähnt, ein
Gewicht von 50 bis 70 Pfd. und eine Hubhöhe von 7 bis 8 Zoll besitzen, machen beim
Plätten circa 360 und beim Zusammenschweißen oder
Raffiniren 380 bis 400 Schläge in der Minute. Im ersteren Falle werden die Hämmer
auf eine Höhe von 6½ bis 7½ Zoll, im anderen von ungefähr 3½
bis 4½ Zoll gehoben, da in beiden Fällen die Dicke der Hitze von der ganzen
Hubhöhe zu subtrahiren ist.
Nach meinen Erfahrungen machen nun die Wellen dieser Hämmer, welche meistens 10
Daumen enthalten, wenn beim Plätten die Schütze geschlossen wird, noch 5 bis 6
Umdrehungen, während sich diese Zahl beim normalen Gange auf 36 beläuft. Die
wenigsten Wellen dieser Hämmer besitzen aber die Dicke und also auch das
Trägheitsmoment, das die Welle unseres Hammers besitzt, an welchem wir die oben
angeführten Versuche angestellt haben. Wir dürfen annehmen, daß dasselbe circa um 1/5 geringer ist. Unsere Formel für die
Betriebskraft würde demnach in folgende übergehen:
L = n3/2880 . u,
oder, wenn wir uns der Logarithmen bedienen:
log L
=
3 log n - (log
2880 + log u)
=
3 log n - (3,3579 + log
u).
Nehmen wir nun für's Plätten n = 36 und u = 6, so erhalten wir:
log L = 3 log 36 - (3,3579 +
log 6) = 3,410 Pferdekräfte.
Diese Zahl wird von der Wahrheit nicht um 10 Proc. abweichen.
Für's Zusammenschweißen dürfen wir setzen: n = 38 und u = 9. Alsdann ist:
log L = 3 log 36 - (3,3579 +
log 9) = 2,675 Pferdekräfte.
Der Verlust durch den Stoß ist hier geringer als beim Plätten, weil wegen der weit
dickeren Hitze (3 bis 3½″) der Winkel (α + β) ungleich
größer ist als wir ihn oben gefunden haben, weßhalb also auch die Geschwindigkeit,
mit der der Hammer gehoben wird, geringer seyn muß. Sodann ist auch, der kleineren
Hubhöhe wegen, die mechanische Arbeit zum langsamen Aufheben des Hammers
unbedeutender als vorhin.
In der That erhalten wir fast ganz genau die oben berechnete Betriebskraft für den
vollen Gang des Hammers, wenn wir dieselbe aus der Menge und Geschwindigkeit des
Aufschlagwassers ermitteln.
Es betrug bei einem Versuche, welchen ich vor mehreren Jahren anstellte, die Zahl der Schläge pro Minute 380; dabei war die Schütze 5¼ Zoll
hoch gezogen, während dieselbe eine Breite von 26 Zoll besaß und die Druckhöhe im
Wassergerinne sich auf 3′ 8″ = 3,667 Fuß belief. Die Neigung der
Schußrinne gegen den Horizont betrug circa
28½°, so daß man die schräge Höhe der Schützenöffnung noch mit. cos 28½ = 0,879 zu multipliciren hat, um die
senkrechte zu finden. Da ferner die Welle 10 Daumen enthielt, so machte sie in der
Minute 380/10 = 38 Umdrehungen.
Ist nun C die Geschwindigkeit, mit welcher das Wasser auf
die Schaufeln des Rades trifft, v die
Umfangsgeschwindigkeit des Rades an dieser Stelle, α aber der Winkel, welchen
die Richtung des stoßenden Wasserstrahles mit der Bewegungsrichtung des Rades
einschließt, so hat man bekanntlich für die mechanische Leistung (L) des Wassers durch den Stoß:
L = 61,8/9 Q(c cos α - v) v Fußpfd.,
wenn 61,8 Pfd. das Gewicht von 1 Kubikfuß Wasser und 9 Fuß die
Endgeschwindigkeit eines freifallenden Körpers am Ende der 1. Secunde bezeichnet. Da
g = 31¼ Fuß ist, so hat man auch:
L
=
1,978 Q(c cos
α - v) v
Fußpfd.,
oder
L
=
1,978/480 Q (c cos
α - v) v
=
0,00412 Q (c cos
α - v) v
Pferdekräfte.
Bezeichnen wir nun die senkrechte Höhe von der Mitte der Schützenöffnung bis zu dem
Punkte wo der stoßende Wasserstrahl die Schaufeln trifft, mit h1, den Ausfluß- oder
Geschwindigkeitscoefficienten des Gerinnes mit β, so haben wir
bekanntlich:
Textabbildung Bd. 189, S. 203
Nach unseren Untersuchungen dürfen wir bei der in Rede stehenden Druckhöhe und
Schützenöffnung für β setzen 0,96 bis 0,97. Nehmen wir den ersteren Werth, so
erhalten wir:
Textabbildung Bd. 189, S. 203
Da nun die senkrechte Höhe der Schützenöffnung 5,25 × 0,879 = 4,615 Zoll =
0,386 Fuß betrug, so war h = 3,667 - ½ . 0,386 =
3,667 - 0,193 = 3,474 Fuß.
Ferner ist h1, im
Durchschnitt 2 + ½ . 0,386 = 2,193 Fuß. Demnach
Textabbildung Bd. 189, S. 203
C = 18,336 Fuß.
Dabei ist freilich von dem Verluste der Geschwindigkeit auf der Schußrinne
abgesehen.
Die Geschwindigkeit des Wassers beim Ausfluß aus der Schützenöffnung war:
Textabbildung Bd. 189, S. 204
Für die Wassermenge Q, welche in jeder Secunde zum
Ausfluß gelangt, erhalten wir daher:
Q = 2,17 × 0,386 × 14,137 = 11,847
Kubikfuß, da die Breite der Schützenöffnung 26 Zoll = 2,17 Fuß betrug.
Das Rad hatte einen Durchmesser von 8 Fuß und eine Ringtiefe von 1 Fuß. Der Radius
des Punktes wo der mittlere Wasserstrahl die Schaufeln traf, mochte 3⅔ Fuß,
also der Umfang hierfür 2 . 3,1416 × 3,667 = 23,022 Fuß betragen. Da diese in
der Minute 38 mal durchlaufen wurden, so war:
v = 23,022 × 38/60 = 14,58
Fuß.
Da α beinahe = 0 ist, so hat man:
L = 0,00412 . 11,847 (18,336 - 14,58) . 14,58 = 0,00412 .
11,847 . 3,756 . 14,58 = 2,674 Pferdekräfte, genau wie oben.
Eine Druckwirkung des Wassers kann hier unmöglich stattfinden. Ist nämlich G das Gewicht des Wassers in einer Zelle, so z. B. in
der zwischen den Schaufeln a und g, so beträgt die Centrifugalkraft desselben, bei 38 Umdrehungen pro Minute und dem mittleren Halbmesser von 3,5 Fuß:
P
=
0,0003509 . (38)2 . 3,5 . G
=
0,0003509 . 1444 . 3,5 . G
=
1,7734 . G.
Ist nun a b, Fig. 3; die Größe dieser
Kraft, so können wir uns diese in die beiden Seitenkräfte a
c und a d zerlegt denken, von denen die erstere
der Schwerkraft G entgegenwirkt und die andere gegen die
Schaufel drückt. Da für die Schaufelstellung bei a der
Winkel c a b nach unserer Messung 28½°
beträgt, so hat man:
a c
=
a b. cos
28½ = 0,879 . a b
und
a d
=
b c = a b . sin
28½ = 0,477 . a b.
In der Zelle zwischen a und f
kann das Wasser diesen Kräften nicht folgen, dieß hindert der stoßende Wasserstrahl
und die schräge Lage der Schaufeln. Gelangt aber die Schaufel a allmählich in die Lage von g, so kann eine
Entleerung der Zelle stattfinden. Da a b = P = 1,7734 . G ist, so
ergibt sich für
a c: 1,7734 . 0,879 . G
=
1,5588 . G
und für
a d: 1,7734 . 0,477 . G
=
0,8457 . G.
Bezeichnet die Linie a h das Gewicht G des Wassers und macht man c
i = a h = G, so
repräsentirt a i die Kraft, welche dem Wasser
Geschwindigkeit nach oben ertheilt. Diese beträgt also P
- G = 1,5588 × G -
G = 0,5588 . G und wird
auf dem Wege von a nach g
immer kleiner. Da für die Schaufelstellung g der c a b nach unserer Messung 49½° beträgt,
so hat man hierfür:
a c = a b
. cos 49½° = 0,649 . 1,773 . G = 1,1507 . G.
Dagegen wird die Seitenkraft a d größer und beträgt:
a d = a b
. sin 49½° = 0,760 . 1,773 . G = 1,347 . G.
Vereinigt man die beiden Kräfte a i und a d zu einer Mittelkraft a
k, so repräsentirt diese die Größe und Richtung derjenigen Kraft, mit welcher
der Wasserkörper aus der Zelle getrieben wird. Für die Schaufelstellung a hat man:
Textabbildung Bd. 189, S. 205
Natürlich hätte man diese Kraft auch erhalten, wenn man ab und ah, also die Centrifugal- und
Schwerkraft zu einer Mittelkraft vereinigt hätte.
Bei g beträgt die Mittelkraft ak:
Textabbildung Bd. 189, S. 205
sie wird also zwischen a und g immer größer. Nehmen wir aus beiden das Mittel, so
erhalten wir ak = 1,232 G.
Wird ferner ka verlängert, bis zum Durchschnitt mit der
Mittellinie m n des Rades, so erhalten wir in 1 den
Punkt, dessen Abstand vom Mittelpunkte o der Radwelle
nach der Formel 2850/u2 zu berechnen ist, wenn u die Zahl der
Radumdrehungen pro Minute bezeichnet. Ziehen wir von 1
die Strahlen 1p, 1q, 1r, so bezeichnen diese die Richtungen in welchen die
Wassertheilchen aus der Zelle a g fliehen, und zwar mit
der durchschnittlichen Beschleunigung
p = 1,355 . G/G . g = 1,355 .
31¼ Fuß = 42,14 Fuß.
Da eine Schaufel, um von a nach g zu kommen, 0,091 Secunden gebraucht, so legen die Wassertheilchen in
dieser Zeit nach jenen Richtungen einen Raum von = (0,091)2 . ½ . 42,14 Fuß = 0,17 Fuß zurück, sie
werden also auf dem Wege von a nach g theilweise wieder in die Zelle fallen. Dagegen werden
nun, wenn die Schaufeln von g nach s gelangen, diese Wege immer größer, so daß hier die
vollständige Entleerung der Zellen stattfindet.
Da das Wasser in den Zellen eine lose Masse bildet, die mit den Radtheilen nicht fest
verbunden ist, so ziehen sich die Schaufeln schnell unter der Wassermasse weg;
sobald dieß aber geschehen ist, treten die oben berechneten Kräfte, die in den
Richtungen 1q, 1r, etc.
thätig sind, als momentane Kräfte auf und vereinigen sich mit der stetig wirkenden
Schwerkraft, wodurch also die Wassertheilchen in den in der Figur gezeichneten
Parabelbogen herunterfallen.
Es gewährt in der That einen sehr prächtigen Anblick, wenn man vor einem solchen sich
schnell drehenden Rade steht, und den stoßenden, in der Mitte krystallhellen
Wasserstrahl, sowie die von dem Rade abspritzende schneeweiße, schaumartige
Wassermasse betrachtet, wobei man dann in unmittelbarer Nähe das ungeheure Getöse
des Hammers hört. Vom ökonomischen Standpunkte aus ist die Erscheinung dagegen sehr
zu beklagen. Denn da das ganze Gefälle im vorliegenden Versuche stark 13 Fuß betrug,
so entsprach dieses einer mechanischen Arbeit von 13 × 11,847 × 61,8
Fußpfd. = 19,83 Pferdekräften; es belief sich demnach der Wirkungsgrad des Rades nur
auf 2,674/19,83 = 0,135. (So wird also das Wasser bei diesen Hammerwerken auf eine
unverzeihliche Weise verschleudert, und man hätte daher auf eine gänzliche
Umänderung derselben wohl Bedacht zu nehmen.)
Wir führten oben an, daß in dem Werke: „Untersuchungen über den Effect
einiger in Rheinland-Westphalen bestehenden Wasserwerke“ außer
der mitgetheilten noch eine zweite Tabelle enthalten sey, welche die Radumdrehungen
für eine bestimmte Schützenöffnung beim Betriebe des Hammers enthalte und die mit
unseren Beobachtungen sehr wohl übereinstimme. Wir lassen dieselbe hier folgen.
Textabbildung Bd. 189, S. 206
Nummer des Versuches; Ganzes
Gefälle; Schützen-Oeffnung,; Breite; Höhe nebst
Reductions-Coefficient; Druckhöhe; Kraftmoment; Zeit eines Radumlaufes;
Schläge pro Secunde.
Wir sehen hieraus, daß schon bei einer Schützenöffnung von 9″′ Höhe die
Zahl der Radumdrehungen sich auf 60/3,05, also auf 19 bis 20 belief, während sie
nach der früheren Tabelle bei einer Höhe der Schützenöffnung von dem 23,5/9 =
2,61fachen nur 60/3,59 = 16 bis 17 betrug.
Nun war hierfür das Effectmoment 1917 Fußpfd., es würde also bei 9″′
Höhe, unter übrigens gleichen Verhältnissen, nur 1917/2,61 gewesen seyn. Aber der
Wirkungsgrad der Hammerräder vermindert sich mit der Zahl der Radumdrehungen sehr
schnell, so daß man für das Effectmoment vielleicht nur 1700/2,61 = 651,3 Fußpfd.,
oder, da 1 Pferdekraft hier zu 510 Fußpfd. angenommen ist, 651,3/510 = 1,27
Pferdekräfte gefunden hätte. Wir haben oben bei unserem II. Versuche für 3,6 Schläge pro Secunde (also
für 3,6 - 3,3 = 0,3 Schläge mehr), aber für eine vortheilhaftere Umdrehungszahl (18
pro Minute) ein Effectmoment von 1,149 Pferdekräften
gefunden, was also mit jener Zahl recht genau übereinstimmt.
Vergleichen wir den 3. Versuch dieser Tabelle mit dem 7. der ersten, so finden wir,
daß die Höhen der Schützenöffnungen um ¼ Zoll verschieden sind. Dagegen
beträgt hier die Zeit eines Radumlaufes 1,96 Secunden und dort 3,47, also beinahe
doppelt so viel. Nehmen wir nun an, das Effectmoment habe bei jenem 7. Versuche bei
25,6 Linien Höhe der Schützenöffnung 2100 Fußpfd. betragen, so würde es bei der
Dauer von 1,96 Secunden pro Radumlauf jedenfalls nur
halb so viel, also 1050 Fußpfd. = 1050/510 = 2,06 Pferdekräften gewesen seyn, da
jedenfalls der Wirkungsgrad des Rades nur die Hälfte betragen hätte. Wir erhielten
bei unserem IV. Versuche für 4,8 Schläge pro Secunde 1,896 Pferdekräfte.
Hieraus geht mir unzweifelhaft hervor, daß diese 2. Tabelle die Richtigkeit meiner
Versuche vollständig bestätigt.
Wir wenden uns nun zur Untersuchung über die Betriebskraft der Sensen- und
Sägenbreithämmer.
Jener Sensenbreithammer, der mit dem früher erwähnten Reckhammer vor einer Achse
stand, machte beim Fertigbreiten in der Minute 210 Schläge, wobei der Daumenkranz 11
Daumen enthielt.
Die Zahl der Umdrehungen (n) betrug also 210/11 = 19. Als
die Schütze geschlossen wurde, machte die Welle noch (u
=) 2,5 Umdrehungen. Wir haben demnach aus der Formel
L = n3/1902 . u, (19)3/1902 . 2,5 = 1,443 Pferdekräfte.
Beim sogenannten Durchbreiten beträgt die Zahl der Schläge in 240 der Minute 240,
also die der Radumläufe 240/11 = 22 beinahe. Wird die Schütze geschlossen, so macht
die Welle noch 3 Umdrehungen bevor sie zur Ruhe kommt. Demnach ist:
L = (22)3/1902 . 3 = 1,866 Pferdekräfte.
Die Sägenbreithämmer, welche wie die vorigen ein Gewicht von 90 bis 100 Pfd., dagegen
ein etwas kürzeres Geschläge, sowie einen Hub von 4 bis 4½ Zoll besitzen,
machen beim vollen Gange circa 460 Schläge in der
Minute. Da die Wellen 13 Daumen enthalten, so beläuft sich die Zahl der
Radumdrehungen für diesen Fall auf 460/13 = 35,385.
Die Räder besitzen deßhalb eine etwas vortheilhaftere Geschwindigkeit als die der
Stahlraffinirhämmer beim vollen Gange. Demnach wird auch der Nutzeffect des Rades
und die auf dasselbe übertragene Arbeit, unter übrigens gleichen Umständen, etwas
größer seyn. Man kann nun rechnen, daß die Wellen nach Schließung der Schütze noch 7
Umdrehungen machen. Hiernach wäre, bei Zugrundelegung der Formel
L = n3/2880 . u, L = (35,385)3/2880 . 7
= 3,33 Pferdekräften.
Also dieselbe Kraft, welche ein Stahlraffinirhämmer beim Plätten in Anspruch nimmt.
Man weiß auch aus Erfahrung, daß beide Arten von Hammerwerken circa dieselbe Kraft zu ihrem Betriebe bedürfen, und daß man einen
Sägenbreithämmer leicht in einen Stahlraffinirhammer oder umgekehrt, umändern kann;
Wassergerinne und Rad darf man dabei vollständig ungeändert lassen.
Schließlich wollen wir nun die Hauptergebnisse der vorstehenden Untersuchungen
übersichtlich zusammenstellen.
1) Die Reibungscoefficienten der hiesigen Hammerwellen betragen:
a) für die Ruhe 0,049 bis 0,044;
b) für die Bewegung 0,025 bis
0,026.
Dieser Coefficient erreicht aber zuweilen den Werth 0,075 bis 0,08.
2) Der Wirkungsgrad der Wasserräder schwankt nach meinen früheren und den jetzigen Untersuchungen
zwischen ungefähr 0,45 und 0,135; im letzteren Falle sind die Räder reine Stoßräder.
3) Die Betriebskraft der Sensenbreithämmer ist am kleinsten; sie beträgt bei dem
Reibungscoefficienten 0,025 circa 1½ bis 2
Pferdekräfte.
4) Die Stahlraffinirhämmer beanspruchen beim Plätten eine Arbeit von 3½, beim
vollen Gange von 2¾ Pferdekräften.
5) Für Sägenbreithämmer darf man dieselbe Betriebskraft rechnen.
6) Diese Betriebskräfte können sich leicht um 1 bis 2 Pferdekräfte vermehren, wenn
der Reibungscoefficient der Wellen größer wird.
Remscheid, im Juni 1868.
Tafeln