| Titel: | Ein Diaphanometer zu praktischen Messungen; von Ferdinand Ticinsky. |
| Autor: | Ferdinand Ticinsky |
| Fundstelle: | Band 192, Jahrgang 1869, Nr. LI., S. 199 |
| Download: | XML |
LI.
Ein Diaphanometer zu praktischen Messungen; von
Ferdinand
Ticinsky.
Mit Abbildungen auf Tab.
IV.
Ticinsky's Diaphanometer zur Bestimmung der Durchsichtigkeit
verschienener Glassorten.
Die rasche und einfache Bestimmung der Durchsichtigkeit verschiedener Glassorten
dürfte für die meisten Zwecke sehr wünschenswerth seyn.
Mein hierzu dienendes Instrument stützt sich zunächst aus den Lehrsatz, daß die
Lichtstärke einer Lichtquelle im quadratischen Verhältniß der Distanzen ab-
und zunimmt, und ferner aus die Erscheinung, daß ein früher durch Glasscheiben
geleitetes Lichtbündel aus einem weißen Schirm einen lichten Flecken erzeugt, dessen
Lichtintensität der Durchsichtigkeit des Glases entspricht.
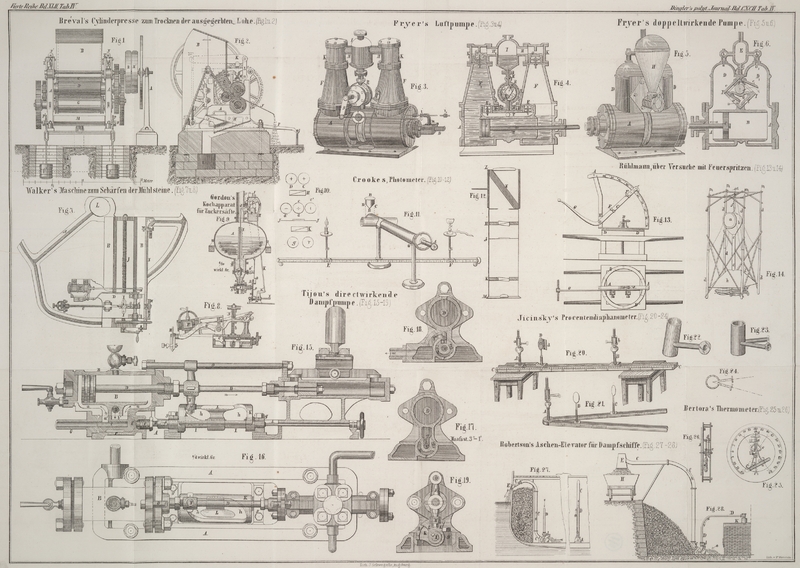
Die äußere Form des Diaphanometers ist, wie Fig. 20 zeigt, dieselbe
wie jene des Bunsen'schen Photometers und es kann jedes
Bunsen'sche Photometer mit einigen Abänderungen zu
diaphanometrischen Messungen benutzt werden.
A und B,
Fig. 20, ist
ein und dieselbe Lichtquelle in zwei Exemplaren. Am besten eignen sich dazu
Petroleumlampen. a und b
sind geschwärzte Cylinder, jeder mit einem Tubus von etwa 2 Centimeter Durchmesser
und 6—8 Centimeter Länge. Diesen Cylinder, welcher beim Versuch über die
Flamme geschoben wird, zeigt Fig. 22 im Detail. Darin
ist am Ende des Tubus eine Kreisscheibe mit zwei Federn ersichtlich, welche den Zweck haben, ein
auch unregelmäßig geformtes Stück einer Glasscheibe festzuhalten und an den Tubus
anzudrücken. D ist ein vollkommen undurchsichtiger
weißer Schirm; d ist ein Theil des Winkelspiegels,
welcher mit dem zweiten in der Zeichnung unsichtbaren Flügel einen Winkel von
90° einschließt. Dieser Winkelspiegel ist mit einer kleinen Quetschpincette
an den Schirm D befestigt und kann somit leicht
ausgesetzt und wieder abgenommen werden. C, C ist der
rinnenförmige Maaßstab in einer Länge von 6—8 Fuß, welche noch in Zehntel
eingetheilt sind. Diese Theilung reicht vollständig hin. Wollte man auch Hundertel
ablesen können, so müßte noch aus dem Fuße von A und B ein entsprechender Nonius angebracht werden. Die
Theilung ist ferner so eingerichtet, daß der zweite Fußtheilstrich vom linken Ende
des Maaßstabes mit 0 bezeichnet ist, während die Ziffern
von da ab nach beiden Seiten numerisch fortschreiten. Daß die Lichtquellen A und B verschiebbar sind,
versteht sich von selbst.
Der Schirm D muß aus den Theilstrich O eingestellt seyn und ist unbeweglich für alle
Messungen. Aus der Theilung ist auch ersichtlich, daß die Lichtquelle A nur in engen Grenzen verschiebbar seyn kann, während
nch die Lichtquelle B in einer bedeutenden Dimension
bewegt. Die Versuche müssen in einem dunklen Zimmer ausgeführt werden.
Aus den Tubus des Lichtes A steckt man ein wenig
durchsichtiges dunkles Glas, dessen Durchsichtigkeit zu 1 angenommen wird. Aus den
Tubus des Lichtes B steckt man die zu prüfende
Glasscheibe. Wenn nun das Licht A aus dem Theilstrich 1
und der Schirm aus O steht, so entsteht aus einer Seite
des Schirmes ein schwachleuchtender Fleck von dem Lichte A und ein hellerer von dem Lichte B.
Jetzt schiebt man, um beide Flecken in gleiche Lichtstärke zu versetzen, das Licht
B so weit zurück bis die geforderte Gleichheit der
Lichtintensitäten eingetreten ist. Dieses erkennt man an den Spiegelbildern der
Lichtflecke, wobei das Gesicht genau über dem Schirm D
zu halten und aus beide Spiegel zugleich zu richten ist. Die Durchsichtigkeit des
Glases aus B mißt man nun mit dem Quadrate der
Entfernung von dem Schirm D. Haben wir somit das Licht
B in eine Entfernung von 3 Theilstrichen von dem
Schirm bringen müssen, so ist die Durchsichtigkeit des geprüften Glases als 9 zu
betrachten, wenn wir die Durchsichtigkeit des Glases aus A, welches in der Distanz 1 als vergleichende Einheit dient, gleich 1
angenommen haben.
Ist zu untersuchen, wie diel das Glas von dem Gesammtlichte durchläßt, so beseitigen
wir die Scheibe auf A und setzen an ihre Stelle jene von B, während der Tubus von B
frei bleibt. Jede Lichtquelle in der Distanz 1 vom Schirm entfernt gibt einen
Lichtflecken, wovon jener des freien Lichtes stärker ist. Wir bestimmen die
Lichtintensität des totalen Lichtes im Vergleiche zu dem Lichtflecke von A dadurch, daß wir B
zurückschieben. Hat dabei B den Theilstrich 4 getroffen,
so ist die Intensität des Fleckens von B mit 16 und jene
von A mit 1 zu bezeichnen. Das Verhältniß der
Lichtintensitäten ist also hier mit 1/16 ausgedrückt.
Es fragt sich nun, mit welcher Zahl ist die Lichtintensität des Fleckens bei A zu bezeichnen, wenn wir jene des totalen Lichtes mit
100 ausdrücken? Dieß ergibt sich aus dem Quotienten 100/16 = 6,25.
Die Ergänzungszahl zu 100, nämlich 100-6,25 = 93,75 bezeichnet uns das nicht
durchgelassene Licht. Es wäre somit das geprüfte Glas ein 6,25 procentiges zu nennen
in Bezug aus die durchdringende Lichtmenge, während es ein 93,75 procentiges zu nennen ist, wenn man die Dunkelheit des
Glases in Betracht zieht.
Die angegebene Messungsmethode gilt aber nur für den Fall, daß man Glassorten von
gleicher Dicke anwendet. Da bei einem praktischen Verfahren Absorptionscoefficienten
nicht in Rechnung gebracht werden können, indem dieß der Einfachheit bedeutenden
Eintrag thut, so muß man die Messung bei verschieden starken Glastafeln in folgender
Weise ausführen:
Wäre die zu prüfende Glasscheibe aus B
Fig. 20
dicker als jene auf A, so erhielte man mit Anwendung der
angegebenen Messung für die Durchsichtigkeit des Glases eine zu geringe Zahl. Es
müssen die Glasscheiben somit vor dem Versuche auf ihre Dicke gemessen werden. Zu
genaueren Ergebnissen brauchte man allerdings ein Sphärometer; in der Praxis wird
aber ein genauer Längenmaaßstab hinreichen, um die Stärke der Gläser auf einer gut
abgeschliffenen Stelle abzugreifen.
Nehmen wir an, es wäre die Scheibe aus B um 0,2 stärker
als jene auf A, so brauchen wir bloß die Lampe A um 0,2 der Längeneinheit am Maaßstabe zurückzuschieben
und dann wie früher fortzuschreiten. Im entgegengesetzten Falle, wenn die zu
prüfende Scheibe dünner ist, brauchen wir die Lichtquelle A nur um die gefundene Differenz aus dem Maaßstabe dem Schirme D zu nähern.
Die letztere Messungsmethode dürfte, da sich Gläser von gleicher Dicke selten
zusammenfinden, häufiger Anwendung finden.
In jenen Fällen, wo nur eine Lichtquelle möglich wäre, ist das Diaphanometer in der
Form, welche Fig.
21 zeigt, anzuwenden.
Der Winkelmaaßstab stellt uns hier den gebrochenen Längenmaaßstab C, C aus Fig. 20 vor. seine Arme
müssen in einem Gelenke beweglich seyn. Beim Versuche ist der Winkel des Maaßstabes
aus etwa 5° einzustellen. Die Lichtquelle A befindet
sich dann in dem Scheitel. Es ist gut wenn sie sammt dem Gestell und Fuß mit Hülfe
eines Stieles als Verlängerung des Ständers in einen Ring des Winkelmaaßstabes
(natürlich senkrecht auf die Winkelebene) aufgesetzt und außer dem Gebrauche wieder
herausgehoben werden kann. Der Cylinder hat die Form von Fig. 23 und 24 im
Grundriß. seine beiden Tuben entsprechen dem Winkel des Maaßstabes. An beiden Armen
des Maaßstabes ist ein Schirm B und C (Fig. 21) aus dünnem,
etwas durchsichtigem Milchglas. Beide sind verschiebbar. Dabei dient der Schirm B 1 von der Lichtquelle, während C die ganze Länge des zweiten Armes zu Gebote steht. Das Gesicht ist bei
dem Versuche entgegen den Tuben zu halten und die gleiche Intensität der beiden
Lichtflecke durch Verschieben des Schirmes C zu
erreichen. Dieses Instrument erfordert schon ein etwas geübteres Auge, denn hier
sind die beiden Lichtflecke entfernter von einander als bei dem ersten Instrumente,
daher ihre Vergleichung schwieriger ist. Das Verfahren ist dasselbe wie beim ersten
Instrument. Sollte man Glassorten in Beziehung auf das Sonnenlicht prüfen, so müssen
die beiden Arme des Winkelmaaßes parallel gestellt seyn und ebenso parallele Tuben
angewendet werden, welche entweder zu einem Heliostat passen oder im Fensterladen
angebracht werden können.
Dieses Diaphanometer dürfte für Glaser, Glashändler oder Optiker am ehesten geeignet
seyn.
Tafeln