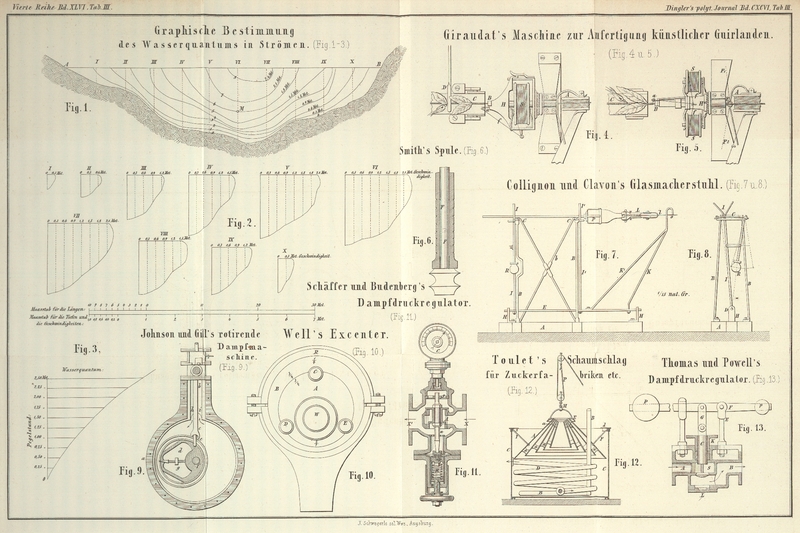
| Titel: | Graphische Bestimmung des Wasserquantums in Strömen; mitgetheilt von Eduard Schmitt, Ingenieur am k. k. polytechnischen Institute in Wien. |
| Autor: | Eduard Schmitt |
| Fundstelle: | Band 196, Jahrgang 1870, Nr. XXIII., S. 97 |
| Download: | XML |
XXIII.
Graphische Bestimmung des Wasserquantums in
Strömen; mitgetheilt von Eduard
Schmitt, Ingenieur am k. k. polytechnischen Institute in
Wien.
Mit Abbildungen auf Tab.
III.
Schmitt, über graphische Bestimmung des Wasserquantums in
Strömen.
Im vorigen Jahrgang dieses Journals, Bd. CXCIII S.
345, habe ich unter dem Titel: „Das Messen
des Wasserquantums in Strömen“ eine dem Journal of the Franklin Institute entnommene Methode zur
Bestimmung der Wassermenge zur Kenntniß gebracht, bei welcher man in der bekannten
Weise das Stromprofil in mehrere verticale Streifen theilt, im Schwerpunkte eines
jeden derselben die Geschwindigkeit mißt und deren Fläche mit der gemessenen
Geschwindigkeit multiplicirt. Die Summe dieser Producte gibt die durch das
betreffende Profil fließende Wassermenge an. Es wurde dann gezeigt, wie man mittelst
des sogenannten elektrischen hydrometrischen Flügels die
nothwendigen Geschwindigkeitsmessungen mit der erforderlichen Genauigkeit vornehmen
kann.
Anschließend an diesen Aufsatz erlaube ich mir im Vorliegenden ein graphisches Verfahren mitzutheilen, um das Wasserquantum in Strömen (oder Canälen) zu bestimmen, welches in sehr einfacher Weise zu einem
möglichst genauen Resultate führt. Dasselbe ist von Professor C. Culmann erfunden und versuchsweise auch an einzelnen
Messungen im Rheine angewendet worden.
Denken wir uns ein Stromprofil Fig. 1, in welchem die
horizontale Gerade AB den Wasserspiegel vorstellt.
Denken wir uns ferner in jedem Wasserfaden die Geschwindigkeit des Wassers, also den
Weg welchen der betreffende Wasserfaden in einer Secunde zurücklegt, normal zum
Stromprofile aufgetragen, so werden die Endpunkte sämmtlicher Normalen die
Oberfläche eines Körpers bestimmen, dessen Volumen uns das gesuchte Wasserquantum
vorstellt. Es wird sich somit nur darum handeln, ein einfaches Verfahren zu
ermitteln, den Rauminhalt dieses pro Secunde
vorgeschobenen Wasserkörpers aufzufinden.
Zu diesem Zwecke nehmen wir in dem von uns gewählten Stromprofile mehrere, am
vortheilhaftesten gleich weit von einander entfernte Punkte I, II, III, IV... X an.
In diesen einzelnen Punkten stellen wir nun in verschiedenen Tiefen mittelst eines
guten hydrometrischen Flügels möglichst genaue Geschwindigkeitsmessungen an. Von der
Anzahl der gewählten Punkte I, II, III, IV.... X, sowie auch von der Zahl der
vorgenommenen Geschwindigkeitsmessungen wird zum großen Theile die Genauigkeit des
Resultates abhängen.
Wir stellen uns nun, wie in Fig. 2, für die einzelnen
Punkte I, II, III, IV... X die gemessenen Geschwindigkeiten graphisch dar, indem wir
nämlich jedesmal von 0 aus vertical abwärts die Wassertiefen als Ordinaten,
horizontal nach rechts die Geschwindigkeiten als Abscissen auftragen. Jede Ordinate
mit der ihr zugehörigen Abscisse wird einen Punkt bestimmen, und wir können diese
Punkte durch continuirliche Curven verbinden. Diese Curven, von denen Humphreys und Abbot mit
einigem Unrecht behaupten, daß sie Theile einer Parabel seyen, werden sich dann wie
die in Fig. 2
verzeichneten darstellen. Durch die so erhaltenen Curven ist aber der oben erwähnte
pro Secunde vorgeschobene Wasserkörper bestimmt, wir
brauchen uns denselben nur als Umhüllung dieser krummen Linien zu denken. Wir können
aber die Oberfläche dieses Wasserkörpers noch anders fixiren. Es wird nämlich mit
Hülfe der in Fig.
2 verzeichneten Curven ein Leichtes seyn, im gewählten Stromprofile für
die verticalen Schnitte I, II, III, IV... X Punkte von gleicher Geschwindigkeit zu
finden. Diese Punkte lassen sich dann durch continuirliche krumme Linien so mit
einander verbinden, daß die Punkte einer jeden solchen Curve gleiche Geschwindigkeit
besitzen. Für das gewählte Stromprofil wurden die in Fig. 1 dargestellten
Curven 1, 2, 3, 4,..., 8 aufgefunden, entsprechend den Geschwindigkeiten von 0,3
Met., 0,6 Met., 0,9 Met., 1,2 Met.... 2,4 Met. Um z.B. den Punkt M der Curve 6 zu bestimmen, brauchten wir nur in Fig. 2, VI von
0 aus nach rechts die Geschwindigkeit von 1,8 Met. als Abscisse aufzutragen; die
entsprechende Ordinate gab natürlich die Tiefe des Punktes M unter dem Wasserspiegel, somit die Lage desselben an.
Wir dürfen uns nun diese Curven nicht in der Ebene des Stromprofiles vorstellen,
sondern müssen uns dieselben auf der Oberfläche des bereits mehrfach gedachten, pro Secunde vorgeschobenen Wasserkörpers verzeichnet
denken. Diese krummen Linien haben nun immer einen gleichen Horizontalabstand oder
eine Aequidistanz a = 0,3 Met., und wir können die im
Stromprofile Fig.
1 verzeichneten Curven als die Projectionen der auf der Körperoberfläche
verzeichneten krummen Linien betrachten. Diese in Fig. 1 erhaltenen Curven
sind ebenso aufzufassen wie die Schichtenlinien einer Terrainkarte. Ebenso wie durch
diese bei bekannter Aequidistanz die Konfiguration des Termins vollständig gegeben
erscheint, ebenso ist auch in unserem Beispiele durch die zuletzt erhaltenen Curven
der pro Secunde vorgeschobene Wasserkörper vollkommen
bestimmt.
Um nun das Volumen desselben zu berechnen, ziehen wir immer den zwischen je zwei
Curven gelegenen Körper in Betracht. Nehmen wir zunächst den durch die
Profilumfangslinie 0 und die Curve 1 begrenzten Körper an, und nennen wir die von
diesen Curven eingeschlossenen Flächen beziehungsweise f₀ und f₁, so wird das Volumen v₁ des von ihnen eingegrenzten Körpergürtels sehr
nahe
v₁ = (f₀ + f₁)/2 . a
seyn. Ist die von der Curve 2 beschriebene Fläche f₂, so beträgt der Rauminhalt der Körperzone
zwischen Curve 1 und 2
v₂ = (f₁ + f₂)/2 . a
ebenso für den zwischen Kurven 2 und 3 eingeschlossenen
Körper
v₃ = (f₂ + f₃)/2 . a
. . . . . . . . . . . . .
endlich wird das Volumen des zwischen der vorletzten Curve n–1 und der letzten n
gelegenen Körpertheiles
vn= (fn–1 + fn)/2 . a
betragen. Das Gesammtvolumen des pro Secunde vorgeschobenen Wasserkörpers oder das Wasserquantum ist
somit
Q = v₁ + v₂ + v₃ + . .
. . + vn
oder
Q = a (f₀/2 + fn/2
+ f₁ + f₂ +
f₃ . . . . fn–1); d.h.
man addire sämmtliche von den Curven 0, 1, 2, 3,....n eingeschlossenen Flächen, subtrahire davon die halbe
Summe der von der ersten und der von der letzten Curve umschriebenen Flächen und
multiplicire die Differenz mit der Aequidistanz.
Die Flächen f₀, f₁, f₂ ,...
fn kann man nun vermittelst der Simpson'schen Regel oder sonst eines geometrischen
Verfahrens berechnen oder vortheilhafter mittelst eines Planimeters auffinden. Im
letzteren Falle gestaltet sich die Operation besonders einfach, weil das Planimeter die Addition
der einzelnen Flächen selbst vornimmt. Das Verfahren ist dann nämlich ganz einfach
folgendes: Man stellt den Stift des Planimeters auf einen Punkt der ersten Curve (0)
auf, macht die Ablesung und umfährt dieselbe. Nun liest man wieder ab, notirt die
umschriebene Fläche (f₀) und umfährt nun der
Reihe nach die folgenden Curven (1, 3, 3...) mit dem Stifte des Planimeters; erst
wenn man die vorletzte (n–1) umschrieben hat,
macht man wieder eine Ablesung, umfährt endlich auch die letzte (n) und liest abermals ab. Die Differenz zwischen der
nach Umschreibung der letzten und der nach Umfahrung der vorletzten Curve
abgelesenen Zahl gibt die Fläche (fn) an, welche von der letzten Curve eingeschlossen
ist. Subtrahirt man von der Schlußablesung die zu Beginn gemachte, so gibt die
Differenz die Summe der von sämmtlichen Curven (0, 1, 2, 3,.... n–1, n) begrenzten Flächen (f₀ + f₁ + f₂ + f₃ + . .
. . . + fn–1 +
fn). Zieht man
hiervon die halbe Summe der von der ersten und letzten Curve eingeschlossenen
Flächen ((f₀ + fn)/2) ab, und multiplicirt die Differenz mit der
Aequidistanz a, so gibt das Product das Wasserquantum
(Q).
In unserem gewählten Beispiele betrug die Ablesung des Planimeters bei Einstellung
des Stiftes auf der Curve 0... 79,86, nach Umfahrung dieser Curve 84,48. Hierauf
wurden fortlaufend die Curven 1, 2, 3, 4, 5, 6 + 7 mit dem Stifte umschrieben, die
nunmehrige Ablesung des Planimeters mit 100,46 notirt, weiters die letzte Curve 8
mit dem Stifte umfahren und schließlich 100,76 abgelesen. Offenbar ist nun die
Fläche f₀ = 84,48 – 79,86 = 4,62 und fn = 100,76 –
100,46 = 0,30; die Summe der von sämmtlichen Curven eingeschlossenen Flächen f₀ + f₁ + f₂ + f₃ + f₄ + f₅ + f₆ + f₇ + f₈ = 100,76 – 79,86 = 20,90; somit das
gesuchte Wasserquantum, da a = 30 Centimeter ist,
30 [20,90 – (0,30 + 4,62)/2] = 553,20
An unserem Instrumente ist jede Fläche noch mit 6 zu multipliciren, so daß
dasselbe
6 . 553,20 = 3319,20 Quadratcentimet. = 0,33192 Quadratmeter
absoluten Flächenmaaßes ergibt.
Die Längen des in Fig. 1 gezeichneten Stromprofiles sind in 1/35 und die Tiefen in 1/7
aufgetragen, somit ist das wirkliche Wasserquantum
Q = 35 . 7 . 0,33192 = 81,3204 Kub. Met.
Dieses höchst einfache Verfahren der Aufsuchung des Wasserquantums in irgend einem Stromprofile
gestattet aber auch, in möglichst genauer Weise die mittlere Geschwindigkeit v zu bestimmen. Ist nämlich die Fläche des Stromprofiles
F, so ist bekanntlich
v = Q/F.
Es ist aber ferner auch bekannt, daß in den für die Berechnung der mittleren
Geschwindigkeit gebräuchlichen Formeln immer gewisse constante Größen, gewisse
Erfahrungscoefficienten vorkommen. Mit Hülfe dieser directen Bestimmung der
Wassermenge und der daraus bestimmten mittleren Geschwindigkeit lassen sich nun
diese Coefficienten sehr leicht auffinden.
Hierdurch wird es aber möglich, aus der Bestimmung des Wasserquantums für ein
bestimmtes Stromprofil und einen bestimmten Wasserstand, das Wasserquantum dieses
Profiles auch bei beliebigen anderen Wasserständen zu berechnen. Hat man nämlich für
ein gewisses Flußprofil bei irgend einem Pegelstande die Wassermenge bestimmt, so
kann man aus derselben die mittlere Geschwindigkeit berechnen. Kennt man diese, so
kann man den Erfahrungscoefficient der Formel für die mittlere Geschwindigkeit
bestimmen und dann, ohne jede weitere Messung im Flusse, das Wasserquantum für
andere Pegelstände berechnen. Trägt man nun (Fig. 3) die Pegelstände
als Ordinaten, die ihnen entsprechenden Wassermengen als Abscissen auf, so bestimmen
die Endpunkte der letzteren eine Curve. Diese liefert dann ein ganz einfaches
Mittel, um für ein Stromprofil bei irgend einem Pegelstande sofort das Wasserquantum
daraus entnehmen zu können.
Tafeln