| Titel: | Die mehrkurbelige Cincylinder-Pumpe; von H. Haedicke, königl. Marine-Ingenieur in Kiel. |
| Autor: | H. Haedicke |
| Fundstelle: | Band 197, Jahrgang 1870, Nr. XXI., S. 97 |
| Download: | XML |
XXI.
Die mehrkurbelige Cincylinder-Pumpe; von
H. Haedicke, königl. Marine-Ingenieur in
Kiel.
Mit Abbildungen auf Tab.
III.
Haedicke, über die mehrkurbelige
Cincylinder-Pumpe.
An Bord der englischen Dampfschiffe und, wohl durch dieselben herübergebracht, auch
bei den unserigen, findet man vielfach eine Pumpe mit mehreren Kolben in einem
Cylinder, deren Kolbenstangen, meist excentrisch aufgesetzt, durch eine quer über
dem sich oben ansatzförmig erweiternden Cylinder liegende Welle getrieben werden.
Diese Welle enthält entweder eine entsprechende Anzahl Kröpfungen oder aber
Excenter, oft Dreiecks-Excenter, welche die mit einem Rahmen endenden
Kolbenstangen bewegen.
Es führen diese Pumpen den Namen: Downton-Pumpen.
Sie sind meist mit drei, zuweilen auch mit zwei Kolben construirt und haben
demzufolge eine eigenthümliche Wirkungsweise, welche wir nunmehr näher betrachten
wollen.
Die beispielsweis in der Anzahl von 3 angenommenen Kolben, welche sich untereinander
mit einem absoluten Hub gleich dem der Kurbel in dem Pumpencylinder bewegen, sind
mit nach oben sich öffnenden Ventilen versehen. Hat nun noch die Pumpe ein
besonderes Bodenventil, so wird der unterste Kolben mit diesem das gewöhnliche Spiel
der einfach wirkenden Pumpe haben. Der nächst nach oben folgende Kolben hingegen
wird sich je nach den Kurbelstellungen von dem unteren entfernen, resp. sich ihm
nähern, und ebenso wird es mit dem obersten Kolben zum mittleren stehen. Es wird je
der unterste zweier aufeinander folgenden Kolben als Bodenventil für den oberen
dienen.
Um nun der Wirkungsweise dieser Kolben theoretisch näher zu kommen, wollen wir
zunächst die Entfernungen derselben vom Mittelpunkt der Welle für eine beliebige
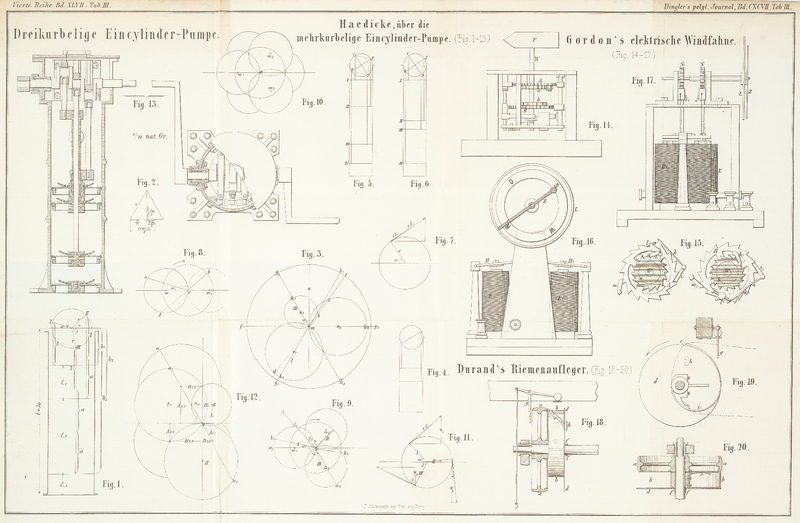
Stellung der letzteren, welche wir durch den Winkel ω (s. Fig. 1), auf die Kurbel
I bezogen, markiren wollen, bestimmen, und dabei von
der Voraussetzung ausgehen, die Bewegung geschehe durch 3 gleichmäßig vertheilte
Kurbelzapfen (I, II, III).
Es seyen die unter sich gleichen Radien der Kurbeln = r,
ihre Winkel mit der Horizontalen beziehungsweise = ω,
α, β. Die Länge der Kolbenstange zu I sey = l, die der zu II gehörigen sey um a, die zu III um 2 a größer,
also resp. = 1 + a und 1 + 2 a. Die Entfernung endlich des Bodenventiles von der Wellenmitte sey = 1 +
3 a.
Bezeichnen wir nun die Entfernungen der 3 Kolben von der Achse resp. mit b₁, b₂, b₃ , dann ist
offenbar:
für I: b₁ = l – r sin ω
für II: b₂ = l + a – r sin α
für
III: b₃ = l + 2
a + r sin β.
Die Größen α und β lassen sich leicht durch ω
ausdrücken. Man denke sich die Kurbel I rückwärts verlängert, dann wird der Winkel
II, III = 120°, halbirt und es ergibt sich direct:
α = 60 – ω
β = 60 + ω.
Mithin wird:
b₁ = l – r sin ω
b₂ = l + a – r sin 60 cos ω + r cos 60 sin ω
b₃ = l + 2 a + r sin 60 cos ω + r cos 60 sin ω
Bezeichnen wir nun
sin 60 = n . cos 60 = m
dann wird:
b₁ = l
– r sin ω
b₂ = l + a – rn
cos ω + r . m sin ω
b₃ = l + 2 a + rn
cos ω + rm
sin ω
Führen wir nun noch die in der Fig. 1 angegebenen
Bezeichnungen für die Kolbenabstände von einander resp. vom Bodenventil, ξ₁, ξ₂, ξ₃, ein, so
erhalten wir:
ξ₁ = b₂ – b₁; ξ₂ = b₃ – b₂; ξ₃ = l + 3 a – b₃
Mithin wird:
ξ₁ = a
– rn
cos ω + r (m + 1) sin ω
ξ₂ = a + 2 rn
cos ω
ξ₃ = a
– rn
cos ω – rm
sin ω
Und diese Gleichungen können wir auch schreiben:
ξ₁ = a
– (rn
cos ω – r (m + 1) sin ω)
ξ₂ = a
– (– 2 rn
cos ω 0 . sin
ω)
ξ₃ = – (rn
cos ω + rm
sin ω).
Bezeichnen nun A und B die
rechtwinkeligen Coordinaten des Mittelpunktes eines Kreises, bezogen auf einen Punkt der
Peripherie desselben, so lautet die Polargleichung für diesen Kreis:
ρ = 2 A
sin ω + 2 B cos ω
Wenn A die Ordinate, B die
Abscisse des Mittelpunktes darstellt.
Es lassen sich mithin die in der Klammer befindlichen Größen der für ξ gefundenen Ausdrücke als Radien vectoren von
Kreisen einführen, deren Mittelpunkts-Coordinaten bezüglich gleich den halben
Factoren der trigonometrischen Functionen sind.Textabbildung Bd. 197, S. 99Aus der nebenstehenden Figur, in welcher A
die Ordinate, B die Abscisse des
Kreismittelpunktes o bedeuten, ergibt sich
durch Projection dieser Größen auf den halben Radius vector am = β/2 direct : β/2 =
A sin ω + B cos ω.Man s. übrigens: Zeuner, Schiebersteuerungen,
wo diese Darstellungsmethode in sehr schöner Weise für die
complicirtesten Bewegungen durchgeführt ist.
Bezeichnen wir nunmehr diese Koordinaten mit A und B, versehen mit den entsprechenden Indices, so ergibt
sich:
ξ₁ : A͵= r(m + 1)/2
B₁ = (r .
n)/2
ξ₂ : A͵͵
= 0
B₂ = – r . n
ξ₃ : A͵͵͵ =
(r . n)/2
B₃ = (r .
m)/2
Da nun n = sin 60, m = cos 60, so lassen sich
die Größen A und B leicht
durch ein gleichseitiges Dreieck, dessen Seite = r ist,
constructiv finden (s. Fig. 2).
Trägt man nunmehr die so gefundenen Coordinaten auf, und schlägt die dazu gehörigen
Kreise, so erhält man die Fig. 3.
Es sind hier die 3 Mittelpunkte, 01, 02 und 03 durch die oben angegebenen Coordinaten
bestimmt, und das Ganze mit einem Kreise von dem Radius = a umgeben.
Jeder Radius vector, welcher in dieser Figur gezogen ist, gibt also in seinem durch
die Kreise I, II und III begrenzten Stück die in der Klammer für den Ausdruck ξ stehende Größe. Dieselbe von a, dem Radius des größten Kreises, abgezogen ergibt ξ selbst.
Bildet also die Kurbel I den Winkel fme = ω mit der Abscissen-Achse, so ist:
ξ₁ = a – (– md) = de
ξ₂ = a – mc = ce
ξ₃ = a – mb = be.
Um diese Stücke (ξ1,
ξ₂, ξ₃) stehen also die Kolben von einander resp. vom Bodenventil
entfernt, wenn die Kurbel I sich von ihrer Anfangsstellung aus um den Winkel ω gedreht hat.
Beachtet man die Ab- und Zunahme dieser Werthe für ξ bei fortschreitender Drehung, so findet man die Maxima und Minima
in denjenigen Stellungen der Kurbel I, wo der Mittelpunkt eines der Kreise getroffen
wird.
So wird ξ₁ ein Maximum in der Länge h₁, k₁ für
ein Minimum in h₁, g₁ für
Aehnlich wird ξ₂ ein Maximum für ω = 0 in fh₂, ein Minimum für ω = 180°
in h₂g₂. Und
endlich hat ξ₃ ein Maximum in h₃ k₃ für ω = fmk₃, ein Minimum in h₃ g₃ für ω = fmg₃.
Aus diesen Größen erhalten wir nun offenbar die relativen Kolbenhube, d.h. die Länge,
um welche die Kolben zu einander spielen, oder, wenn wir auf die Wirkung dieses
Spieles als Saugen und Pressen zurückgehen, die Höhe der bei einer Umdrehung
zwischen je 2 Kolben aufgenommenen und von ihnen abgegebenen Wassersäule, indem wir
das Minimum von dem Maximum subtrahiren.
Bezeichnen wir die Durchmesser der Kreise I, II und III beziehungsweise mit D₁, D₂, D₃, so ergibt sich für I der relative Hub H₁ als mk₁+
mh₁ – (mg₁ – mh₁) = a + D₁ – (a – D₁) = 2
D₁. Analog erhalten wir für den Hub des
Kolbens II zu III: H₂ = 2 D₂, und ebenso: H₃ = 2 D₃.
Diese Durchmesser lassen sich aber leicht aus den oben gefundenen
Mittelpunkts-Coordinaten berechnen.
Es ist offenbar:
Textabbildung Bd. 197, S. 100
Da nun m = cos 60 = 0,5, n = sin 60 =0,866 ist, so
wird
D₁ = r √3
D₂ = 2 r
sin 60
D₃ = r
Und hieraus folgt für die relativen Kolbenhube:
Textabbildung Bd. 197, S. 101
Wir erhalten also als Gesammthub die Größe:
H = 8,928 . r
Diese Betrachtung zeigt zunächst, daß die relativen Hube der 3 Kolben zu einander
gleich sind der doppelten Entfernung der treibenden Warzen (= 2 . 2 r . sin 60), und daß, wie
ohne Weiteres zu ersehen war, der untere Kolben zum Bodenventil die gewöhnliche
Wirkung, den Hub = 2 r hat.
Würden die drei Kolben einfach-wirkend, jeder in einem besonderen Cylinder
laufen, so würde die Summe der wirksamen Hube bei einer Umdrehung offenbar = H₁ = 6 r betragen.
Es liefert also die vorliegende Pumpe 8,928/6 = 1,488 mal so viel Wasser, als eine
3cylindrige Pumpe von sonst gleichen Dimensionen.
Das so eben über den relativen Hub zweier Kolben gefundene Gesetz läßt sich ohne
Weiteres auf andere Fälle ausdehnen. Nimmt man z. B.
eine eincylindrige Pumpe mit 2 einander gegenüberstehenden Kurbeln (Fig. 4), so würden die
beiden Kolben miteinander den relativen Hub = der doppelten Entfernung ihrer Warzen
= 4 r, der untere mit dem Bodenventil den Hub = 2 r, haben. Mithin würde sich hier der Gesammthub auf 6
r berechnen. Eine 2cylindrige
einfach-wirkende Pumpe würde unter sonst gleichen Umständen einen Hub = 4 r liefern, so daß sich hier das Verhältniß der
Leistungsfähigkeiten auf das 1 1/2 fache stellt.
Bei der 4kurbeligen Pumpe können wir zwei Variationen machen.
Verbindet man die aufeinanderfolgenden Kolben mit den in der Bewegungsrichtung
aufeinanderfolgenden Kurbeln, dann ist die Entfernung der Warzen für die Berechnung
des relativen Hubes offenbar (= 1 – 2, Fig. 5) = r √2 = 1,415 . r.
Bezeichnen wir also wieder die aufeinanderfolgenden (von oben nach unten) relativen
Hube mit H₁...
H₄, dann wird:
H₁ = 2,83 r
H₂ = 2,83 r
H₃ = 2,83 r
H₄ = 2 r
–––––––––––
H = 10,49 r
Wir erhallen mithin als Gesammthub H = 10,49. r.
Verbinden wir aber je zwei diametral stehende Kurbelzapfen mit den aufeinander
folgenden Kolben (Fig. 6), so erhalten wir:
H₁ = 4 r
H₂ = 2,83 r
H₃ = 4 r
H₄ = 2 r
–––––––––––
H = 12,83 r
Da die Entfernung der Warzen für die Kolben I und II = 2 r, die für II und III = r√2, die für
III und IV wieder = 2 r wird. Es beträgt mithin in
diesem Falle der Gesammthub: H = 12,83 r.
Bei einer 4stiefeligen Pumpe von denselben Verhältnissen (oder einer 2stiefeligen,
doppelt-wirkenden) würde der Gesammthub = 8 r
betragen, und es ergibt sich daher das Verhältniß der Leistungsfähigkeit der
4kurbeligen Eincylinderpumpe zu der 4fachen einfach-wirkenden:
a) Bei aufeinander folgender Verbindung der Kolben mit
den Kurbeln zu 10,49/8 = 1,31;
b) bei theilweis diametraler Verbindung zu 12,83/8 =
1,6.
Es ist also die letztere Verbindungsart die vortheilhaftere; denn sie liefert bei
denselben Materialien eine kräftigere Wirkung.
Man ersieht hieraus, daß die vortheilhaftesten Verbindungen bei gegebenen
Kurbelzahlen diejenigen sind, bei denen die größten Warzenentfernungen für je 2
aufeinander folgende Kolben entstehen.
Die Kurbel-Anzahl noch weiter zu treiben, hat kein praktisches Interesse; denn
schon bei 4 Kurbeln stößt man, wenigstens bei den bisher gebräuchlichen
Constructionen mit excentrischen Kolbenbefestigungen, auf wesentliche
Schwierigkeiten. Interessant aber wird noch der Fall, wo 6 Kurbeln angewendet
werden. Verbindet man hier in der Reihenfolge 1, 2, 3, 4, 5, 6, so erhält man wieder
für die relativen Kolbenhube die doppelte Entfernung der Warzen, also je gleich 2
r. Es gibt also eine so eingerichtete
Eincylinder-Pumpe dasselbe Resultat wie eine 6 fache einfach-wirkende oder
eine 3fache doppelt-wirkende Pumpe gewöhnlicher Construction, nämlich H = 12 r.
Verbindet man aber so, daß man möglichst oft als treibende Warzen-Entfernung
den Durchmesser erhält, also: 1–4, 4–2, 2–5, 5–3, 3
–6, so resultiren die Zahlen: 4 r, 4 r sin 60, 4 r, 4 r sin 60, 4 r und 2 r, und man erhält als Gesammthub 20,928 r, mithin das 1,744fache.
Diese Betrachtung der verschiedenen Wirkungsweise ein und derselben mehrfachen
Kurbelwelle bei verschiedenen Kolbenverbindungen ist zu gleicher Zeit geeignet, die
Zweifel zu beseitigen, welche bei einer gewissen „praktischen
Anschauungsweise leicht entstehen können über die Richtigkeit der angenommenen
Thätigkeit dieser Art Pumpen.
Denn es liegt offenbar der Gedanke nicht fern, zu calculiren:
Jeder Kolben hat seinen Hub = 2 r, muß also dem
entsprechend Wasser liefern. Also gibt eine n kurbelige
Pumpe 2 nr als Gesammthub. Daß diese freilich nahe
liegende Betrachtungsweise eine irrige seyn muß, geht schon bei der Annahme zweier
immer in gleichen Abständen von einander in ein und demselben Cylinder laufenden
Ventilkolben hervor. Hier wirkt offenbar der zweite Kolben nur als vermehrte
Sicherheit gegen Abfluß durch Undichtheiten und zur Vermehrung der
Kolbenreibung.
Von dem bisherigen Gesichtspunkte aus würde also die mehrkurbelige Eincylinderpumpe
zwischen den einfach- und doppelt-wirkenden Pumpen gewöhnlicher
Construction mit gleicher Kurbelzahl stehen. Denn es liefert bei 2 Kurbeln:
die doppelte einfach-wirkende Pumpe: 4 r
die doppelte doppeltwirkende Pumpe: 8 r
die Downton-Pumpe: 6 r
bei 3 Kurbeln:
die dreifache einfach-wirkende Pumpe: 6 r
die dreifache doppelt-wirkende Pumpe: 12 r
die Downton-Pumpe = 8,928 r
Dabei ist die absolute Kolbenreibung bei der einfach-wirkenden Pumpe dieselbe
wie bei der doppelt-wirkenden und der Downton-Pumpe; mithin stellt sich die relative Kolbenreibung am
günstigsten bei der doppelt-wirkenden vielfachen Pumpe, am ungünstigsten bei
der einfachwirkenden vervielfachten, so daß auch hier die Downton-Pumpe die Mitte einnimmt.
Beachtet man aber die bei der doppelt-wirkenden Pumpe nothwendige Verdoppelung
der Anzahl der Ventile, so ergibt sich da, wo es auf eine einfache, raumersparende
Aufstellung ankommt, ein Vortheil für das Downton-System.
Freilich geschieht dieß nun wieder auf Kosten der Revisionsfähigkeit. Während bei
den gewöhnlichen Systemen entsprechender Construction einfach ein Ventildeckel
aufzunehmen ist, müssen hier in diesem Falle sämmtliche Kolben herausgehoben und
nachgesehen werden. Ein fernerer Punkt von nicht unwesentlicher Bedeutung ist die
Geschwindigkeit des ausströmenden Wassers, also die eventuelle Nothwendigkeit der
Anbringung von Windkesseln.Bekanntlich hat der Windkessel den Zweck, die Geschwindigkeit des Wassers in
den Momenten annähernd zu erhalten, wo der Kolben und also auch das ihm
folgende Wasser die Geschwindigkeit = 0 hat. Bei schnell gehenden Pumpen und
solchen mit langen (Saug- oder Druck-) Leitungen ist die bei
jedem wirksamen Hub dem Wasser zu ertheilende lebendige Kraft, wenn dasselbe
auf die Geschwindigkeit = 0 jedesmal kommen kann, oft so bedeutend, daß
harte, sogar gefahrbringende Schläge und Stöße entstehen. Der Windkessel, am
Saugrohr sowohl wie am Druckrohr, beseitigt diese, indem er die
Geschwindigkeitsänderungen aufhebt oder doch wenigstens stark vermindert. Es
ist daher nicht nur bei Spritzpumpen, sondern auch bei langen Leitungen und
großen Wasser-Geschwindigkeiten die Anbringung eines Windkessels auch
am Saugrohr zu empfehlen.
Wir knüpfen daher hieran eine kurze Betrachtung über die Geschwindigkeit des
überhaupt von den Pumpen getriebenen Wassers, und werden dann im Stande seyn, auch
hierin ein Urtheil über die vorliegende Pumpe zu fällen.
Bezeichnen wir die als constant angenommene Winkel-Geschwindigkeit der Welle
mit ε, dann ist bei einem Winkel ω der Kurbel mit der zur
Bewegungs-Richtung des Kolbens senkrechten Linie die Kolbengeschwindigkeit
v = r . ε cos ω (s. Fig. 7); oder, um wieder
die Radien vectoren eines Kreises einsetzen zu können:
v = r .
ε cos ω + 0 . sin ω.
d.h. die Kolbengeschwindigkeiten für verschiedene
Kurbelstellungen lassen sich ausdrücken durch die Radien vectoren eines Kreises,
dessen Coordinaten: A = 0, B
= (r . ε)/2 sind.
Wir würden also von dem Mittelpunkt des Kurbelkreises (0) aus die Größe (r . ε)/2 positiv,
also unserer bisherigen Annahme gemäß nach links abtragen = 0 m, und mit 0 m als Radius um m einen Kreis schlagen (Fig. 8). Ist also 0 m = rε/2, dann wird
für die Kurbelstellung ω die Größe a 0 die Kolbengeschwindigkeit angeben.
Wir wollen nun und für die Folge annehmen, daß für die betrachteten Wassertheile der
Querschnitt des leitenden Rohres sich gleich bleibe, die Geschwindigkeit derselben
also stets proportional der treibenden Kolbengeschwindigkeit sey. Haben wir es nur mit einer
einfach-wirkenden Pumpe zu thun, dann wird von ω = – 90° bis ω =
+ 90 der Radius vector selbst die Wassergeschwindigkeit (oder eine derselben
proportionale Größe), für ω = 90 bis ω = – 90 aber seine Verlängerung die
Kolbengeschwindigkeit angeben, während die Wassergeschwindigkeit dieser Periode = 0
bleibt.
Für einfach-wirkende Pumpen gibt also nur der positive Theil des Radius vector
ein Maaß für die Wassergeschwindigkeit ab.
Bei doppelt-wirkenden Pumpen ist für den einen Hub der positive, für den
anderen Hub der negative Theil (die Verlängerung) maßgebend.
Für den Winkel der Kurbel = m 0 b würde also bei einer einfach-wirkenden Pumpe 0 α die rückgehende Kolbengeschwindigkeit seyn,
während die Wassergeschwindigkeit = 0 ist; für die doppelt-wirkende Pumpe
hingegen ist 0 α eine der Wassergeschwindigkeit
proportionale Größe.
Dieselbe Figur könnte man bei der Geschwindigkeit-Darstellung zweier einfach
wirkenden Pumpen mit diametral stehenden Kurbeln anwenden. Genauer oder vielmehr
logischer verfährt man, wenn man für die zweite Kurbel den diametral
gegenüberliegenden Kreis um m₁ mit dem Radius
(ε . r)/2 schlägt. Es gibt dann die positive
Länge des Radius vector für die immer durch dieselbe Kurbel angegebene Stellung die
Wassergeschwindigkeit, die Verlängerung desselben nach rückwärts die rückgehende
Geschwindigkeit des unteren Kolbens an.
Bildet nun (s. Fig.
9) ein Radius II in der Richtung der Rotation einen Winkel α mit dem Radius I, so muß der Durchmesser des
Geschwindigkeitskreises für den mit der Kurbel II verbundenen Kolben, – wenn
der die Geschwindigkeit durch seine positive Länge angebende Radius vector für
diesen Kolben derselbe seyn soll, wie für den Kolben I – um diesen Winkel α zurückstehen.
Ist dann z. B. ω = – α, so liegt die Kurbel II horizontal, hat also die größte
Kolbengeschwindigkeit im Gefolge. Der bezeichnende Radius vector steht dann aber um
α zurück, fällt mit dem Durchmesser 0 a₂ des zweiten Geschwindigkeitskreises zusammen,
gibt also auch die größte Kolbengeschwindigkeit (ε
r) an. Ist nun noch eine dritte Kurbel vorhanden, welche den Winkel 2 α mit der ersten bildet, so wird der Durchmesser
des dritten Geschwindigkeitskreises um 2 α
zurückstehen etc.
Ist dieser Winkel α = 120°, so werden die 3
Kurbeln gleichmäßig vertheilt seyn. Es werden dann ebenfalls die
Geschwindigkeitskreise (mit den Mittelpunkten m₁,
m₂, m₃)
gleichförmig vertheilt seyn, aber in entgegengesetzter Richtung auf einander
folgen.
Für einen beliebigen Winkel ω der Kurbel I werden
wir nunmehr folgende einzelne Kolbengeschwindigkeiten v
erhalten:
Für den Kolben I: v₁ = 0 b₁; die Wassergeschwindigkeit ist dieser Größe proportional.
Für den Kolben II: v₂ = 0 b₂, nach unten gehend, also Wassergeschwindigkeit = 0.
Für den Kolben III: v₃ = 0 b₃, Wassergeschwindigkeit ebenfalls = 0.
Für ω = a₁ 0
β₁ würde die Wassergeschwindigkeit
gleich zweien Kolbengeschwindigkeiten entsprechen müssen, nämlich von Seiten der
Kurbel I der Geschwindigkeit 0 β₁, von
Seiten der Kurbel II der Geschwindigkeit 0 β₂.
Als treibende Kolbengeschwindigkeit würde also in dieser Stellung 0 β₁ + 0 β₃ = 0 β anzusehen
seyn.
Construirt man also für die durch die Deckung der Kreise um m₁, m₂ und m₃ entstehenden Schleifen, Curven, deren Radien
vectoren gleich der Summe der einzelnen zu den genannten Kreisen gehörenden sind, so
geben diese drei Curvenstücke in Verbindung mit den dazwischen liegenden
Kreisbogenstücken eine zusammengesetzte Geschwindigkeit-Curve für das Wasser
einer 3kurbeligen einfach-wirkenden zusammengesetzten Pumpe ab, Fig. 10. (Die
eingesetzten Curvenstücke sind nachweisbar Kreise aus den Schnittpunkten der ersten
Kreise mit dem Radius derselben.)
Eine so construirte Pumpe wird also eine annähernd gleichmäßige Wassergeschwindigkeit
mit 6 nur geringen, aber gleichen Stößen haben. Niemals aber wird die
Wassergeschwindigkeit, wie bei der einkurbeligen einfach- und der
doppelt-wirkenden, sowie bei der 2kurbelig zusammengesetzten
einfach-wirkenden Pumpe = 0 werden können.
Bei der 2kurbeligen doppelt-wirkenden Pumpe würden wir vier Kreise mit resp.
senkrecht auf einander stehenden Durchmessern erhalten, deren Ecken ähnlich durch
Kreisbögen ausgefüllt werden, also eine Wassergeschwindigkeit mit 8 leichten Stößen
angeben würden.
Gehen wir mit der nunmehr gewonnenen Erfahrung zur Downton-Pumpe über, so erhalten wir Folgendes (Fig. 11): Unter Annahme
der bisherigen Bezeichnung ist:
v₁ = r . ε cos ω: v₂ = r . ε cos α =
r . ε . cos (60 – ω);
v₃ = r
ε cos β = r ε cos (120 – ω)
Oder: die Geschwindigkeit des Kolbens I zu II ist
V₁ = r . ε (cos
(60 – ω) + cos
ω)
die des Kolbens II und III:
V₂ = r
ε (cos (60 – ω) + cos (120
– ω))
und die des Kolbens III zum Boden (= v₃)
V₃ = r
ε cos (120 – ω)
dieß ausgeführt, gibt wieder:
V₁ = r . ε cos a (m + 1) + rεn sin ω
V₂ = – 2 rεn sin ω
V₃ = – rεm cos ω + rεn sin ω
Wir können also auch hier die Kolbengeschwindigkeit durch die Radien vectoren von
Kreisen ausdrücken, deren Mittelpunkts-Coordinaten bezugsweise sind:
Textabbildung Bd. 197, S. 107
Wir erhalten somit für die relativen Kolbengeschwindigkeiten dieselben Kreise, wie
für die subtractiven Größen in dem Ausdruck für die relativen Kolbenhube; es haben
jedoch diese Kreise eine andere Lage (Fig. 12). Bildet daher
die Kurbel I den Winkel ω mit der Horizontalen
(die Pumpenachse immer, wie bisher, senkrecht gedacht), so gibt 0 a₁ die Geschwindigkeit des Kolbens I zu II, 0 a₂ die von II zu III und 0 a₃ die von III an. Da jedoch die treibende Geschwindigkeit nur von
dem positiven Theil des Radius vector angegeben wird, so würden nur 0 a₁ und 0 a₃
als solche in Rechnung zu ziehen seyn. – Die Summe beider gibt 0 a. Wir haben also auch hier die Curven in der Art zu
vervollständigen, daß wir an den Stellen, wo der Radius vector durch eine Schleife
geht, denselben als Summe der beiden einzelnen Radien vectoren darstellen.
Die auf diese Weise entstehenden Zwischenstücke sind auch hier Kreise. Denn wir
erhalten:
V₁ + V₂ = r ε (m + 1) cos ω – r ε n sin ω
V₂ + V₃ = – r ε m cos ω
– r ε n sin ω
V₃ + V₁ = r ε cos ω + 2 r ε n sin ω
Mithin für die Mittelpunkts-Coordinaten:
Textabbildung Bd. 197, S. 107
Es entsteht so eine ganz eigenthümlich zusammengesetzte Curve, welche nunmehr ein
deutliches Bild von der Wassergeschwindigkeit für jede einzelne Stellung der Kurbel
I abgibt. Diese zeigt 6 Pulsschläge, welche während der einen Hälfte einer Umdrehung
stärker seyn werden, wie auf der anderen Hälfte.
Die Maximal-Geschwindigkeit findet bei der bezeichneten Stellung der Kurbel I
statt, wo nämlich dieselbe durch den Mittelpunkt des Kreises I, III geht. Es ist
hier tg ω = A₁͵₃/B₁͵₃ = (2 r ε n)/(rn) = 2 n oder tg ω = 2 sin 60; ω = 60°. Die Geschwindigkeit beträgt hier
(angegeben durch den Durchmesser des Kreises I, III)
Textabbildung Bd. 197, S. 108
ist also gleich der doppelten Kurbelgeschwindigkeit.
Die Minimal-Geschwindigkeit tritt bei der Stellung ω = 180° auf. Wir erhalten die Größe derselben leicht aus
der Gleichung des Kreises für V₃, indem wir ω = 180° setzen.
V₃ = – r ε m cos ω + r
ε n sin ω
mithin:
V = r ε
m = rε/2
Während also die Maximal-Geschwindigkeit gleich der doppelten
Kurbel-Geschwindigkeit ist, beträgt das Minimum derselben nur die Hälfte von
der der Kurbel. Wir erhalten also eine Geschwindigkeitsdifferenz gleich dem 1
1/2fachen der Kurbel-Geschwindigkeit.
Dieser Umstand spricht nun gerade nicht für die Downton-Pumpe. Denn während wir bei der 3 kurbeligen zusammengesetzten
einfach-wirkenden Pumpe die Geschwindigkeit derart constant fanden (Fig. 10), daß
man wohl bei einiger Schlauchlänge, wo die Elasticität desselben günstig mitzuwirken
im Stande ist, einen ziemlich gleichmäßigen Spritzenstrahl erhalten würde, dürfte
der einer Downton-Pumpe der betrachteten Art wohl
kaum zu gebrauchen seyn. Allerdings kann dieser Nachtheil wieder durch Anwendung
eines Windkessels gehoben werden, welcher doch wohl niemals bei denjenigen Pumpen
fehlt, welche zum Spritzen eingerichtet sind; und dann kommt die verhältnißmäßig
große Leistungsfähigkeit dieser Construction wieder zur Geltung.
Von diesen Gesichtspunkten aus erscheint die Downton-Pumpe immer da zweckmäßig, wo man auf einem kleinen Raum einen
kräftig wirkenden Apparat haben will. Und daraus erklärt sich die häufige Anwendung
dieser Construction bei größeren Schiffen. Es leiden jedoch viele dieser Pumpen an
einem Mangel, welcher freilich leicht genug zu beseitigen wäre. Da nämlich, wie
angedeutet, die Kolbenstangen der unteren Kolben die oberen treffen, also durch dieselben
hindurch gehen müssen, so liegt der Wunsch nahe, dieselben wegen der außerdem noch
anzubringenden Ventile so schwach wie irgend möglich zu halten.
Die Befestigung ist nun aber bei allen Pumpen, welche der Verfasser bisher zu sehen
Gelegenheit gehabt hat, excentrisch. Hieraus ergibt sich sofort bei einigermaßen
fester Verpackung der Kolben eine Neigung derselben zum Ecken, zum Herausgehen aus
der horizontalen Ebene. Da in Folge dieser Neigung eine größere Dimension (die
Diagonale) des Kolbens auftritt, so wird dadurch die Reibung noch vermehrt, das
Ecken abermals befördert, d.h. der Kolben setzt sich fest.
Wenn sich dieß auch schon durch möglichst loses Verpacken der Kolben vermeiden läßt,
für welches überhaupt, wie wir noch sehen werden, Vieles spricht, so ist doch eine
concentrische Fassung dieser Kolben sehr wünschenswerth.
Dieselbe ist nun durchaus nicht unmöglich, wie die Skizze Fig. 13 zeigt.
Es wird nur die Kolbenstange des unteren Kolbens massiv gemacht. Sie geht durch die
hohle Stange des mittleren und diese durch die abermals hohle Stange des oberen
hindurch, und trägt oben erst das nothwendige seitliche Befestigungsstück. Das durch
diese nicht zu umgehende excentrische Verbindung in der Stange auftretende
Biegungsmoment ist allerdings nicht gehoben, und es muß bei beiden Constructionen
die Stärke der Stange entsprechend gewählt werden. Aber die Neigung des Kolbens zum
Ecken ist umgangen, und außerdem ist die Anordnung der Ventile, deren Größe bei den
seitlichen Kolbenstangen recht bedenklich herabsinkt, einfacher und
zweckmäßiger.
Dichtungs-Vorrichtungen für die in einander gehenden Kolbenstangen sind wohl
bei diesen Pumpen nicht nothwendig. Es reicht, wenigstens bei geringen Druckhöhen,
aus, wenn die Stangen unten und oben so dicht anschließen, daß eine genügende
Führung stattfindet, ohne Reibung in größerem Maaße zu verursachen. Versieht man
außerdem die hohlen Kolbenstangen an ihren oberen Enden seitlich mit Löchern, so
wird, wenn einmal die Pumpe in Thätigkeit ist, Wasser hineinfließen und sich der
Nachtheil seiner Spielräume nur darauf beschränken, daß das Wasser dem Saugen und
Drücken entsprechend durch die schmale Spalte hin und her strömt. Der Verlust an
Arbeit ist bei obiger Annahme höchst gering und jedenfalls geringer als der durch
Reibung entstehende Arbeitsverlust bei Anwendung von Dichtungen. Ebenso verhält es
sich mit den Kolbenpackungen. Wenn diese auch wohl nicht gut bei langsam gehenden,
von Hand betriebenen Pumpen weggelassen werden können, so sollten sie doch aus
denselben Gründen möglichst leicht gehend gehalten werden.
Der einzige wichtigere Nachtheil dieses Principes liegt in dem schwereren Ansaugen
dieser so behandelten Pumpen, indem die Undichtheiten bei dem anfänglichen Aussaugen
der Luft allerdings schädlich wirken können. Aber auch dem ist leicht abgeholfen
durch das Angießen der Pumpe, für welches immer Einrichtungen vorhanden seyn
sollten. Die Arbeit welche nothwendig ist, um einen Eimer Wasser herbeizuholen und
hineinzugießen, ist jedenfalls abermals geringer, als der oft ungemein hohe
Arbeitsverlust durch übergroße Kolbenreibung. Ist alsdann das Bodenventil gut
construirt, so läuft bei dem Stillstand der Pumpe das Wasser auch nicht leicht ab,
und dieselbe wird immer leichter gebrauchsfähig seyn, als ein schwergehender
Apparat, der außerdem durch Verschleiß der Liderungen etc. noch vermeidbare Kosten
für Arbeitslohn und Material verursacht.
Diesem Princip folgend sind die Kolben der in der genannten Skizze angegebenen
Construction nur mit einer leicht anliegenden Leder-Manchette – eine
etwas ausgetriebene, durch ein umgezogenes Band befestigte Leder-Ringscheibe
– gedichtet. Die Ventile sind Gummiklappen, deren Anschlag durch
Klappenfänger regulirt wird. Die Welle wird durch Lager-Stopfbüchsen, welche
von oben her eingesetzt und durch Schrauben befestigt werden können, gehalten und
gedichtet. Der dieselbe enthaltende obere Raunt, eine cylindrische Erweiterung des
Pumpenstiefels, ist durch einen Deckel abgeschlossen, welcher mit einer
Verschraubung zum Angießen der Pumpe versehen ist. Die Ausgußöffnung befindet sich
in dem oberen Ende des Pumpenstiefels, und dient der ganze obere Raum des
Pumpenkörpers zugleich gewissermaßen als Windkessel.
Die hohlen Kolbenstangen enthalten oben Löcher zum Einlassen von Wasser behufs der
besseren Dichtung. Die Bewegung derselben geschieht durch Kurbelschleifen, welche in
dem oberen Aufsatz durch Schlitten geführt werden.
Bei der Construction dieser Pumpen hat man, wenn man dieselbe so gedrängt als möglich
ausführen will, besonders auf die Entfernung je zweier gegen einander arbeitenden
Theile von der Zapfenmitte zu achten. So muß z. B. die
Kolbenstangenlänge des unteren Kolbens um die Entfernung der Warzen plus der Kolbendicke plus
einem Spielraum von 1–2 Centimet. größer seyn, als die Kolbenstangenlänge des
mittleren Kolbens. Ebenso muß die Entfernung der Oberkante des zum mittleren Kolben
gehörenden Querstückes von der Zapfenmitte um die Warzenentfernung plus der Dicke des Querstückes plus einem Spielraum größer seyn, als die Entfernung der Oberkante des zum oberen
Kolben gehörenden Querstückes von seiner Zapfenmitte.
Die vorliegende Pumpe hat einen Wirksamen Hub von 62 Centimet. pro Umdrehung, während dieselben Kolben, jeder in einem eigenen Cylinder
laufend, zusammen einen wirksamen Hub von 42 Centimet. geben würden.
Andererseits beansprucht allerdings diese Pumpe eine Rohrlänge (mit Ansatz) von 120
Centimet., während dieselbe bei der dreifachen Pumpe zusammen nur circa 84 Centim. betragen würde, wohingegen diese wieder
zwei Ventile mehr erhalten müßte.
Es bleibt daher diese Anordnung mindestens stets da empfehlenswerth, wo ein
gedrungener kräftiger Apparat gewünscht wird.
Tafeln