| Titel: | Frictionsschrauben-Bewegungsmechanismus von J. Robertson in Glasgow. |
| Fundstelle: | Band 199, Jahrgang 1871, Nr. XXVII., S. 92 |
| Download: | XML |
XXVII.
Frictionsschrauben-Bewegungsmechanismus
von J. Robertson in
Glasgow.
Nach dem Engineer, October 1870, S.
261.
Mit Abbildungen auf Tab.
IV.
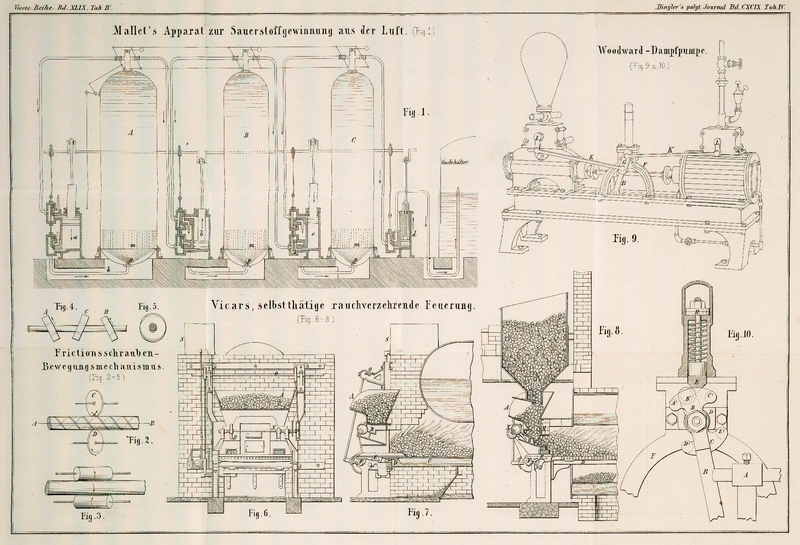
Robertson's
Frictionsschrauben-Bewegungsmechanismus.
Der Civilingenieur G. Lauder berichtete in der Versammlung
der British Association zu Liverpool über eine
Schraubenbewegung welche von J. Robertson vor einiger
Zeit erdacht worden ist, da dieselbe in gewissen Fällen eine zweckmäßig scheinende
Anwendung gestattet.
Ein Kreiscylinder, welcher sich um die Achse AB
frei verschieben und drehen läßt, ist mit einer doppelgängigen Schraubenspur
versehen, Figur
2. C und D sind
zwei unendliche dünne Scheiben, welche den Cylinder auf entgegengesetzten Seiten in
den Punkten M resp. D
berühren und deren Ebenen senkrecht zur Cylinderachse stehen. Bei der Drehung der
Scheiben um deren festgedachte Achsen werden jene der Schraubenspur folgen und der
Cylinder sowohl umgedreht als auch in der Längenrichtung verschoben, so daß jeder
Punkt seiner Oberfläche eine Schraubenlinie beschreibt. Der Cylinder wird demnach
durch die Reibung zwischen der Oberfläche desselben sowie der Scheiben C
und D ähnlich wie eine Schraubenspindel in einer festen
Mutter sich bewegen.
Drehen sich die Scheiben mit dem Umfang = u' nun n' mal um, so beschreiben die Berührungspunkte zwischen
Cylinder und Schieber eine Schraubenlinie von der Länge n' × u'. Die Anzahl der abgerollten
Schraubenumgänge gibt die der obigen Länge entsprechende Umdrehungszahl n für den Cylinder an.
Bezeichnet nun u den Cylinderumfang, α den Steigungswinkel der Schraubengänge, gleichzeitig den Winkel welchen die Achse des Cylinders
mit jenem der Scheiben einschließt, so besteht die leicht nachweisbare Relation
n'u' = nu/cos
α oder
die Tourenzahl des Cylinders: n =
n'u'/u cos α.
Die fortschreitende Bewegung des Cylinders s bei n Touren desselben ergibt sich eben so leicht:
s = nu tg
α
und wenn für nu der Werth
aus der ersten Gleichung substituirt wird, s = n'u'
sin α = Verschiebung des Cylinders.
Für die praktische Anwendung werden die Scheiben durch Rollen ersetzt, wie dieß auch
in Figur 3
angedeutet ist.
Diese Anordnung empfiehlt nun Robertson zum Geraderichten von
Wellen u. dgl. und um Stangen von beliebigem Querschnitt in dieser Art
gerade zu richten, ist neuerdings die Anordnung getroffen worden, daß – wie
in Figur 4 und
5 im
Grundritz und in der Seitenansicht – drei hohle Scheiben A, B und C geeignet gelagert
und bewegt werden und die beiden erstgenannten Scheiben die Stange an der einen
Seite, die dritte Scheibe aber an der entgegengesetzten Seite berühren.
Näheres über die Einrichtung dieser Vorrichtung ist aus unserer Quelle nicht zu
entnehmen.
Tafeln