| Titel: | Wasserstands-Anzeiger für mittlere Höhe; von F. H. Reitz, Civilingenieur in Hamburg. |
| Fundstelle: | Band 212, Jahrgang 1874, Nr. XXXI., S. 205 |
| Download: | XML |
XXXI.
Wasserstands-Anzeiger für mittlere Höhe;
von CF. H. Reitz, Civilingenieur in Hamburg.Aus dem officiellen Ausstellungsbericht über
„Geodätische Instrumente“ von Dr. W. Tinter, Professor an der k. k.
technischen Hochschule in Wien. Druck und Verlag der k. k. Hof- und
Staatsdruckerei, Wien 1874. Das soeben erschienene Heft (60) umfaßt:
Mathematische und allgemeine physikalische Instrumente; von Prof. Ferd. Lippich. – Astronomische und geodätische
Instrumente; von Prof. Dr. W. Tinter. (Mit 34 in den Text gedruckten Holzschnitten.) –
Magnetische und elektrische Apparate; von Prof. Dr.
A. v. Waltenhofen. – Uhren; von Fabrikant W.
Schönberger. (110 S. Preis 2 Gulden ö. W.)
Mit Abbildungen auf Tab.
IV.
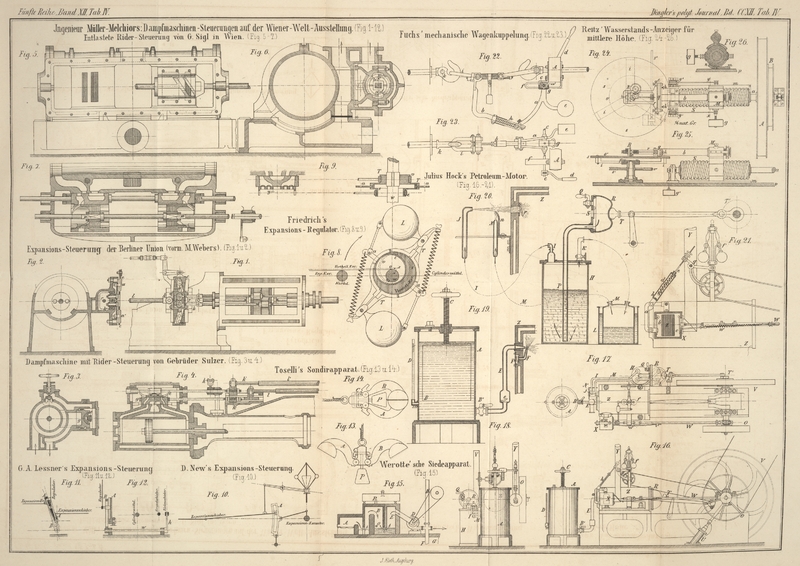
Reitz' Wasserstands-Anzeiger für mittlere Höhe.
Der von dem Hrn. Civilingenieur F. H. Reitz in Hamburg auf
Veranlassung des preußischen geodätischen Institutes der europäischen Gradmessung
construirte Wasserstands-Anzeiger soll dem schon lange gefühlten Bedürfnisse
abhelfen, die Höhe des Meeres, welche als Nullpunkt für andere Höhenangaben dient,
mit Sicherheit zu bestimmen.
In der Figur
24 ist der Grundriß, in Fig. 25 die Seitenansicht
und in Fig.
26 der Schnitt nach xy dieses von Reitz ersonnenen, von den Mechanikern Dennert und Pape in Altona
ausgeführten und in Wien 1873 ausgestellten Wasserstands-Anzeigers
dargestellt. Um die Scheibe A wickelt sich ein
Metalldraht, welcher mit einem Schwimmer in Verbindung steht, welcher in einem aus
Kupfer oder verzinktem Eisen hergestellten Schachte auf und nieder geht. Wenn der
Schwimmer sinkt, so dreht der Metalldraht die Scheibe A;
beim Steigen des Schwimmers wird A durch eine auf die
Scheibe B gewickelte Schnur, an welcher ein Gewicht
wirkt, in entgegengesetzter Richtung gedreht. Die Achse a der Scheiben A und B geht in die doppelgängige, äußerst sorgfältig gearbeitete Schraube S aus. Die Mutter für dieselbe ist in M; mit ihr ist durch den Stab b und das Querstück q der um die
Schraubenspitzen e drehbare Rahmen r in Verbindung, in welchem die Achse der Rolle R eingelagert ist. Letztere bewegt sich in radialer
Richtung auf der Glasscheibe s, welche durch ein Uhrwerk
in 24 Stunden eine volle Umdrehung macht. Es ist zu dem Ende mit der Büchse, mit
welcher die Scheibe s auf einem verticalen Zapfen ruht,
eine am Umfange mit Schraubengewinden versehene Scheibe s' in Verbindung, in welche Gewinde die Schraube s'' eingreift, welche eben durch das Uhrwerk gedreht wird. Die Metallfeder
f kann mittels Schrauben so gespannt werden, daß
sich die Büchse mit s um den Verticalzapfen leicht aber
doch sicher dreht. Die Führung der Schraubenmutter wird durch den Ansatz n (Fig. 26), welcher sich durch das
entgegenwirkende Gewicht g an die mit einer scharfen,
parallel zur Achse von S gestellten Kante versehene
Metallplatte m lehnt, bewerkstelliget.
Zur Aufhebung des todten Ganges dienen die Gegengewichte g'.
Nach einer Mittheilung von Reitz in der
„Allgem. deutschen polytechn. Ztg.“ 1874, S. 193
wird der jetzt für das geodätische Institut auszuführende Apparat statt mit
Schraube mit Trieb und Zahnstange eingerichtet. Außerdem wird zur Controlle eine zweite
Rolle auf der Glasscheibe gleiten und den mittleren Wasserstand angeben.
Zugleich ist der für das Institut bestimmte Apparat mit einem die ganze
Fluthcurve zeichnenden Diamantstift und Cylinder versehen, wodurch eine
allen wissenschaftlichen und praktischen Zwecken entsprechende Combination
dargeboten wird. Die Red.
Theorie des Apparates. Bei irgend einem Wasserstande,
etwa bei Null des Pegels, stehe die Rolle R in der Mitte
o der Scheibe s; beim
Steigen des Wassers rückt die Rolle von o nach links
gegen o'. Würde sich die Scheibe A einmal umdrehen, so hat sich auch der Wasserstand um die Größe des
Umfanges U der Scheibe A
geändert. Wäre etwa für die Aenderung H im Wasserstande
die Verschiebung der Rolle o o
' und ist g die Höhe
eines Schraubenganges, so ist
oo' = H
g/U und umgekehrt
H = oo'
U/g . . . . . . . . 1.
Man erhält demnach die Wasserstands-Höhe H, wenn
man den Abstand der Rolle vom Mittelpunkte der Scheibe mit dem, einem bestimmten
Instrumente zukommenden, constanten Coefficienten U/g multiplicirt.
Um zu erfahren, um wie viel sich der Auflagepunkt der Rolle R auf der Scheibe s durch die vereinte Wirkung
der wechselnden Wasserstände und der Drehung der Scheibe s radial weiter bewegt, bedenke man Folgendes:
Ist u der Umfang der Rolle R,
ferner die am Zählrädchen und an der getheilten Trommel abgelesene Umdrehungszahl
z, so ist der Weg σ eines Punktes des Umfanges von R.
σ = u . z . . . . .
2.
In einer unendlich kurzen Zeit dreht sich die Scheibe durch das Uhrwerk um dφ, die hiermit verknüpfte Drehung der Rolle R sei dσ so ist, wenn
d den Abstand der Rolle vom Mittelpunkte der Scheibe
zur selben Zeit bedeutet,
dσ = d . dφ
Durch Integration erhält man:
σ = ∫d .
dφ . . . . . 3.
das ist, den Weg σ, um
welchen sich ein Punkt des Umfanges von R in einer Zeit,
welcher der Drehungswinkel φ entspricht, weiter
bewegt hat.
Die Verbindung der Gleichung 2 mit 3 gibt:
u . z = ∫d . dφ . . . . . 4
Der Ausdruck ∫d . dφ stellt aber den Inhalt
einer Fläche dar, welche sich ergibt, wenn man die Abstände d der Rolle von Mittelpunkte der Scheibe als Ordinaten und die zugehörigen
Zeitbögen für den Halbmesser = 1 als Abcissen betrachtet.
Will man aus dieser Fläche den mittleren Werth von d =
m finden, so braucht man nur durch die bezügliche
Abscissenlänge, hier φ zu dividiren; es ist
m = (∫d .
dφ)/φ = (u
. z)/φ . . . . . 5
Hat man aber m, den mittleren Abstand der Rolle vom
Mittel-Punkte der Scheibe für einen gewissen Zeitabschnitt, so findet man
nach Gleichung 1 hieraus den mittleren Wasserstand; es ist H = m . U/g oder mit Rücksicht auf 5
H = U/g . (u . z)/φ . . . . . I
Für ein vorliegendes Instrument ist U/g eine constante Größe; sei C = (U/g) u, so wird nach I
H = C/φ . z . . . . II.
Man wird sich eine Tabelle rechnen, welche mit dem Argumente φ den Werth C/φ gibt.
Es läßt sich auch die Anordnung so treffen, daß C/φ für eine Stunde oder für eine Minute eine runde
Zahl, etwa 100 oder 10 werde.
Eigenschaften des Apparates.
1. Die Achse der Rolle R muß parallel zur Scheibe s sein.
2. Die Kante der Metallplatte m muß parallel zur Achse
der Schraube S sein. Diese beiden Eigenschaften werden
vom Mechaniker so genau als möglich herzustellen getrachtet und sind für den
Beobachter keine Correctionsvorrichtungen vorhanden.
3. Die Achse der Rolle R muß mit der Richtung der
radialen Bewegung derselben, also mit der Achse der Schraube S parallel sein. Mit Hilfe der Schräubchen h
kann ein etwaiger Fehler hierin verbessert werden. (Es darf sich nämlich keine
Drehung der Rolle R ergeben, wenn bei ruhiger Lage der
Scheibe s die Scheibe A
gedreht wird.)
4. Muß der Berührungspunkt der Rolle bei seiner Bewegung durch den
Drehungsmittelpunkt der Scheibe s gehen. Mittels der
Schrauben e (Figur 24) kann ein
etwaiger Fehler berichtigt werden. (Ein vom Mechaniker beigegebenes Maß, welches die
Entfernung von dem Ende eines der drei Arme i von einem
bestimmten Punkt des Rahmens r angibt, dient zur Prüfung
dieser Eigenschaft.)
Bestimmung der ConstantenC. Man stellt die Scheibe A
so, daß diese Stellung einem bestimmten Wasserstande H
entspricht, und läßt dann die Scheibe s eine größere
Anzahl von Umdrehungen machen; aus Gleichung H folgt
dann, da H, φ und z
bekannt ist:
C = (H . φ)/z . . . . .
III.
Tafeln