| Titel: | Fortschritte in der Uhrmacherkunst; von F. Frese, Assistent für das Maschinenfach am k. Polytechnicum zu Hannover. |
| Autor: | F. Frese |
| Fundstelle: | Band 214, Jahrgang 1874, Nr. XLII., S. 177 |
| Download: | XML |
XLII.
Fortschritte in der Uhrmacherkunst; von F. Frese, Assistent für das
Maschinenfach am k. Polytechnicum zu Hannover.
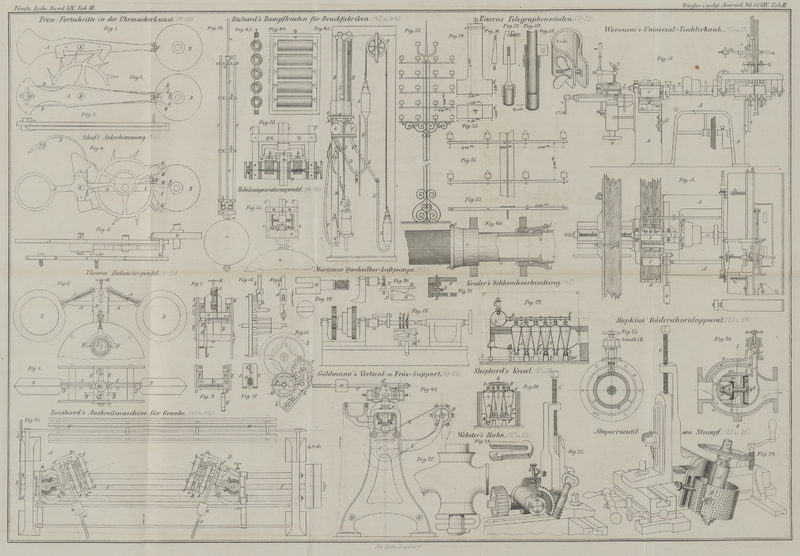
Mit Holzschnitten und Abbildungen auf Tab. III.
Frese, über Fortschritte in der Uhrmacherkunst.
1. Verbesserte Ankerhemmung von W. G.
Schoof. (Figur 1 bis 5.)
Obgleich England sich in der Herstellung guter Uhren jeder
Art auszeichnet, so kann es doch in Bezug auf Billigkeit der Production einen
Vergleich mit anderen Ländern (Frankreich, Schweiz, Amerika) nicht aushalten. Hier
ist also noch ein vielversprechendes Feld für Erfinder, und bei den Verbesserungen
der Ankerhemmung, welche Schoof (Engineering, September 1874 S. 254) sich kürzlich hat patentiren lassen,
ist in der That – außer auf Sicherung eines exacten Ganges der Uhr –
auf Einfachheit, also auf Billigkeit der Herstellung das Hauptaugenmerk gerichtet
worden.
Schoof's Verbesserungen bestehen zunächst in
Vereinfachung derjenigen Theile der Hemmung, durch welche das Zusammenwirken
zwischen Unruh und Ankerhebel erreicht wird, und dann in Construction zweier
Sicherungen, welche alle durch äußere Erschütterungen hervorgerufenen Störungen in
der Wirkungsweise der Unruh unschädlich machen sollen. Außerdem weicht der
Patentinhaber noch in einigen Constructionen von den gewöhnlichen ab; er setzt
nämlich das Steigrad zwischen Anker und Unruh, wendet statt des sonst gebräuchlichen
15zähnigen Steigrades, bei welchem der Anker auf eine Bogenlänge von 2 1/2 Zähnen
wirkt, ein solches an mit 10 Zähnen, wobei der Anker den Raum zwischen 1 1/2 Zähnen
beherrscht, und macht die Steigradzähne von Gold, um Oel an den Ankerpaletten
entbehren zu können. Der Nutzen dieser Einrichtungen ist jedoch noch fraglich.
Figur 1 zeigt
Schoof's Ankerhemmung in ihrer einfachen Form. An der
auf der Achse der Unruh befindlichen Scheibe B (dem
sogenannten Plateau) ist ein kleiner sichelförmiger Ausschnitt, in welchem der Stift F befestigt ist. Dieser faßt zwischen die beiden Stifte
C, C des Ankerhebels und hat so dieselben Functionen
zu erfüllen, wie bei gewöhnlichen Hemmungen die sogen. Ellipse, welche sich zwischen
den Gabeln des Hebels bewegt. Diese Einrichtung zeichnet sich durch ihre Einfachheit
aus; sie soll übrigens auch einen sehr sicheren Gang zur Folge haben und die
schädlichen Wirkungen von äußeren Erschütterungen auf das Spiel der Unruh
abschwächen. Ob sie diese Vortheile in dem Maße besitzt, wie angegeben wird, muß
erst durch die Erfahrung festgestellt werden; jedenfalls bietet sie den Vorzug, daß
man bei ihr sehr leicht Sicherheitsmechanismen anbringen kann. Die Figuren 2 und 3, 4 und 5 zeigen zwei
derartige Mechanismen, welche Schoof bei seiner Hemmung
anwendet.
Die Sicherung Fig.
2 und 3 ist fest mit dem Ankerhebel verbunden; sie soll vorzugsweise für
feinere Uhren und für Chronometer angewendet werden. Hier müssen, ähnlich wie bei
gewöhnlichen Ankeruhren, feste Anschlagstifte bezw. Messer angebracht werden, um zu
große Ausschläge des Ankerhebels zu verhindern. Die Einrichtung der Sicherung ist
folgende. An dem Schwänze des Ankerhebels A ist bei h eine Feder D befestigt,
welche an beiden Seiten rechtwinkelig umgebogen ist und mit ihren beiden Enden d, d zwischen die Gabeln H,
H des Ankerhebels greift. Diese Gabeln haben den alleinigen Zweck, die
beiden Federenden festzuhalten, und müssen letztere, damit dieses geschehen kann, um
die Stärke des Ankerhebels breiter sein als die Feder selbst. In dem Plateau B ist ein Stein E
eingelassen, welcher mit den beiden Hörnern Hd in
Wechselwirkung tritt. Während des normalen Ganges der Uhr bewegt sich der Stift E innerhalb der beiden Hörner Hd,
Hd. Sobald aber die Unruh in Folge einer Erschütterung eine sehr heftige
Schwingung macht, wird der Stein E nach Zurücklegung
eines vollen Umschwunges gegen die äußere Kante von d
schlagen, dann aber wegen der Elasticität der Feder diese soweit durchdrücken, daß
er vorbeipassiren kann, und so wieder in das Innere der Gabeln gelangen. Bei der
rückgängigen Drehung, welche dann die Unruh machen muß, um ihren normalen
Bewegungszustand wieder zu erlangen, wird der Ankerhebel mitgenommen, der Stein E drückt das andere Ende der Feder durch, gelangt in das
Innere, und der normale Gang ist wieder hergestellt. Durch diese Einrichtung wird
einmal der heftige Stoß des Steines gegen die äußere Kante der Gabel selbst
geschwächt (wegen der Elasticität der Feder) und dann die durch die Erschütterung
hervorgebrachte heftigere Schwingung der Unruh, welche bei gewöhnlichen Uhren einen
rascheren. Gang zur Folge hat, bis auf das normale Maß reducirt.
Eine zweite Sicherung, welche bei Uhren der gewöhnlichen Art angebracht werden kann,
ist in Fig. 4
und 5
dargestellt. Hier ist ein besonderer Hebel L, drehbar um
den Punkt O (Fig. 5) eingeschaltet, der
jedoch durch eine Feder D, wirkend auf den kürzeren, an
seiner Endfläche verbreiterten Hebelarm von L, in seiner
normalen Lage erhalten wird. Der Ankerhebel ist auch hier mit zwei Gabeln versehen,
welche wie bei gewöhnlichen Uhren mit dem Steine E am
Plateau in Wechselwirkung treten. Bei normalem Gange versehen die beiden am Hebel
L befestigten Stifte G,
G die Functionen der unbeweglichen Anschlagstifte oder Messer anderer
Uhren, indem sie zu große Ausschläge des Ankerhebels verhindern. Wenn jedoch starke
Erschütterungen die Unruh derartig afficiren, daß sie einen vollen Umschwung macht,
so schlägt der Stein E gegen die äußere Kante der Gabel;
diese wird gegen einen der beiden Stifte G gedrückt und
wegen der Elasticität der Feder D soweit fortgerückt,
daß der Stein passiren und in das Gabelinnere treten kann. Er nimmt dann bei dem
Rückschwung der Unruh zunächst den Ankerhebel wieder mit, schlägt nach beinahe
beendigtem Schwung gegen die andere äußere Kante des Ankerhebels, drückt diesen
soweit durch, bis er vorbei kann, und der normale Zustand ist wieder hergestellt.
Diese Sicherung erfüllt also denselben Zweck, wie die erste, sie hat jedoch vor ihr
den Vorzug, daß sie vollständig frei vom Ankerhebel ist und diesen daher nicht mit
belastet wie jene.
Beide Arten der Sicherung scheinen praktisch und gut zu sein; – verhindern sie
doch einmal alle Unregelmäßigkeiten des Ganges in Folge von Erschütterungen und
machen außerdem das bei gewöhnlichen Uhren so häufig vorkommende Abspringen des
Steines, oder Durchbiegen bezieh. Brechen der Unruhachse fast unmöglich. In der That
haben auch Versuche, die an verschiedenen Uhren, welche mit diesen Mechanismen
versehen waren, angestellt wurden, die günstigsten Resultate ergeben, da es sehr
schwer, ja fast nicht möglich war, durch irgend welche äußere Erschütterungen diese
Uhren in ihrem Gange zu stören.
2. Uhren von Y. M. Thomas. (Figur 6 bis
13.)
Zur Regulirung von Pendeluhren kann man bekanntlich verschiedene Pendel verwenden. Am
geeignetsten und deshalb bei weitem am gebräuchlichsten ist das Kreispendel; weniger
oft werden Centrifugal- oder Balancierpendel angewendet – und eine
ganz untergeordnete und für Uhrwerke zur Zeitbestimmung gar keine Bedeutung hat das
Torsionspendel. Es läßt sich jedoch nicht verkennen, daß auch letztere beiden
(Centrifugal- und Balancierpendel) ihre Vorzüge haben, und hat sich Y. M. Thomas (Boulevard
Ménilmontant 99 in Paris) – nach Berichten des Bulletin de la Société d'Encouragement;
September 1874 S. 433 u.s.f. – zur Aufgabe gestellt, diese zu vervollkommnen,
indem er theils gewisse Vorzüge des Kreispendels auf sie überträgt, theils ihre
speciellen Eigenthümlichkeiten in geschickter Weise auszunützen sucht.
Die wesentlichsten Verbesserungen beziehen sich auf das Balancierpendel. Bekanntlich
steht die Länge eines Kreispendels in directem Verhältniß zu dem Quadrat der
Schwingungsdauer; will man diese verdoppeln, so müßte man die Pendellänge
vervierfachen. Anders ist es dagegen bei dem Balancierpendel. Hier ist die
Schwingungsdauer dieselbe wie beim Spiel eines gleichbelasteten Waagebalkens; sie
hängt ab von zwei Factoren: der Länge der Hebelarme und der verticalen Entfernung
des Aufhängepunktes vom Schwerpunkte der schwingenden Massen. Hat man über die Länge
der Pendelarme verfügt, so kann man durch Wahl des Aufhängepunktes noch immer die
Schwingungsdauer beliebig bestimmen, und würde man diese deshalb, falls es
wünschenswerth erscheinen sollte, im Vergleich zum Kreispendel nach Willkür
vergrößern können. Wesentlicher als dies ist jedoch der damit zusammenhängende
Vortheil, daß das Balancierpendel, richtig aufgehängt, eine bedeutend geringere
Bewegungskraft zur Aufrechterhaltung seiner Functionen absorbirt als das
Kreispendel. Diesen Umstand benützt Thomas, um bei
verhältnißmäßig geringer Triebkraft einen sehr langen Gang der Uhr zu erzielen. Er
glaubt, es so weit treiben zu können, daß seine Balancierpendeluhr innerhalb eines
Zeitraumes von 5 Jahren nicht aufgezogen zu werden braucht. Außerdem ist die
Compensation eine verhältnißmäßig einfache, bei der die Anwendung verschiedener Metalle vollständig vermieden wird. Der
ganze Kunstgriff besteht hierbei in der richtigen Wahl des Winkels, welchen die
Pendelstangen mit der Horizontalen bilden. Wenn nämlich durch die metallische
Ausdehnung der Pendelstangen die Linsen sich mehr von einander entfernen und dadurch
eine Verlängerung der Schwingungsdauer hervorbringen, so müssen sie wegen des
Winkels, welchen die Pendelstangen mit der Horizontalen bilden, sich gleichzeitig
etwas senken, was eine raschere Bewegung zur Folge hat. Der betreffende Winkel ist
demnach so zu bestimmen, daß die Verzögerung des Ganges, hervorgerufen durch die
größere Entfernung der Linsen von einander, und die Beschleunigung, bewirkt durch
das gleichzeitige Senken derselben, sich gerade aufheben. Ob eine absolut genaue Compensation auf solche Weise zu
erreichen, ist wohl fraglichUm zu untersuchen, wie sich die Linsenschwerpunkte in Folge von
Temperaturveränderungen verschieben müssen, damit eine vollständige
Compensation stattfinde, ist das Pendel in nebenstehender Figur in
einfachen Linien dargestellt. O bezeichnet den
Aufhängepunkt des ganzen Systems; S₁ sei
der Schwerpunkt der Linsen, S₂ der
Schwerpunkt des Dreieckkörpers abc mit Einschluß
aller an der Schwingung theilnehmenden Körper außer den Linsen, endlich S den Schwerpunkt des ganzen Systems. Werden nun
folgende Bezeichnungen eingeführt:Textabbildung Bd. 214, S. 180T = Trägheitsmoment sämmtlicher an der
Schwingung theilnehmenden Körper in Bezug auf die durch 0 gehende
horizontale Drehachse;TL = Trägheitsmoment einer Linse in
Bezug auf die durch ihren Mittelpunkt (A bezieh.
B) gehende horizontale Drehachse;TΔ = Trägheitsmoment des
Dreieckkörpers abc mit Einschluß aller übrigen
schwingenden Theile außer den Linsen in Bezug auf die durch den gemeinsamen
Schwerpunkt S₂ gehende horizontale
Drehachse;M = 2m + m₁ = Masse des ganzen schwingenden
Systems;2m = Masse der beiden Linsen;m₁ = Masse der übrigen schwingenden
Körper;so ergibt sich die Entfernung l des Schwingungspunktes des ganzen Systems vom Aufhängepunkt
aus:1) l = T/Mϱ
Weil aber:T = 2(T
L + mr²) + TΔ + m₁r₁²und Mϱ = 2m r sin
α + m₁r₁ ist, so folgt:Textabbildung Bd. 214, S. 180Wird nun r₁ als constant angenommen und
deshalb abkürzungsweise2T
L + TΔ + m₁r₁² = C (constant)und m₁r₁ = C₁ (constant)gesetzt, so ist:Textabbildung Bd. 214, S. 180Die Schwingsdauer des Pendels ist demnach:Textabbildung Bd. 214, S. 180Diese Größe muß bei richtiger Compensation stets constant sein, woraus die
BedingungTextabbildung Bd. 214, S. 180folgt oder, wenn C/2m = e, C₁/2m = c₁, K/2m = k gesetzt wird:Textabbildung Bd. 214, S. 180und wenn abkürzungsweise c₁k – c = k₁
gesetzt wird:5) r² = r sin
α . k + k₁.Textabbildung Bd. 214, S. 182Aus dieser Gleichung ist das Gesetz zu erkennen, nach welchem bei
Veränderung von r (in Folge von
Temperaturveränderungen) α sich
ändern muß, damit die Schwingungsdauer stets dieselbe bleibt; mit
anderen Worten: r² = r sin α . k + k₁ ist die Gleichung
derjenigen Linie, bezogen auf den Punkt O
als Anfangspunkt eines polaren Coordinatensystems, in welcher die
Linsenschwerpunkte sich bewegen müssen, wenn eine richtige Compensation
stattfinden soll.Um über die Eigenschaften der betreffenden Linie näheren Aufschluß zu
erhalten, werde das polare Coordinatensystem mit einem orthogonalen
vertauscht, dessen Anfangspunkt ebenfalls O
sei.Es ist dann:r² = x² + y²r sin α = y
und daher die Gleichung der Curve, bezogen auf dieses
neue System:6) x² + y² = ky + k₁welches die Gleichung eines Kreises symmetrisch zur
Y-Achse ist. Um die
Mittelpunktsgleichung des Kreises zu finden, ist eine zweite
Coordinatentransformation vorzunehmen, bei der jedoch die Y-Achse dieselbe bleibt, da der Kreis in
Bezug auf sie symmetrisch verläuft. Der Coordinatenanfang werde um β auf der Y-Achse verschoben; dann ist, wenn der Symmetrie halber auch
den x-Werthen Indices hinzugefügt werden,
die Gleichung des Kreises, bezogen auf das System X₁Y₁:7) x₁² + y₁² + 2y₁β + β² – ky₁
– kβ – k₁ = 0.Da der neue Coordinatenanfang im Kreismittelpunkte liegen soll, so bestimmt
sich β aus:2β – k = 0β = k/2.Die Kreisgleichung nimmt demnach schließlich die Form an:x₁² + y₁² + β²
– kβ – k₁ = 08) x₁² + y₁² = k²/4 + k₁aus welcher hervorgeht, daß, wenn eine wirkliche
Compensation erfolgen soll, die Linsenschwerpunkte sich unter dem Einflusse
von Temperaturveränderungen in einem Kreise bewegen müssen, dessen
Mittelpunkt um β = k/2 unter dem Aufhängepunkte liegt, und dessen Radius R = √(k²/4 + k₁,) wobei jedoch
vorausgesetzt ist, daß die Entfernung des Schwerpunktes S₂ der schwingenden Massen mit Ausnahme
der Linsen vom Aushängepunkte bei allen Temperatureinflüssen sich nicht
ändert.Würden die Längenveränderungen der Pendelstangen in Folge von
Temperatureinflüssen allein die Lage der Linsen bestimmen, so würden diese
sich in den Richtungslinien der Stangen verschieben, und müßten diese
Richtungslinien deshalb so bestimmt werden, daß sie Tangenten an dem Kreise
obiger Gleichung wären – in den Punkten, in welchen die
Linsenschwerpunkte bei mittlerer Temperatur sich befinden. Nun wird aber
auch die Formänderung des Dreieckstückes abc von
Einfluß sein auf die Lage der Linsenschwerpunkte, und sind deshalb die
Richtungslinien der Pendelstangen so zu wählen, daß die resultirende
Bewegung der Linsenschwerpunkte in Folge der Längenveränderung der
Pendelstangen und der Formveränderung des Dreieckstückes abc möglichst genau mit der bewußten Kreislinie
zusammenfällt.; jedoch versichert Thomas, daß er dem Gange mehrerer seiner
Uhren mit großer Aufmerksamkeit gefolgt sei und daß sich nicht die mindeste
Differenz mit Kreispendeluhren herausgestellt habe.
In den Figuren
6 bis 10 ist Thomas' neues Balancierpendel
dargestellt. A ist der Balancier; B, B sind die beiden Linsen, deren Gewicht natürlich vollständig gleich sein muß. Die
Befestigung derselben an dem Balancier A geschieht durch
die Arme C, C und die vier Zapfen D, welche sämmtlich fest mit dem Balancier verbunden sind. Die Stangen C, C sind in den oberen Zapfen D fest verschraubt, während sie durch die unteren frei hindurchgehen. In
dem Gehäuse E findet die Aufhängung des Pendels statt.
Zwei an den Seitenwänden von E befestigte Zapfen tragen
die feinen Metallfedern F, F, welche unten durch eine
Traverse G verbunden sind. Diese hat in der Mitte zwei
Nuthen, in welche der Balancier eingelassen wird. Der mit dem Hemmungsrade I in Eingriff kommende Anker H ist durch den rechtwinkelig umgebogenen Arm H₁ an der Traverse befestigt. Die Zähne des Hemmungsrades sind
ebenfalls von abweichender Construction und so geformt, daß die Ankerpaletten sie
nur während des Zeitpunktes der Ruhe berühren. Die Platte J, welche mit einem langen verticalen Einschnitt versehen ist, dient
ferner dazu, das Pendelgehäuse an dem Uhrgehäuse in der richtigen Lage
festzuschrauben. Schließlich ist der Balancier A noch
mit einer Stellschraube K versehen, welche auf die
Traverse G drückt und zur Erreichung des wichtigen
Zweckes dient, den Balancier mit Pendelstangen und Linsen in verticaler Richtung zu
verstellen und so den Abstand zwischen Aufhängepunkt und Schwingungspunkt –
also die Schwingungsdauer zu reguliren.
Außer diesen Neuerungen finden wir bei den Thomas'schen
Uhren noch besondere Mechanismen angewendet, einmal um die Wochentage anzuzeigen und
dann um die Zahl der seit dem letzten Aufziehen verflossenen Tage in fortlaufender
Reihenfolge anzugeben, welches letztere bei diesen langgehenden Uhren wohl nicht
überflüssig sein dürfte. Der Wochentagezeiger macht in einer Woche oder in 14 Tagen
eine Umdrehung, während die Umdrehungszeit des zweiten Zeigers je nach dem Gange der
Uhr ein, auch mehrere Jahre beträgt.
Einen Mechanismus zur Bewegung des Tagezeigers zeigt Fig. 11. Die mit dem
Uhrgehäuse verbundene Platte L trägt im Verein mit der
Brücke O zwei Zahnräder N
und M, welche mit einander im Eingriff stehen. An der
Achse von M ist der Tagezeiger P befestigt. Die Feder Q drückt mit ihrem
oberen Ende gegen einen Zahn des Rades N – und
zwar um zu verhindern, daß dieses Rad zur Zeit eine größere Drehung als um einen
Zahn macht. An ihrem unteren Ende ist die Feder mittels einer Druckschraube an der
Platte L befestigt; das Schraubenloch ist länglich, um
die Lage der Feder bequem justiren zu können, ehe sie dauernd befestigt wird. Die
Bewegung der Räder M und N
wird durch das Stundenrad R hervorgebracht; an einem Arm
desselben befindet sich
nämlich ein kleiner Stift S, welcher, sobald er in
Berührung mit dem Rad N kommt, diesem eine Drehung um
einen Zahn mittheilt. Dadurch wird auch das Rad M um
einen Zahn gedreht; hat dieses nun, wie in unserer Abbildung, 28 Zähne, so wird, da
das Stundenrad in 12 Stunden eine Drehung macht, alle 24 Stunden das Rad M um 2 Zähne sich fortbewegen und daher in 14 Tagen
seine Drehung beendigt haben. Soll die Umdrehungszeit auf 8 Tage reducirt werden, so
kann man entweder ein 14zähniges Rad statt des 28zähnigen anwenden, oder aber das
Stundenrad mit 2 diametral gegenüberstehenden Stiften S
versehen, so daß das Rad M alle 6 Stunden um einen Zahn
fortrückt.
Thomas stellt auch Balancierpendeluhren her, bei denen
das Zifferblatt den 24 Tagesstunden entsprechend getheilt ist, so daß 12 Ziffern die
Tageszeit, die anderen 12 die Nachtzeit angeben. Der Stundenzeiger macht dieser
Theilung gemäß in 24 Stunden eine Umdrehung, während der Minutenzeiger in 2 Stunden
sich einmal dreht. Bei diesen Uhren verwendet Thomas
beispielsweise eine Spiralfeder, welche sonst für 8tägige Uhr gebräuchlich, hier
aber im Stande ist, den Gang der Uhr 400 Tage lang zu unterhalten.
Der Wochentagezeiger wird hier in etwas anderer Weise als oben bewegt, um eine
concentrische Bewegung mit den Hauptzeigern zu erreichen. Derselbe ist an der Hülse
eines 14zähnigen Rades befestigt, das lose auf der Achse des Stundenrades sitzt,
jedoch durch eine gegen einen seiner Zähne drückende Feder in unveränderter Lage
erhalten wird, so lange bis eine zweite Feder – an dem Stundenrad befestigt
und mit diesem sich drehend – gegen einen kleinen am Uhrgehäuse angebrachten
Daumen gepreßt und dadurch durchgebogen wird, in Folge dessen zwischen zwei Zähne
des oben erwähnten 14zähnigen Rades greift und dieses um einen Zahn fortschiebt.
Die Bewegung des die Tage seit dem letzten Aufziehen in fortlaufender Reihenfolge
angebenden Zeigers geschieht direct durch Zahnradübersetzung vom Zahnkranz des
Federhauses aus.
Schließlich ist noch die Verbesserung zu erwähnen, welche Thomas bei der Centrifugalpendeluhr angebracht hat. Es ist Regel in der
Uhrmacherkunst, daß – um bei einem Pendel die größte Regelmäßigkeit in der
Bewegung zu erzielen, deren es überhaupt fähig ist – man es einen möglichst
großen Theil seiner Schwingung vollständig unabhängig von der Bewegungskraft machen
lassen muß; mit anderen Worten, je kürzer die Zeit ist, während der bei einer
Schwingung die Bewegungskraft auf das Pendel einwirkt, um so größer ist die
Gleichförmigkeit seiner Bewegung. Bei den bisher gebräuchlichen Pendeluhren war nun das
Pendel dem beständigen Einflusse der bewegenden Kraft
unterworfen, und wurden so alle Unregelmäßigkeiten desselben auf das Pendel mit
übertragen. Dieses hat Thomas dadurch beseitigt, daß er
auch hier eine Hemmung einschaltet, welche das Pendel während einer gewissen Zeit
seiner Schwingung unabhängig von der Bewegungskraft macht. Dieselbe ist in Fig. 12 und
13
dargestellt. Das Steigrad a greift mit seinen Stiften
abwechselnd in die diametral gegenüberstehenden Einschnitte e, e der auf der Pendelachse b befestigten
Hülse d, und ist also nur während dieses Eingriffes eine
Einwirkung der Kraft auf das Pendel vorhanden. Diese Hemmung erfüllt gleichzeitig
einen zweiten nicht minder wichtigen Zweck – den nämlich, die Minuten in
Secunden zu theilen, und so die Anbringung eines Secundenzeigers an Uhrwerken,
welche am wenigsten hierzu geeignet schienen, zu erleichtern.
3. Hebelcompensationspendel. (Fig. 14 bis
16.)
Schließlich dürfte hier der geeignete Ort sein, noch einige Worte über ein
Compensationspendel zu sagen, welches allerdings nicht neu, aber doch noch äußerst
wenig bekannt ist und wohl in weiteren Kreisen Interesse erregen dürfte. Dasselbe
ist in seiner ursprünglichen Gestalt in Fig. 14 bis 16
dargestellt.
Wie man leicht erkennt, wird die Compensation hier durch die ungleiche Ausdehnung
verschiedener Metalle bei gleichen Temperaturveränderungen und durch Hebelwerke
bewirkt. Die Pendelstange a ist bei b mit der Stange c fest
vereinigt. Diese trägt bei d ein Querstück e, welches mit den Stangen f,
f und dem unteren Querstück g einen festen
Rahmen bildet, der durch die Bügel h versteift wird. Die
Mittelstange c, welche frei durch die Bügel h hindurchgeht, ist von einem Metalle, dessen Ausdehnung
bezieh. Zusammenziehung durch Temperaturveränderungen bedeutender ist als jene der
Stangen f, f unter gleichen Umständen. Die Stange c ist unten mit zwei verstellbaren Schraubenmuttern i, i (Fig. 15) versehen, welche
auf die äußeren Arme α der Hebel k, k einwirken. Die inneren Arme β dieser Hebel greifen unter das Plättchen l, und tragen so die an der frei im Querstück g spielenden Stange m aufgehängte Linse n. Bei erhöhter Temperatur wird sich nun die
Mittelstange stärker ausdehnen als die Seitenstangen; in Folge dessen werden die
Schraubenmuttern i, i die Hebelarme α nach unten drücken und so ein Erheben der
Hebelarme β und damit der Linse um das Maß der
Senkung bewirken. Umgekehrt wird sich bei eintretender Kälte die Stange C um mehr als die übrigen Stangen zusammenziehen, die Arme α gehen folglich aufwärts und die Linse senkt
sich um so viel, daß die normale Länge wieder hergestellt wird.
Nimmt man an, daß sich in Folge erhöhter Temperatur die Pendellänge L (Entfernung des Aufhängepunktes vom Schwingungspunkte)
um λ + λ₁ vergrößere – wobei λ die Verlängerung vom Aufhängepunkte bis zum Querstück g und λ₁ die
Verlängerung der Stange m bezeichnet – so muß
diese ganze Verlängerung λ + λ₁ durch die gleichzeitige Ausdehnung der
Stange c (von d an
gerechnet), welche λ₂ betragen möge,
compensirt werden. Die Mehrsenkung der Schraubenmuttern i,
i im Vergleich zum Querstück g, an welchem die
Hebel ihren Drehpunkt haben, beträgt λ₂
– λ, und ergibt sich daher zur Berechnung
der Hebellängen die Proportion:
(λ₂ – λ) : (λ + λ₁) = α
: β
Gegenüber dem Quecksilbercompensationspendel hat dieses mit dem Jürgensen'schen Rostpendel u.a. jedenfalls den Vortheil größerer
Genauigkeit gemein, da bei jenem die Höhentemperaturunterschiede eines Zimmers stets
die Richtigkeit der Compensation beeinträchtigen werden; außerdem wird es leicht
durch Verstellen der Schraubenmuttern i, i justirt
werden können. Doch ist das Pendel noch Verbesserungen fähig, die sich vorzüglich
darauf werden erstrecken müssen, eine ungleichmäßige Veränderung der Hebelarme α durch ungleiches Bewegen der Schraubenmuttern
unmöglich zu machen. Zu diesem Zwecke würde man vielleicht, wie in Fig. 16 angedeutet ist,
eine etwas veränderte Anordnung des Hebelmechanismus mit Hilfe einer rechts-
und linksgängigen Schraube, deren Gewinde gleiche Steigung besitzen müßten und
welche durch Verdrehen eine gleichmäßige Annäherung oder Entfernung der
Hebeldrehpunkte bewirkte, mit Vortheil verwenden.
Tafeln