| Titel: | Krauss'sche Kuppelung. |
| Fundstelle: | Band 215, Jahrgang 1875, S. 398 |
| Download: | XML |
Krauss'sche Kuppelung.
Mit Abbildungen auf Taf.
X [a/4].
Krauß'sche Kuppelung.
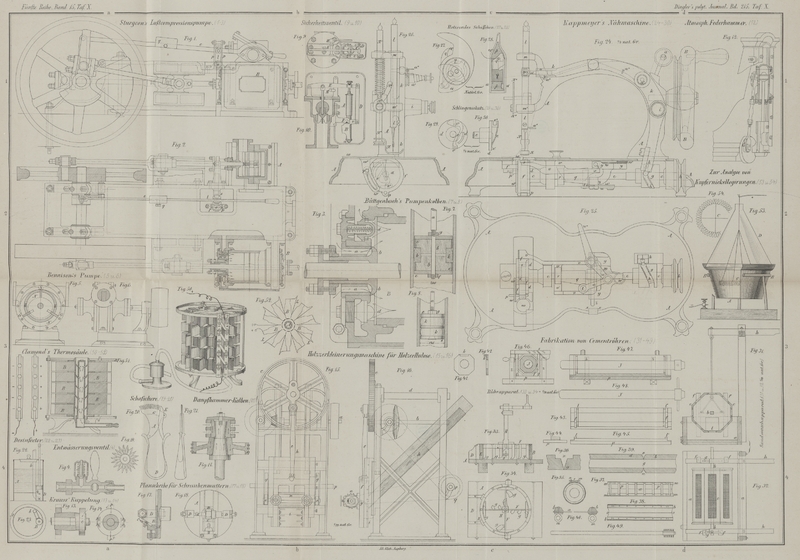
Vorliegende in Figur
13 und 14 skizzirte Kuppelung ist bereits in diesem Journale (1865 177 458) und zwar unter dem Namen „Dehessele'sche Kuppelung“ aufgeführt
worden. Die zweitheilige Kuppelung besteht bekanntlich aus schwach conischen Schalen
a, b, welche durch zwei aufgezogene schmiedeiserne
Ringe gegenseitig und mit den stumpf zusammenstoßenden Wellenenden verbunden
werden.
Gelegentlich eines Vortrages im bayerischen Industrie- und Gewerbeverein
(vergl. dessen Blatt, 1875 S. 59 und 63) wurde nun von Director Krauß in München constatirt, daß er diese Wellenkuppelung
bereits im J. 1859 bei Errichtung der Werkstätten der Schweizer Nordostbahn in
Zürich entworfen und angewendet habe, daher die Priorität der Erfindung gegenüber
Dehessele wohl beanspruchen könne, ohne damit
auszuschließen, daß dieser ganz unabhängig auf die Kuppelung gekommen sei. Professor
Ludewig erwähnt bei dieser Gelegenheit, daß die beiden
Kuppelungsringe mit schrägen Vorsprüngen c versehen
werden könnten, wodurch Schläge mit dem Hammer eine Drehbewegung und ein Auftreiben
der Ringe nach einer schwachen Schraubenlinie bewirken. Diese Vorsprünge müßten
durch Blechringe verdeckt werden, um Unfälle zu vermeiden.
Durch eine einfache Rechnung zeigte noch der Vortragende, daß sich seine Kuppelung
für jede Größe der zu übertragenden Kraft eigne.
Es sei p die Kraft, mit der jede der
beiden Kuppelschalen durch den conischen Ring an die Welle angepreßt werden muß, um
die Reibung R zu erzeugen, welche der zu übertragenden
Kraft der Welle von einem gegebenen Durchmesser d
entspricht. Bezeichnet f = 0,2 den Reibungscoefficient,
so ist die Größe dieser Reibung dargestellt durch R = 2
pf.
Dieselbe wirkt an der Peripherie der Welle; das Moment derselben
R(d/2) gleichgesetzt dem
Torsionsmoment, welches die Uebertragungsfähigkeit der Welle repräsentirt,
R(d/2) = 2 pf (d/2) = (π/16) d³ S
gibt
pf = (π/16) d²
S (1)
Nimmt man zur Berechnung der Dimensionen des Ringes an, die Kraft
p/2 suche den Ringquerschnitt q zu zerreißen, so erhält man
p/2 = qS
(2)
Setzt man die Spannung S des Ringes gleich derjenigen der Welle
und combinirt die beiden Gleichungen (1) und (2), so erhält man unter Elimination
von p zur Berechnung des Ringquerschnittes:
q = (π/32) (d²/f).
Für eine Welle von 60 Mm. Durchmesser ergibt sich nach dieser
Formel ein Ringquerschnitt von
q = (π/32)
(60²/0,2) = 1800 Quadratmillim.
Dabei ist der Voraussetzung gemäß angenommen, daß Welle und Ring
gleich stark beansprucht sind.
Tafeln