| Titel: | Ueber die Beziehungen von Stoss und Druck in ihrem Gebrauche zu Deformationsarbeiten; von Friedrich Kick, Professor am deutschen Polytechnicum in Prag. |
| Autor: | Friedrich Kick [GND] |
| Fundstelle: | Band 216, Jahrgang 1875, Nr. , S. 377 |
| Download: | XML |
Ueber die Beziehungen von Stoss und Druck in
ihrem Gebrauche zu Deformationsarbeiten; von Friedrich Kick, Professor am deutschen Polytechnicum
in Prag.
Mit Abbildungen auf Taf.
VIII [a.b/1].
Kick, über die Beziehungen von Stoß und Druck in ihrem Gebrauche zu
Deformationsarbeiten.
Die Technologie kennt eine große Zahl von Formänderungen der Materialien, welche bald
durch ruhig oder stetig wirkende Kräfte, bald durch Stöße herbeigeführt werden. Wir
erinnern hier an das Schmieden mittels Hammerarbeit und, im Gegensatze hierzu, an
Haswell's Preßschmieden; an das Prägen unter den
alten Fall- und Prägwerken und unter der Uhlhorn'schen Maschine oder unter hydraulischen Pressen; an die
Stabeisenfabrikation in den alten „Eisenhämmern“ und an jene in
den modernen Walzwerken; an die Nietenfabrikation durch Schmieden und jene durch
Pressen; an das Steinbohren durch Meißelbohrer und jenes durch den rotirenden
Diamantbohrer u. a. m.
Ein Blick auf die hier bezogenen Beispiele zeigt, daß jene Mittel, welche durch Stoß
wirken, einer weit älteren Zeit entsprangen und unstreitig auch constructiv
einfacher sind als jene, wobei ruhiger, entsprechend angewendeter Druck dieselbe und
oft noch bessere Arbeit vortheilhafter verrichtet.
Es ist auch nicht zu gewagt, den Schluß zu ziehen, daß die Technik der Neuzeit sich
bestrebt, stoßend wirkende mechanische Mittel durch drückend wirkende zu
ersetzen.
Gebrauchen wir das Wort Druck der Kürze wegen für ruhig
und stetig wirkende Kräfte, mögen dieselben das Material auf Zug-,
Druck-, Schub-, Biegungs- oder Torsionsfestigkeit in Anspruch
nehmen, sei uns also dieses Wort im Folgenden ein bequemer Ersatz für
„ruhige Inanspruchnahme“ im Gegensatz zum Stoß, so können
wir sagen: Es zeigen die vorerwähnten Beispiele, daß stoßend wirkende mechanische
Mittel mit Erfolg durch drückend wirkende ersetzt werden können, und dies legt den
weiteren Schluß nahe, daß der Arbeitsaufwand für Deformationen
unter ruhigem Drucke kleiner sei, als jener bei Anwendung von Stößen.
Zu diesem Satze, dessen Richtigkeit in seiner vollsten Allgemeinheit — d. h.
mit Beziehung auf beliebige Zahl und Intensität der Stöße und für jedes Material
— wir behaupten, gelangten wir durch anderweitige Betrachtungen, und sei er
zunächst durch solche seiner scheinbaren Ungereimtheit, des scheinbaren
Widerspruches mit den Erfahrungen des täglichen Lebens entkleidet.
Jede Deformationsarbeit (sei dieselbe ein Dehnen, Verkürzen, Biegen, Reißen, Brechen
etc.) läuft daraus hinaus, die kleinsten Theilchen eines Körpers, oder wenigstens
jene eines Theiles des Körpers, in eine andere relative Lage zu bringen. Jeder
Verschiebung der kleinsten Theilchen, welche bei einer Deformation ihre gegenseitige
relative Lage ändern müssen, wird durch die „inneren“ Kräfte
ein gewisser Widerstand entgegengesetzt. Denken wir uns nun ganz dieselbe
Deformation einmal durch einen ruhigen Druck, ein zweites Mal durch einen Schlag
hervorgebracht, so sind die inneren Widerstände durch die gleichen Wege überwunden
worden und beide Arbeitsgrößen müßten daher gleich sein,
d. h. die mechanische Arbeit (Kraft mal Weg) des durch ruhige Inanspruchnahme
(Druck) wirkenden, entsprechend construirten Apparates müßte gleich der Stoßarbeit
oder der zur Deformation verwendeten lebendigen Kraft des stoßend wirkenden
Werkzeuges sein.
Dieser ideelen Forderung kann aber nicht entsprochen werden; der Stoß muß immer
Verdichtungen der unmittelbar stoßenden und gestoßenen Oberfläche und Vibrationen
zur Folge haben, welche mit der praktisch beabsichtigten Formänderung Nichts zu thun
haben, und hierfür geht ein guter Theil von mechanischer
Arbeit verloren. Läßt man z. B. auf einen an seinen beiden Enden unterstützten
Eisenstab ein Gewicht in der Mitte des Stabes auffallen, so wird nicht allein eine
bestimmte Durchbiegung die Folge sein, sondern auch eine Compression der unmittelbar
durch den Schlag getroffenen äußeren Schichten und in Consequenz hiervon eine oft
sehr beträchtliche Erwärmung. Das mechanische Aequivalent einer Wärmeeinheit ist
aber bekanntlich 424mk; es geht daher bei verhältnißmäßig geringer Erwärmung einer größeren
Masse, in Folge der Verdichtung durch Stöße, ein bedeutender Theil der Stoßarbeit
für Formveränderung verloren. Hierzu gesellen sich noch die Vibrationen der
Unterlage.
Dies wird man zugeben, doch behaupten, daß der Stoß vortreffliche Dienste leistet,
wenn ein starrer Körper getheilt werden soll. Man wird sagen: „Das
Zersprengen eines Steinblockes vermittels mehrerer Eisenkeile, die in eine in
den Stein gemeißelte, geradlinige Furche gesetzt und dann mit mäßig starken
Schlägen angetrieben werden, erfordert eine ungemein kleine
Wirkungsgröße, wenn man sie mit jener vergleicht, die erforderlich wäre, um den
Stein durch eine nur durch Druck wirkende Belastung zu zerbrechen. Dies erklärt
sich dadurch, daß beim Zersprengen mit Keilen nur allein jene Körpertheilchen,
welche in der Sprungfläche liegen, erschüttert zu werden brauchen, um eine
Trennung derselben zu bewirken, während die ganze übrige Masse des Steinblockes
unverändert bleiben kann; wo hingegen, wenn ein Zerbrechen durch Belastung
hervorgebracht werden soll, in allen Theilen der Steinmasse Ausdehnungen oder
Zusammenpressungen hervorgebracht werden müssen, von denen nur diejenigen,
welche in der Nähe der Brechungsebene stattfinden, zweckdienlich sind. Der
Vortheil des Zersprengens beruht also darauf, daß eine gewisse lebendige Kraft
gerade nur auf diejenigen Körpertheile wirksam gemacht wird, die von einander
getrennt werden sollen, wo hingegen beim Zerbrechen durch Druck der ganze Körper
unnöthiger Weise deformirt wird.“Redtenbacher: Principien der
Mechanik.
Dem Satze: Der Vortheil des Zersprengens beruht darauf, daß eine gewisse Arbeit
gerade nur auf diejenigen Körpertheile wirksam gemacht wird, die von einander
getrennt werden sollen, stimmen wir vollkommen bei; dies kann aber auch ohne
Anwendung von Stößen geschehen. Wir erinnern an das Sprengen von Steinen durch
befeuchtete Holzklötze; auf das Zerklüften durch die Wirkung gefrierenden Wassers
und an das Absprengen von Glas durch entsprechende Erwärmung und plötzliche
Abkühlung. Wird durch diese Mittel nicht auch ein Sprengen erzielt, mit geringem
Arbeitsaufwande und doch ohne Schlag? Ja noch mehr. Wir kennen seit einigen Jahren
in vielen Haushaltungen ein einfaches Werkzeug zum Zerkleinern des Zuckers, die
sogen. Zuckerzange, welche das „Zuckerschlagen“ mit Messer und
Hammer — vergleichbar dem Keil und Schlägel der Steinmetze —
verdrängte. Wer dieses einfache Werkzeug nicht zu handhaben versteht, wird wohl beim
alten Verkleinerungsverfahren bleiben; wer jedoch einige Fertigkeit erlangte, wird
gewiß gefunden haben, daß der Zweck mit weniger Anstrengung (Arbeit) erreicht wird.
Unseres Wissens ist dies (von den meist irrationellen Schotterquetschen abgesehen)
das erste Zerkleinerungswerkzeug für einen starren Körper, welches auf ruhigem Druck
basirt; doch zweifeln wir nicht, daß weitere folgen werden.
Redtenbacher sagt ferner: „Das Eintreiben eines
Pfahles in die Erde ohne Anwendung von Schlägen ist so zu sagen eine praktische
Unmöglichkeit. Wollte man einen Pfahl auf irgend eine Weise in die Erde hineindrücken, so
würden dazu ganz riesenmäßige Vorkehrungen und Veranstaltungen nothwendig
werden; man müßte entweder auf den Pfahl eine Last legen, die ungefähr dem
Gewicht eines Hausbaues gleich käme, oder man müßte, wenn man das Eintreiben
mittels einer Presse bewerkstelligen wollte, diese Presse zuerst mit dem
Erdboden so stark befestigen, wie es der Pfahl ist, wenn er einmal in der Erde
steckt; dabei setzt man also voraus, daß das, was erst entstehen soll, bereits
vorhanden sei.“
Es ist auch hier, der „nützlichen Wirkung der Schläge“ zu liebe,
zu weit gegangen worden.
Ganz abgesehen davon, daß das Einschrauben von Piloten in das Erdreich oft möglich
und auch vortheilhaft sein kann, ist so viel gewiß, daß die Kraft oder der Druck,
welcher zum Eintreiben erforderlich wäre, nichts weniger als exorbitant zu nennen
ist.
Denken wir uns die Hauptmauer eines vierstöckigen Gebäudes auf einer einfachen
Pilotenreihe ruhend und sei der Abstand der Piloten, Mittel zu Mittel, 3 Fuß, so ist
die Belastung eines Pfahles ca. 500 Ctr. (oder 25 000k), wobei die Mauerstärken des
Keller- und Erdgeschosses zu je 3, der drei Stockwerke zu 2, 2
beziehungsweise 1½ Fuß angenommen würden. Man wird gewiß nicht behaupten
können, daß ein Druck von 500 Ctr. nicht mehr zu erzielen ist. Denken wir uns das
Pilotirungsschiff, oder bei Landpilotirungen einen Wagen, mit dieser Last beladen,
so kann die auf diesem Vehikel entsprechend angebrachte Presse den geforderten Druck
ausüben. Ja selbst wenn doppelte und dreifache Sicherheit verlangt wäre, d. h. wenn
man forderte, daß die Pilote selbst bei 1000 oder 1500 Ctr. nicht mehr weiter
einsinken darf, so würde auch die Erzielung dieses Druckes auf keine
unüberwindlichen Schwierigkeiten stoßen.
In lockeren Boden (Sandboden) hat Capt. Liernur, und nach
ihm Andere, das Eintreiben der Piloten mit ausgezeichnetem Erfolge dadurch erzielt,
daß er längs der Pilote ein Röhrchen anbrachte, dessen Oeffnung nahe der
Pilotenspitze einen dünnen aber kräftigen Wasserstrahl austreten ließ, wodurch der
feine Sand zur Seite geschafft und gegen oben verdrängt, das Niedersinken der Pilote
gestattete. Es liefert dieses Verfahren ebensowohl einen Gewinn an Zeit, als an
mechanischer Arbeit.
Mit diesen Betrachtungen soll nur gezeigt werden, daß der Vortheil der Anwendung der
Ramme zum Pilotiren, oder allgemeiner gesprochen, der Anwendung von Stößen ein sehr
fraglicher ist.
Es kommt wohl — z. B. bei Montirungen — vor, daß man einen schweren
Körper durch Schläge verschiebt, resp. in die richtige Position bringt, und es wird dieses
Mittel seiner Einfachheit wegen auch immer hier und da Verwendung finden; in diesen
Fällen ist sich aber der Mechaniker klar, daß Arbeit für die Bewegung verloren geht
(d. h. in Disgregation und Wärme verwandelt wird) und daß Hebel, Winden und dergl.,
wo sie anwendbar sind, vortheilhafter wirken.
So wie nun Stöße zum Zwecke von Massenbewegungen einen Verlust an Arbeit bedingen
— und zwar darum, weil ein Theil der im stoßenden Körper angesammelten Arbeit
als Disgregations- und Wärmearbeit verloren geht, — so bedingen auch
Stöße, zu Formänderungen oder Deformationen angewendet, stets einen Verlust an
Arbeit, weil sich Compressionen der äußersten Schichten, und Umsetzung von Arbeit in
Wärme in einem größeren Maße als bei Anwendung ruhigen Druckes nicht vermeiden
lassen.
Es kann behauptet werden, daß sich die Wirkung von Stößen mit der Wirkung stetiger
Kräfte (Drücke) überhaupt nicht vergleichen lasse, indem die Deformationen ganz
andere sind. Dies geben wir für viele Fälle ohneweiters zu, ja wir werden hierauf in
einer späteren Arbeit zurückkommen; doch kann in anderen und sehr zahlreichen
Fällen, z. B. dem Durchbiegen einer Achse, dem Prägen einer Münze u. s. w., ganz
wohl gefragt werden, wie sich die Arbeitsgrößen verhalten für dieselbe Durchbiegung,
dieselbe Prägung u. s. w., wenn Stöße oder wenn Druck zur Formänderung angewendet
wurde. Für solche Fälle haben wir behauptet, daß ganz allgemein der Arbeitsaufwand
für dieselbe Deformation unter Anwendung von Druck kleiner sei, als unter Anwendung
von Stoß.
Wir wollen unsere Behauptung durch eine Reihe von Versuchsergebnissen belegen, welche
wir theilweise der Literatur entnehmen.
I. In einem Vortrage über Stahlbronze, gehalten am 10.
April 1874 (im Selbstverlage gedruckt), veröffentlicht General Franz Ritter v. Uchatius Resultate über Zerreißversuche von Geschützgußeisen durch Stoß
und Zug.
Die Länge des Stäbchens betrug 75mm, der Querschnitt 0qc,5, das Fallgewicht 1k,15.
m
mk
Die Stäbchen rissen bei
0,72
Fallhöhe beim
1.
Stoße, entspricht
0,828
Die Stäbchen rissen bei
0,63
Fallhöhe beim
2.
Stoße, entspricht
1,43
Die Stäbchen rissen bei
0,54
Fallhöhe beim
4.
Stoße, entspricht
2,48
Die Stäbchen rissen bei
0,45
Fallhöhe beim
8.
Stoße, entspricht
4,14
Die Stäbchen rissen bei
0,36
Fallhöhe beim
14.
Stoße, entspricht
5,80
Die Stäbchen rissen bei
0,27
Fallhöhe beim
37.
Stoße, entspricht
11,49
Die Stäbchen rissen bei
0,18
Fallhöhe beim
352.
Stoße, entspricht
72,86
Die Stäbchen rissen bei
0,09
Fallhöhe beim
2052.
Stoße, entspricht
212,38
Es wurde mithin mit dem geringsten Arbeitsaufwande das Reißen bei einer Fallhöhe von
0m,72 bewirkt und
betrug derselbe 0mk,828. Es könnte angenommen werden, daß eine zwischen 0m,63 und 0m,72 liegende Fallhöhe
bereits für das Zerreißen hingereicht hätte; da aber bei 0m,63 bereis zwei Schläge erforderlich
waren, der Arbeitsaufwand für einen Schlag hier 0mk,715 beträgt, so kann die Zahl 0,828
als dem Minimum der zum Zerreißen erforderlichen Stoßarbeit sehr naheliegend
betrachtet werden.
Man erreicht also eine Deformation durch Stöße(oder
Schläge) mit um so kleinerem Arbeitsaufwande, je weniger und
je kräftigere Stöße man hierzu verwendet.
Fragen wir nun nach dem Arbeitsaufwande, welcher für dasselbe Material bei ruhigem
Drucke (Zuge) zum Zerreißen erforderlich war. Die Versuche ergaben:
Textabbildung Bd. 216, S. 382
Last in k pro 1qc Querschnitt; Dehnung in 0,00001
der Länge; elast; bleib; Last in k pro 1qc Querschnitt; Dehnung in 0,00001 der Länge; elast;
bleib.
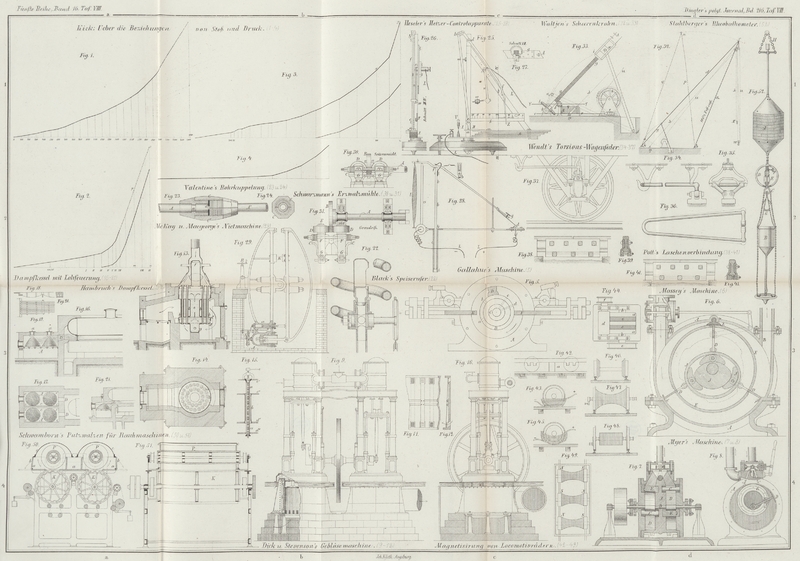
Nach diesen von General Uchatius gegebenen Versuchsdaten
ist das Arbeitsdiagramm Fig. 1 construirt, wobei
die Abscissen die Gewichte (100k als ½cm) und die Ordinaten die totale Dehnung, d. h. den Weg der Kraft
(1/1000 der Länge d. i. 75/1000mm als 2cm) darstellen.
Dieses Diagramm liefert als Arbeitsaufwand für das Zerreißen eines Stäbchens von
1qc
Querschnitt aus Geschützgußeisen nahe 0mk,2, daher für
½qc Querschnitt aus Geschützgußeisen nahe 0mk,1.
Vergleichen wir diese Zahl mit dem Arbeitsaufwande 0mk,828 für das Zerreißen durch Stoß, so
stellt sich die Stoßarbeit als achtmal größer als die
Druckarbeit dar.
Die Arbeit für die Dehnung bis zur Elasticitätsgrenze beträgt, bei ½qc Querschnitt, etwa
0mk,003; es würde
dies einem Schlage des Gewichtes pr. 1k,15 von weniger als 3mm Fallhöhe entsprechen, während Uchatius fand, daß schon bei 30mm die Schläge dieses Gewichtes die
Elasticitätsgrenze nicht übersteigen.
Wenn die erst angegebene Versuchszahlenreihe nachweist, daß ein kräftiger Schlag eine
günstigere Ausnützung der lebendigen Kraft liefert wie mehrere schwächere Schläge,
und hierauf gezeigt wird, daß dieselbe Wirkung durch ruhige Inanspruchnahme mit
einem geringeren Arbeitsaufwande erzielt wird, als bei dem einen Schlage, so folgt ganz allgemein, daß zur gleichen Deformation
Schläge einen größeren Arbeitsaufwand erheischen als ruhige Inanspruchnahme, für
welche wir das Wort „Druck“ gebrauchten. Durch diese Versuche
ist also obige Behauptung für Gußeisen bestätigt.
II. Hr. Robert Lane Haswell
machte zwei comparative Versuche,Wir sprechen für die Mittheilung dieser Versuche, welche noch nicht publicirt
wurden, unseren Dank aus. eine und dieselbe Achse durch ruhigen
Druck zu biegen und hierauf durch Schläge wieder gerade zu richten. Ist eine
bleibende Durchbiegung nicht sehr bedeutend, so kann der Arbeitsaufwand, welcher für
das Geraderichten erforderlich ist, gleich dem Arbeitsaufwand für die Biegung
genommen werden; denn derselbe Stoß (Fallklotzgewicht mal Hubhöhe), welcher eine
gewisse Biegung erzielte, richtet, in gehöriger Weise ausgeübt, das gebogene Stück
auch wieder gerade. Dies vorausgeschickt, lassen Haswell's Versuche jenen Vergleich zu, welchen unsere Behauptung
erfordert.
Bei der angewendeten Hebelpresse betrug das auf das Hebelende reducirte Hebel-
und Schalengewicht zusammen 241k,25; der kurze Hebelarm hatte 210mm, der lange 4845mm, und war daher das
Uebersetzungsverhältniß 23,07. Der Abstand der Auflagen betrug 1m,5. Die Druckprobe
ergab bei einer Schmiedeisen-Achse von 132mm,75 Durchmesser nachstehende
Resultate.
Textabbildung Bd. 216, S. 383
Auflage auf der Waageschale;
Durchbiegung; elast; bleib; Anmerkung; k; mm; mm; Die
Auflagegewichte sind um obengenannte 241k,25 zu vermehren und diese Summen je
mit 23,07 zu multipliciren, um die in der Mitte der Achse ausgeübten Drücke zu
finden.
Diesen Daten entsprechend ist in Fig. 2 das Arbeitsdiagramm
gezeichnet, welches für die bleibende Durchbiegung von 24mm den Arbeitsaufwand von 125mk liefert, und zwar
entsprechen die Ordinaten wieder den Dehnungen (3mm für 1mm Durchbiegung) und die Abscissen den
Belastungen, welche aber erst in der Umrechnung auf das Uebersetzungsverhältniß von
23,07 reducirt wurden; in dem Diagramm ist 1mm = 10k genommen, entspricht also thatsächlich
230k,7. —
Da die Daten bezüglich der elastischen Streckung für die beiden letzten Belastungen
nicht angegeben sind, so wurde das Diagramm nach dem Gefühle ergänzt; der hierdurch
mögliche Fehler kann das Resultat um höchstens 10mk beeinträchtigen.
Dieselbe Achse wurde nun durch Schläge unter einem Fallwerk zurückgebogen.
Schlag
Fallhöhe
Durchbiegung
m
mm
1
0,600
12
2
0,600
5
3
0,332
3
4
0,335
– 2
Indem das Gewicht des Fallklotzes 649k,5 betrug, so beläuft sich der gesammte
Arbeitsaufwand für das Zurückbiegen (eigentlich wurde eine kleine Krümmung nach der
entgegengesetzten Seite erhalten) auf 1212mk,6. — Blos für das Zurückbiegen
um 12mm wurden 389mk,7 aufgewendet.
Unser Diagramm weist für die Arbeit der Biegung von 12 bis 24mm bleibender Deformation in der
Fläche mnop den Arbeitsaufwand von ca. 56mk auf; es verhält
sich demnach hier die Druckzur Stoßarbeit wie 56: 389,7
oder nahe 1 zu 7.
Weil aber bei den wiederholten und schwächeren Schlägen der Arbeitsaufwand, wie dies
auch Uchatius fand, noch größer wird, so kann es nicht
Wunder nehmen, daß die gesammte Druckarbeit von 125mk zur gesammten Schlagarbeit von 1212mk,6 sich nahe wie
1:10 verhält.
Einen zweiten Versuch machte Haswell mit einer Bessemerstahlachse von 129mm,5 Durchmesser.
Dieselbe wurde durch ruhigen Druck auf eine bleibende Durchbiegung von 12mm,5 gebracht, und
hierzu die oberwähnte Hebelpresse verwendet.
Die Versuchsdaten sind folgende.
Textabbildung Bd. 216, S. 385
Auflage auf der Waageschale;
Durchbiegung; elast; bleibend; Auflage auf der Waageschale; Durchbiegung;
elastisch; bleibend
Das auf Grundlage dieser Daten construirte Arbeitsdiagramm Fig. 3 erweist den
Arbeitsaufwand zu etwa 229mk. Bei der Zurückbiegung derselben Achse, durch Schläge unter
dem Fallwerke, wurden nachstehende Resultate erhalten.
Schlag
Fallhöhe
Durchbiegung
m
mm
1
0,6
7,0
2
0,7
2,5
3
0,6
0
Dieser Arbeitsaufwand beträgt 649,5 × 1,9 = 1234mk.
Bei ruhigem Druck beträgt die Biegungsarbeit von 7 bis 12mm,5 (entsprechend Fläche wxyz) 75mk, während der erste
Schlag einer Arbeit von 389mk,7 entspricht. In diesem Falle verhält sich die Druckarbeit zur Stoßarbeit wie 1:5.
III. Bessemerstahlschienen-Proben vom Maschineninspectorate der
indischen Staatsbahn, publicirt im Engineering deutsche
Ausgabe 1. Bd. S. 26 (jetzt Stummer's Ingenieur).
Textabbildung Bd. 216, S. 385
Druckprobe; Schlagprobe. Fallklotz 10 Ctr.
Fallhöhe 5 Fuß; Tonnen; Durchbiegung in Zoll; gesammte; bleibende; Schlag;
bleibende Durchbiegung; Zoll; Bruch.
Der Abstand der Auflagen betrug in beiden Fällen 3 Fuß engl. Die Arbeit für die
bleibende Biegung auf 1,31 Zoll stellt sich nach dem Diagramme Fig. 4 auf ca. 480
Fußpfund, und die Arbeit des ersten Schlages, welcher eine Durchbiegung von 1,25
Zoll hervorbrachte, auf 5000 Fußpfund, mithin verhält sich die Druck- zur Schlagarbeit nahe wie
1:10.
Bei einer zweiten Schiene sind die Versuchsergebnisse:
Textabbildung Bd. 216, S. 386
Druckprobe; Schlagprobe; Tonnen;
Durchbiegung in Zoll; gesammte; bleibende; Schlag; bleibende Durchbiegung;
Zoll.
Der Abstand der Auflagen, die Fallhöhe und das Fallgewicht sind wie oben.
Vergleichen wir die Arbeit des ersten Schlages, welche eine Durchbiegung von 1,19
Zoll hervorbrachte, mit der Arbeit, welche zu derselben Durchbiegung bei ruhigem
Druck erforderlich war, so finden wir das Verhältniß von 5000:420. Die Zahl 420 ist
aus einem Diagramm abgeleitet, welches wir hier weglassen. Die Druckarbeit zur Stoßarbeit stellt sich wie 1:12.
Ganz ähnlich stellt sich dieses Verhältniß bei den Proben der in genannter Quelle mit
Nr. 4, 5 und 10 bezeichneten Schienen, bei welchen wir auch die Vergleichrechnung
durchführten.
Unter den Proben befinden sich auch solche, welche mit gehärteten Schienen vorgenommen wurden, und sind die Versuchsdaten z. B.
bei Schiene Nr. 20 nachstehende.
Textabbildung Bd. 216, S. 386
Druckprobe; Schlagprobe; Tonnen;
Durchbiegung in Zoll; gesammte; bleibende; Schlag; Durchbiegung Zoll; Hierbei
betrug die Fallhöhe 5 Fuß, das Gewicht 6 Ctr.
Aus einem Diagramme bestimmte sich die Arbeit für die Durchbiegung von 0,56 Zoll zu
240 Fußpfund, während der erste Schlag einer Arbeit von 3000 Fußpfund entspricht.
Das Verhältniß der Druckzur Schlagarbeit beträgt
demnach 1:12.
IV. Wir legten eine parallelopipedische Fichtenholz leiste von den Querschnittsdimensionen 13,7
und 19mm hochkantig
auf 0m,6 entfernte
Unterlagen. Durch ruhigen Druck bei einem Arbeitsaufwande (nach einem Diagramm
bestimmt) von ca. 0mk,3 erfolgte der Bruch. Im Schlagwerk wurde der 3k,43 wiegende Hojer durch 0m,1 Höhe fallen
gelassen, ohne daß eine gleiche Leiste brach. Es wurde der Bruch erst bei einer
Fallhöhe von 0m,21
erzielt, was einer Arbeit von 0mk,72 entspricht. Hier verhält sich also die Druckarbeit zur Schlagarbeit für den Bruch wie 1:2,4.
V. Ein Glasstab von 6mm Durchmesser wurde
an einem Ende zwischen Bleibacken im Schraubstock eingespannt, an dem anderen Ende,
im Abstände von 17mm
eine Waageschale im Gewichte von 235g aufgehängt.
Es betrug bei der Belastung von
0k,235
die Biegung 2mm
Es betrug bei der Belastung von
0,435
die Biegung 3
Es betrug bei der Belastung von
0,735
die Biegung 4
Es betrug bei der Belastung von
0,985
die Biegung 5
bei der Belastung von
1,135
erfolgte der Bruch.
Das Diagramm liefert als Brucharbeit näherungsweise 0,34
Kilogramm-Centimeter.
Fallproben.
20g
durch 10cm
Höhe auf das
Ende des Stängelchens fallen gelassen, entsprechend
einer Arbeit von 0,2 Kilogrm.-Centim., kein Bruch,
50g
durch 10cm
Höhe, entsprech.
einer Arbeit von 0,5 Kilogrm.-Centim., kein Bruch,
100g
durch 10cm
Höhe, entsprech.
einer Arbeit von 1,0 Kilogrm.-Centim., erfolgte der Bruch.
Es ist daher auch aus diesem Versuche zu entnehmen, daß für dieselbe
Deformationsarbeit (Bruch) bei Anwendung von Stößen eine größere Arbeitsleistung
erforderlich ist. Es stellt sich die Druckarbeit zur
Stoßarbeit ungefähr wie 1:2.
Es ist, gestützt auf die unter I besprochene
Versuchsreihe, nachgewiesen worden, daß man durch Stöße mit dem geringsten
Arbeitsaufwande eine bestimmte Deformation zu Wege bringt, wenn man nur einen, aber
entsprechend starken Schlag anwendet; es ist ferner dargethan, daß ruhige
Inanspruchnahme ein noch günstigeres Ergebniß bezüglich des Arbeitsverbrauches
liefert und zwar für eine Reihe von Fällen, mit verschiedenen Materialien als
Gußeisen, Schmiedeisen, Stahl, Holz und Glas, und ist somit die Eingangs gemachte
Behauptung durch die Versuche bestätigt worden.
In v. Kaven's
„Collectaneen über einige zum Brücken- und Maschinenbau verwendete
Materialien“ (Hannover 1869) S. 38 ist zwar aus Kirkaldy's Versuchen über plötzlich angebrachte Gewichte das Gegentheil
von dem gefolgert, was wir fanden; wir bemühten uns aber vergebens, die Begründung
für diese gegentheilige Behauptung in jener Schrift zu entdecken. Zudem erscheint
uns die Eingangs gemachte Reflection so wenig anfechtbar, daß diese wohl schon
allein zur aufgestellten Behauptung berechtigt. Man könnte fragen, wie es komme, daß
die Verhältnisse zwischen der Arbeit bei ruhiger Inanspruchnahme und bei Stößen
zwischen 1:2 und 1:12 schwanken. Die durch die bezogenen Versuche erhaltenen
Verhältnißzahlen müssen um mehr variiren, als dies durch den Charakter der
Materialien bedingt ist, weil sie nicht unter ganz gleichen Verhältnissen
vorgenommen wurden. Je weicher und auch je federnder die Unterlage ist, auf welche
das Probestück aufgelegt wurde, um so weniger wirksam muß der Schlag sein, um so
mehr Arbeit geht für die Formänderung der Unterlage oder für Vibrationen verloren.
Schlägt der Fallklotz nicht unmittelbar auf das Probestück, sondern ist eine
Zwischenlage eingeschaltet, wie bei den Versuchen I, so
beeinträchtigt dies das Resultat ebenfalls. Die bedeutenden Abweichungen selbst bei
demselben Materiale, z. B. Schmiedeisen (vergl. Versuche II mit III), sind dadurch erklärt.
Aus den Diagrammen (vergl. Diagramm Fig. 1 und 2) ist zu ersehen, daß, je
zäher ein Körper ist, umsomehr die Form des Diagrammes von der Dreiecksform
abweicht. Oefter pflegt man den Arbeitsaufwand für den Bruch in der Weise
approximativ zu berechnen, daß man das Zerreißgewicht mit der Dehnung beim Reißen
multiplicirt und dieses Product durch zwei dividirt. In den durch die Diagramme Fig. 2, 3 und 4 dargestellten
Fällen würde die mechanische Arbeit für das Zerreißen auf diesem Wege mehr als
doppelt so groß gefunden werden, als sie nach dem Diagramme ist.
Wir haben oben gesehen, daß bei Holz und Glas der Unterschied der Arbeitsgröße bei
ruhigem Druck und jener für den Schlag, für eine bestimmte Deformation nicht sehr
bedeutend ist. Hiermit stimmen einige Versuche überein, die den Vergleich herstellen
sollten, in welchem Verhältnisse die Arbeitsleistung steht, welche erforderlich ist,
um einen Nagel in Holz einzudrücken und andererseits einzuschlagen. Die
Versuchsergebnisse wiesen einen geringen Unterschied bald zu Gunsten des Druckes
bald des Schlages auf.
Aus unserer Darstellung ergeben sich nachstehende Folgerungen:
1) Wendet man Stöße zur Deformirung oder Zertheilung von Körpern an, so ist hierzu
ein größerer Aufwand von mechanischer Arbeit erforderlich, als wenn man ruhigen
Druck hierzu verwendet.
2) Kennt man die mechanische Arbeit, welche einen Körper bei ruhigem Druck zertheilt
oder bricht, so kann man sicher sein, daß ein Stoß,
welcher diese mechanische Arbeit abzugeben vermag, die Zertheilung oder den Bruch
nicht herbeiführt.
3) Ist die mechanische Arbeit für die vorübergehende Deformirung eines Körpers bis
zur Elasticitätsgrenze bekannt, so werden Stöße, welche dieselbe Arbeit abzugeben
vermögen, den Körper nicht bis zur Elasticitätsgrenze
beanspruchen.
Für den Maschinenbau würde hieraus folgen, daß man trachten soll, stoßend oder
schlagend wirkende Mechanismen durch drückend wirkende zu ersetzen, und daß
Maschinen, wie z. B. der Desintegrator (die Schleudermühle), auf einem irrigen
Principe beruhen.
Tafeln