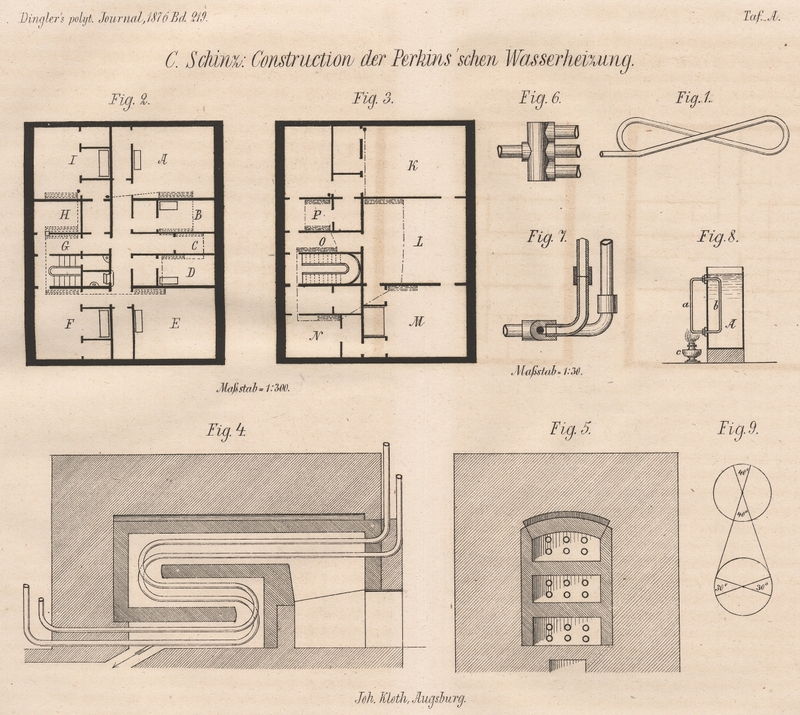
| Titel: | Construction der Perkins'schen Wasserheizung; von C. Schinz. |
| Fundstelle: | Band 219, Jahrgang 1876, S. 439 |
| Download: | XML |
Construction der Perkins'schen Wasserheizung; von C. Schinz.
Mit Abbildungen auf Texttafel A.
(Fortsetzung von S. 340 dieses
Bandes.)
Schinz, über Construction der Perkins'schen
Wasserheizung.
Allgemeine Verhältnisse.Expansionsgefäße.
Der scheinbare Ausdehnungscoefficient des Wassers in eisernen Gefäßen a ist = 0,00033. Nehmen wir als Maximum der Temperatur
des Wassers t'' = 300°, so ist das Volum
ämmtlicher Röhren mit 1 + at'' = 1 + 0,00033 ×
300 = 1,0989 zu multipliciren und das Product von dem ursprünglichen Volum
abzuziehen; der Rest gibt dann das Volum des Wassers an, welches in den Röhren nicht
mehr Platz hat.
Der Inhalt einer Röhre von 100m Länge ist =
100 × 0,000452 = 0cbm,0452. Wenn nun
dieser um 300° erwärmt wird, so bekommt er das Volum 0,0452 × 1,0989 =
0cbm,0497, und dasjenige des aus der
Röhre expulsirten
Wassers ist 0,0497 – 0,0452 = 0cbm,0035. So klein nun auch dieses Volum ist, so muß es doch irgendwo Platz
finden, wenn die Röhre nicht bersten soll; denn die Kraft der Ausdehnung ist eine so
große, daß man sie mit Erfolg da verwenden kann, wo alle übrigen Mittel nicht mehr
ausreichen.
Ein Sicherheitsventil kann auf keine Weise die Expansionsröhre ersetzen, um dem durch
die Ausdehnung expulsirten Wasser Raum zu geben. Wäre die Röhre hinter dem Ventile
voll Wasser, so würde dieses selbst bei großer Belastung alsbald gehoben werden,
wenn das Wasser auch nur ganz wenig erwärmt würde; enthält aber diese Röhre Luft, so
wird zuerst diese ausgetrieben und erst, wenn das Wasser das Ventil erreicht, wird
es unfehlbar gehoben werden; das Wasser mag dann auch irgend welche Temperatur
haben, es kommt alles auf den Inhalt der mit Luft gefüllten Röhre an.
Expansionsröhren sind daher unentbehrlich, und zwar muß der Inhalt derselben dem
Inhalte sämmtlicher Röhren, die mit ihm verbunden sind, proportional sein.
Es sei der innere Durchmesser der Expansionsröhre 0m,08, der Querschnitt also 0qm,0050267, so wird die Länge derselben für
den Inhalt von
100
200
300
500
1000
1500m
Röhren gleich
0,895
1,81
2,67
4,47
8,95
18m,9
sein müssen,
um das bei 300° expulsirte Wasser aufzunehmen; das sind
9 Proc. des Inhaltes der Röhren. Man macht aber die Expansionsröhren hinlänglich
groß, um einem doppelt so großen Volum Raum zu geben, da sie hermetisch verschlossen
sind. Dadurch wird dann die ursprünglich in diesen Röhren enthaltene Luft auf die
Hälfte ihres Volums comprimirt.
Natürlich müssen diese Expansionsgefäße höher als die übrigen Röhren zu stehen
kommen, damit die in denselben enthaltene Luft unter keinen Umständen in diese
gelangen könne. Man kann auch, da es nicht so leicht ist, sehr lange
Expansionsröhren darzustellen, deren mehrere zugleich anbringen.
Würde man verschiedene Systeme von einander trennen und sie nicht verkuppeln, so
würde man natürlich jedes System mit besonderer Expansionsröhre versehen.
Verkupplungen.
Die Verkupplung mehrerer Systeme mit einander hat den Vortheil, daß die Druckhöhe der
einen sich mit der der andern ausgleicht, insofern dieselben ungleich sind; wir
haben sogar bereits gesehen, daß, wenn auch eines der Systeme fast gar keine
Druckhöhe darbietet, dafür ein Ueberschuß eines andern Ersatz bieten kann. Dabei ist jedoch
Bedingung, daß alle gekuppelten Systeme gleiche Initial- und Endtemperaturen
haben müssen, da sonst Unregelmäßigkeiten eintreten würden, die alle Vertheilung der
Transmissionsröhren nach Bedarf der Wärmemengen der zu beheizenden Räume unmöglich
machen. In weitaus den meisten Fällen wird dieser Bedingung leicht entsprochen
werden können. Wenn aber z.B. die Perkins'sche Heizmethode zugleich für Trockenräume
mit hoher Temperatur oder gar zum Erwärmen von Flüssigkeiten mitbenützt werden soll,
so ist dann das System oder die Systeme, welche dazu dienen sollen, zu isoliren, und
wenn die Temperaturdifferenzen groß sein sollten, sogar auch im Ofen durch eine
Scheidewand zu trennen.
Die schon in unserm ersten Projecte zur Anwendung gekommene Trennung der Ofenröhren
in mehrere Stücke, um die Spiralen zu umgehen, wird um so nothwendiger und um so
vortheilhafter sein, als die Systeme selbst größer sind, und unter Umständen sogar
zur Bedingung werden, unter welcher sehr große Systeme Anwendung finden können.
In den Figuren
6 und 7 ist dargestellt, wie solche Kupplungen am leichtesten bewerkstelligt
werden können. Da diese stets außer dem Ofen stattfindet, so würde sogar Gußeisen
dem Drucke vollkommen genügenden Widerstand leisten; nur möchte zu befürchten sein,
daß die Gewinde, in welche die Röhren geschraubt werden, ausbrechen könnten; aber
ich denke, daß hämmerbares Gußeisen entsprechen und dann am wenigsten rosten
würde.
Da große Röhrensysteme stets auch eine große Circulationsgeschwindigkeit verlangen,
so wird auch in dieser Beziehung eine Theilung der Ofenröhre in mehrere Stücke den
Vortheil haben, daß das Wasser sicherer und regelmäßiger die Wärme aus den
Verbrennungsproducten aufnimmt.
Einfluß der Differenzent'' – t' und Größe der Systeme.
Am besten und übersichtlichsten können wir die Verhältnisse betrachten, wenn wir für
irgend eine bedeutende Wärmemenge und für verschiedene Werthe von t'' – t' ausrechnen:
1) die erforderlichen Röhrenlängen, 2) den Widerstand in denselben, 3) die
erforderliche Geschwindigkeit, 4) die danach erforderlichen Druckhöhen, 5) die
diesen zukommenden Fallhöhen und endlich 6) alle diese Werthe für 1, 2, 3 und 4
gleich große Systeme.
Es soll die in einem großen Gebäude zu vertheilende Wärmemenge gleich 150000c sein; dann wäre die Menge für
1
System
=
150000c
3
System
=
50000c
2
„
=
75000
4
„
=
37500.
Die Werthe t'' – t' wollen wir für diese vier Systemengrößen
290–60, 290–100 und 250–60 machen.
Es wird vorausgesetzt, daß die mehrfachen Systeme mit einander gekuppelt werden, so
daß die überschüssige Druckhöhe des einen Systems der ungenügenden einer andern zu
Hilfe kommt. Daher sind dann die Werthe R = Widerstände
gegen die Circulation des Wassers für die Zahl sämmtlicher gekuppelten Systeme in
Rechnung zu bringen, da durch die Kupplung die Druckhöhe aller Systeme ausgeglichen
wird; daher wird dann auch die Geschwindigkeit in allen Systemen gleich und zwar um
so kleiner, als die Zahl der Systeme größer ist.
Wir machen also von den bereits bekannten Formeln Gebrauch:
Länge der Transmissionsröhren = Wärmemenge/W.
Länge der Ofenröhren = Wärmemenge/W°.
Diese Länge der Leitungsröhren müssen wir vor der Hand willkürlich nehmen; wir setzen
für 1 System = 25m, für 2 Systeme = 30m, für 3 Systeme = 35m und für 4 Systeme = 40m. Ebenso müssen wir für die Umbiegungen
eine Annahme machen; wir setzen 1/10 der totalen Röhrenmenge.
1 System
2 Systeme
3 Systeme
4 Systeme
t'' – t' = 290 – 100 = 190
m
m
m
m
Länge der Transmissionsröhren
476
238
158
119
Länge der Ofenröhren
57
28
19
14
Länge d. Leitungsröhren
25
30
35
40
–––––––––––––––––––––––––––––––––––––––––––––
Totale Länge
558
296
212
173
Zur Bestimmung von R
558
592
636
692
Werthe von R
1 + 558+ 58 = 617
1 + 592+ 59 = 652
1 + 636+ 63 = 700
1 + 692+ 69 = 762
Circulationsgeschwindigkeit v
0,485
0,2424
0,1616
0,1212
Druckhöhe P = (v²R)/2g
7,40
1,953
0,932
0,570
Fallhöhen P/(s – s')
99,3
26,2
12,51
7,66
t'' – t' = 290 – 60 = 230Länge der
Transmissionsröhren
554
277
184
138
Länge der Ofenröhren
60
30
20
15
Länge d. Leitungsröhren
25
30
35
40
–––––––––––––––––––––––––––––––––––––––––––––
Totale Länge
639
337
239
193
1 System
2 Systeme
3 Systeme
4 Systeme
m
m
m
m
Zur Bestimmung von R
639
674
717
772
Werthe von R
1 + 639+ 63 = 703
1 + 674+ 67 = 742
1 + 717+ 71 = 789
1 + 772+ 77 = 850
Circulationsgeschwindigkeit v
0,4004
0,2002
0,1335
0,1001
Druckhöhen P = (v²R)/2g
5,75
1,517
0,717
0,434
Fallhöhen P/(s – s')= h
62,60
16,51
7,81
4,73
t'' – t' = 250 – 60 = 190Länge der
Transmissionsröhren
696
353
235
176
Länge der Ofenröhren
57
28
16
14
Länge d. Leitungsröhren
25
30
35
40
–––––––––––––––––––––––––––––––––––––––––––––––––
Totale Länge
778
411
286
230
Zur Bestimmung von R
778
822
858
920
Werthe von R
1 + 778+ 77 = 865
1 + 822+ 82 = 905
1 + 858+ 85 = 944
1 + 920+ 92 = 1013
Circulationsgeschwindigkeit v
0,4848
0,2424
0,1616
0,1212
Druckhöhen P = (v²R)/2g
10,26
2,71
1,257
0,759
Fallhöhen h = P/(s – s')
167,4
35,15
16,29
9,84.
Aus dieser Zusammenstellung ergibt sich nun, daß die Theilung in mehrere Systeme vor
allem die erforderliche Circulationsgeschwindigkeit vermindert und in Folge dessen
auch die Widerstände gegen dieselbe und die erforderliche Fallhöhe; dann daß die
erforderliche Röhrenlänge am größten wird, wenn t''
– t' ungleich klein ist und auf einer niedrigeren
Temperatur liegt; wird hingegen diese erhöht, so wird die Röhrenlänge wieder
kleiner. In Beziehung auf Constructionskosten ist also die Differenz t'' – t' = 290
– 100 am vortheilhaftesten, in Beziehung auf die erforderliche Fallhöhe die
Differenz t'' – t' =
290 – 60.
Man wird also letztere Differenz wählen, sobald die Localität und die nothwendige
Disposition nur geringe Fallhöhen bieten, sowie man in diesem Falle auch genöthigt
sein wird, nur kurze Systeme zu machen.
Auf den Brennstoffconsum haben weder die Werthe t''
– t', noch die Länge der Systeme Einfluß; in
dieser Beziehung kommt alles auf die totale Menge der Wärme an, die im Ofen
empfangen wird. Wenn wie z.B. in diesem Falle diese Menge gleich 150000c ist, so ist das Verhältniß des Consums
zum Nutzeffect = 195230 : 150000; also letzterer = 76,96 Proc.
Bestimmung der Größe der Systeme und
Anordnung derselben.
Um die Länge und Menge der Systeme zu bestimmen, ist zu untersuchen, wie groß die
Druckhöhe bei der durch die Localität gegebenen Fallhöhe sein müsse.
Als erstes Beispiel wollen wir annehmen, die 150000c seien für mehrere große Fabriks-
oder Arbeitssäle bestimmt, die zu ebener Erde liegen und zwar so, daß der Ofen auf
demselben Niveau angebracht werden müsse; ferner daß man das möglichst geringe
Röhrenquantum verwende, daher t'' – t' = 290 – 100 = 190 setzen kann.
Unter solchen Bedingungen kann eine Fallhöhe nur dadurch erhalten werden, daß man die
eine Hälfte der Transmissionsröhren in einiger Höhe über dem Boden, die andere auf
oder in demselben anbringt.
Betrachten wir nun die vorstehenden Rechnungsergebnisse für t'' – t' = 290 – 100, so finden
wir daß 1, 2, 3, 4 Systeme die Fallhöhen 96,9, 26,2, 17,51 und 7,66m erfordern. Da wir aber nicht annehmen
können, daß unsere Säle eine solche Höhe haben, so müssen wir also eine größere Zahl
von Systemen machen. Dagegen können wir in diesem Falle alle Leitungsröhren
entbehren und ebenso die Zahl der Umbiegungen auf ein Minimum bringen, wodurch die
Widerstände gegen die Circulation kleiner werden und folglich auch die
erforderlichen Fallhöhen.
Da nun jedes System aus zwei gleich langen Röhren besteht, von denen die eine oben,
die andere unten liegt, so müssen wir die Röhrenlängen mit in Rechnung ziehen, was
dann die Untersuchung etwas weitläufig macht.
Theilen wir die 476m Transmissionsröhren in
6, 7, 8 und 9 Systeme, so bekommen wir:
79,93 68,0 59,5 und 52,9,
somit haben wir pro Temperaturintervall von 10°, da
t – t dann 19
bietet,
79,33/19 = 4,158 68/19 = 3,579
59,5/19 = 3,1316 52,9/19 = 2m,7842.
Diese müssen wir mit den Werthen C
a der Tabelle II multipliciren und die
Producte addiren, die Summen müssen dann =
150000/6 = 25000 150000/7 =
21429
150000/8 = 18750 150000/9 =
16666
werden; wir erhalten:
für 6 Systeme
für 7 Systeme
obere
untere
obere
untere
Röhre
Röhre
t – t
10 =
2548,0
599,1
1130,3
515,7
20 =
2356,7
1090,2
1293,7
938,4
30 =
2177,5
986,3
1347,5
848,9
45 =
2031,6
892,7
1467,7
768,4
50 =
1875,2
802,1
1614,1
690,4
60 =
1705,2
717,2
1748,7
617,4
70 =
1565,4
637,0
1874,3
548,3
80 =
1435,3
561,3
2028,6
483,1
90 =
1313,1
490,2
2193,2
421,9
95 =
599,1
422,9
515,7
364,0
––––––––––––––––––––––––––––––––––––
17607,1
7199,0
15213,8
6196,5
24806,1
21410,3
für 8 Systeme
für 9 Systeme
obere
untere
obere
untere
t – t
10 =
988,9
451,2
879,2
401,2
20 =
1132,0
821,1
1006,4
730,0
30 =
1179,0
748,2
1048,2
660,4
45 =
1284,2
672,3
1141,8
597,8
50 =
1412,3
604,1
1255,6
537,1
60 =
1530,1
540,2
1360,3
480,3
70 =
1640,0
479,8
1458,1
426,5
80 =
1775,0
422,7
1578,1
375,8
90 =
1919,0
369,2
1706,2
328,2
95 =
451,2
318,5
401,2
383,1
––––––––––––––––––––––––––––––––––––
13311,7
5427,3
11835,1
4820,4
18739,0
16655,5
Um nun daraus die Temperatur des Wassers in der Röhre an der Stelle zu bestimmen, wo
diese nach unten umbiegt, reduciren wir die Summen:
17607,1 15213,8 13311,7
11835,1 durch Division
durch die Röhrenlängen
4,158
3,579
3,1316
2,7842 auf
4234,5
4250,6
4250,8
4550,8 und setzen diese
in eine Proportion ein mit 4037,8 : 240, der Zahlsumme der
Werthe C
a Tabelle II für t = 240°, und erhalten dann: t =
252°; daher s – s' für 252 – 100 = 0,95548 – 0,89491 = 0,06057.
Nun hat jedes System 8 Umbiegungen im rechten abgerundeten Winkel, wovon 5 auf den
Ofen kommen, da wir keine Leitungsröhren brauchen; es sind daher die Werthe = R, d.h. Widerstände gegen die Circulation des Wassers
für:
6
Systeme
= R =
1 + 553 + (6 × 8)/2
= 558
7
„
1 + 553 + (7 × 8)/2
= 562
8
„
1 + 553 + (8 × 8)/2
= 566
9
„
1 + 553 + (9 × 8)/2
= 570.
Die Geschwindigkeiten sind 1/6, 1/7, 1/8 und 1/9 der Zahl, die wir für 1 System
gefunden, also
v = 0,080833 0,069285 0,060625 0,053888, und führen wir
nun diese Werthe in die Formel P = (v²R)/2g ein, so erhalten wir
P = 0,1859 0,1376 0,1060 0,0844, und dann gibt uns P/(s – s'), die Höhe, um welche die obere Röhre höher liegen
muß als die in oder auf dem Boden. Wir erhalten h =
3,069 2,271 1,751 1m,393.
Es werden also für den vorliegenden Zweck 7 oder 8 Systeme am passendsten sein, da zu
h = 3,069 kaum Platz ist und h = 1,393 zu niedrig wäre, um freien Durchgang unter der suspendirten
Röhre zu gewähren.
Hätten wir hingegen einen mehr langen als hohen Bau mit 150000c zu versehen, in welchem zugleich die Luft
erneuert werden soll, so wäre die Heizkammer in das Kellergeschoß zu verlegen und
derjenige Werth von t'' – t' zu wählen, der am meisten Druckhöhe liefert, also 290 – 60,
damit der Ofen nicht allzutief im Keller eingegraben werden müsse. Eine so mit
Perkins'schen Röhren versehene Heizkammer hat dann den Vortheil, daß die Luftcanäle
sämmtlich senkrecht unter die zu heizenden Räume geführt werden können.
Da ist nun die nothwendige Länge dieser Heizkammer zu berücksichtigen. Es muß die
Länge der Transmissionsröhren eine solche werden, daß, ähnlich wie im vorliegenden
Falle, jedes System aus 2, 4, 6 oder 8 gleich langen Stücken besteht, welche in
umgekehrter Richtung parallel über einander liegen.
Für 150000c ist bei t'' – t' = 290 – 60 die totale
Länge der Transmissionsröhre = 554m. Für 6
Systeme wäre sie also pro System = 554 : 6 = 92m,33, für 8 Systeme = 554 : 8 = 69m,22. Wenn daher die Heizkammer 80m lang werden müßte, so würde dies eine Systemlänge erfordern, die
zwischen diesen beiden Zahlen liegen würde, und wir wären dann genöthigt, eine
Differenz t'' – t' zu
wählen, welche dieser Bedingung entspräche. Um nun aber nicht allzu weitläufig zu
werden, wollen wir
annehmen, unsere Heizkammer bedürfe einer Länge von 69m, was also eine Theilung in 8 Systeme nach
sich zieht, und jedes System wird dann eine Doppelröhre von 34m,5 Länge liefern.
Die Zahl der Umbiegungen ist bei dieser Anordnung = 11 pro System, daher R = 1 + 554 + 1/2 × 8 × 11 = 599. Die
Geschwindigkeit v = 0,4004 : 8 = 0,05005, daher dann
P = (0,05005² ×
599)/2g = 0,0765.
Nun müssen wir noch den Werth von s – s' suchen, um zu erfahren, wie tief die Sohle des Ofens
liegen muß, um die Druckhöhe zu geben. Wenn wir dabei mit gewissenhaftiger
Genauigkeit verfahren wollen, so müssen wir abermals suchen, wie viel Wärmeeinheiten
die obere Röhre transmittirt. Dies habe ich gethan und gefunden, daß das Wasser da,
wo die erste Umbiegung kommt, noch die Temperatur 263 hat. Daraus ist dann die
Temperaturdifferenz an dieser Stelle = 290 – 263 und s – s = 0,89082 – 0,88095 =
0,00987, was dann für 0m,15 Fall eine
Druckhöhe von 0,0014805 gibt, welche wir aber vernachlässigen gegen die kleine
negative Druckhöhe, die wir im Ofen haben. Dagegen wird dann die Differenz an der
Biegung, welche in den Ofen zurückführt, gleich 263 – 60 und s – s = 0,97279
– 0,89082 = 0,08197 und daraus Distanz der Ofensohle von der untern Röhre
P/(s
– s) = 0,0765 : 0,08197 = 0m,934
und Distanz von der Decke = 0,934 + 0,150 = 1m,084, was zu wenig ist, wenn die Ofendecke
eine Dicke von 0m,6 haben soll; aber nichts
hindert uns, die Röhren in der Heizkammer etwas tiefer anzubringen, um dem Ofen
seine natürliche Lage und Höhe geben zu können.
Der Ofen wird also in die Mitte der Heizkammer gestellt, und von den 8 Systemen
laufen vier nach rechts und vier nach links.
Als drittes Beispiel zur Bestimmung der Systemlänge nehmen wir an, das zu beheizende
Gebäude sei ein großes Wohnhaus für viele Wohnungen, die in 4 Stockwerken vertheilt
sind. Um die Vertheilung in den einzelnen Räumen mit mehr Bequemlichkeit vornehmen
zu können, wählen wir die Temperaturdifferenz t''
– t' = 260 – 60, um eine etwas größere
Röhrenlänge zu bekommen, wenn auch dadurch die erforderliche Druckhöhe vermehrt
wird, da es uns bei 4 Stockwerken kaum an Fallhöhe mangeln wird.
Wir wollen versuchen, mit 3 Systemen auszukommen. Dafür gibt uns die oben ausgeführte
Berechnung für verschiedene Werthe von t'' – t' bereits alle Daten, nämlich R = 944, v = 0,1616 und P = 1,257.
Wenn nun der Wärmebedarf in allen 4 Stockwerken gleich groß ist, so muß das erste
System im obersten 4. Stock 3/4 seiner Wärme abgeben und 1/4 kommt auf den 3. Stock.
Das 2. System gibt 2/4 an den 3. Stock ab und 2/4 gehen an den 2. Stock. Das dritte
System gibt 1/4 im 2. Stock ab und 3/4 im 1. Stock.
Wir müssen also bestimmen, mit welchen Temperaturen das Wasser aus jedem Stockwerke
nach unten gelangt. Dazu ist es nun nicht mehr nöthig, die Röhrenlängen zu
berücksichtigen. Jedes System enthält die Summe von 4037c,8; der vierte Theil davon ist 1009c,5.
Der oberste 4. Stock fordert aber 4037,8
– 1009,5
= 3028c,3
aus dem ersten Systeme und
der 3. Stock empfängt
= 1009c,5
aus dem ersten Systeme und
4037,8 – 2 × 1009,5
= 2018c,8
aus dem zweiten Systeme.
Der 2. Stock empfängt
2 × 1009,5
= 2019c,0
aus demselben und
4037,8 – 3 × 1009,5
= 1009c,3
aus dem dritten Systeme.
Der 1. Stock empfängt
4037,8 – 1009,5
= 3028c,3
aus demselben.
Nun haben wir die zu den Wärmemengen 3028,3 2018,8 1009,5 zugehörigen Temperaturen zu
suchen. Die Summen C
a Tabelle II 3176,7 für 220°, 2139,2
für 190° und 943,5 für 140° geben die Proportionen
3176,7 : 3028,3 = 220 : x
x = 209°
2139,2 : 2018,8 = 190 : x
x = 179°
943,5 : 1009,5 = 140 : x
x = 150°.
Nun kennen wir blos die Fallhöhen durch die Stockwerke hindurch und müssen erst
suchen, jene im Kellergeschosse zu bestimmen, um die nothwendige Druckhöhe zu
erhalten.
Das 1. System liefert uns t – t
250 – 209
s – s =
0,91126 – 0,89565 = 0,01561 von Stock 4 nach 3, dann
209 – 60
0,97279 – 0,91126 = 0,06153 von Stock 3 nach Ofen.
Das 2. System liefert uns t – t
250 – 179
0,92302 – 0,89565 = 0,02737 von Stock 3 nach 2, dann
179 – 60
0,97279 – 0,92302 = 0,04977 von Stock 2 nach Ofen.
Das 3. System liefert uns t – t
250 – 150
0,93467 – 0,89565 = 0,03902 von Stock 2 nach 1, dann
150 – 60
0,97279 – 0,93467 = 0,03812 von Stock 1 nach Ofen.
Sind nun die Fallhöhen pro Stockwerk = 3m,1,
so können wir damit einstweilen die Druckhöhen berechnen, welche sich bis auf den
Boden des ersten Stockwerkes ergeben, und wir erhalten:
0,01561 × 3,1 = 0,048391
0,06153 × 6,2 = 0,381486
0,02737 × 3,1 = 0,084847
0,04977 × 3,1 = 0,154287
0,03902 × 3,1 = 0,120962
Die erforderliche Druckhöhe ist
= 1,257000
Davon ab die obenberechnete
= 0,789973
–––––––––
Bleiben noch zu erzeugen
0,467027
Die Summe der Werthe s – s für die drei zum Ofen zurückkehrenden Röhren ist: 0,06153 + 0,04977 +
0,03815 = 0,14942; dividiren wir diesen in der noch zu erzeugenden Druckhöhe, so
erhalten wir 0,467027 : 0,14942 = 3m,125
als nöthige Entfernung der Ofensohle vom Boden des ersten Stockes. Wir hätten
dann:
0,01561 × 3,1
=
0,048391
0,06153 × 9,325
=
0,573760
0,02737 × 3,1
=
0,084847
0,04977 × 6,225
=
0,309820
0,03902 × 3,1
=
0,120962
0,03812 × 3,125
=
0,119130
–––––––––––
1,256960 als erforderliche Druckhöhe.
Das sind freilich andere Verhältnisse als jene Lilliputsysteme von 60 bis 70m für die Transmission von 6000c, welche weder die erwartete Transmission
geben, noch einen Nutzeffect, der höher wäre als jener der geringsten
Heizmethode.
(Schluß folgt.)
Tafeln